[智能算法]可微的神經網絡搜索算法-FBNet

一、概述

? ? ? ? 相較于基于強化學習的NAS，可微NAS能直接使用梯度下降更新模型結構超參數，其中較為有名的算法就是DARTS，其具體做法如下。

? ? ? ? 首先，用戶需要定義一些候選模塊，這些模塊內部結構可以互不相同（如設置不同種類和數量的卷積，使用不同種類的連接結構等）；其次，用戶也需要指定神經網絡的層數，每一層由候選模塊的其中之一構成。

? ? ? ? 由于搜索空間= $Blocks^{layers}$ （其中 $Blokcs$ 為候選模塊種類， $layers$ 為預先指定的神經網絡層數）巨大，為了從龐大的搜索空間中找到合適的結構，需要引入superNet。

二、SuperNet

? ? ? ? 以下內容均基于論文：FBNethttps://openaccess.thecvf.com/content_CVPR_2019/papers/Wu_FBNet_Hardware-Aware_Efficient_ConvNet_Design_via_Differentiable_Neural_Architecture_Search_CVPR_2019_paper.pdf

? ? ? ? 2.1模型結構

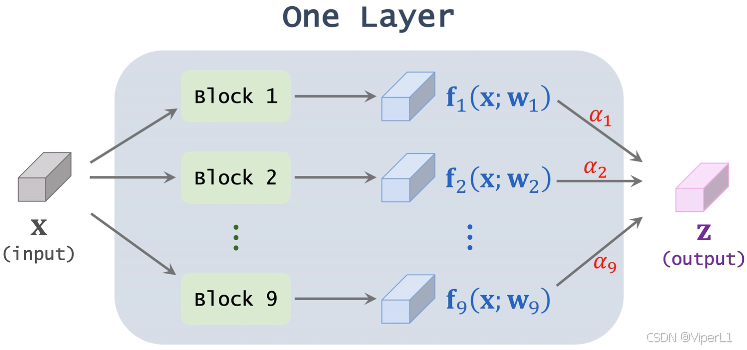
? ? ? ? 這里以SuperNet中的某一層為例，設置候選模塊一共9種，這層superNet由9種不同的模塊并聯而成。輸入向量 $x$ 在候選模塊處理后分別得到9個向量 $f$ ，這個處理過程記作： $y=f_i(x,w_i)$ ，其中 $w_i$ 為模塊中的權重。將這些向量 $f$ 進行加權求和，這些權重記作 $\alpha$ ，所有 $\alpha$ 之和為1（由softmax計算得到），權重 $\alpha$ 就是模型要學習的神經網絡結構超參數。

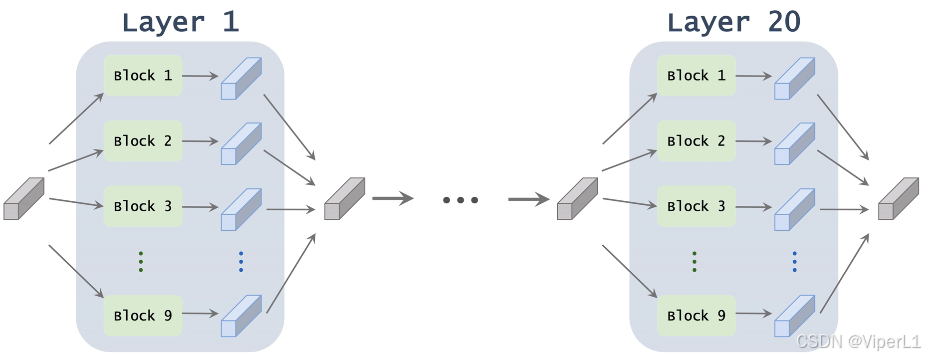
? ? ? ? 通過堆疊上述模塊，組成一個完整的superNet，經過訓練，每一層最終會保留一個模塊。

? ? ? ? 2.2訓練

? ? ? ? 將superNet的候選模塊一共9個，記作 $j=1,...9$ ；設superNet一共20層，記作 $l=1,...20$ ；得第 $l$ 層中第 $j$ 個模塊的參數記作 $w_j^{(l)}$ 和 $\theta_j^{(l)}$ ，故 $W=\{w_j^{(l)}\}_{j,l}$ ， $\Theta=\{\theta_j^{(l)}\}_{j,l}$ ，這兩個即為需要訓練并學習的參數。superNet做出的預測記作 $p(x_i;W,\Theta)$ 。

? ? ? ? 交叉熵損失函數可以寫作 $min_{W,\Theta}\frac{1}{n}\sum_{i=1}^nLoss(y_i,p(x_i;W,\Theta))$ ，在這個損失函數中，由于 $p$ 是關于 $\Theta$ 的函數，且兩者可微，故損失函數 $Loss$ 能通過 $p$ 傳遞給 $\Theta$ ，所以可以直接使用反向梯度傳播更新模型。

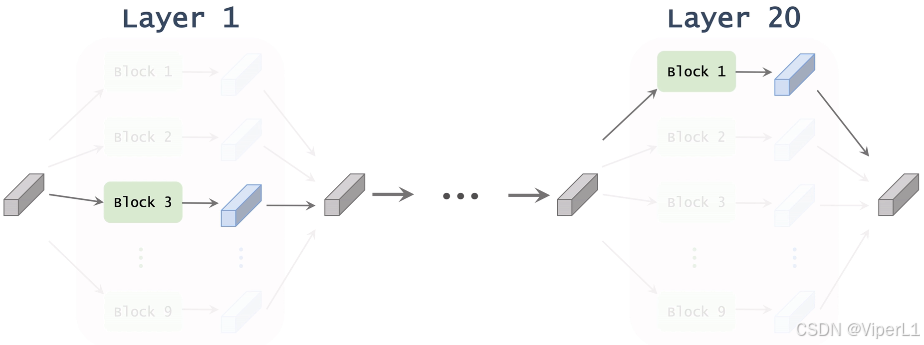
? ? ? ? 基于學習到的 $\Theta$ ，我們可以計算出superNet中沒一層中每個模塊的權重 $\alpha_j^{(l)}=\frac{exp(\theta_j^{(l)})}{\sum_{k=1}^9exp(\theta_k^{(l)})}$ ，對于每層而言，選取其中權重最大的模塊作為該層的結構，這些模塊串聯即可得到整個模型的結構，如下圖所示。

三、使用額外的性能指標優化superNet

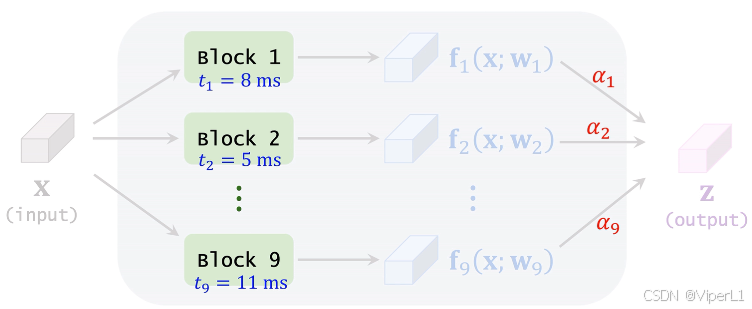
? ? ? ? 以應用于移動設備的輕量化神經網絡舉例，這類神經網絡由于需要考慮移動設備的算力限制，往往需要延遲(latency，推理時間)越小越好。

? ? ? ? 可以事先測量每個候選模塊的平均延遲，計算這一層中每個模塊的延遲加權平均 $\sum_{j=1}^9=t_j \alpha_j$ ，如下圖所示。

? ? ? ? 將20層網絡中的延遲求和，得到： $Lat(\Theta)=\sum_{l=1}^20\sum_{j=1}^9t_j^{(l)}\alpha_j^{(l)}$ ，其中 $\alpha_j^{(l)}$ 的定義在2.2節中已經給出，可以進一步記作 $Lat(\Theta)=\sum_{l=1}^20\sum_{j=1}^9t_j^{(l)}\frac{exp(\theta_j^{(l)})}{\sum_{k=1}^9exp(\theta_k^{(l)})}$ ，其中的 $t$ 為計算得到的常數。

????????損失函數為： $min_{W,\Theta}\frac{1}{n}\sum_{i=1}^nLoss(y_i,p(x_i;W,\Theta))+\lambda Lat(\Theta)$ ，其中 $\lambda$ 可以決定犧牲多少準確率來換取計算速度。

? ? ? ? 另外也可以使用 $min_{W,\Theta}\frac{1}{n}\sum_{i=1}^nLoss(y_i,p(x_i;W,\Theta))+log^{\lambda}[Lat(\Theta)]$ ，作為損失函數，效果和上式相同。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/99189.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/99189.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/99189.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！