一、反函數求導的核心公式

若函數 y = f(x) 在區間 I 上嚴格單調、可導，且其導數不等于0，則其反函數的導數為：

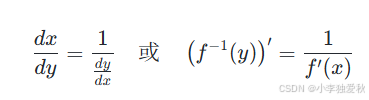
若以 x 為自變量，則公式變形為：

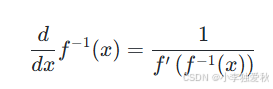
幾何意義：反函數與原函數關于 y = x 對稱，其導數互為倒數關系。

---

二、公式的嚴格條件與推導

1. 存在條件（缺一不可）：

   • ?f(x)在開區間?I上嚴格單調且連續；
   • f(x) 在 x0 處可導，且這一點導數不為0 。

2. 推導過程（基于鏈式法則）：

   

---

三、經典例題解析

---

四、高階導數與易錯點

1. 二階導數公式：

   

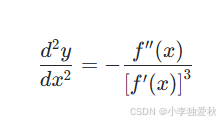
   注意：二階導數并非一階導數的簡單倒數。

2. 常見錯誤：

   • 混淆變量：如將?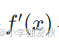?與??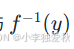的導數直接相乘)；
   • 忽略定義域：例如 y = x^2 需限定 x ≥ 0? 才可逆；
   • 誤用對稱性：圖像對稱不直接保證導數存在（需驗證可導條件）。

---

五、實際應用場景

1. 參數方程求導：

   

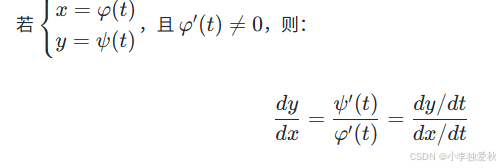
2. 工程優化：
   如船舶錨泊系統中，通過位移響應模型求反函數，快速計算錨索長度調整量。

---

六、總結

關鍵要點	說明
核心公式
單調可導條件	保證反函數存在且可導
變量一致性	嚴格區分原函數與反函數的自變量
應用擴展	參數方程、隱函數、優化控制