1.前言

? ? ? ?在 Java 中，樹（Tree）是一種非線性數據結構，由節點（Node）組成，常見的線性表則是我們之前學過的順序表、鏈表、棧、隊列等等。每個節點包含數據和指向子節點的引用。樹的常見實現方式包括二叉樹、二叉搜索樹、平衡樹（如 AVL 樹、紅黑樹）等。把它叫做樹是因為它看起來像一棵倒掛的樹，也就是說它是根朝上，而葉朝下的。

? ? ? ?數據部分和指向子節點的引用。以二叉樹為例，每個節點最多有兩個子節點（左子節點和右子節點）。樹的構建通常通過手動創建節點并連接子節點來實現。

2.節點與樹的關系

下面是一些關于樹中節點與樹之間的關系的概念，建議花三到五分鐘來看一下：

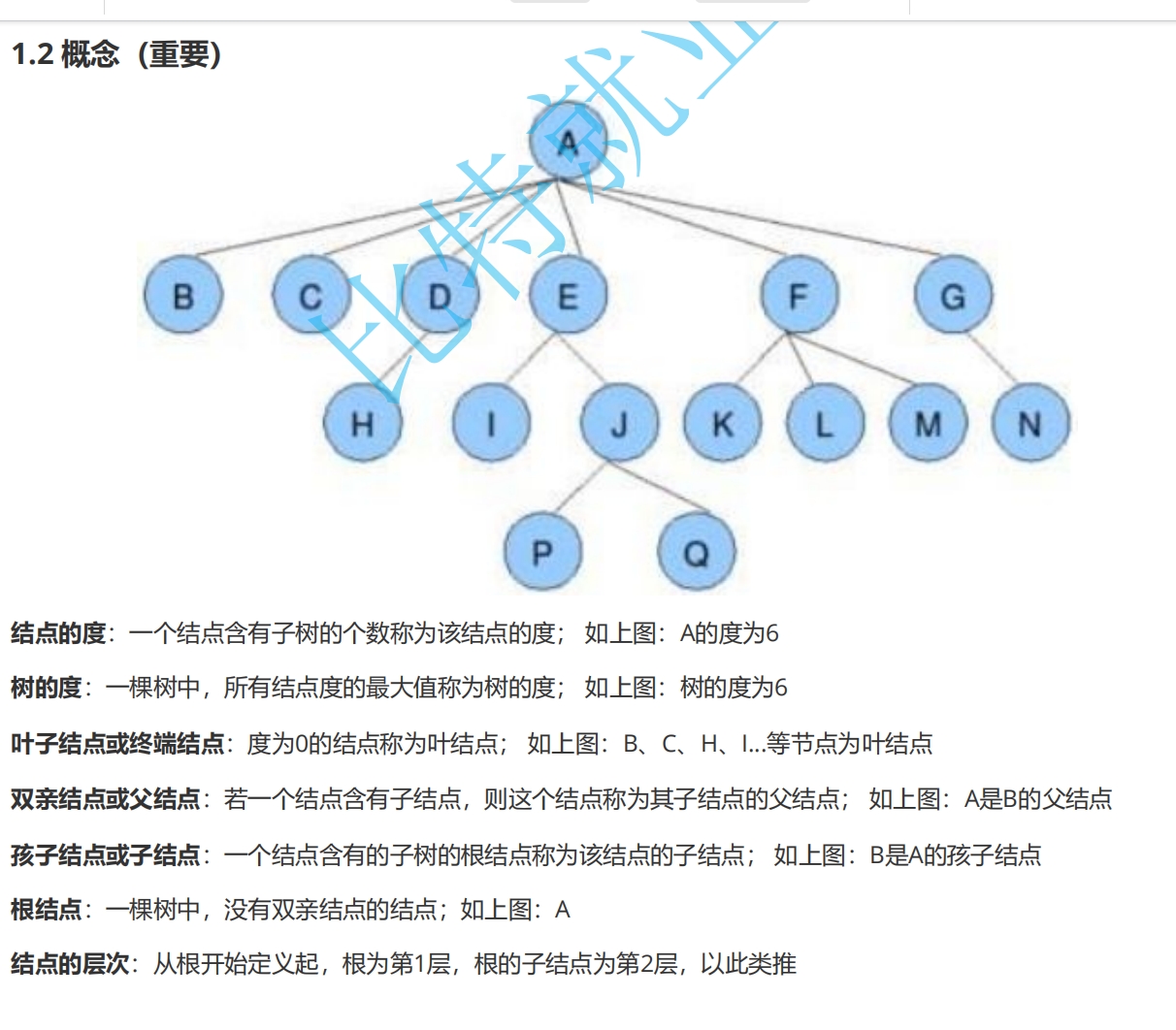
樹結構相對線性表就比較復雜了，要存儲表示起來就比較麻煩了，實際中樹有很多種表示方式，如:雙親表示法孩子表示法、孩子雙親表示法、孩子兄弟表示法等等。我們這里就簡單的了解其中最常用的孩子兄弟表示法。這部分我們只做了解，我給出部分代碼如下：

class Node f
int value;? // 樹中存儲的數據
Node firstchild;? // 第一個孩子引用
Node nextBrother;? //下一個兄弟引用

那么，樹在我們計算機中可以起到什么樣的作用呢?如下圖所示：

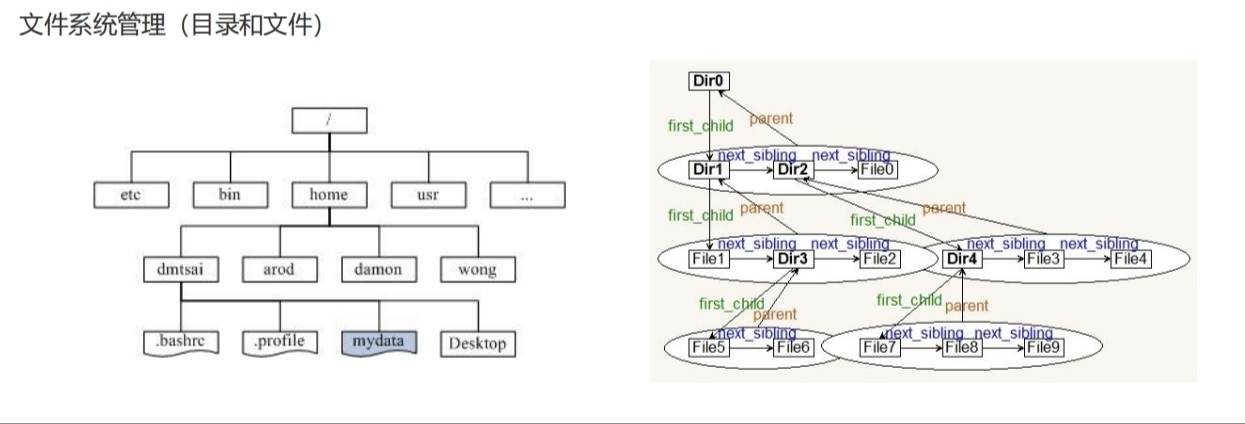
3.二叉樹（重點）

一棵二叉樹是結點的一個有限集合，該集合：

1.要么為空；

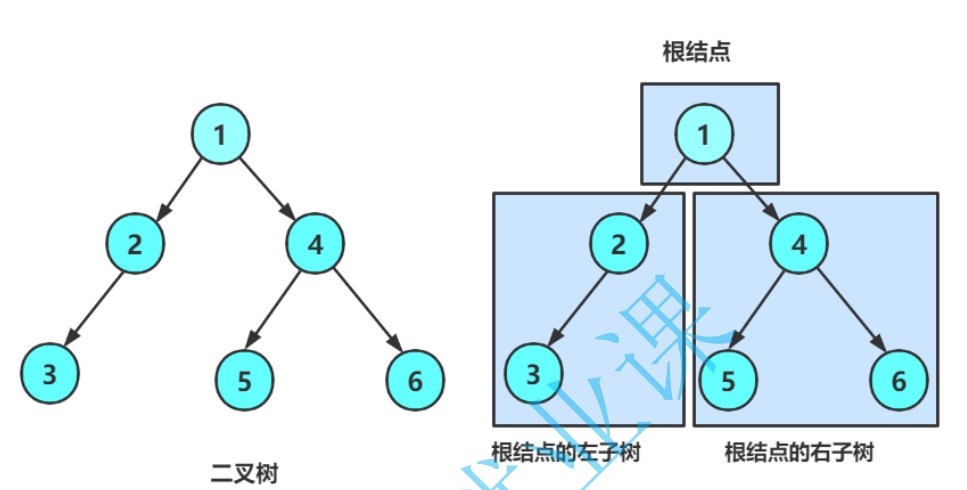
從上圖可以看出：

1. 二叉樹不存在度大于2的結點；

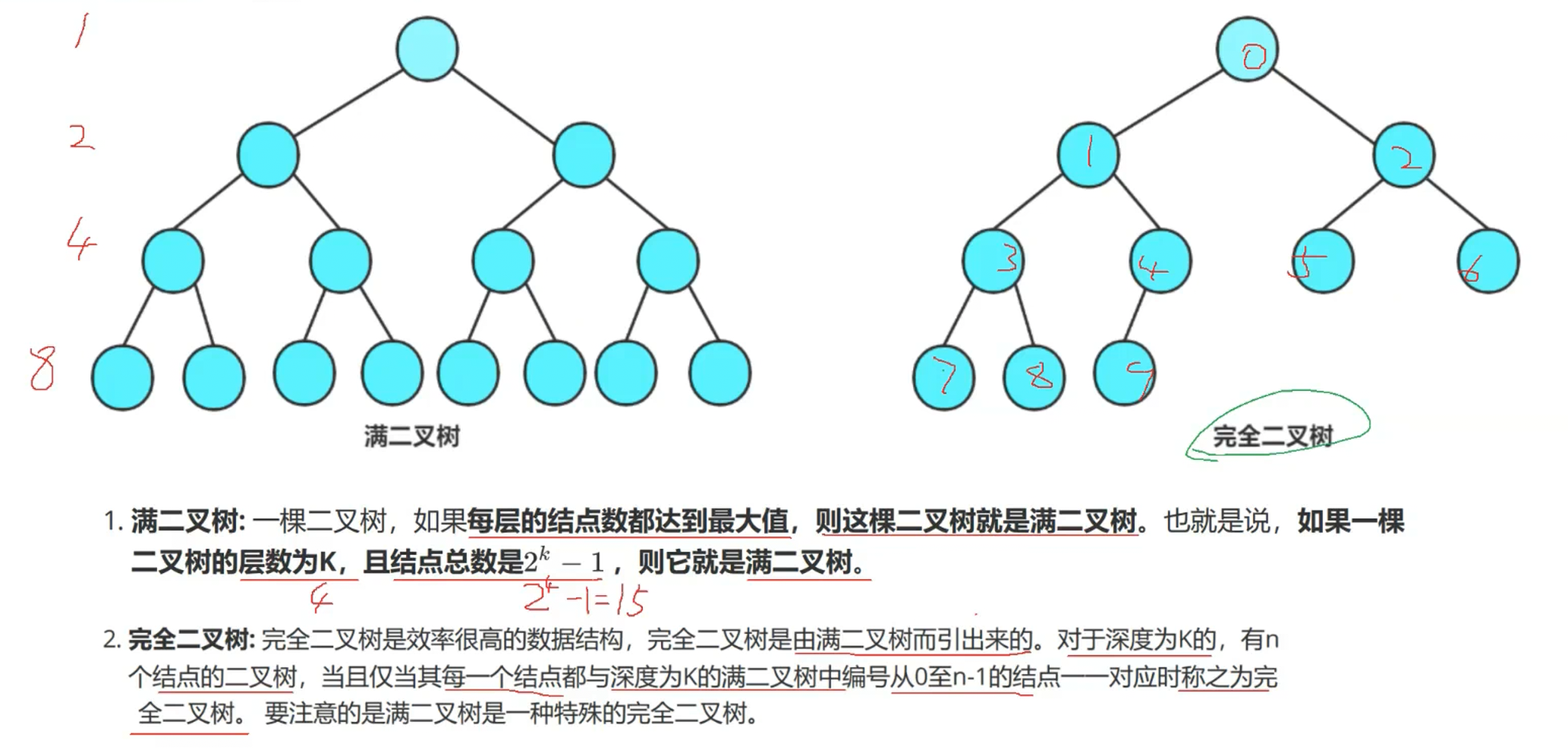
然后是二叉樹的性質，這兩大知識點理解后，能有效利于我們對于二叉樹各個點的了解與計算。

看完之后，我們來做幾道例題鞏固一下：

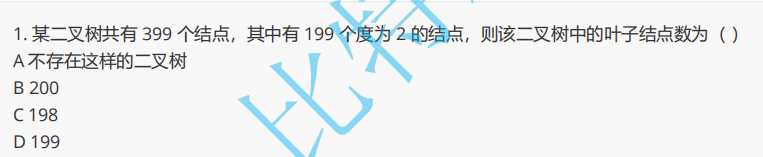
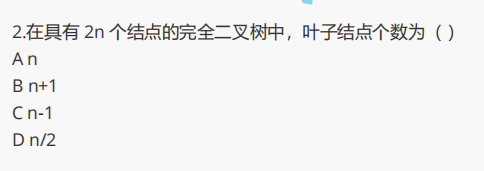
解析：第一題這里運用了 n0 = n2 + 1 的公式，就可以直接得出。第二題則需要一些公式推導，如下圖所示：

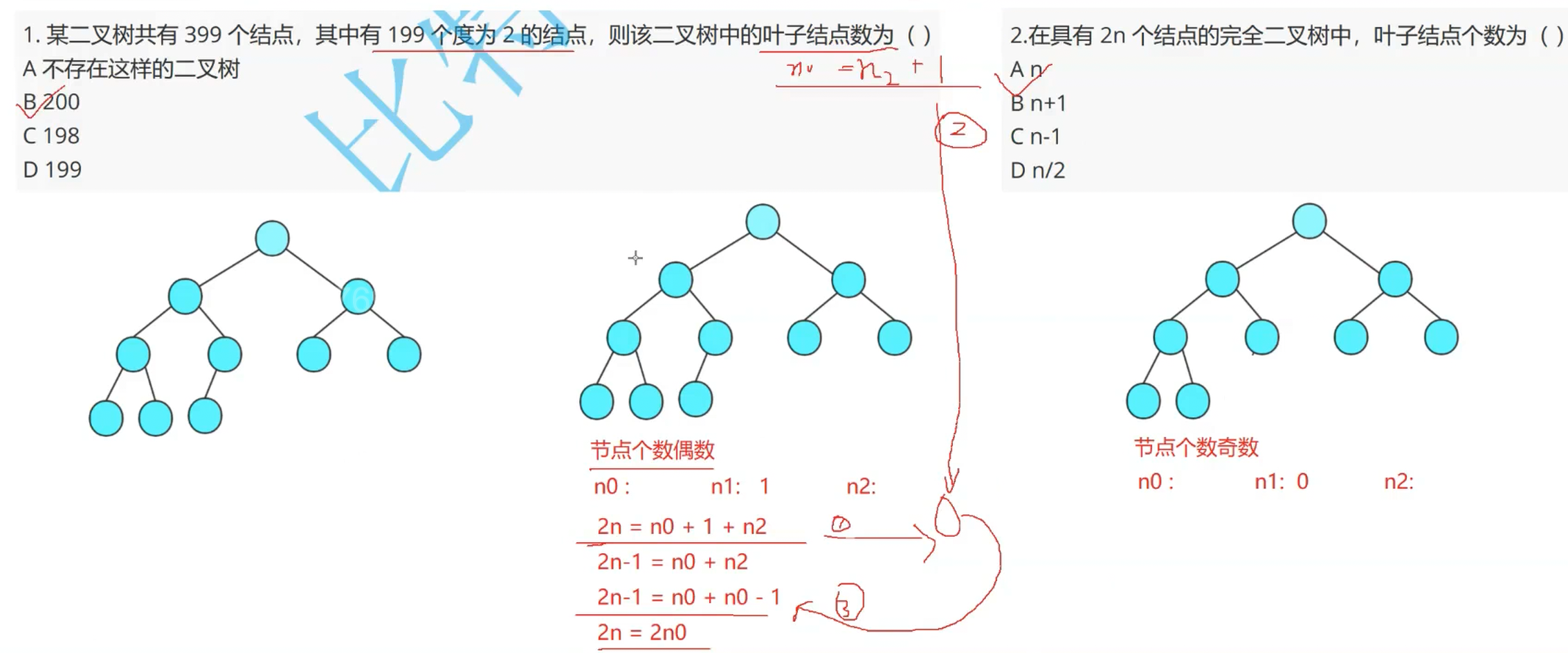
解析：具體解法與第一第二無太大區別；第四題我們就得用二叉樹性質第四點：具有n個結點的完全二叉樹的深度k為log2(n + 1)向上取整，就可得到正確答案。

3.1 二叉樹的遍歷方式

二叉樹有以下四種遍歷方式：前序遍歷、中序遍歷、后序遍歷和層序遍歷。前三個我們用的最頻繁，現在我們來一個個以圖的形式來分別看它們是如何實現的：

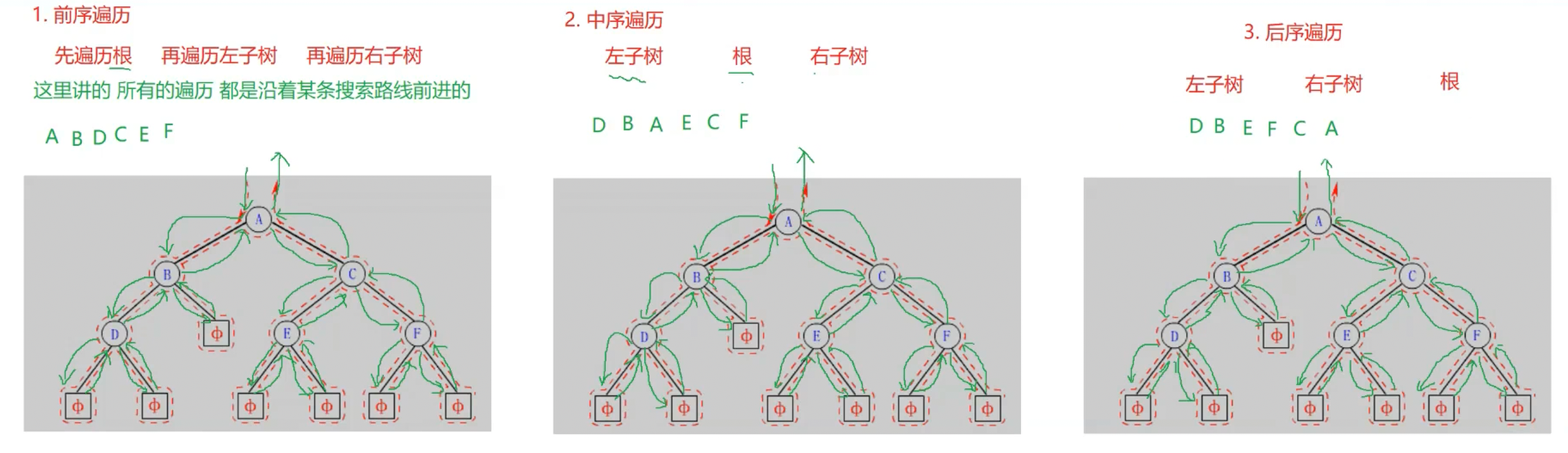
? ? ? ? 所以，前序遍歷可總結成 根 左 右 的形式來遍歷，中序遍歷則是 左 根 右 的形式，后序遍歷則是 左 右 根 的形式。層序遍歷的實現與上面三種都不相同，因此單獨來進行說明。

? ? ? ?設二叉樹的根節點所在層數為1，層序遍歷就是從所在二叉樹的根節點出發，首先訪問第一層的樹根節點，然后從左到右訪問第2層上的節點，接著是第三層的節點，以此類推，自上而下，自左至右逐層訪問樹的結點的過程就是層序遍歷。具體可看下圖：

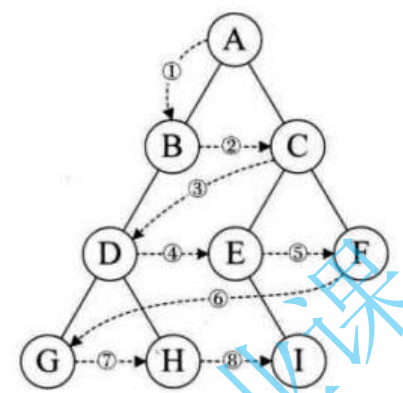
然后同樣，我們來做一些例題。

方法和經驗提示【重要】：先通過先序（前序）遍歷或后序遍歷來確定根，再從中序遍歷中找到根所在的位置，則可以得出根左邊是左樹，根右邊是右樹。

解析如下：

思考：如果有一道題給出了前序和后序遍歷，那我們是否可以得到中序遍歷呢？

答：不能！！因為前序和后序遍歷都確定的是二叉樹的根，無法確定左樹是哪些，右樹是哪些。

3.2 二叉樹的基本操作

學完了二叉樹的一些實現方式及相關概念后，就該來看看二叉樹的幾種基本操作了。

二叉樹的基本操作及要求有以下幾種：

1. 創建一棵二叉樹，并返回根節點；

2. 前序、中序、后序、層序遍歷（兩種思路：遞歸和非遞歸）；

3. 獲取樹中節點的個數（兩種思路：遍歷思路與子問題思路）；

4. 獲取樹中葉子節點的個數（兩種思路：遍歷思路與子問題思路）；

5. 獲取第K層節點的個數；

6. 獲取二叉樹的高度；

7. 檢測值為value的元素是否存在；

8. 判斷一棵樹是不是完全二叉樹；

? ? ? ?所以可以看到二叉樹的操作還是比較多的，而且都是用遞歸去實現，所以會復雜一些。我認為這其實就是二叉樹難的原因。但是大家也不要灰心，堅持下去；學完本節，數據結構可以說基本就完成了一大半了。下來我們就來分別看一看各個操作的實現：

1. 創建一棵二叉樹，并返回根節點

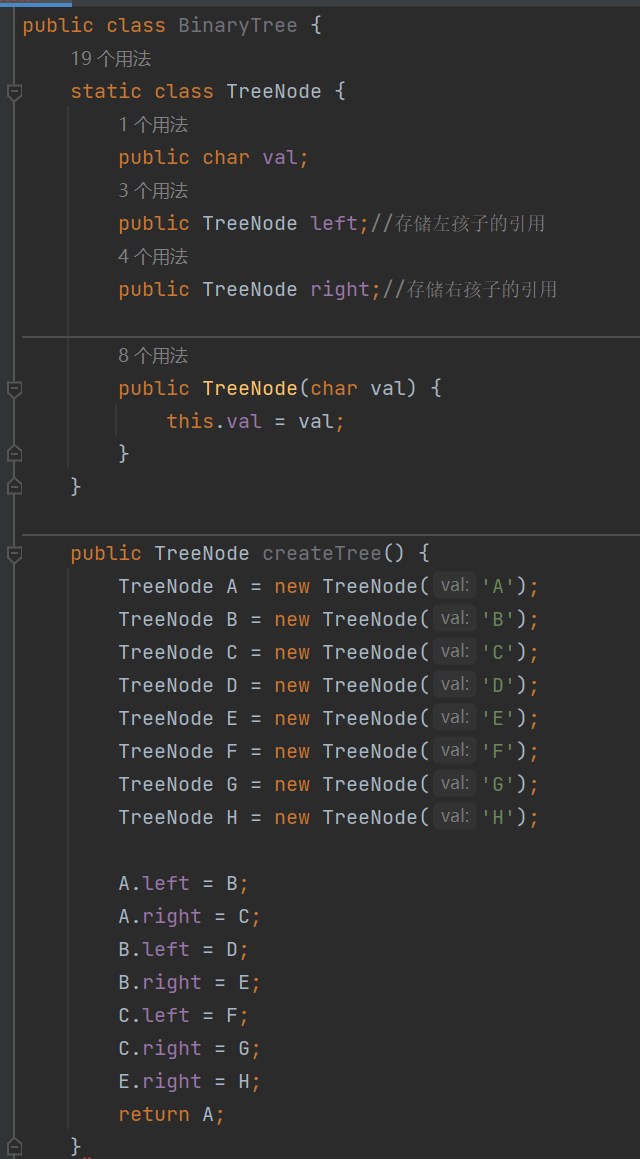
? ? ? 對于一棵二叉樹，我們肯定是有值、左樹和右樹存在的。所以我們新定義一個類叫做BinaryTree，由于在創建后就是固定的了，因此創建出靜態方法 static class TreeNode 把值、左樹和右樹創建出來，再對值用構造方法進行初始化，為什么這里不對左樹和右樹進行初始化呢？因為左樹、右樹的指向由于遞歸，它們是一直在不斷變化的，這個時候顯然用構造方法來初始化不太合理。

? ? ? ?然后接下來，我們就要創建節點了，這里就可以用實例化的方式把ABCDEFG......給創建出來，然后再定義A左樹、A右樹；B左樹、B右樹；C左樹、C右樹......具體如何創建就看個人了。

圖解代碼如下：

2. 前序、中序、后序、層序遍歷（兩種思路：遞歸和非遞歸）

2.1 前序遍歷（preOrder）【遞歸思路】

在此之前，先來復習一下遞歸的條件是：開始條件即是程序終止條件、運行時會自己調用自己。

? ? ? ?前序遍歷順序是 根 左 右 ，我們首先先來判斷一下該樹是否為空，為空則直接返回（這里由于是void，所以沒有返回值，直接寫個return即可）；然后由于是前序遍歷，我們應該首先打印出根節點的值，然后再調用自己把左樹打印出來、再把右樹打印出來，就可以完成遍歷。它會將所有的根先打印完后（說明它會一直向下、然后打印根? ?向下、然后打印根，直到沒有根可以被打印時），就會去打印左樹、再去打印右樹。

2.2 前序遍歷（preOrder）【非遞歸思路】

? ? ? ?非遞歸思路這里使用的是棧來完成的，條件仍然是判斷一下該樹是否為空，為空則直接返回。然后我們需要創建一個棧，才能完成操作，具體可以寫成 Stack<TreeNode> stack = new Stack<>();

? ? ? ?由于這里是采用非遞歸的方式進行遍歷，因為遞歸的整體流程與循環比較類似，所以我們可以使用循環來取代遞歸。那么就要先想到循環的條件應該是什么，這里我們可以定義一個指針cur等于根節點?（根節點是root） ，讓cur來執行 根 左 右 的順序并打印，那么循環條件其實就應該是cur != null ，因為如果為空就證明沒有 根節點/左樹/右樹 了。

? ? ? ?具體就是：每往下走一個，就把cur放到棧里面，并進行打印，然后讓 cur = cur.left ,直到為空的時候是不是就不進入循環了，這里我們就要想如何從左樹轉到右樹。這里我們就用到棧中的方法stack.pop() 進行彈出（這里可以定義一個top，用于接收pop()的值），然后再令 cur = top.right 就能過渡到右樹來了，但是此時有一個問題，過渡到右樹來我們是不是也是為了去遍歷？那我們剛才這樣寫只執行了一次（沒有寫成循環的形式），那該怎么辦呢？

答：再來一個循環，形成嵌套循環。

? ? ? ?我們可以寫成嵌套循環的形式，在原來的 while (cur != null) {? ?之上再來一個循環，那么同樣的，我們要思考循環條件是什么。大家想想。既然每次是需要放棧才打印，出棧到右樹，右樹為空時又會出棧。那么是不是總有一次棧就會一直出出出，最后變為空了呢。所以我們的條件應該是會反其道而行之，即?!stack.isEmpty()，然后由于 根 左 順序時循環條件是 cur != null，則到右樹時也不應該去掉。然后如果兩個條件中我們應該使用的是或者（||），只要滿足一個就終止程序。即完整的循環條件是?while (cur != null || !stack.isEmpty() 。

具體代碼實現如下：

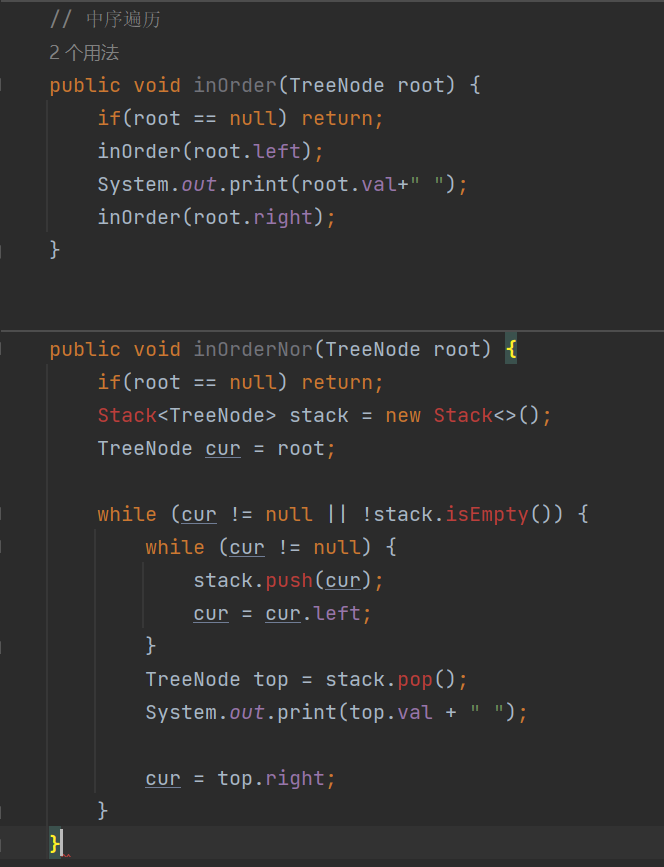
2.3 中序遍歷（inOrder）【遞歸思路和非遞歸思路】

中序和后序遍歷它們與前序思路基本相同，所以這里就不再贅述，大家可以自己嘗試一下，看能不能寫出來，數據結構重要的就是多畫圖、多寫、多想。

我把遞歸思路和非遞歸思路的代碼放在一起了，實現如下：

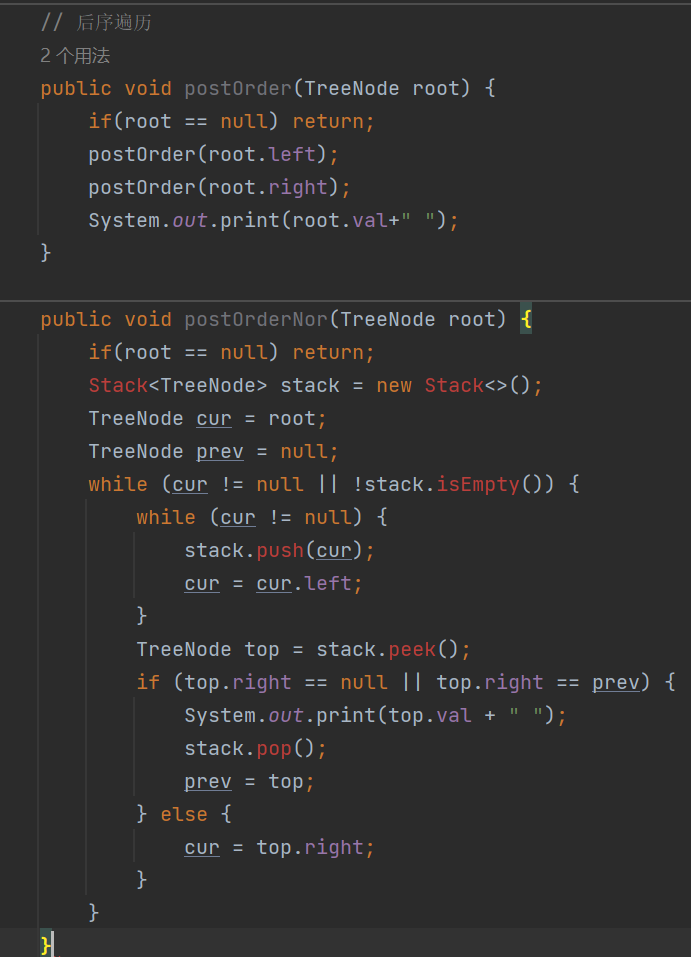
2.4?后序遍歷（postOrder）【遞歸思路和非遞歸思路】

同樣放在一起，如下：

2.5 層序遍歷

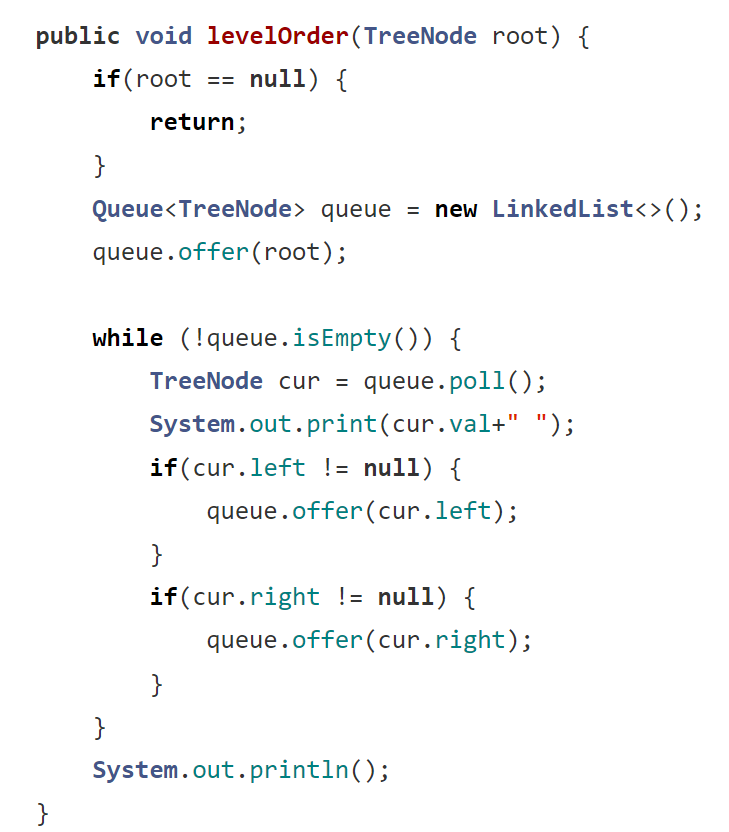
? ? ? ?層序遍歷我們是使用隊列的方式進行實現，隊列的特點是“先入先出”，如果用棧的話，由于特點是“先入后出”，所以就不可能先打印出A（假如一棵樹是ABCDEFG）。所以必須要使用隊列才能完成。

? ? ? ?在此之前，我們也是要判斷一下樹本身是否為空的情況。判斷好了之后，因為我們使用隊列來實現，所以我們要先創建隊列。隊列創建好了之后，我們應該先把根節點手動放到隊列里面。由于這種也是屬于非遞歸實現的，所以要使用循環；我們的思路是這樣的：因為已經放了根節點，所以先把根節點彈出并打印值，然后再判斷 左/右 樹是否是非空，是非空我們就放到隊列中一直循環。所以這里的循環條件應該是隊列不為空。

那么思路已經告訴你了，接下來就自己試一試，參考代碼如下：

3. 獲取樹中節點的個數（兩種思路：遍歷思路與子問題思路）

3.1?獲取樹中節點的個數（遍歷思路）

遍歷的思路比較簡單（這里默認以前序遍歷為例，下同），我們可以設置一個指針，每遍歷了一個節點就 ++ 一下，直到以 根 左 右 的順序遍歷完成，就停止程序，條件與前序遍歷條件一致。需要注意的是，指針不能在遞歸方法中創建，不然的話每次遞歸就都會創建一個新的指針，就無法達到預期要求。因此我們應該創建在外部，并用 static int 修飾。大家可以自己嘗試一下，并不是很難。

具體代碼如下：

3.2?獲取樹中節點的個數（子問題思路）

? ? ? ?子問題思路就是把一個大問題轉化成幾個小問題，然后再根據代碼思想進行實現，這樣有時候問題執行效率會快一些。

? ? ? ?本題的子問題思路就是以 根 左 右 的方式把一棵二叉樹分成三份，條件是root = null（該樹為空樹的情況） ，由于根節點只有一個，所以獲取樹中節點數可以理解成? 左樹數量 + 右樹數量 + 1 。而左樹和右樹計算有多少個這里我們還是使用遞歸的方式，但是這里我們是直接?return size2(root.left) + size2(root.right)+1 來得到，如圖所示：

所以可以看到，這里我們是以遞歸執行次數來判斷節點數的，每次遞歸一次，節點數就多一個，以此類推。所以比較巧妙。

4. 獲取樹中葉子節點的個數（遍歷思路與子問題思路）

4.1?獲取樹中葉子節點的個數（遍歷思路）

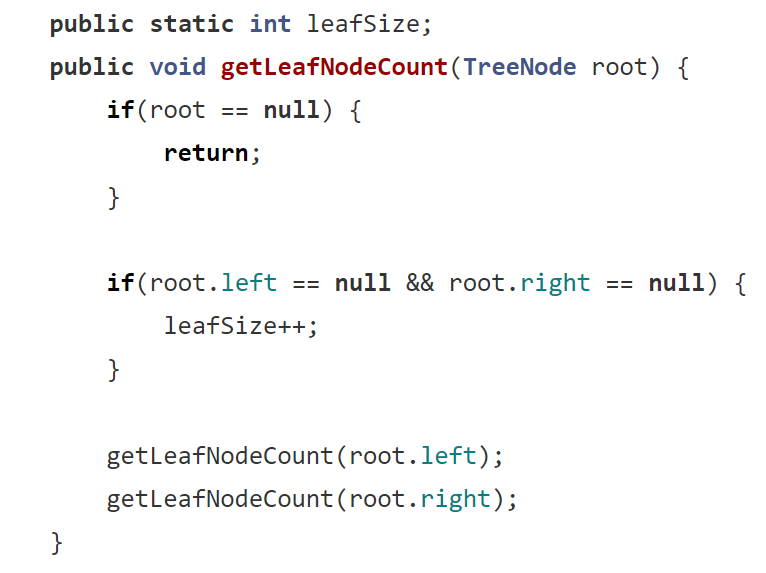
? ? ? 與獲取樹中節點的個數思路有點類似，同樣也是要設置一個指針（用 static int 修飾），遇到葉子節點就 ++ 一下。那么指針什么時候遇到的節點才是葉子節點呢？我們就得想想葉子結點的含義。（這里忘記了可以往前面翻一下，有目錄，我這里由于篇幅，就不再闡述）

? ? ? 所以由葉子結點定義可知，左右樹都沒有節點的節點就是葉子節點，因此我們遞歸時它 ++ 的條件就應該是if(root.left == null && root.right == null) ，然后在這之前還是一樣if(root == null) 判斷樹為空樹的情況，最后再把遞歸方法寫上就可以了。如圖：

4.2?獲取樹中葉子節點的個數（子問題思路）

同樣與獲取樹中節點的個數思路相差不大，需要注意的是由于沒有指針的幫助，那我們就應該把方法寫成有返回值的，最后再直接返回葉子結點個數就行了。

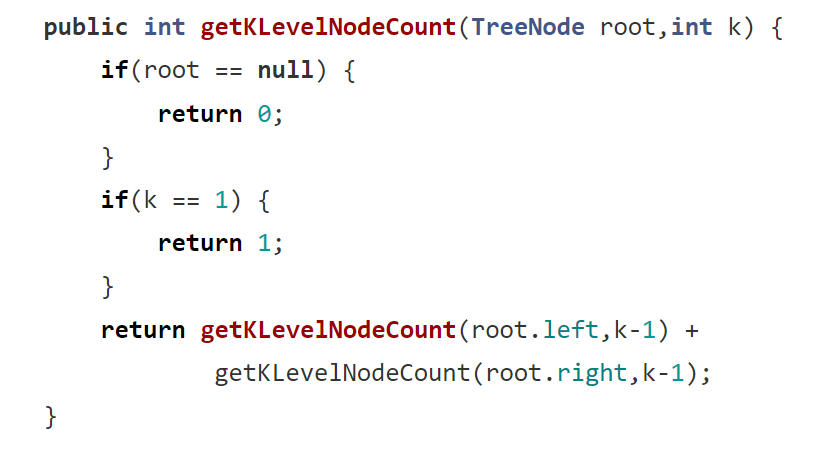
5. 獲取第K層節點的個數

? ? ? ?這里也是可以用子問題來解答，但沒有使用指針，所以我們就用返回值來弄。順帶一提，不要考慮你怎么調用到第K層，這個是方法里已經實現了的。你只需要專注于如何獲取第K層節點的個數就可以了。

6. 獲取二叉樹的高度

這里我們的思路是，把左樹高度和右樹高度各自都用一個變量來接受，最后比較就可以得到預期結果。

7. 檢測值為value的元素是否存在

? ? ? ?既然是要找值是否存在，那么根節點就是該值的情況和樹為空的情況我們需要注意去判斷一下，該方法findVal(TreeNode root,char val) 它的方法內部就可以直接查找值，我們要做的就是預防或處理各種情況的發生。順帶一提，使用該方法的時候就構成了遞歸。

? ? ? ?我們可以將找到了該值的節點用變量來接收，因為已經判斷了根節點就是該值的情況，那么在遞歸的時候，不斷往下走就會變成判斷下面的節點是否是我們需要尋找的值；所以我們只需要判斷有找到和沒有找到的情況即可。

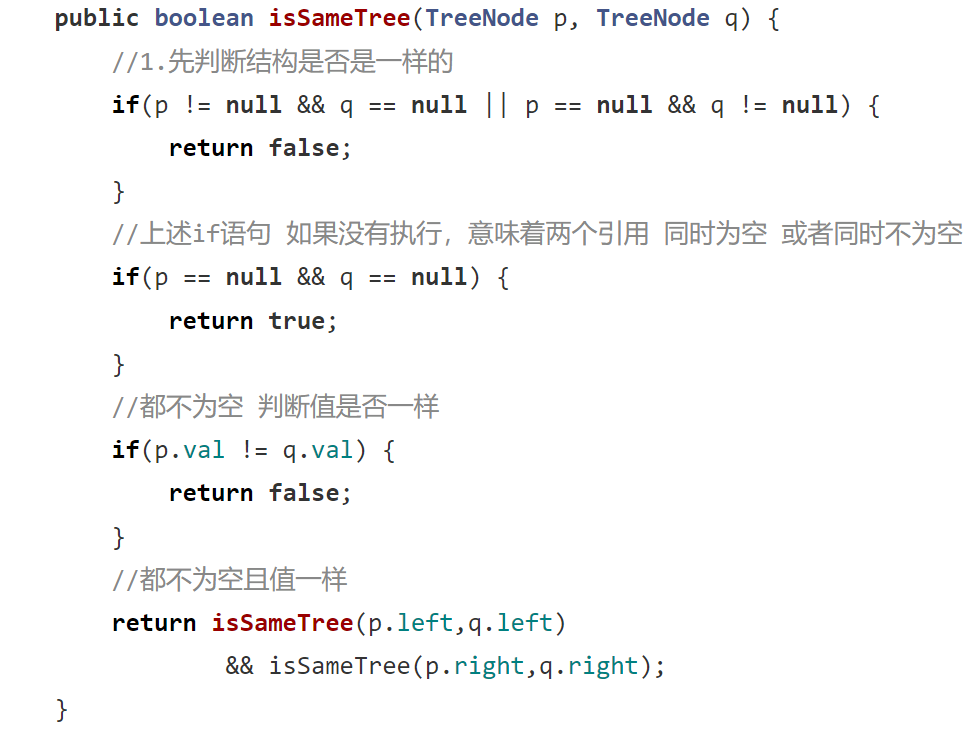
8. 判斷一棵樹是不是完全二叉樹

這里僅給出參考代碼，不做思路說明，大家可以自己嘗試一下。

至此。二叉樹的所有基本操作我們都完成了，下面就要開始練題了。練題的時候某些題目不要死磕，實在不會就看一下參考答案。還有就是要多畫圖，這樣能更方便的去理解。

3.3 二叉樹的相關題型

這里給出的題目都是力扣或牛客網里的，在大家學完數據結構的時候就可以在這里刷題了。

由于篇幅原因，思路和代碼都以圖的形式來呈現。

1.??572. 另一棵樹的子樹 - 力扣（LeetCode）

提示：這里用到了? 8. 判斷一棵樹是不是完全二叉樹? 的相關代碼。

思路（先自己去想，不會再來看一下思路，看完思路還不會就看答案吧）：

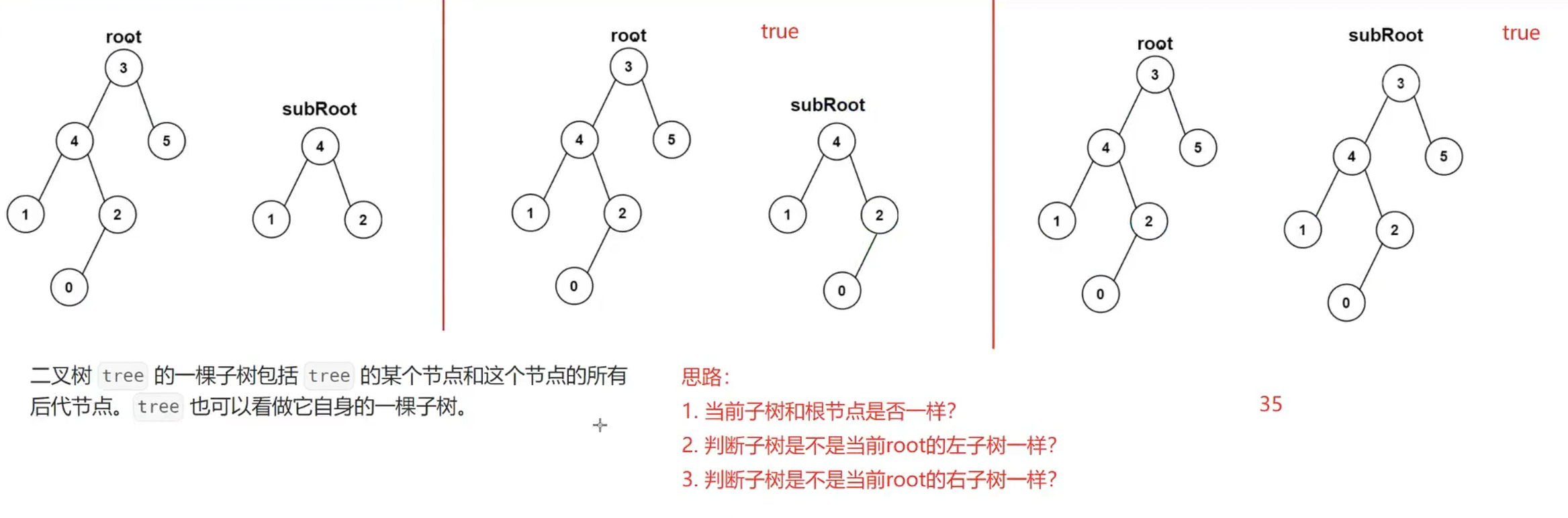
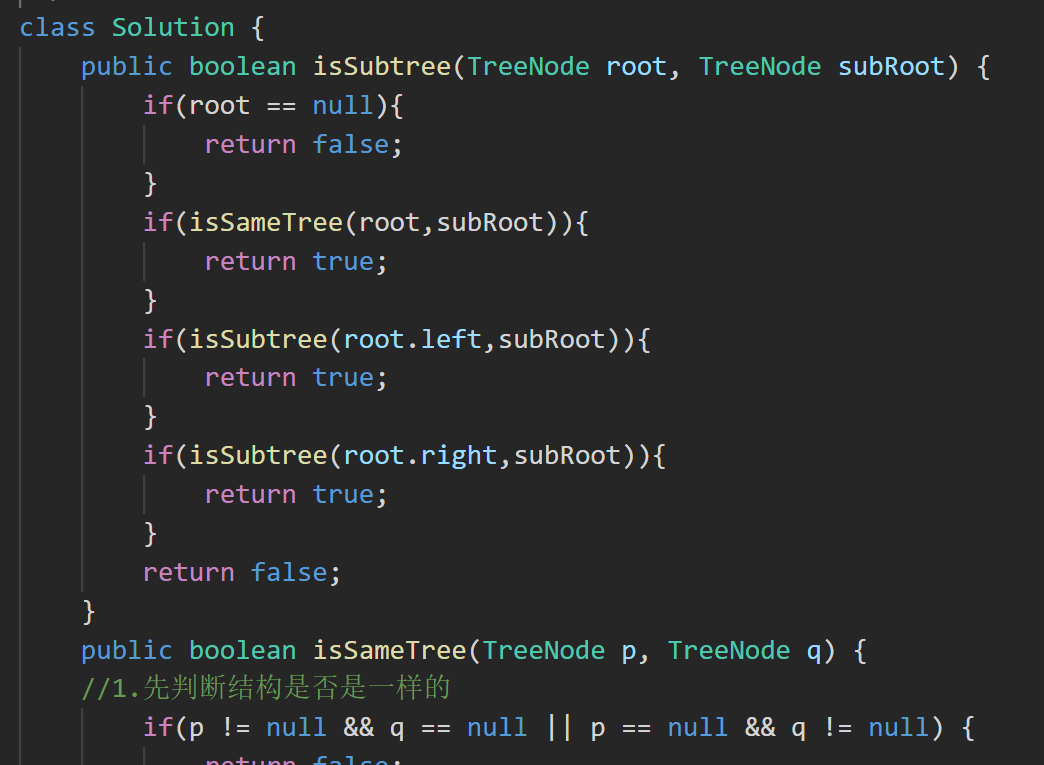
答案：在 boolean isSameTree(TreeNode p, TreeNode q) 之下的都是??8. 判斷一棵樹是不是完全二叉樹? ?的代碼。

2.??101. 對稱二叉樹 - 力扣（LeetCode）

思路：

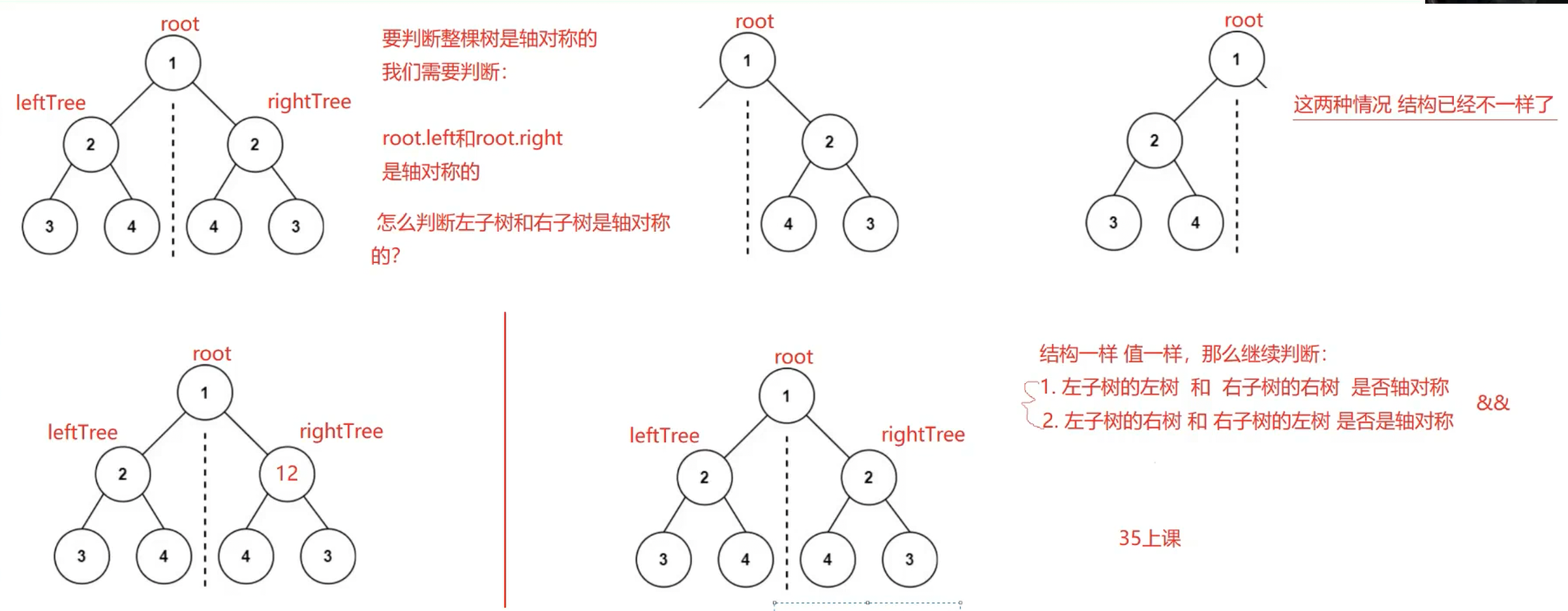
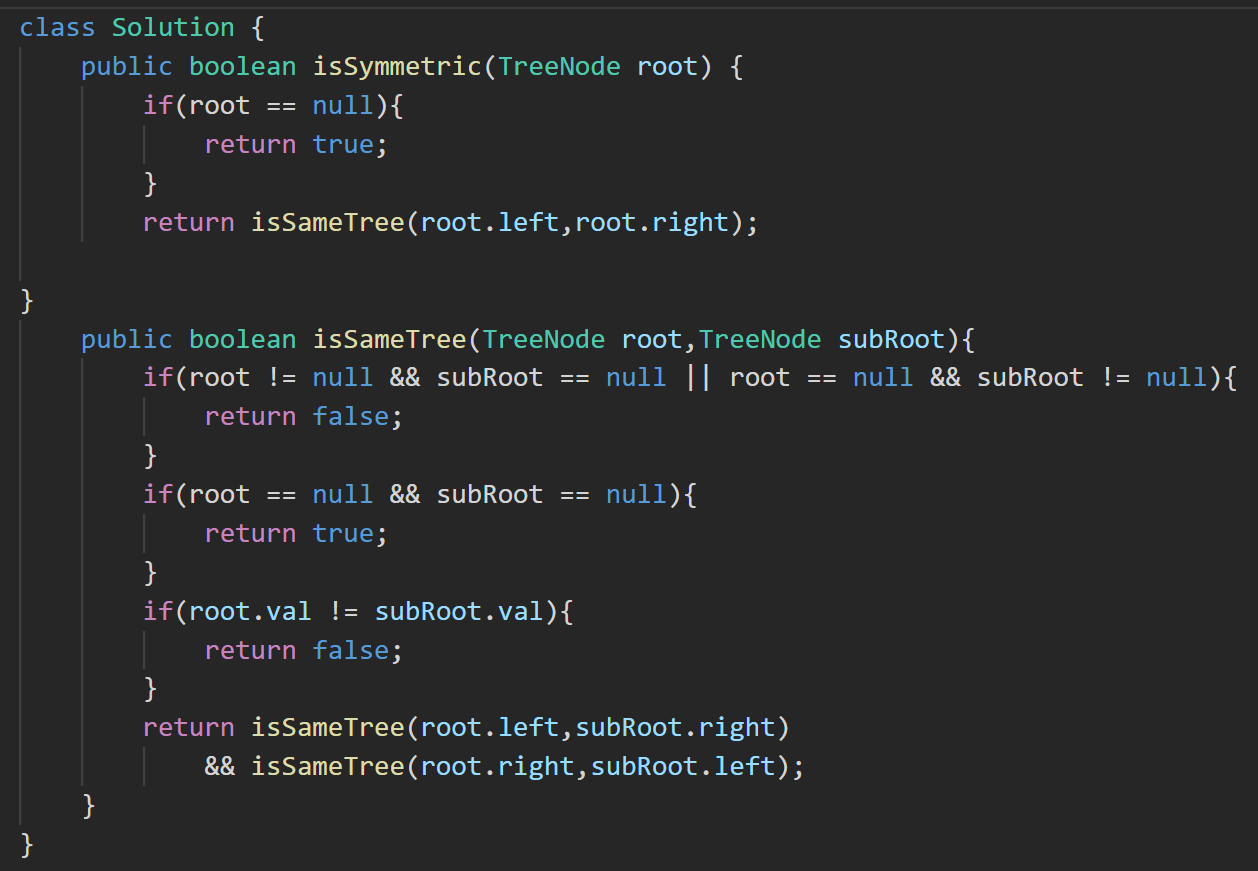
答案：

3.??100. 相同的樹 - 力扣（LeetCode）

思路：

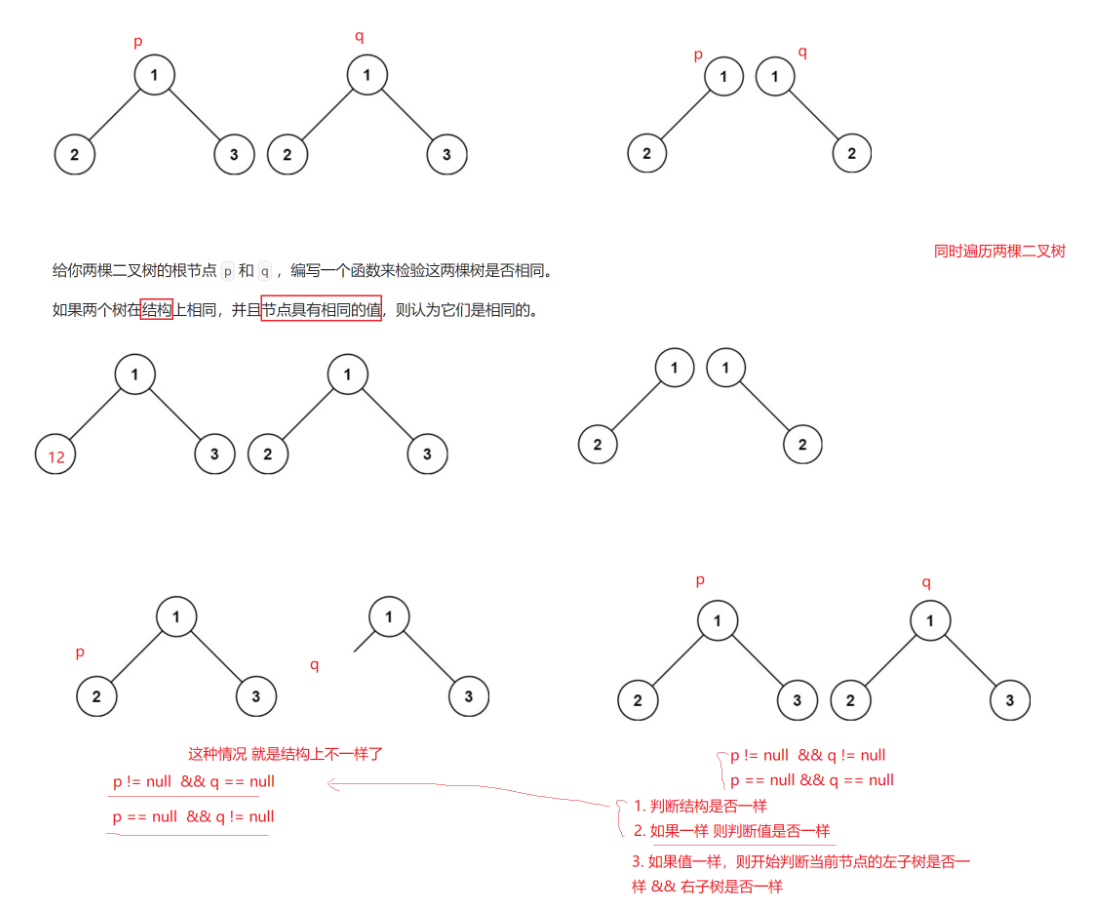
答案：

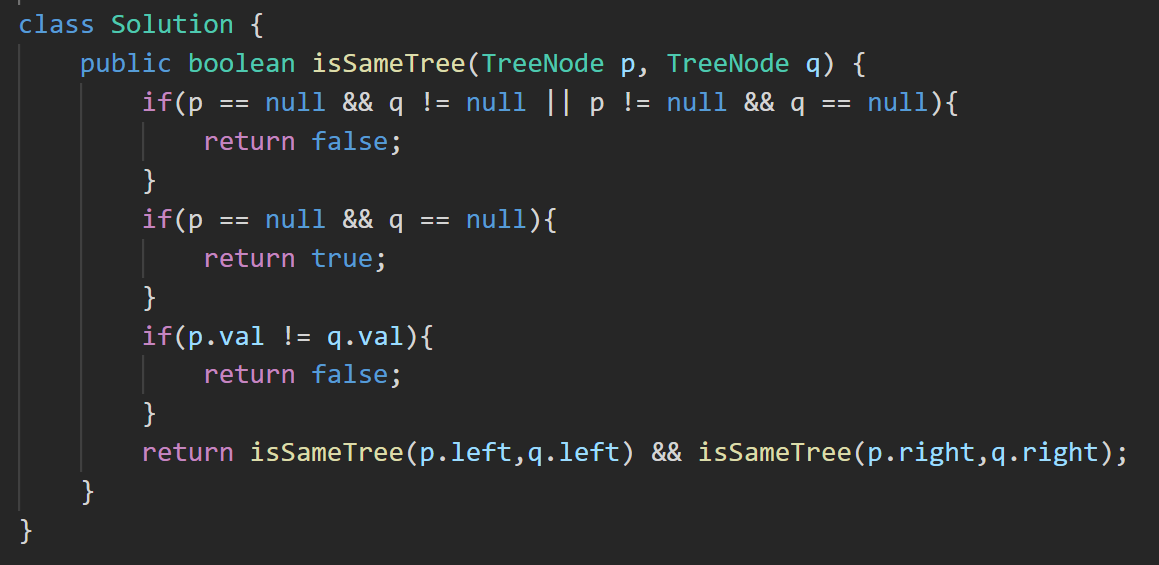
ps：雖然思路看上去很長，但寫成代碼卻沒有幾行就搞定了。

4.??226. 翻轉二叉樹 - 力扣（LeetCode）

思路：

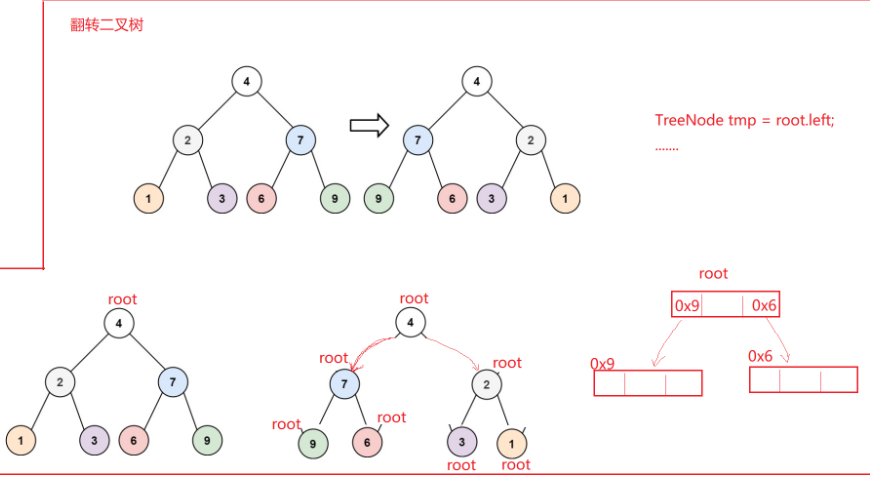
答案：

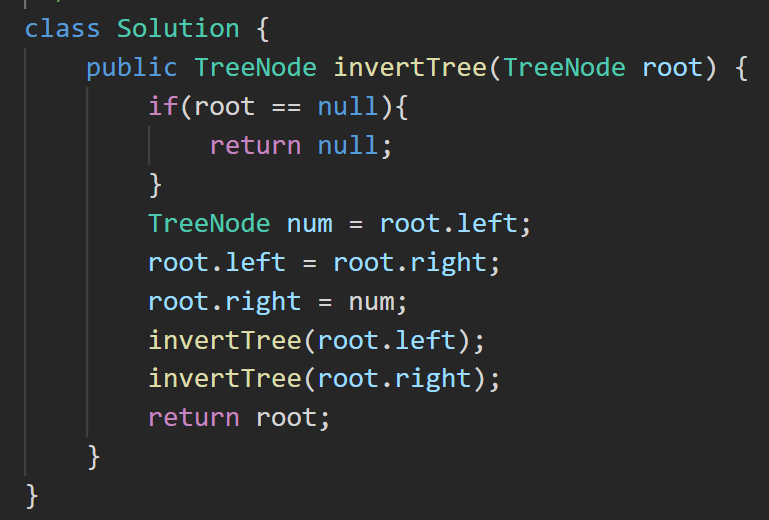
5.??110. 平衡二叉樹 - 力扣（LeetCode）

思路：

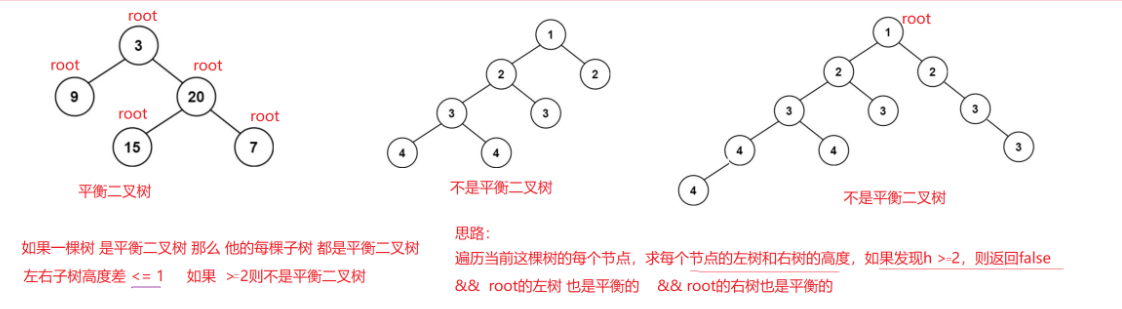
答案:

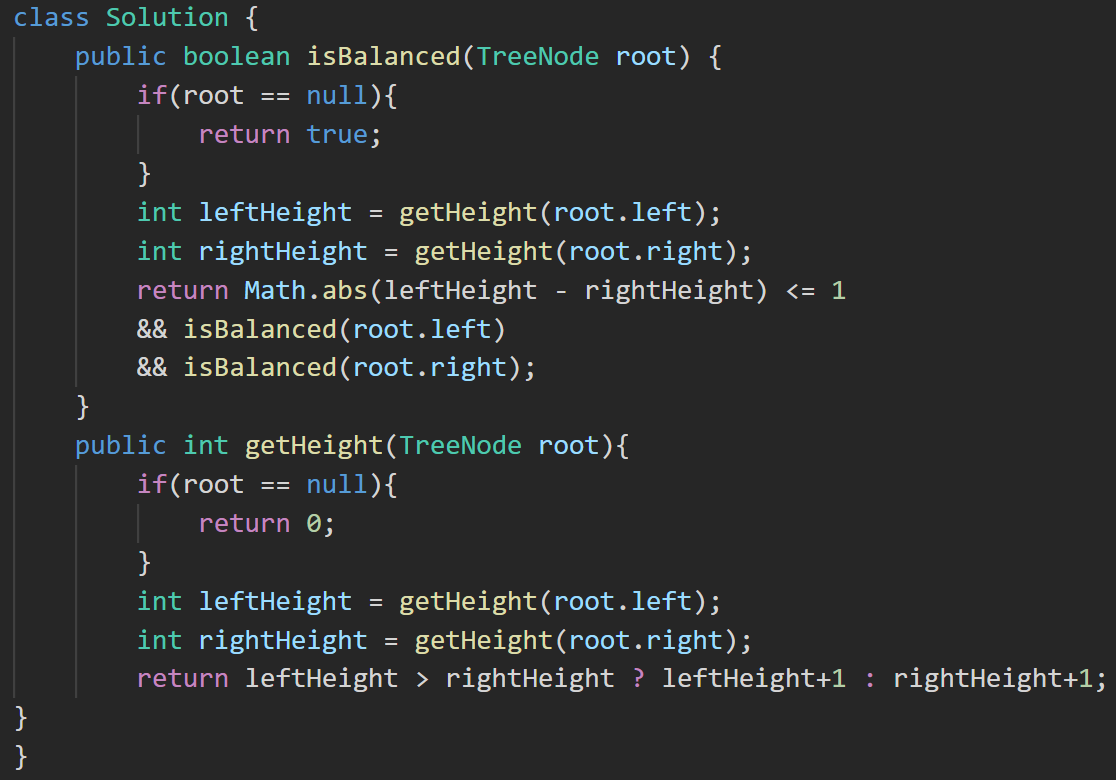
6.?94. 二叉樹的中序遍歷 - 力扣（LeetCode）

提示：本題是使用非遞歸方法實現的。

答案：

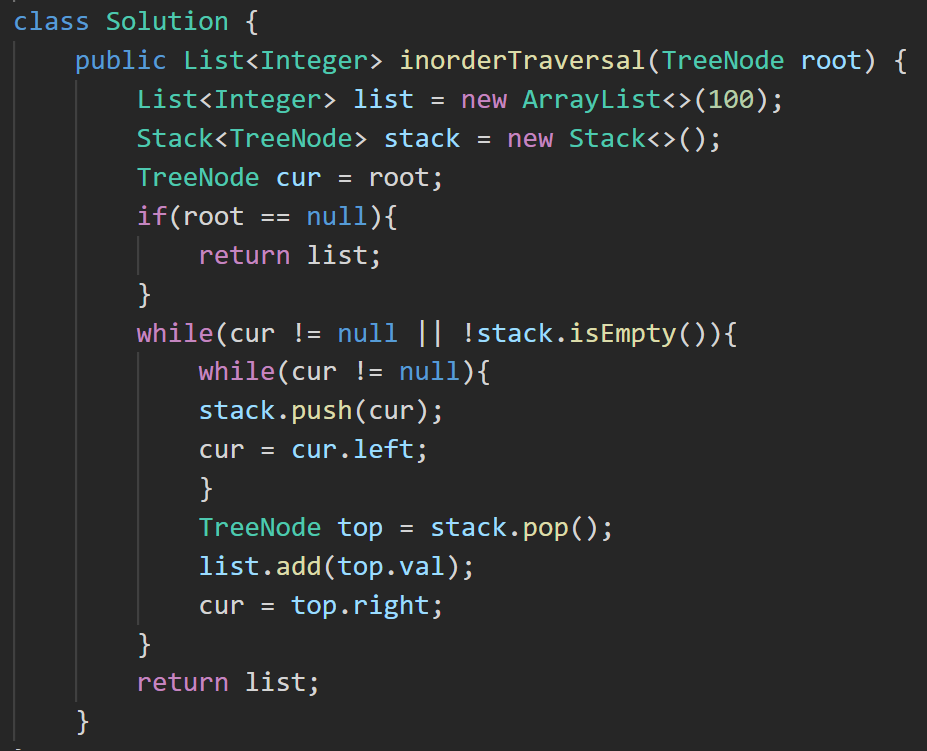
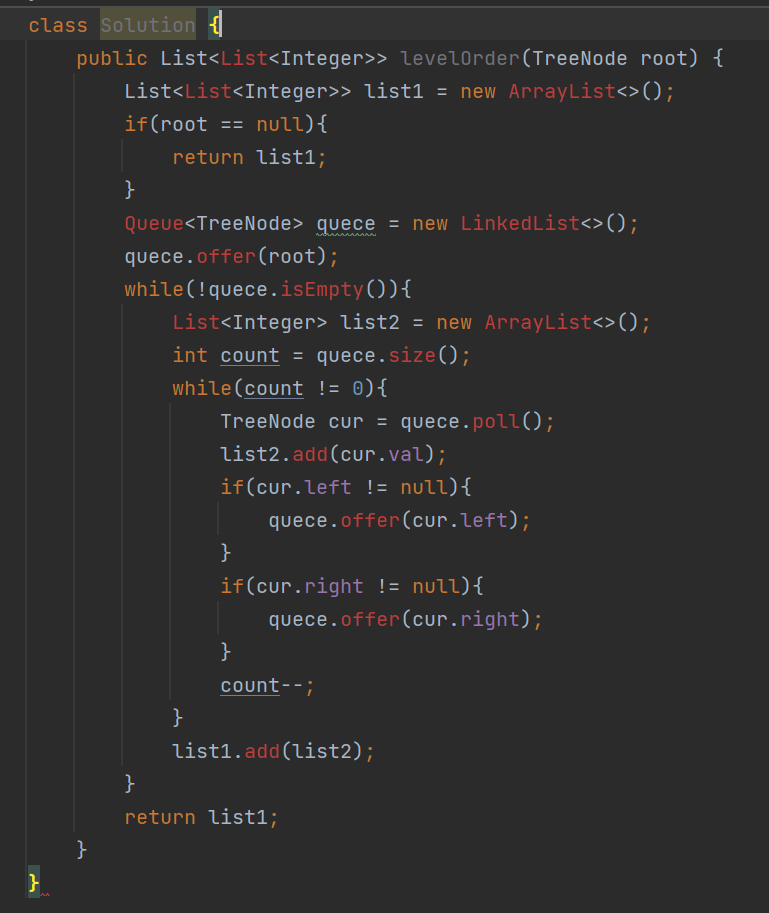
6.??102. 二叉樹的層序遍歷 - 力扣（LeetCode）【本題開始會需要一些腦回路】

思路：

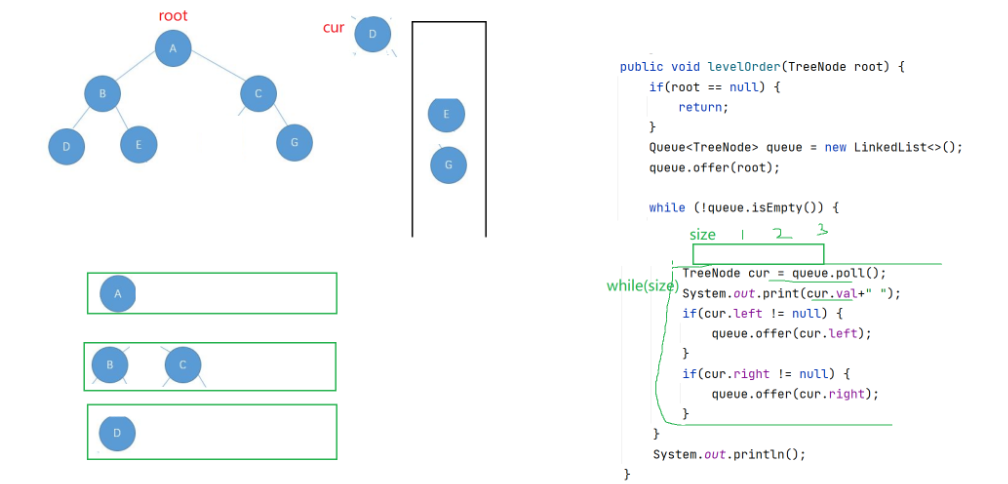
答案：

那么，本篇文章到此結束！

本篇文章的截圖部分摘自于比特科技 。希望能對你有幫助。