簡介

判斷點與多邊形位置關系算法是幾何算法中最基礎的算法之一，包括布爾運算在內的非常非常多的算法都會用到它。它的穩定是算法庫穩定的關鍵。

下面我們從一個邊都是直線的多邊形開始了解射線法的原理。然后看看引入曲線后會帶來哪些問題，以及在實際應用還有哪些其他問題。最后看看如何實現一個穩定的，支持曲線邊多邊形的點與多邊形位置關系算法。

射線法

講射線法的資料很多，用AI也能輕松查到詳細內容，所以我們只簡單介紹一下重點，為后面內容做個鋪墊。

射線法的實現思路是以被檢測點為起點做一條射線，看和多邊形有幾個交點，奇數個交點說明在內部，偶數個交點說明在外部（0算偶數）。

實際中往往以x軸正方向做射線，這樣計算比較簡單。

交點計數時，要考慮各種相交類型，例如射線和邊重合，射線過頂點等。

有一個已經總結好的的原則可以直接使用（以x軸正方向射線為例）：

當邊的一個頂點的y大于參考點的y，另一個頂點的y不大于參考點的y（等于或小于），且邊與x軸交點的x大于參考點的x時計數加一。

如何判斷點是否在多邊形上呢？因為一般這個判斷都需要帶一個精度，所以直接用上面介紹方法中的得到的邊與x軸交點到參考點x的距離是不準確的。

我見過兩種方式：

一種是單獨判斷點是否在邊上。

另一種是點加上精度會得到一個Box，用這個Box的頂點分別做射線法，如果有些頂點為內部，有些頂點為外部則認為是點在多邊形上邊。

兩種方法適用的是不同的場景，大家按需選擇。

曲線邊給基礎射線法穩定性帶來的挑戰

首先曲線與射線相交可能會有多個交點，我們就不能只拿曲線的兩個端點來判斷了，而是要根據交點位置曲線是否穿過射線來判斷是否計數加一。

是否穿過一般用交點處的切線方向來判斷。但如果曲線和切線相切時，就需要根據二階導數甚至更高階導數來判斷穿過關系了。

但相切本身就是個帶精度判斷的問題。一階導數小于多少用二階導數，二階導數小于多少用三階導數。這個沒有唯一的結論。一個場景對了，另一個場景可能就不對了。

另外，相切時，因為精度的問題，我們幾乎不可能計算到恰巧相切的點。不是偏左點就是偏右點，甚至參數域上偏很多都有可能。如果曲線曲率很大，這個偏差也可能對切線方向帶來比較大的影響，從而影響穩定性。

還有就是，邊都是直線時，我們可以保證各邊之間無縫連接。是曲線時就很難保證無縫連接了。原因是因為曲線的表示方式導致的。

例如畫圖時我們用三點定義圓弧，但圓弧在內存中存儲時用圓心半徑和角度。那么我們根據三點計算出的圓心半徑和角度再反算回三點時，在特殊場景中是存在誤差的。這個誤差就會導致邊連接處存在一個小小的縫隙，這個小小的縫隙出現在射線附近時就有可能導致錯誤。

有些算法庫，多邊形是其他運算的結果（例如布爾運算），本身可能就帶符合誤差要求的縫隙（因為有可能基于效率原因考慮不做縫隙修復）。

上面提到的情況絕對不是危言聳聽，都是我們在實際項目中碰到過的。算法本身不難，難的是如何在各種場景下都能表現的穩定。

為了給大家對上面說的有個更直觀的認識，我畫了個草圖放到下面。

穩定的射線法

基于前面的討論，相切或接近相切時，從理論上就是不能解決的。

一個最簡單的解決思路是，檢測上述情況，發現出現了就再換一條射線。

從概率上，這種算法沒問題。但多邊形復雜時，有可能需要換好幾次射線才能得出結果。另外，如果射線不是x軸或y軸方向時，直線和曲線求交的效率也會下降。

下面介紹一下我們設計的算法思路。

1. y軸正方向做射線，計算所有交點。

2. 根據交點統計計數和可信度，可信度符合要求則直接返回結果。

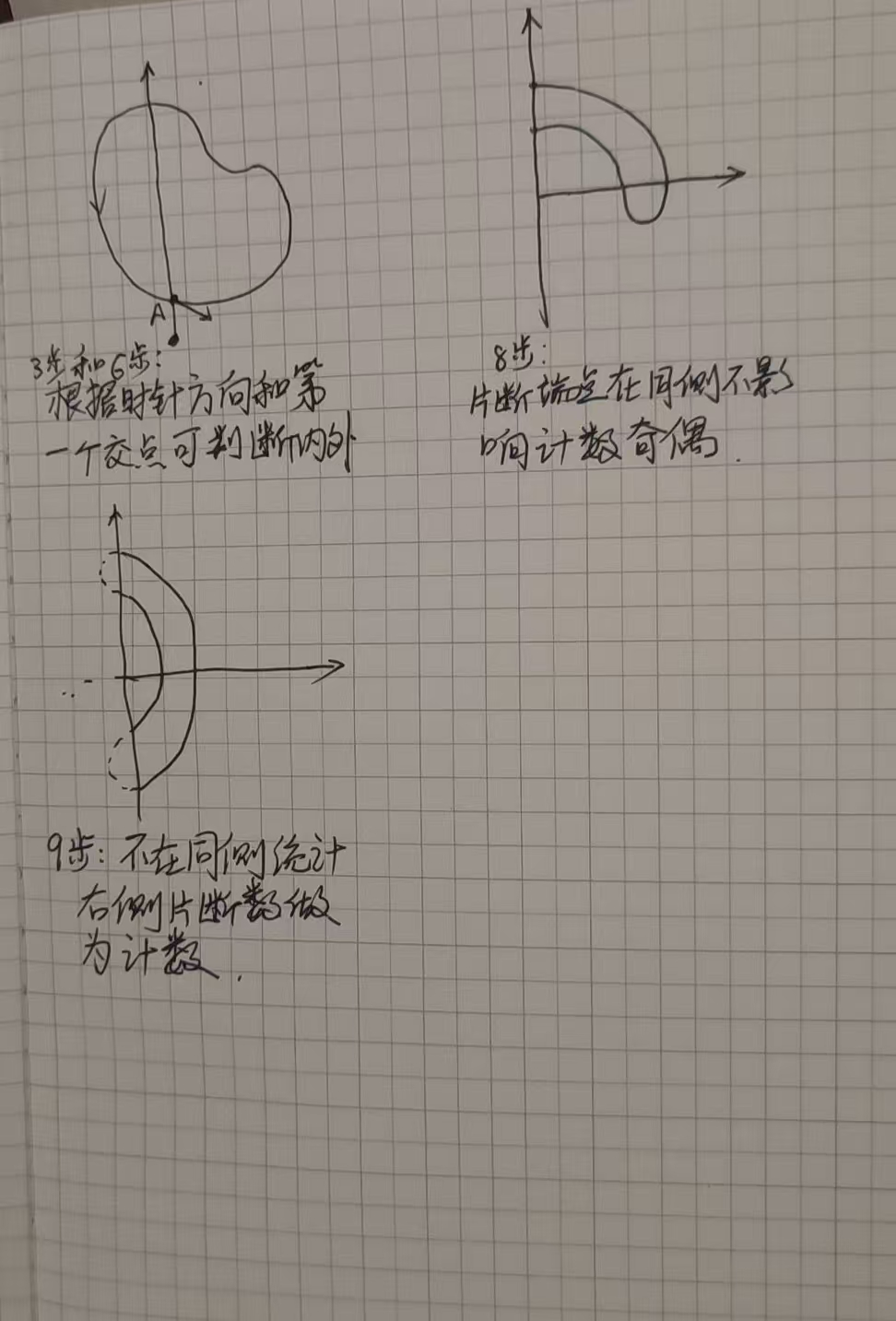
3. 如果多邊形有順逆時針方向，根據第一個交點的穿過形式和可信度判斷內外，可信度滿足要求直接返回結果。

4. y軸負方向做射線，計算所有交點。

5. 根據交點統計計數和可信度，可信度符合要求則直接返回結果。

6. 如果多邊形有順逆時針方向，根據第一個交點的穿過形式和可信度判斷內外，可信度滿足要求直接返回結果。

7. 利用交點把多邊形打斷成片段，這些片段是被y軸正負方向射線分開的。

8. 判斷片段的兩個端點是否在x軸方向射線同側，如果在同側不影響計數，直接不用考慮。

9. 如果不在同側，統計在y軸正方向射線的右側片段數，這個片段數就是判斷內外的計數。這步可以通過采用的方式判斷是否在右側。

如下圖所示：

總結

這可能就是書本中的算法和在大廠中實際跑的算法的區別。書本中的算法追求理論可行，實際應用的算法追求實踐可行。

雖然我以前寫過好多版這個算法了，但為了寫這篇文章，我又把它實現了一遍，源碼放到星球里了。為了省時間目前只做了直線求交，但算法本身是支持曲線的。

星球中的Demo可直接調試運行，學源碼能看到很多細節，歡迎加入我們的星球，支持一下作者。現有源碼已經很值得加入了。后續算法源碼還會不斷在星球中發布。

星球地址：https://t.zsxq.com/bVB9h