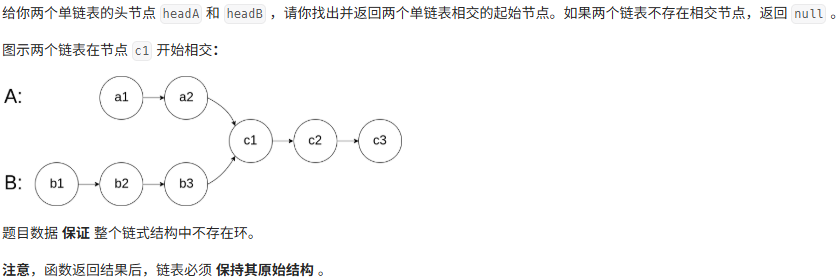
問題描述
核心思路：雙指針交替遍歷
算法思想： 使用兩個指針 pa 和 pb 分別從鏈表A和鏈表B的頭節點出發，同步向后遍歷。當任一指針走到鏈表末尾時，將其重定位到另一鏈表的頭節點繼續遍歷。若兩鏈表相交，pa 和 pb 最終會在相交節點相遇；若不相交，則最終會同時到達 null。
數學原理： 設鏈表A獨立部分長度為 a，鏈表B獨立部分長度為 b，公共部分長度為 c。
- 指針?
pa?的路徑：a + (b - c) + c = a + b - 指針?
pb?的路徑：b + (a - c) + c = a + b?兩指針走過的總長度均為?a + b，因此必然在相交節點（或?null）相遇。
代碼實現：
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {if(headA==null||headB==null){return null;}ListNode pa=headA;ListNode pb=headB;while(pa!=pb){if(pa==null){pa=headB;}else{pa=pa.next;}if(pb==null){pb=headA;}else{pb=pb.next;}}return pa;}復雜度分析：
- 時間復雜度：O(m + n)，其中 m 和 n 分別為鏈表長度。
- 空間復雜度：O(1)，僅使用兩個指針。
關鍵點：
- 循環終止條件：
pa == pb?時退出循環（包括兩者均為?null?的情況）。 - 重定位時機：當指針走到當前鏈表末尾時，立即切換到另一鏈表的頭部。
- 不相交處理：兩指針最終同時為?
null，返回?null?符合預期。
其他解法對比
方法二：計算長度差（同步遍歷）
思路：
- 遍歷兩鏈表，分別計算長度?
lenA?和?lenB。 - 長鏈表指針先走?
|lenA - lenB|?步。 - 兩指針同步遍歷，相遇點即為相交節點。
代碼：
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {int lenA = getLength(headA), lenB = getLength(headB);ListNode pa = headA, pb = headB;// 長鏈表指針先走差值步if (lenA > lenB) {for (int i = 0; i < lenA - lenB; i++) pa = pa.nextB; i++) pa = pa.next;} else {for (int i = 0; i < lenB - lenA; i++) pb = pb.next;}// 同步遍歷直至相遇while (pa != pb) {pa = pa.next;pb = pb.next;}return pa;
}private int getLength(ListNode head) {int lenLength(ListNode head) {int len = 0;while (head != null) {len++;head = head.next;}return len;
}復雜度：
- 時間復雜度：O(m + n)（需兩次遍歷）。
- 空間復雜度：O(1)。
適用場景： 當鏈表長度差異較大時，此方法可能略快于雙指針交替法。
方法三：哈希集合（空間換時間）
思路： 1時間） 思路：
- 遍歷鏈表A，將所有節點存入?
HashSet。 - 遍歷鏈表B，檢查節點是否在集合中，第一個存在的節點即為交點。
代碼：
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {Set<ListNode> set = new HashSet<>();while (headA != null) {set.add(headA);headA = headA.next;}while (headB != null) {if (set.contains(headB)) return headB;headB = headB.next;}return null;
}復雜度：
- 時間復雜度：O(m + n)。
- 空間復雜度：O(m)（存儲鏈表A的節點）。
適用場景： 對空間復雜度不敏感時，代碼最簡潔直觀。
方法對比總結
| 方法 | 時間復雜度 | 空間復雜度 | 特點 |
|---|---|---|---|
| 雙指針交替遍歷 | O(m + n) | O(1) | 空間最優，代碼簡潔 |
| 計算長度差 | O(m + n) | O(1) | 邏輯清晰，略多一次遍歷 |
| 哈希集合 | O(m + n) | O(m) | 思路直接，但需額外空間 |
推薦：雙指針交替遍歷法在空間和代碼簡潔性上表現最佳，是面試中的理想解法。
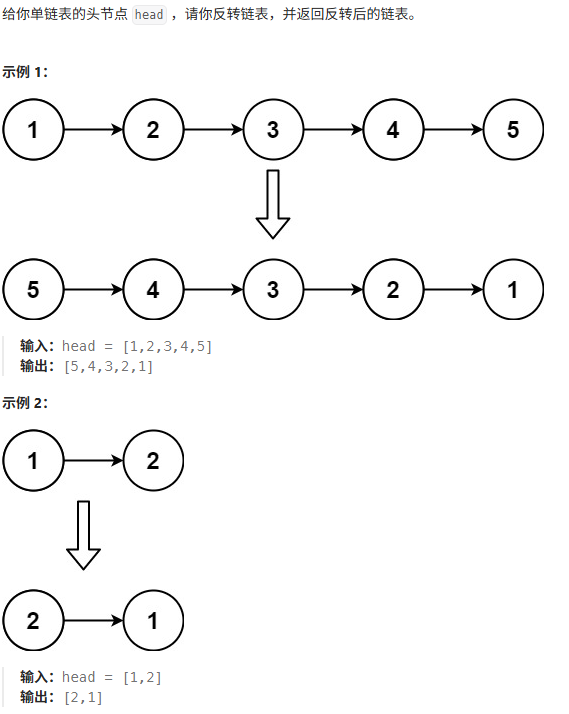
問題描述
核心解法：迭代雙指針法
算法思想： 使用雙指針 new_head 和 temp 動態反轉鏈表：
new_head：指向已反轉部分的頭節點（初始為null）temp：遍歷原鏈表的當前節點?每次迭代將當前節點從原鏈表斷開，插入到反轉鏈表的頭部，實現原地反轉。
代碼實現：
public ListNode reverseList(ListNode head) {ListNode new_head = null;ListNode temp = head;while (temp != null) {ListNode next = temp.next; // 保存后繼節點temp.next = new_head; // 當前節點指向反轉鏈表頭部new_head = temp; // 更新反轉鏈表頭temp = next; // 移動到下一個節點}return new_head;
}圖解過程：
原始鏈表：1 → 2 → 3 → 4 → null
迭代過程：
第1輪：new_head=1→null, temp=2
第2輪：new_head=2→1→null, temp=3
第3輪：new_head=3→2→1→null, temp=4
第4輪：new_head=4→3→2→1→null, temp=null復雜度分析：
- 時間復雜度：O(n)，僅需一次遍歷
- 空間復雜度：O(1)，僅使用常量空間
優勢：
- 原地操作，不占用額外空間
- 邏輯清晰，代碼簡潔
- 適用于所有編程語言的鏈表實現
其他經典解法
方法二：遞歸法（分治思想）
算法思想：
- 遞歸到鏈表尾部
- 回溯時反轉節點指向
- 返回新的頭節點
public ListNode reverseList(ListNode head) {if (head == null || head.next == null) {return head;}ListNode newHead = reverseList(head.next); // 遞歸到尾部head.next.next = head; // 反轉指針方向head.next = null; // 斷開原指針return newHead;
}復雜度分析：
- 時間復雜度：O(n)
- 空間復雜度：O(n)（遞歸棧空間）
適用場景：
- 鏈表長度適中（避免棧溢出）
- 需要簡潔的代碼表達
- 函數式編程環境
方法三：頭插法（使用虛擬節點）
算法思想：
- 創建虛擬頭節點?
dummy - 遍歷原鏈表，將每個節點插入到?
dummy?之后 - 返回?
dummy.next
public ListNode reverseList(ListNode head) {ListNode dummy = new ListNode(-1);ListNode cur = head;while (cur != null) {ListNode next = cur.next; // 保存后繼節點cur.next = dummy.next; // 頭插操作dummy.next = cur; // 更新頭節點cur = next; // 移動指針}return dummy.next;
}復雜度分析：
- 時間復雜度：O(n)
- 空間復雜度：O(1)
優勢：
- 統一處理頭節點特殊情況
- 邏輯更易理解
- 支持鏈表的其他變形操作
方法對比總結
| 方法 | 時間復雜度 | 空間復雜度 | 特點 |
|---|---|---|---|
| 迭代雙指針 | O(n) | O(1) | 空間最優，推薦首選 |
| 遞歸法 | O(n) | O(n) | 代碼簡潔，但空間消耗大 |
| 頭插法（虛擬節點） | O(n) | O(1) | 邏輯清晰，易擴展 |
核心技巧：
- 指針保存：在修改節點指針前，必須保存后繼節點引用
- 頭插操作：將節點插入鏈表頭部是反轉的關鍵
- 終止條件：注意處理空鏈表和單節點鏈表的邊界情況
延伸思考：
- 如何反轉部分鏈表（區間反轉）？
- 如何K個一組反轉鏈表？
- 如何判斷鏈表是否有環？（快慢指針技巧）
迭代雙指針法因其優異的時空復雜度，成為面試和工程實踐中的首選方案。掌握這三種經典解法，能夠靈活應對各種鏈表反轉問題。
