可解釋人工智能（XAI）方法（例如常見的XGBoost-SHAP方法）可以捕捉到非線性的關系，但這種方法忽略了地理單元之間的空間效應；而傳統的空間模型（例如常見的GWR）雖然考慮了空間效應，卻仍然是基于線性的假設。因此，為了兼顧空間效應與非線性，一種可解釋的地理人工智能（GeoXAI）方法，即顧及地理位置的機器學習回歸（GeoMLR）與GeoShapley的聯合框架，被用于探索這種復雜的關系之中。

一、Shapley類方法基本知識
想必大家對Shapley類方法（例如SHAP）有一定的興趣。在地學/空間領域，基于SHAP的研究從2022年開始暴增。
*然而，絕大多數研究仍然把它作為一個普通的全局解釋方法用于特征重要性排序和分析非線性的關系。其實，這些技術在SHAP之前就已經存在了。*
本Workshop將補充更多的Shapley相關的知識，并闡述這種局部解釋方法在地學/空間研究上的潛力。

Shapley值（Shapley Value）是合作博弈論中的核心概念，由諾貝爾經濟學獎得主Lloyd Shapley于1953年提出，用于解決多人合作博弈中公平分配聯盟總收益的問題。其核心思想是根據每個參與者對聯盟的邊際貢獻（Marginal Contribution）加權平均來確定分配方案，滿足公平性、對稱性和效率性等公理化性質。

一直以來，機器學習的可解釋性都受到廣泛關注。 現在的解釋方法分為兩類：全局解釋和局部解釋。特征重要性和偏依賴圖是一種傳統的全局解釋方法，但它并不完全利于決策支持，因為特征的影響并非是處處同質的。Shapley值的引入使得特征在*局部樣本個體和全局上的影響*都可以被量化，從而可以提供更深層次的見解。

這種局部解釋方法與地學/空間研究更加契合。

本項目來源于和鯨社區，使用轉載需要標注來源
作者: 和鯨社區
來源: 和鯨社區
0.機器學習中的Shapley值
在機器學習中，預測值??可以被以下公式描述:

眾所周知，Shapley值還包含了交互值，Shapley交互值又是什么呢？

特征m全局的影響就是所有樣本個體上Shapley值的平均值。

1.不同機器模型的Shapley值的計算方法
也許你已經發現，用Python中的SHAP庫解釋XGBoost、隨機森林很快，但是解釋SVM卻很慢，這是為什么呢？
事實上，Shapley類方法分了很多種，這些不同的解釋器都被集成進了SHAP庫中。你在調用SHAP庫解釋模型時，它使用的是不同解釋器。

Kernel SHAP (解釋一切模型)

Kernel SHAP方法由Lundberg和Lee(2017)引入進機器學習的解釋，它本質上是一種模型無關的解釋方法，也就是說，它可以解釋任何模型。但是，它的時間復雜度極大，運行時間非常緩慢，這與特征數量有關。

前面提及的解釋SVM非常慢，就是因為SVM是用Kernel SHAP進行解釋的。

Lundberg S, Lee S. A unified approach to interpreting model predictions[J]. arXiv preprint arXiv:1705.07874, 2017.

Tree SHAP (解釋基于樹的模型)

基于樹的模型（如隨機森林、XGBoost）具有的特殊結構，因此，Lundberg(2020)等提出Tree SHAP，用于近似估測基于樹的模型中特征的Shapley值。

與Kernel SHAP相比，Tree SHAP是一種模型有關的解釋方法，它只能用于基于樹的模型。但Tree SHAP的時間復雜度被大大優化，因此“基于樹的模型 + Tree SHAP”的聯合方法得到了廣泛的應用。

Lundberg S, Erion G, Chen H, et al. From local explanations to global understanding with explainable AI for trees[J]. Nature machine intelligence, 2020, 2(1): 56-67.

此外，SHAP庫中還針對其他不同的模型結構集成了DeepExplainer、GradientExplainer等解釋器

2.局部解釋方法在地學/空間研究的潛力
盡管目前許多地學/空間研究應用了機器學習+Shapley類的方法，但這些研究仍然停留在特征全局重要性和非線性偏依賴圖的全局解釋階段。事實上，這種結果不依賴Shapley值和博弈論也可以實現，這些方法在Python的SHAP庫出現之前就存在。

Shapley類方法的重點在于它的局部解釋能力，偏偏這樣的能力能很好的與地學/空間研究結合起來。

Shapley類方法可以解釋某個個體樣本中，該個體的特征是如何對該個體的預測值產生影響的。在地學/空間研究中，“個體”就是一個個“地理單元”，因此，每一個地理單元中的每一個特征發揮的作用，都可以被繪制于地圖之上，發現特征影響的空間異質性，從而為決策支持提供因地制宜的見解。 再結合非線性的偏依賴圖，就可以發現特征“非線性”且“空間非平穩性”的影響，從而提供“定量化”且“因地制宜”的決策支持。

這種局部解釋的能力使Shapley類方法在地學/空間的分析研究中產生更有意義的研究結果。

目前，已經有少部分研究已在行業頂刊上應用了這種Shapley類方法的局部解釋能力：

Ke E, Zhao J, Zhao Y. Investigating the influence of nonlinear spatial heterogeneity in urban flooding factors using geographic explainable artificial intelligence[J]. Journal of Hydrology, 2025, 648: 132398.

Luo P, Chen C, Gao S, et al. Understanding of the predictability and uncertainty in population distributions empowered by visual analytics[J]. International Journal of Geographical Information Science, 2024: 1-31.

An R, Tong Z, Tan B, et al. Revealing the relationship between 2D/3D built environment and jobs-housing separation coupling nonlinearity and spatial nonstationarity[J]. Journal of Transport Geography, 2025, 123: 104112.

3.GeoShapley方法
顧及地理空間的機器學習回歸（GeoMLR）+ GeoShapley更適用于專門的空間研究。前文提到，機器學習中的“個體”就是一個個“地理單元”，在生物或是醫學的研究中，樣本個體通常是獨立的，然而在空間研究中，地理單元間卻是存在空間關系的。

Li(2022)使用GeoMLR（在傳統特征中加入了表征空間的坐標X和Y）探索了機器學習捕捉空間關系的能力，隨后他于2024年提出了GeoShapley方法。GeoShapley方法源自Joint Shapley方法，它可以發現兩種特征的聯合貢獻。因此，GeoShapley方法用其量化特征X和Y的聯合貢獻，用于表征空間位置特征的影響。

GeoShapley方法可以量化空間位置的影響，并量化出自變量中的空間效應，這也是傳統的地理加權機器學習（GWML）+SHAP所做不到的。

另外，GeoMLR可以作為一種新方法被納入空間建模，它克服了傳統空間模型線性的假設 實現了非線性的建模，也超越了傳統的機器學習建模 顧及了地理空間在其中發揮的作用。GeoShapley的解釋也提升了其實用性。

因此，在空間自相關性較高的地學/空間研究中，可以嘗試使用GeoMLR+GeoShapley方法進行分析，它可以比傳統的ML+Shapley方法提供更多在空間上的見解。

誠然，GeoShapley方法也存在缺陷。GeoShapley方法是一種模型無關的方法，它是基于Kernel SHAP開發的，因此它的時間復雜度極高，運行時間非常久。

Li Z. Extracting spatial effects from machine learning model using local interpretation method: An example of SHAP and XGBoost[J]. Computers, Environment and Urban Systems, 2022, 96: 101845.

Li Z. GeoShapley: A Game Theory Approach to Measuring Spatial Effects in Machine Learning Models[J]. Annals of the American Association of Geographers, 2024: 1-21.

二、Workshop實驗框架與數據
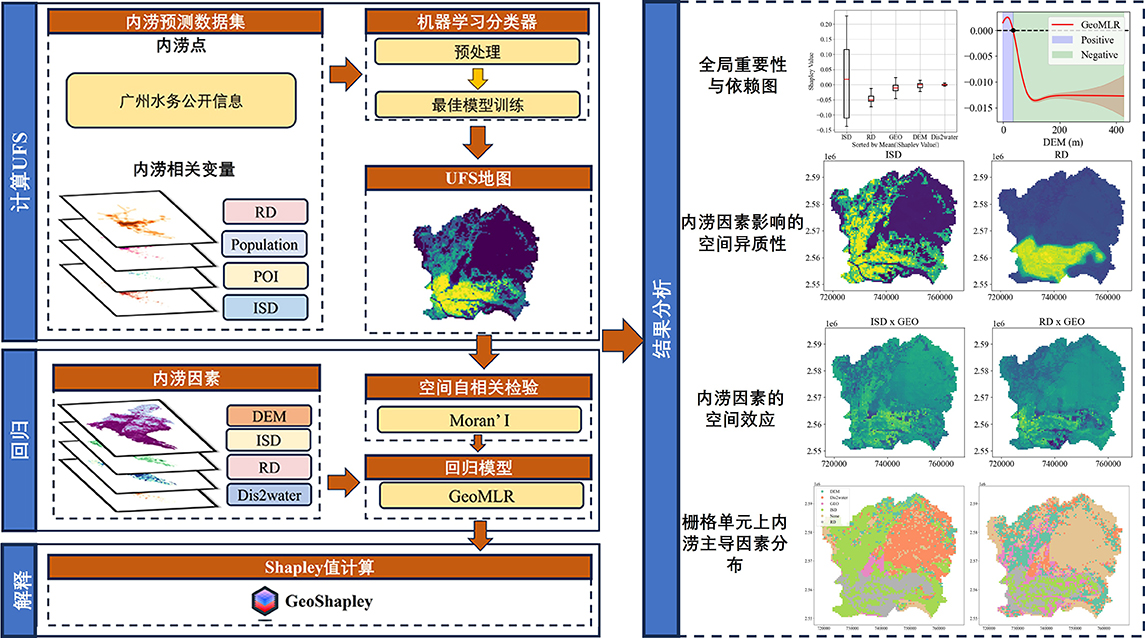
本次Workshop的內容分為三部分（計算UFS-用因素擬合UFS-解釋擬合結果）：

基于機器學習分類器計算城市內澇易發性（UFS）。使用內澇相關的變量道路密度（RD）、人口數量（POP）、興趣點（POI）、不透水面密度（ISD）與內澇點訓練XGBoost分類器，從而預測所有地理單元內澇發生的概率（即城市內澇易發性UFS）。

使用內澇因素和GeoMLR擬合UFS。使用內澇因素高程（DEM）、ISD、RD、到達水體距離（Dis2water）、地理坐標特征X、Y，和分類器輸出的UFS，基于XGBoost進行回歸。

使用GeoShapley解釋分析。使用Shapley值解釋內澇因素、地理空間變量的影響，繪制內澇因素全局影響圖、內澇因素空間異質的影響圖、非線性依賴圖、內澇因素的空間交互圖、柵格尺度上內澇的主導因素圖。

廣州市主城區的漁網數據，Shp格式。網格為500*500m。數據包含了['Shape_Leng', 'Shape_Area', 'DEM', 'Dis2water', 'ISD', 'POI', 'RD', 'POP', 'X', 'Y']字段。數據時間為2020年，數據全部提取自公開的數據。其中，'Shape_Leng'代表網格的周長；'Shape_Area'代表網格的面積；'X'和'Y'分別代表WGS 1984 UTM Zone 49N下每個網格的橫縱坐標。

內澇數據集，csv格式。里面包含75個正樣本和75個負樣本。數據集包含['ID','Flood','POI','POP','RD','ISD']字段。數據時間為2020年，數據全部提取自公開的數據。其中，'ID'代表樣本ID；'Flood'代表是否發生過內澇，1為是，0為否。

為什么不在訓練分類器的時候就把坐標X和Y作為特征輸入進去呢？

把X和Y作為特征輸入進去，那么訓練得到的模型泛化能力豈不是很弱？

內澇相關變量和內澇因素有什么區別？

這個UFS到底是什么？為什么用了兩個機器學習模型？

在計算UFS的機器學習分類器和回歸分析的GeoMLR中，都使用了不透水面密度（ISD）和道路密度（RD）這兩個變量，這沒有問題嗎？

為什么Workshop中的內澇因素那么少？

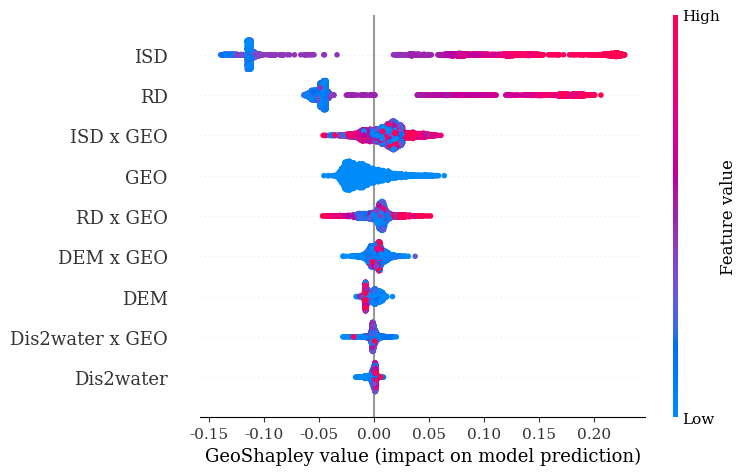
其中，GEO代表著地理位置特征X和Y共同做出的影響，即空間位置對UFS的影響。

內澇因素xGEO則代表了內澇因素的空間效應

geomlr_rslt.partial_dependence_plots(figsize=(10,6),max_cols=2,gam_curve=True)

解釋分為全局解釋和局部解釋兩種。
接下來，我們首先從全局的視角對解釋結果進行分析

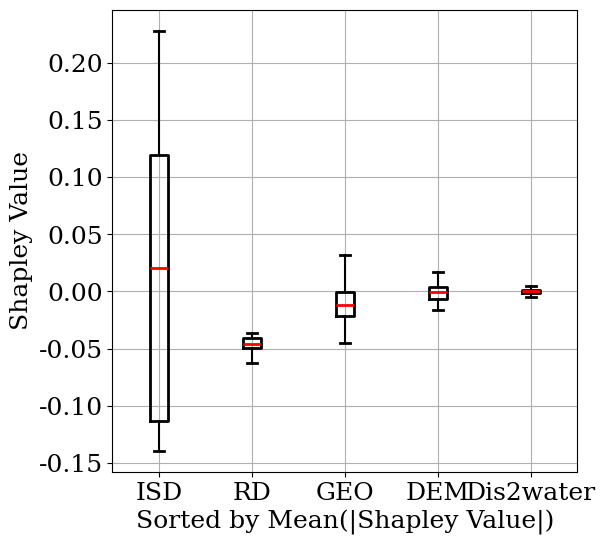
3.全局重要性
繪制全局重要性的箱線圖。

某一特征的 所有shapley值的絕對值的平均值（Mean(|Shapley Value|)） 就是該特征的全局重要性。

在橫軸上，從左到右排列全局重要性從高到低的特征。

箱線圖則展現了Shapley值的數據分布。也可以看出對UFS影響最大的因素是ISD和RD。

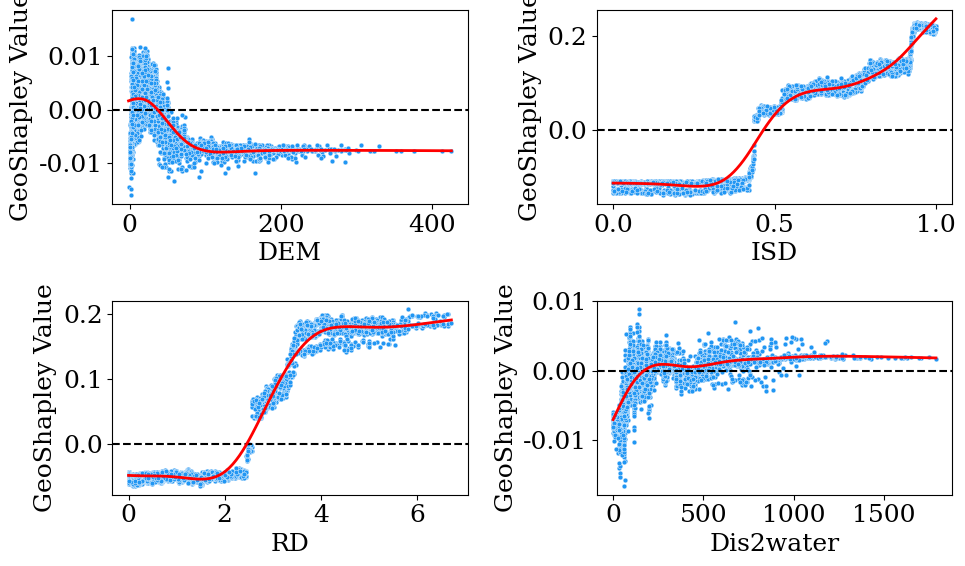
4.非線性偏依賴圖
這一步的目的是繪制偏依賴圖，發現內澇因素與UFS之間的非線性關系。

本質上，偏依賴圖也還是是一種全局解釋方法。

fig, axes = plt.subplots(2, 2, figsize=(10, 8), dpi=100)
plt.subplots_adjust(wspace=0.4, hspace=0.3)  # 調整子圖間隙units_list = [' (m)', '', ' (m/m2)', ' (m)']for i, name in enumerate(['DEM', 'ISD', 'RD', 'Dis2water']):row = i // 2col = i % 2# 基礎設置axes[row, col].set_xlabel(name + units_list[i])axes[row, col].set_ylabel(f'Shapley value for {name}')axes[row, col].axhline(y=0, color='black', linestyle='--', linewidth=2)# 擬合GAM模型lam = np.logspace(2, 7, 5).reshape(-1, 1)gam = pygam.LinearGAM(pygam.s(0), fit_intercept=False).gridsearch(var.loc[:, name].values.reshape(-1, 1), shapley.loc[:, name].values.reshape(-1, 1), lam=lam)# 繪制偏依賴圖for term in gam.terms:XX = gam.generate_X_grid(term=0)pdep, confi = gam.partial_dependence(term=0, X=XX, width=0.95) #95%的置信區間# 繪制曲線和置信區間axes[row, col].plot(XX, pdep, color="red", lw=2)axes[row, col].fill_between(XX[:, 0], confi[:, 0], confi[:, 1], color="red", alpha=0.2)# 找交點邏輯# 1. 找到與y=0的交點sign_changes = np.where(np.diff(np.sign(pdep).flatten()))[0]x0_list = []# 遍歷所有符號變化點for idx in sign_changes:# 跳過區間端點if idx == 0 or idx == len(XX)-1:continue# 線性插值求精確交點x1, x2 = XX[idx][0], XX[idx+1][0]y1, y2 = pdep[idx], pdep[idx+1]x0 = x1 - y1*(x2-x1)/(y2-y1)x0_list.append(x0)# 判斷填充顏色if y1 > 0:  # 左側高于0left_color = "blue"right_color = "green"else:       # 左側低于0left_color = "green"right_color = "blue"xmin, xmax = XX[:,0].min(), XX[:,0].max()axes[row, col].axvspan(xmin, x0, alpha=0.2, color=left_color)axes[row, col].axvspan(x0, xmax, alpha=0.2, color=right_color)axes[row, col].scatter(x0, 0, s=50, color='black', zorder=5)# 圖例設置（只在第一個子圖添加）if i == 0:legend_elements = [Line2D([0], [0], color='red', lw=2, label='GeoMLR'),Patch(facecolor='blue', alpha=0.2, label='Positive'),Patch(facecolor='green', alpha=0.2, label='Negative'),]axes[row, col].legend(handles=legend_elements, loc='upper right')plt.show()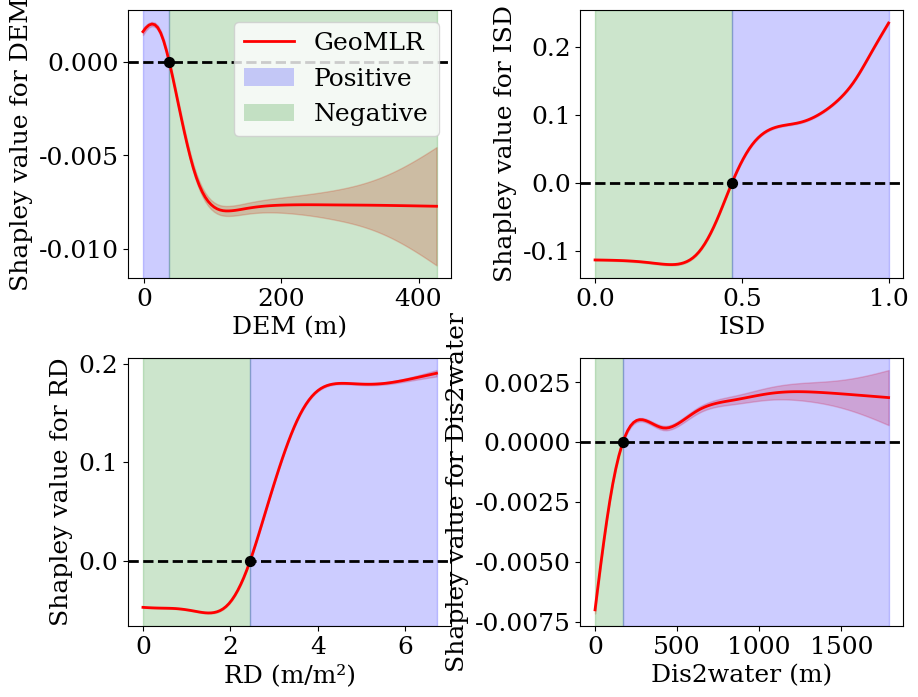

從依賴圖中可以看出，將ISD控制在0.5以下，將RD控制在2.5m/m2以下有助于控制廣州主城區的UFS。

關于Shapley類方法

Shapley類方法的局部解釋能力，有助于理解自變量x對因變量y的影響，尤其是理解影響的空間異質性；
GeoMLR+GeoShapley不僅仍然有這種局部解釋能力，它還考慮了空間的貢獻，并且能揭示出空間效應。這是現今的地理加權機器學習（GWML）+SHAP方法做不到的。它更適用于空間建模，更適用于研究空間效應；
GeoShapley也存在缺陷，它是基于Kernel SHAP開發的，它的時間復雜度高，運行時間久。