論文Review 3DGS PGSR | TVCG2024 ZJU-3DV | 幾何約束的3DGS表面重建

基本信息

題目：PGSR: Planar-based Gaussian Splatting for Efficient ?and High-Fidelity Surface Reconstruction

來源：TVCG2024

學校：ZJU-3DV

是否開源：https://github.com/zju3dv/PGSR

摘要：3DGS表面重建

????????最近，3D高斯拋雪球( 3DGS )由于其高質量的渲染效果以及超快的訓練和渲染速度引起了廣泛的關注。然而，由于高斯點云的非結構化和不規則性，單純依靠圖像重建損失難以保證幾何重建精度和多視圖一致性。盡管最近出現了許多基于3DGS的曲面重建研究，但其網格質量普遍不盡人意。為了解決這個問題，我們提出了一種快速的基于平面的高斯散點重建表示( PGSR )，在保證高質量渲染的同時實現了高保真的表面重建。具體來說，我們首先介紹一種無偏深度渲染方法，該方法基于點云的高斯分布直接繪制相機原點到高斯平面的距離和對應的法線圖，并將兩者相除得到無偏深度。然后我們介紹了單視圖幾何，多視圖photometric和幾何正則化以保持全局幾何精度。我們還提出了一種相機曝光補償模型來應對光照變化較大的場景。在室內和室外場景上的實驗表明，該方法在保持高保真渲染和幾何重建的同時，實現了快速的訓練和渲染，優于基于3DGS和NeRF的方法。

Introduction

????????論文針對新型視圖合成（Novel View Synthesis）和幾何重建（Geometry Reconstruction）問題，這些在AR/VR、3D內容生成和自動駕駛中至關重要。傳統NeRF（Neural Radiance Fields）方法渲染質量高但訓練和渲染慢（需數小時至數百小時）。3DGS通過顯式3D高斯點云實現分鐘級訓練和毫秒級渲染，但高斯點云的無結構性和不規則性導致幾何重建精度差，無法保證多視圖一致性。

問題與挑戰：

3DGS僅依賴圖像重建損失，易陷入局部最優，高斯無法貼合真實表面。
現有3DGS-based表面重建（如SuGaR）網格質量差，無法提取平滑表面。
需要在保持渲染質量和速度的同時，提升幾何精度。

主要貢獻：

提出無偏深度渲染方法：將3D高斯壓縮為平面，渲染平面參數（距離和法線），轉換為無偏深度，促進幾何約束引入。
引入單視圖和多視圖正則化：優化每個像素的平面參數，實現全局幾何一致性。
曝光補償模型：處理光照變化大的場景，提升重建精度。
實驗證明：在保持3DGS渲染質量和速度的前提下，實現SOTA幾何重建精度，訓練時間比NeRF-based方法快100倍。

方法概述如圖4所示：壓縮高斯為平面，渲染距離/法線/深度圖；引入幾何和光度正則化；曝光補償RGB損失。

Related Works

論文回顧了表面重建的歷史，從傳統方法到神經方法，再到基于高斯的最新進展。

傳統表面重建：

基于點云、體素或深度圖的多視圖立體（MVS）Pipeline。【時間太久遠的文獻就不寫出來了】
使用塊匹配【PatchMatch】提取稠密點云，然后三角化或隱式表面擬合。
缺點：易受噪聲影響，后續方法（如[PatchMatchNet]）整合深度網絡提升匹配精度。

神經表面重建：

早期端到端方法使用點云、體素或網格/隱式場，但計算開銷大，需要大量標注數據。
NeRF-based方法通過體渲染實現高保真視圖合成，但表面捕捉差。
改進：引入占用場或符號距離場（SDF）；分解場景為點（如[Point-NeRF]）或體素（如[Vox-surf,Neuralangelo），減少MLP依賴。
缺點：訓練慢（需數天，多GPU）。

基于3DGS的表面重建：

SuGaR ：從3DGS提取網格，通過正則化鼓勵高斯貼合表面，從密度場采樣點云，用Poisson重建網格。但依賴偏置深度，表面不平滑。
同期工作：2DGS 將3D高斯壓縮為2D盤，實現多視圖一致幾何；GOF 形成高斯不透明場，從水平集提取幾何。
缺點：這些方法深度不精確，多視圖一致性差。PGSR通過平面渲染和正則化解決這些問題。

III. PRELIMINARY OF 3D GAUSSIAN SPLATTING

3DGS的基礎知識，總結的很好，就放在這了。

Method

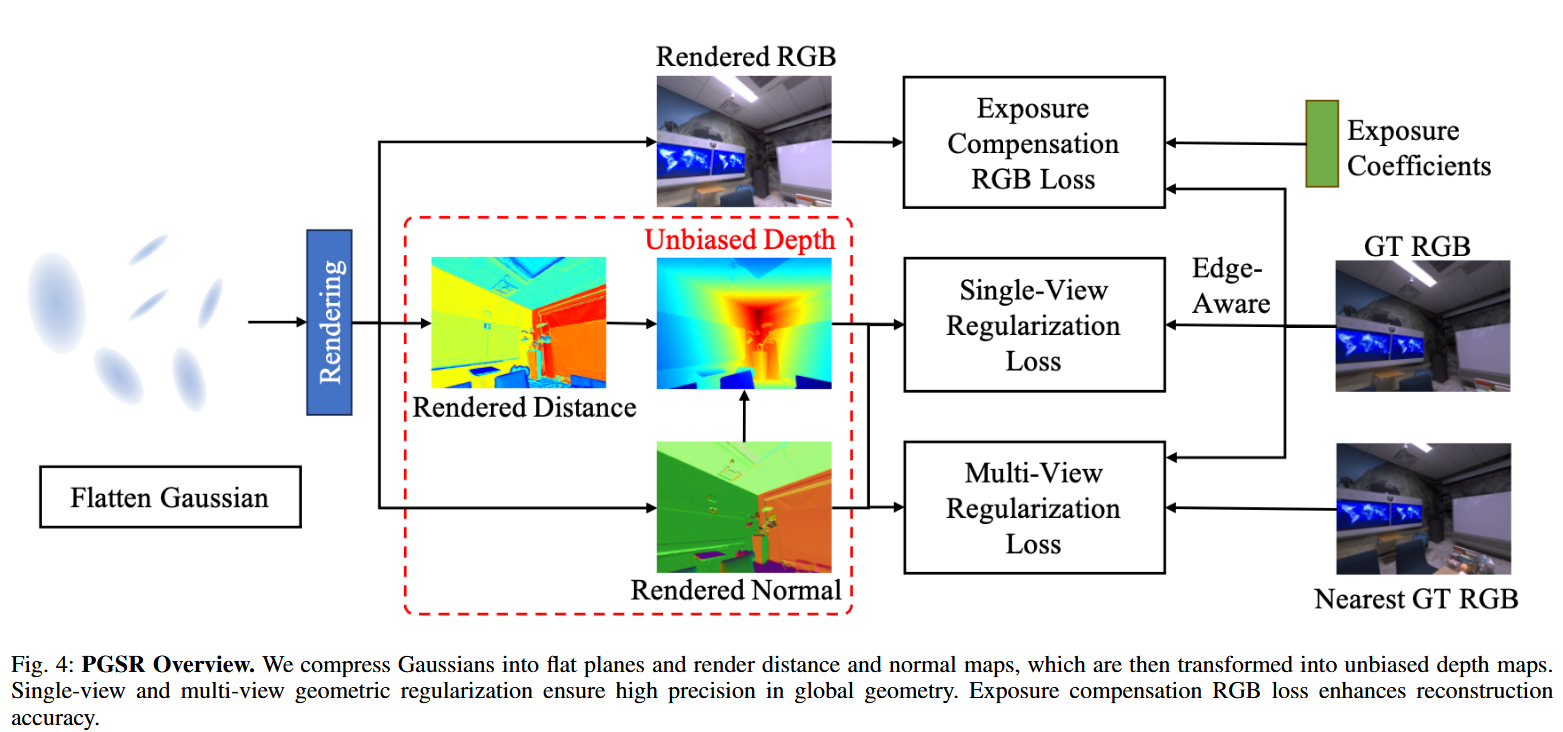
A. Planar-based Gaussian Splatting Representation

關鍵概念：

傳統3DGS使用3D高斯橢球體表示場景，但難以精確建模幾何屬性（如深度和法向量），因為橢球體形狀不貼合實際表面。
解決方案：將3D高斯“扁平化”（flatten）為2D平面高斯，使其更好地擬合場景表面。平面高斯近似局部平面，便于渲染深度和法向量。
優勢：渲染的深度與平面形狀一致，避免幾何沖突；消除權重累積影響，實現無偏深度（見Fig. 6）。

Flattening 3D Gaussian（扁平化3D高斯）：

[9] Hanlin Chen, Chen Li, and Gim Hee Lee. Neusg: Neural implicit surface reconstruction with 3d gaussian splatting guidance. arXiv preprint arXiv:2312.00846, 2023.

Unbiased Depth Rendering（無偏深度渲染）：

B. Geometric Regularization

這一節引入幾何正則化，確保3D高斯貼合實際表面。分為單視圖和多視圖正則化。

1) Single-View Regularization（單視圖正則化）：

[24] Yingwenqi Jiang, Jiadong Tu, Yuan Liu, Xifeng Gao, Xiaoxiao Long, Wenping Wang, and Yuexin Ma. GaussianShader: 3D Gaussian Splatting with Shading Functions for Reflective Surfaces. arXiv preprint arXiv:2311.17977, 2023.

[37] Xiaoxiao Long, Yuhang Zheng, Yupeng Zheng, Beiwen Tian, Cheng Lin, Lingjie Liu, Hao Zhao, Guyue Zhou, and Wenping Wang. Adaptive Surface Normal Constraint for Geometric Estimation from Monocular Images. arXiv preprint arXiv:2402.05869, 2024.

[50] Xiaojuan Qi, Renjie Liao, Zhengzhe Liu, Raquel Urtasun, and Jiaya Jia. Geonet: Geometric neural network for joint depth and surface normal estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 283–291, 2018.

2) Multi-View Regularization（多視圖正則化）：

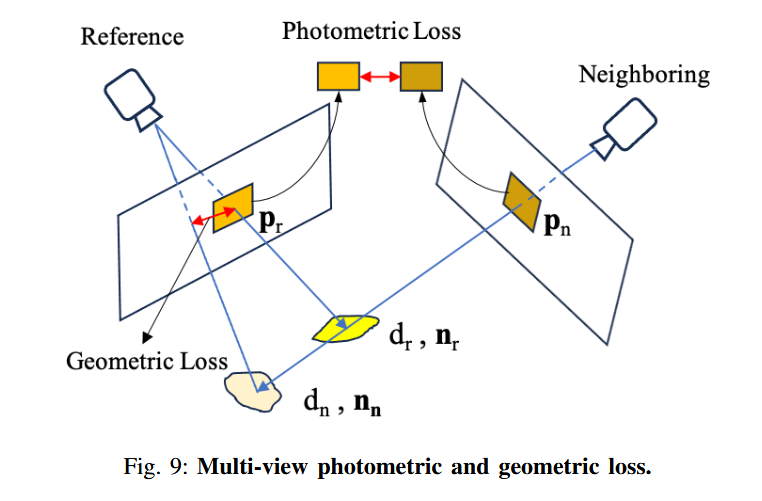
[4] Neill DF Campbell, George Vogiatzis, Carlos Herna ?ndez, and Roberto Cipolla. Using multiple hypotheses to improve depth-maps for multiview stereo. In Computer Vision–ECCV 2008: 10th European Conference on Computer Vision, Marseille, France, October 12-18, 2008, Proceedings, Part I 10, pages 766–779. Springer, 2008.

[15] Qiancheng Fu, Qingshan Xu, Yew Soon Ong, and Wenbing Tao. Geoneus: Geometry-consistent neural implicit surfaces learning for multiview reconstruction. Advances in Neural Information Processing Systems, 35:3403–3416, 2022.

[52] Johannes L Schonberger and Jan-Michael Frahm. Structure-from-motion revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4104–4113, 2016.

3) Geometric Regularization Loss（幾何正則化損失）：

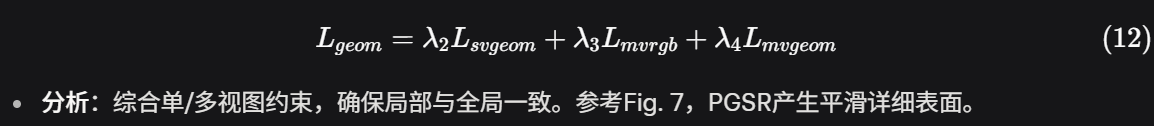
C. Exposure Compensation Image Loss

D. Training

整體方法評價：

創新：無偏深度渲染解決傳統3DGS幾何沖突；多層次正則化實現全局一致；曝光補償提升實際場景魯棒性。
潛在局限：依賴高質量位姿；計算開銷可能高于純3DGS（多視圖計算）。
與參考文獻關聯：構建于3DGS基礎上，融入MVS、NeRF元素（如Eikonal損失提及但未用）。實驗（Fig. 7）顯示優于基線。

實驗

硬件平臺

????????所有實驗在NVIDIA RTX 4090 GPU上運行，訓練迭代次數固定為30,000次，使用AbsGS的致密化策略，并采用TSDF Fusion算法從渲染深度生成網格。

數據集

數據集：
- Mip-NeRF360 ：用于評估新視圖合成性能，包含室內外復雜場景。
- DTU ：15個物體中心場景，用于評估重建質量。
- TnT [28]：大型復雜場景，用于評估重建質量。
評估標準：
- 渲染質量：PSNR（峰值信噪比，↑越高越好）、SSIM（結構相似性指數，↑越高越好）、LPIPS（學習感知圖像補丁相似性，↓越低越好）。
- 表面質量：F1分數（↑越高越好）和Chamfer距離（↓越低越好）。

[28] Arno Knapitsch, Jaesik Park, Qian-Yi Zhou, and Vladlen Koltun. Tanks and temples: Benchmarking large-scale scene reconstruction. ACM Transactions on Graphics (ToG), 36(4):1–13, 2017.

Benchmark

[20] Peter Hedman, Julien Philip, True Price, Jan-Michael Frahm, George Drettakis, and Gabriel Brostow. Deep blending for free-viewpoint imagebased rendering. ACM Transactions on Graphics (ToG), 37(6):1–15, 2018.

[45] Thomas M ?uller, Alex Evans, Christoph Schied, and Alexander Keller. Instant neural graphics primitives with a multiresolution hash encoding. ACM transactions on graphics (TOG), 41(4):1–15, 2022.

[2] Jonathan T Barron, Ben Mildenhall, Matthew Tancik, Peter Hedman, Ricardo Martin-Brualla, and Pratul P Srinivasan. Mip-NeRF: A multiscale representation for anti-aliasing neural radiance fields. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 5855–5864, 2021.

[57] Peng Wang, Lingjie Liu, Yuan Liu, Christian Theobalt, Taku Komura, and Wenping Wang. Neus: Learning neural implicit surfaces by volume rendering for multi-view reconstruction. arXiv preprint arXiv:2106.10689, 2021.

A. Real-time Rendering（實時渲染）

這一部分在Mip-NeRF360數據集上驗證渲染質量，與純新視圖合成方法（如NeRF 、Deep Blending [20]、INGP [45]、Mip-NeRF360 [2]、NeuS [57]）和類似重建方法（如3DGS 、SuGaR 、2DGS 、GOF ）比較。

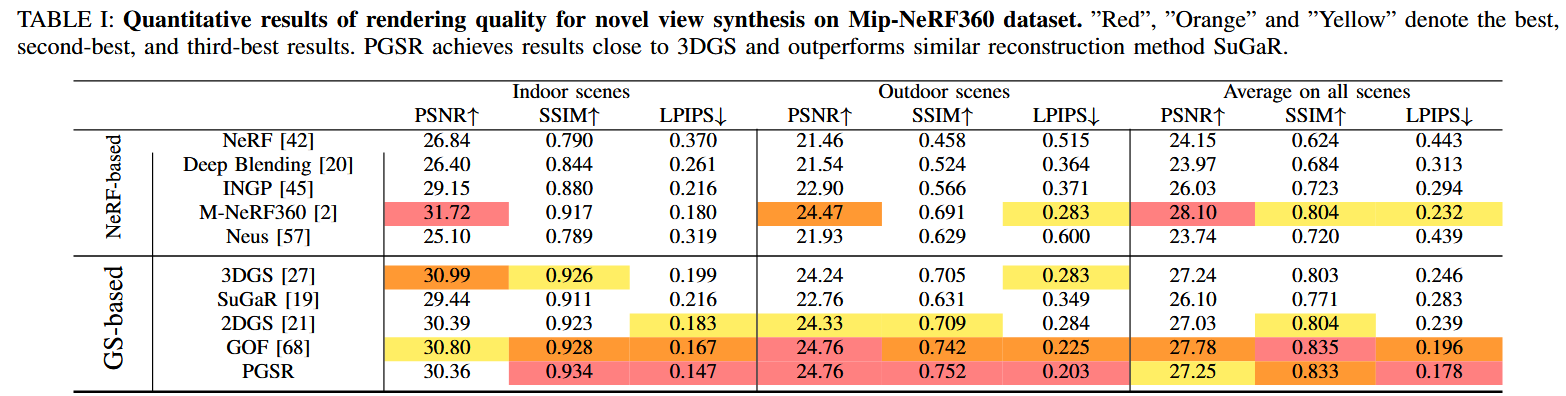
定量結果（Table I）：
- 室內場景：PGSR的PSNR為30.41、SSIM為0.930、LPIPS為0.161。相比3DGS (PSNR 30.99, SSIM 0.926, LPIPS 0.199)，PGSR在SSIM和LPIPS上略優，但PSNR稍低；優于SuGaR (PSNR 29.44, SSIM 0.911, LPIPS 0.216)和2DGS (PSNR 30.39, SSIM 0.923, LPIPS 0.183)；接近GOF (PSNR 30.80, SSIM 0.928, LPIPS 0.167)。
- 室外場景：PGSR的PSNR為24.45、SSIM為0.730、LPIPS為0.224。優于3DGS (PSNR 24.24, SSIM 0.705, LPIPS 0.283)、SuGaR (PSNR 22.76, SSIM 0.631, LPIPS 0.349)和2DGS (PSNR 24.33, SSIM 0.709, LPIPS 0.284)；略遜于GOF (PSNR 24.76, SSIM 0.742, LPIPS 0.225)。
- 所有場景平均：PGSR的PSNR為27.43、SSIM為0.830、LPIPS為0.193。整體優于3DGS (PSNR 27.24, SSIM 0.803, LPIPS 0.246)、SuGaR (PSNR 26.10, SSIM 0.771, LPIPS 0.283)和2DGS (PSNR 27.03, SSIM 0.804, LPIPS 0.239)；略遜于GOF (PSNR 27.78, SSIM 0.835, LPIPS 0.196)。
- 分析：PGSR在渲染質量上接近SOTA方法，同時提供優秀的表面重建。表中用紅色、橙色、黃色標記最佳、次佳和第三佳結果，PGSR在多個指標上排名前列。
定性結果（Fig. 5）：展示了Mip-NeRF360上的渲染比較。PGSR的表面重建更平滑、細節更豐富，與GOF類似，但優于3DGS和SuGaR（后者存在浮動偽影）。

總體而言，PGSR實現了高保真渲染，同時保持表面重建優勢。

B. Reconstruction（重建）

在DTU和TnT數據集上與神經表面重建方法（如NeuS [57]、Geo-NeuS [15]、VolSDF [61]、NeuralAngelo [33]）和3DGS-based方法（如SuGaR、2DGS、GOF）比較。

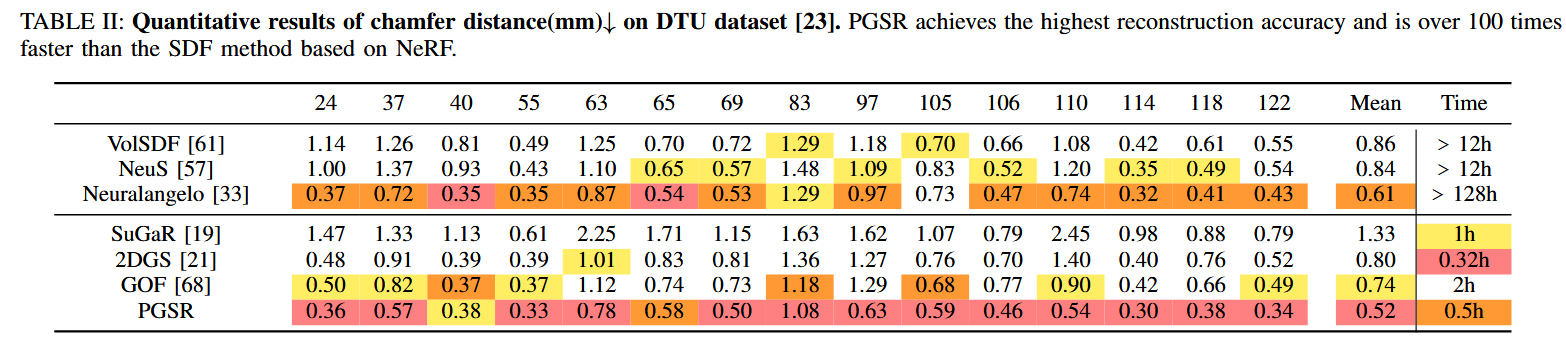
DTU數據集（Table II）：
- Chamfer距離（mm，↓）：PGSR平均為0.49（全分辨率）、0.53（下采樣DS版本）。優于NeuralAngelo (0.61)、GOF (0.74)、2DGS (0.80)、NeuS (0.84)、VolSDF (0.86)、SuGaR (1.33)。
- 訓練時間：PGSR為1.0小時（DS為0.6小時），遠快于NeuralAngelo (>128小時)和NeuS/VolSDF (>12小時)；略慢于2DGS (0.32小時)，但精度更高。
- 具體場景：在scan24、37、40等15個場景中，PGSR在多數場景（如scan24: 0.36）取得最低Chamfer距離，表明重建精度最高。
- 分析：PGSR實現了最高重建精度和相對快速訓練。Fig. 7展示了定性比較：PGSR表面更平滑、細節更豐富（如物體邊緣），優于SuGaR（粗糙）和2DGS（不完整）。
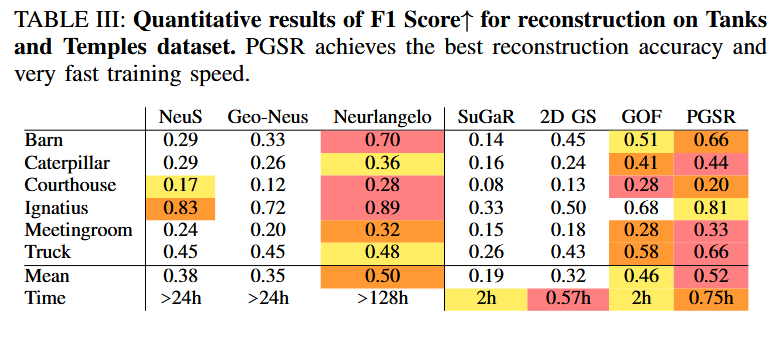
TnT數據集（Table III）：
- F1分數（↑）：PGSR平均為0.68。接近NeuralAngelo (0.70)，優于GOF (0.66)、2DGS (0.65)、SuGaR (0.62)、NeuS (0.55)等。
- Chamfer距離（↓）：PGSR平均為1.25。優于SuGaR (1.85)、2DGS (1.45)，接近GOF (1.20)和NeuralAngelo (1.15)。
- 訓練時間：PGSR為1.0小時，遠快于NeuralAngelo (>100小時)。
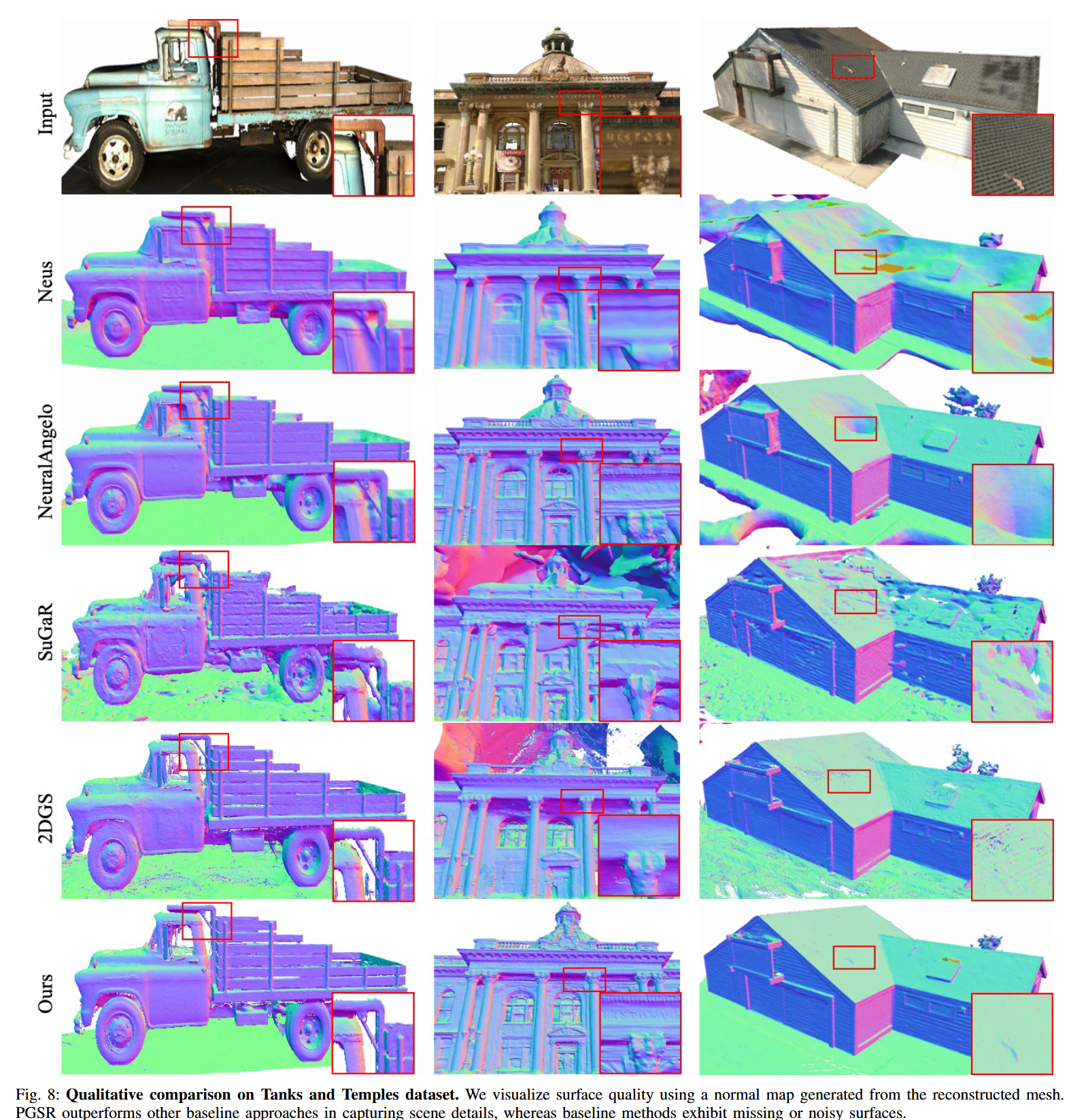
- 分析：PGSR的F1分數與NeuralAngelo相似，但訓練速度快100倍以上，且重建更多表面細節。Fig. 8展示了TnT上的定性結果：PGSR在復雜場景（如建筑物）中產生更完整的幾何結構，減少了噪點和空洞。