前言:對我來說,最有用的就是物理了,尤其是電磁學。但是要學好它,我得夯實我的基礎,前面更加基礎的數學和物理都不能拉下。現在我問了Deepseek推薦的國外物理書,這本《概念物理》是最適合我,等入門后再看《費曼物理學講義》。就這么愉快的決定了。
由于我讀的是英文版,本人水平一般,我會借助翻譯工具,所以措辭不嚴謹還請見諒。
一、關于科學
1.1?科學的測量
測量是優秀科學的標志。你對某件事了解多少,往往與你能多好地衡量它有關。著名物理學家開爾文勛爵(Lord Kelvin)在19世紀說得很好:“我經常說,當你能測量某樣東西并用數字來表達它時,你就對它有所了解了。”當你不能測量它,當你不能用數字表達它時,你的知識是貧乏的,不能令人滿意的。這也許是知識的開端,但是不管科學是什么,你的思想還沒有發展到科學的階段呢。”科學測量并不是什么新鮮事物,它可以追溯到古代。例如,在公元前3世紀,對地球、月球和太陽的大小以及它們之間的距離進行了相當精確的測量。
(應該說的是,要會定量吧)
1.1.1 埃拉托色尼如何測量地球的大小
大約公元前235年,埃拉托色尼在埃及首次測量了地球的大小。他用下面的方法計算了地球的周長。他知道太陽在夏至那天的中午是最高的(夏至在今天的日歷上大約是6月21日)。此時,垂直的樹枝投射出的影子最短。如果太陽正對著頭頂,豎著的棍子根本不會投下陰影。埃拉托色尼從圖書館的資料中得知,夏至當天正午時分,太陽正直射亞歷山大以南的城市Syene(阿斯旺大壩的所在地)。在這個特殊的時刻,陽光直接照射到Syene的一口深井里,然后又被反射回來。埃拉托色尼推斷,如果太陽光線在這一點延伸到地球上,它們將穿過地球的中心。同樣,一條從亞歷山大延伸到地球的垂直線(或其他任何地方)也會穿過地球的中心。
注意:只有在赤道附近,太陽才會在正午直射。站在赤道的陽光下,你在正午沒有投下陰影。在離赤道較遠的地方,正午時太陽不會直射在頭頂。你站得離赤道越遠,你身體投下的影子就越長。
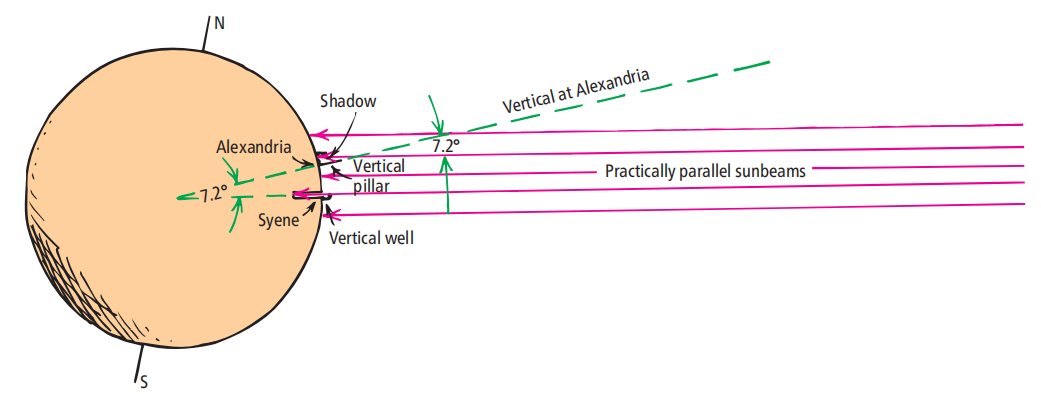
當太陽直接在Syene的頭頂上時,亞歷山大的陽光與垂直方向成7.2°角。這兩個地點的垂線都延伸到地球的中心,在那里它們形成了相同的7.2°角。
在夏至的中午,埃拉托色尼在亞歷山大測得太陽光與一根垂直的柱子之間的夾角為7.2°(圖1.1)。
360度的地球周長由多少個7.2度的段組成?答案是360°/7.2°= 50。因為7.2°是一個完整圓的1/50,埃拉托色尼推斷亞歷山大和Syene之間的距離是地球周長的1/50。
這樣地球的周長就變成了這兩個城市之間距離的50倍。
這段距離相當平坦,經常有人走過,測量員測量的距離約為5000體育場(800公里)。因此埃拉托色尼計算出地球的周長為50 * 5000體育場= 250000體育場。以公里為單位,地球的周長= 50x800km = 40000km,非常接近目前公認的地球周長值。
1.1.2 檢測點
如果同樣的7.2°指向500公里(而不是800公里),那么測量地球的周長會更小、更大還是相同?
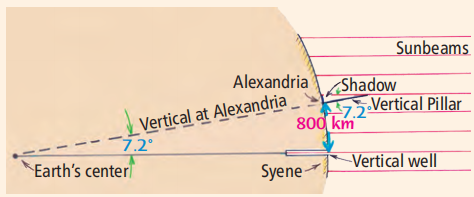
用數學方法計算,圓心角n所對的弧長
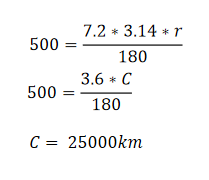
25000 < 40000,所以地球的周長會更小。
1.1.3 檢查答案
更小,因為地球的周長是50*500公里= 25000公里。在埃拉托色尼死后1700年,克里斯托弗·哥倫布在啟程前往東印度群島之前研究了埃拉托色尼的發現。然而,哥倫布沒有留心埃拉托色尼的發現,而是選擇了接受最新的地圖,這些地圖表明地球的周長比原來小了三分之一。如果哥倫布接受埃拉托色尼所說的更大的周長,那么他就會知道他沒有在中國或東印度群島登陸,而是在加勒比海登陸。
1.1.4 物理練習
通過樹/旗桿陰影測地球的大小
在測量地球的大小時,埃拉托色尼考慮了兩個南北位置,它們非常靠近一條特定的經線。這不是必要的。經線是許多大圓中的一個。在地球上,任何大圓,在任何方向上,都可以用來測量地球的周長。大圓是在球體周圍可能畫出的最大的圓。通過像地球這樣的球體上的任何兩點,無論分隔它們的線的方向如何,都可以定義并畫出一個大圓。通常繪制的大圓是地球的經線,都經過南北兩極。在一條緯度線上只有一個大圓:赤道。但是地球周圍有無數的大圓,它們的中心都在地球的中心(圖1.2)。
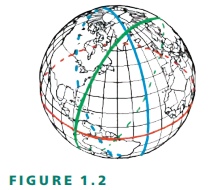
三個大圓,一個在赤道(紅色),一個沿著經度(藍色)和另一個隨機方向(綠色)。
在陽光下的垂直結構,如柱子和樹木,會投下陰影。因為到達地球表面的陽光是彼此平行的,附近垂直的樹木投射出等角度的陰影。但由于地球的曲率,在一天中的同一時間,許多公里外的樹木投下的陰影與陽光的角度不同。由于太陽在天空中連續移動,幾分鐘后,陰影的角度會略有不同。令人驚訝的是,樹木或其他垂直結構在地球不同地方投下的陰影,無論是在經線上還是在經線外,都為計算地球的大小提供了足夠的信息。
任何一對垂直結構在陽光下投射的陰影,間隔一定距離,為計算地球的周長提供了足夠的信息。
地球的大小可以用簡單的三角學來計算,當一棵樹的陰影直接指向或遠離第二棵樹時。在這個特殊的時刻,陽光照射地球的平面與這對樹所形成的大圓的平面是一致的。如圖1.3所示,地球中心的10°頂點等于太陽光與垂直樹木的角度差值10°。
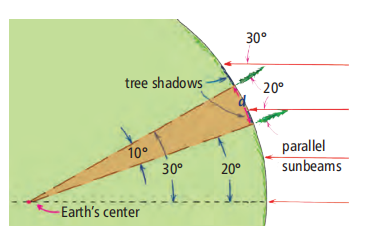
圖1.3
這兩棵樹的弧線在地球中心夾角為10°(用棕色的“楔”表示)。
有多少個10°的地球段構成了完整的360°地球周長?答案是360°/10°= 36。這告訴我們,地球的周長等于36乘以這兩棵樹之間的距離。任務完成!
旗桿更擅長投射清晰的陰影。對于相隔遙遠的城市,距離是已知的量,一個有趣的科學項目(或活動)是將成對樹的想法應用到你的學校和另一個城市的學校的旗桿上。
在地球上的任何地方,除了極少數例外,一對旗桿在陽光下的影子都會在某一天的某個時間排成一個大圓。為了計算地球的周長,你必須找到一個日期和時間,當你學校的旗桿投下的陰影直接指向或直接遠離另一個城市的學校旗桿。如果另一個城市有陽光,那里的影子也會同時滿足同樣的標準。如果是陰天或雨天,或者是周末,要有耐心:幾乎相同的情況會持續好幾天。(注意:測量不落在大圓平面上的入射光線涉及更復雜的球面三角學。)
埃拉托色尼的同步讀數是通過夏至時經線附近的陰影實現的。有了智能手機,他就可以沿著地球的任何一個大圓,甚至赤道,計算出地球在任何一天的大小。
你擁有了埃拉托色尼做夢也想不到的東西:互聯網和智能手機,也許還有一個指南針,可以判斷投射的陰影何時對齊(第一個指向第二個,第二個遠離第一個,或者在某些情況下,每個影子都指向另一個)。埃拉托色尼的同步計時問題是由智能手機提供的。兩個測量角度的差值(或者,如果陰影彼此遠離,則其和)等于每個旗桿的延伸垂直線在地球中心相交的頂點處的角度。請注意,在草圖中,當平行陽光的平面與雙旗桿大圓的平面重合時,兩旗上的太陽光角度之差等于地球中心的頂角。有了良好的數據,就可以計算出地球的周長。
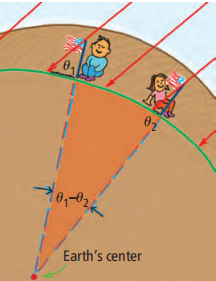
或者考慮反過來做:用地球4萬公里的周長作為已知值,找出相隔遙遠的旗桿之間的未知距離。旗桿必須離得很遠才能達到好的效果。例如,100公里的分離距離對應的太陽光角度差異小于1°,這很難區分。你們的地點相隔遠一點會更好。不管你是決定計算地球的周長,還是計算你們之間的距離,這都是一項引人入勝的合作活動。去吧!
我的想法:把這個變形一下,有:
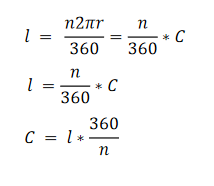
l ≈ 111.1111 * n。
角度??(a、c是投影長度,b、d是垂直結構長度)
最后推得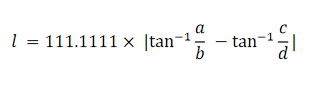
埃拉托色尼也會得到同樣的結果,因為他完全忽略了度數,并將柱子投下的影子的長度與柱子的高度進行比較。當埃拉托色尼測量陽光與垂直柱的7.2°夾角時,他還注意到柱子投下的陰影是柱子高度的1/8(圖1.4)。幾何推理近似地表明,陰影長度/柱子高度之比與亞歷山大和Syene之間的距離之比/地球半徑之比相同。所以,就像柱子比它的影子高8倍一樣,地球的半徑一定是亞歷山大和Syene之間距離的8倍。(相似三角形)
因為圓的周長是2π乘以它的半徑C = 2πr,地球的半徑就是它的周長除以2π。以現代單位計算,地球的半徑是6370公里,周長是40000公里。
所以我們知道埃拉托色尼測量地球大小的方法不止一種。在接下來的章節中,我們將會一次又一次地遇到這種通向解決方案的多條路徑的特性。這是優秀科學的標志,也是人們投身于物理學或物理相關專業的眾多原因之一。向物理學致敬。
1.1.5 月亮的大小
與埃拉托色尼同時代的另一位希臘科學家是阿里斯塔克斯,他可能是第一個提出地球每天繞地軸自轉一次的人,這就解釋了恒星每天的運動。阿里斯塔克斯還假設地球繞太陽公轉一年,其他行星也是如此。他正確地計算出了月球的直徑和它到地球的距離。他在公元前240年左右完成了這一切,比他的發現被完全接受還要早17個世紀。阿里斯塔克斯通過觀察月食來比較月球和地球的大小。地球,像陽光下的任何物體一樣,都會投下陰影。月食僅僅是月球進入這個陰影的事件。阿里斯塔克斯仔細研究了這一事件,發現地球陰影在月球上的寬度是月球直徑的2.5倍。這似乎表明月球的直徑比地球的直徑小2.5倍。前提是來自太陽相對邊緣的光線彼此完全平行。雖然太陽光線在短距離內幾乎是平行的,但由于太陽的巨大尺寸,它們的輕微變細在較長的距離上是明顯的,如在日食期間(圖1.5),當來自太陽上下邊緣的光線變細到幾乎一個點時。在月球到地球的距離上,光線變細了大約一個月球直徑。在月食期間,地球的影子在相同距離上也會出現相同的錐度(圖1.5右側)。如果考慮到太陽光線的逐漸變細,地球的直徑必須是月球直徑的2.5 + 1倍。通過這種方式,阿里斯塔克斯證明了月球的直徑是地球的1/3.5。目前公認的月球直徑為3640公里,與阿里斯塔克斯計算的值相差不到5%。
注:阿里斯塔克斯對他的日心說不確定,可能是因為地球不相等的季節似乎不支持地球繞太陽轉的觀點。更重要的是,人們注意到月球與地球的距離是不同的——這清楚地證明了月球并不是完美地繞著地球轉。如果月球不是繞著地球圓周運動,那么很難說地球繞著太陽圓周運動。行星橢圓軌道的解釋直到幾個世紀后才被約翰內斯·開普勒發現。與此同時,其他天文學家提出的本輪解釋了這些差異。如果月球不存在,推測天文學的進程是很有趣的。它的不規則軌道不會影響到早期對日心說的質疑,因為日心說可能在幾個世紀前就已經成立了。
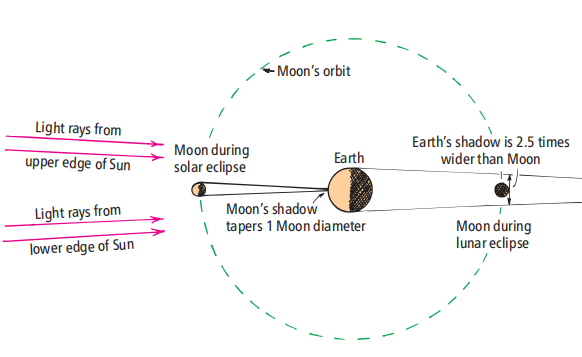
圖1.5
在月食期間,地球的陰影被觀測到是月球直徑的2.5倍。由于太陽的巨大體積,地球的陰影必須逐漸縮小。在日食期間,月球的陰影逐漸變細,從月球到地球的直徑相當于整個月球的直徑。因此,在月食期間,地球的影子在相同距離上變小的幅度相同。因此,地球的直徑一定是月球直徑的3.5倍。

日食和月食的正確比例,這說明了為什么太陽、月亮和地球的完美陣容不會每月出現。(月食更罕見,因為月球的軌道與地球圍繞太陽的軌道平面傾斜約5°。)
1.1.6 到月球的距離
把一枚小硬幣,比如一角硬幣,粘在窗戶上,用一只眼睛觀看,這樣它就能擋住滿月。當你的眼睛距離硬幣大約110個硬幣直徑時,就會發生這種情況。那么硬幣直徑/硬幣距離的比值約為1/110。相似三角形的幾何推理表明,這也是月球直徑/月球距離的比值(圖1.7)。所以你到月球的距離是月球直徑的110倍。早期的希臘人知道這一點。阿里斯塔克斯對月球直徑的測量是計算地月距離所需要的全部資料。因此,早期希臘人既知道月球的大小,也知道它到地球的距離。
有了這些信息,阿里斯塔克斯計算出了地球到太陽的距離。
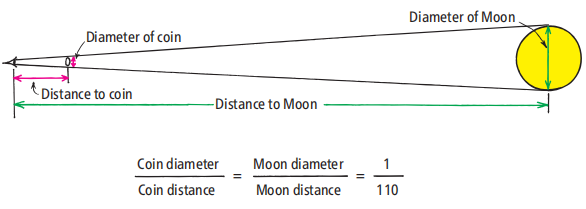
圖1.7
一個比例練習:當硬幣幾乎沒有“遮住”月球時,硬幣的直徑與你與硬幣之間的距離之比等于月球的直徑與你與月球之間的距離之比(這里沒有比例)。兩個比值的測量值均為1/110。
它這里怎么測月球直徑沒細講,我查了下資料,古希臘的阿里斯塔克斯等人是這么做的:
①?觀測月食:? 記錄月球完全進入地球本影(全食階段)到開始離開本影(偏食階段結束)所需的時間。
② 理解陰影錐:? 地球投射到太空的本影是一個錐形(像冰淇淋筒)。離地球越遠,本影的橫截面越小。
③?建立比例關系:
月球穿過地球本影的直徑所需的時間(T_pass)。
月球繞地球公轉一周(一個朔望月)所需的時間(T_month)。
T_pass / T_month 這個比例,理論上應該等于(地球本影在月球軌道處的直徑) / (月球公轉軌道的周長)。
④?引入地球直徑:通過測量不同緯度上同一顆恒星的地平高度差等方法,埃拉托斯特尼(Eratosthenes)等人已經相當準確地測量了地球的直徑(D_earth)。
⑤?結合地球直徑、太陽距離(阿里斯塔克斯曾嘗試估算,但誤差很大)、以及上述時間比例,利用相似三角形等幾何關系,可以推算出地球本影在月球軌道處的直徑(D_shadow)。然后,結合月食持續時間和月球軌道速度等,最終推算出月球直徑(D_moon)與地球直徑(D_earth)的比例關系。
結果:? 阿里斯塔克斯得出的結論是地球直徑大約是月球直徑的2.85倍(實際值接近3.67倍),誤差較大。但他的方法在原理上是正確的,為后世奠定了基礎。喜帕恰斯等人的測量更精確一些。
1.1.7 到太陽的距離
如果你要對太陽重復硬幣和月亮的練習(因為太陽的亮度,這樣做是危險的),猜猜會發生什么?太陽直徑與太陽距離的比值也是1/110。這是因為太陽和月亮的大小對眼睛來說是一樣的。它們都變細成相同的角度(約0.5°)。雖然早期希臘人已經知道直徑與距離的比值,但直徑或距離本身必須通過其他方法來確定。阿里斯塔克斯找到了一種方法。他是這樣做的。
阿里斯塔克斯觀察月相的時候,月亮正好是半圓的,太陽仍然在天空中可見。那么,照在月球上的陽光一定與他的視線成直角。這意味著地球和月球之間、地球和太陽之間以及月球和太陽之間的線形成了一個直角三角形(圖1.8)。
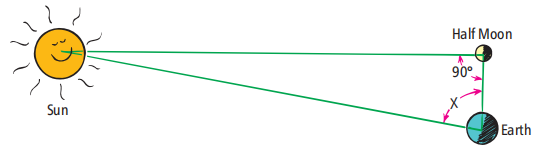
圖1.8
當月亮正好出現半圓時,太陽、月亮和地球形成一個直角三角形(不按比例)。斜邊是地球到太陽的距離。通過簡單的三角學,只要知道任意一個非直角的大小和其中一條邊的長度,就可以求出直角三角形的斜邊。地月距離是一個已知長度的邊。測量角度X,你就可以計算出地球與太陽的距離。三角學的一個規則是,如果你知道一個直角三角形的所有角加上它的任意一條邊的長度,你就可以計算出任何其他邊的長度。阿里斯塔克斯知道地球到月球的距離。在半月出現的時候,他還知道其中一個角度:90°。他所要做的就是測量月球視線和太陽視線之間的第二個角度。然后第三個角,一個很小的角,是180°減去前兩個角的和(任何三角形的內角和等于180°)。
如果沒有現代的凌日觀測,測量月球和太陽的視線之間的角度是很困難的。首先,太陽和月亮都不是點,而是相對較大的。阿里斯塔克斯必須觀察它們的中心(或邊緣)并測量它們之間的夾角——相當大,幾乎是一個直角!按照現代的標準,他的測量方法非常粗糙。他測量到的是87°,而真實值是89.8°。他認為太陽的距離大約是月球的20倍,而實際上太陽的距離大約是月球的400倍。所以,盡管他的方法很巧妙,但他的測量結果卻不盡如人意。也許是阿里斯塔克斯覺得很難相信太陽離我們這么遠,所以他在太陽離我們這么近的那一邊搞錯了。我們不知道。
今天我們知道太陽離地球的平均距離是1.5億公里。它在1月初離地球較近(1.46億公里),在7月初離地球較遠(1.52億公里)。
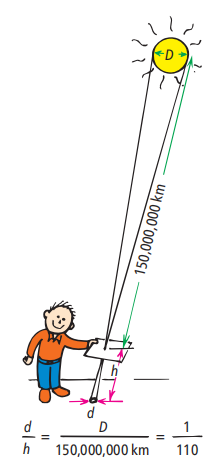
圖1.9
針孔投射出的圓形光斑是太陽的圖像。它的直徑/距離比與太陽直徑/日地距離比相同,為1/110。太陽的直徑是地球距離的1/110。
經典的小孔成像方法。
1.1.8 檢測點
1. 對月食的觀察如何使阿里斯塔克斯估算出月球的直徑?
阿里斯塔克斯目測到,在月食期間,地球在月球上的陰影比月球寬2.5倍。再加上太陽光線變細的影響,他估計地球的直徑一定是月球直徑的3.5倍。換句話說,月球的直徑是地球的1/3.5倍。所以月球的直徑是地球直徑的1/3.5倍,這是他同時代的埃拉托色尼測量的。
2. 阿里斯塔克斯是第一個以半個月亮為參照計算地球到太陽距離的人。為什么月球處于半月期很重要?
如圖1.8所示,地球到半月的距離、太陽到半月的距離、地球到太陽的距離組成了一個直角三角形。直角三角形很重要,因為如果你知道三角形任意邊的距離,你就可以計算出另外兩條邊的距離。根據他的測量(當時還不完善),阿里斯塔克斯計算出了地球到太陽的距離。
1.1.9 太陽的大小
一旦知道了太陽的距離,直徑/距離的1/110比率就可以測量太陽的直徑。除了圖1.7的方法外,另一種測量1/110比率的方法是測量通過針孔開口投射的太陽圖像的直徑。你應該試試這個。在一張不透明的硬紙板上戳一個洞,讓陽光照在上面。投射在下面的圓形圖像實際上是太陽的圖像。你會發現,圖像的大小并不取決于針孔的大小,而是取決于針孔離圖像的距離。黑洞越大圖像越亮,而不是越大。當然,如果洞很大,就不會形成圖像。孔的大小取決于它與所投射的圖像的距離。圖1.9中的孔可以是鋒利的鉛筆穿過紙板時產生的大小,直徑約為1毫米。圖1.10中Lillian上方樹葉間的“針孔”可以有幾厘米寬。無論如何,仔細的測量表明,圖像尺寸與“針孔”距離之比是1/110——與太陽直徑/太陽-地球距離之比相同(圖1.9)。
你有沒有注意到,當太陽在頭頂時,你在樹下的地面上看到的陽光斑點是完美的圓形,而當太陽在天空中低空時,你看到的陽光斑點呈橢圓形(圖1.10)?這些是太陽的針孔圖像,陽光通過樹葉上的開口照射,與地面的距離相比,樹葉上的開口很小。在距地面110 * 10厘米的開口處鑄造一個直徑10厘米的圓點。高大的樹木產生巨大的圖像;矮樹產生小圖像。
 .
.
樹葉之間的小洞在莉莉安周圍投射出太陽的圖像。
有趣的是,在日偏食時,針孔投射的圖像將是新月形的——與部分被覆蓋的太陽相同(圖1.11)。這提供了一種不用看太陽就能觀察日偏食的替代方法。

月牙形的陽光斑點是太陽部分日食時的圖像。
1.1.10 檢測點
1. 使用圖1.9所示的方法,我們得知太陽距離我們有110個太陽。在圖1.7中,我們知道月球距離我們有110個月球。這是巧合嗎?
是。太陽和月亮的角度相同,形成了1/110的比例,這完全是巧合。在過去,月球與地球的距離明顯更近,與地球的夾角也更大。目前,月球正在以每年大約4厘米的速度緩慢地遠離地球(由于潮汐摩擦和角動量守恒的影響)。這意味著在未來的幾年里,月球在天空中會顯得更小,產生日環食而不是日全食。
2. 如果圖1.9中卡片的高度被放置,使太陽圖像與硬幣的大小相匹配(測量太陽圖像直徑的精確方法),那么這些硬幣中的110個將首尾相連地放在卡片和下面圖像之間的空間中。地球和太陽之間同樣可以容納多少個太陽?
答案是,從太陽到地球之間的空間可以容納110個太陽。如果你做一個類似的實驗,在低滿月的時候把一枚硬幣粘在你的窗戶上,你會發現從窗戶到你的眼睛之間正好有110枚硬幣,這說明110個月亮可以填滿地球和月球之間的平均空間。
1.1.11?數學——科學的語言
大約四個世紀以前,科學和數學結合之后,科學和人類的狀況有了巨大的進步。當科學的思想用數學術語表達時,它們是明確的。科學方程式為概念之間的關系提供了簡潔的表達。它們沒有多重含義,而這些含義通常會讓用普通語言表達思想的討論感到困惑。當自然界的發現被數學表達出來時,它們更容易被實驗證實或推翻。物理學的數學結構將在你將在本書中遇到的許多方程中顯而易見。這些方程式是思維的指南,展示了自然界中概念之間的聯系。數學方法和實驗方法導致了科學上的巨大成功。
注意:我們區分物理的數學結構和數學解決問題的實踐——這是大多數非概念性課程的重點。請注意,與練習的數量相比,本書各章末尾的問題相對較少。重點在于計算前的舒適理解。附加的問題是在解決問題的概念物理輔助書。
第一章的第一節結束。
PS:在這里感嘆古希臘的科學家好厲害,真想學下它們的方法操作一下,體會下古人的智慧。
但是等到月食出現的時候再測量,太久了~。
DeepSeek教我一招,叫
手機攝影視差法
原理?
兩地同時拍攝月亮相對于恒星背景的位置差 → 三角視差計算距離
所需工具?
兩部智能手機(帶專業拍照模式)
三腳架(固定手機)
免費軟件:Stellarium(星圖)、Image??????(測量像素距離)
?操作步驟
組建觀測網?:
找異地同學(基線距離L≥500 km,如北京-上海)
約定?同一時刻?(精確到秒)拍攝月亮與亮星(如畢宿五)
拍攝要求?:
手動模式:ISO 100,曝光1/100s,焦距放大至最大
包含參考星(如月球旁3°內的亮星)
數據分析?:
用ImageJ測量兩地照片中?月心到參考星的像素距離?(例:Δp?=120px, Δp?=150px)
計算視差角:
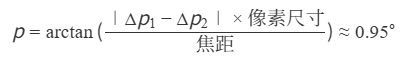
地月距離?:
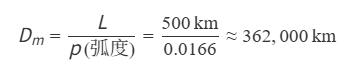
?精度提升技巧?
選擇月亮靠近亮星時(每月多次機會)
用多顆恒星平均定位(降低隨機誤差)
基線L用Google Earth精確測量(誤差<1%)
挺意思有趣,但我還是算了,還是看身邊有沒有對天文愛好的人做這個事情~

軟件調試---vscode配置clang-tidy靜態分析(30))

















