【數據結構】跳表的概率模型詳解與其 C 代碼實現

文章目錄

介紹
- 關鍵組成部分
- 讀者可以比對這張圖片去理解跳表 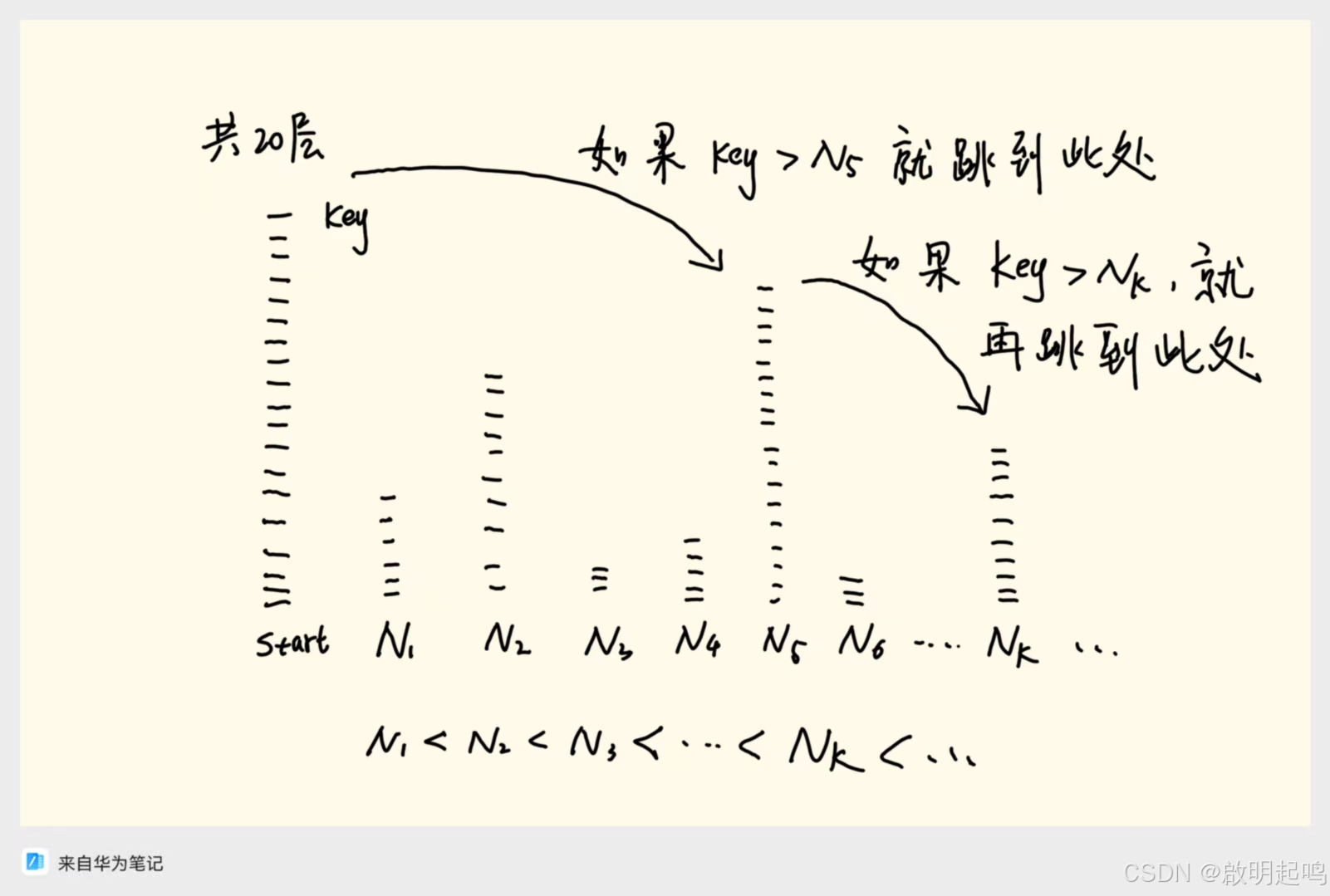![在這里插入圖片描述](https://i-blog.csdnimg.cn/direct/c5704b6276a14c3f9facdc3e55015bcc.jpeg#pic_center) 核心操作原理
- 算法的概率模型
跳表的 C代碼實現
- 初始化跳躍表的節點、跳躍表本身
- 跳表插入節點
- 查找元素
- 更新元素值
- 刪除跳表的某個節點
- 跳表的范圍查詢
- 銷毀跳躍表
- 按層級打印跳躍表
- 測試代碼（主函數）

推薦一個零聲教育學習教程，個人覺得老師講得不錯，分享給大家：[Linux，Nginx，ZeroMQ，MySQL，Redis，fastdfs，MongoDB，ZK，流媒體，CDN，P2P，K8S，Docker，TCP/IP，協程，DPDK等技術內容，點擊立即學習: https://github.com/0voice 鏈接。

介紹

跳表本質上是一種概率性的、有序的鏈表數據結構。它的核心目標是在有序鏈表的基礎上，通過添加多層索引來加速查找、插入和刪除操作，使得這些操作的平均時間復雜度能達到 O(log n)，媲美平衡二叉搜索樹（如AVL樹、紅黑樹），但通常實現起來更簡單，并且在某些并發場景下表現更好。

數據庫與存儲系統
LevelDB/RocksDB
應用：內存表（MemTable）實現
優勢：高效的范圍查詢支持（SSTable構建）；簡單的并發控制；自然的鍵排序
數據庫與存儲系統
Apache Cassandra
應用：內存中的有序數據結構
優勢：支持快速范圍掃描和點查詢
緩存系統
Redis有序集合（Sorted Set）
應用：有序集合的底層實現之一
優勢：
1、O(log N) 的ZADD、ZRANGE、ZREM操作
2、高效的范圍查詢（ZRANGEBYSCORE）
3、與哈希表結合提供O(1)的點查詢
搜索引擎與倒排索引
Lucene/Elasticsearch
應用：詞典存儲和區間查詢
優勢：快速術語查找；支持范圍查詢（如日期范圍）；高效的內存使用
網絡路由與協議
分布式哈希表（DHT）
應用：Chord協議等P2P網絡
優勢：高效的關鍵字查找（O(log N)跳）；自然支持區間查詢
實時數據處理
1、時間序列數據庫
應用：存儲時間戳數據點
優勢：高效的時間范圍查詢；按時間順序插入；支持滾動窗口統計
2、金融交易系統
應用：訂單簿管理
優勢：快速價格查詢；高效的范圍掃描（獲取買賣盤）

相比于各種樹（紅黑樹、B/B+樹、SPLAY 樹），跳表的好處是很多的。

場景	跳表優勢	平衡樹劣勢
并發環境	簡單的細粒度鎖或無鎖實現	復雜的全局重平衡
范圍查詢	底層鏈表自然支持順序訪問	需要復雜的中序遍歷
實現復雜度	代碼簡單，調試容易	旋轉操作復雜，易出錯
內存局部性	節點獨立，緩存友好	指針密集，緩存不友好
性能預測	平均O(log N)，實踐穩定	最壞情況保證但常數因子大

你可以把它想象成在一個有序的單鏈表（第0層）上，建立了一層或多層的“快速通道”（高層索引）。高層索引跨越更多的低層節點，讓你能更快地定位到目標區域。

跳表就像并排隨機生長的小草，我們查找數據就是類似于玩馬里奧游戲，從最左邊某處跳下，先跳到離自己最近的長得最高的那棵草上，然后平級跳躍，直至不能再跳才下降一層找其他地方跳。

在這里插入圖片描述
再仔細想一想，他真的很像一群并排生長的小草，小草的植高是隨機的。

關鍵組成部分

節點：
存儲實際的數據值（Key）。
包含一個forward指針數組（或叫next數組）。這個數組的大小等于該節點所在的層數（Level）。
forward[i] 指向該節點在第 i 層上的下一個節點。
層：
第0層：最底層，包含所有元素，是一個完整的有序鏈表。
第1層及以上：索引層。每一層都是其下一層的子集（一個更稀疏的有序鏈表）。層級越高，包含的節點越少，跨度越大。
頭節點：有一個特殊的頭節點（Head），它的層數等于跳表當前的最大層數（MaxLevel）。頭節點的 forward[i] 指向第 i 層的第一個實際節點（如果存在）。實際上是個一個哨兵節點。
最大層數：一個預先設定的或動態調整的限制，防止層數無限增長。通常用 MaxLevel 表示。
隨機層數：這是跳表“概率性”的核心。當插入一個新節點時，不是固定地把它加到所有層，而是用類似拋硬幣的方式（隨機算法）決定它應該出現在哪些層。常見方法是：
- 從第1層開始（第0層肯定包含）。
- 生成一個隨機數（比如0或1）。
  - 如果結果是“正面”（例如1），則將該節點添加到當前層，并嘗試向上一層（層數+1），重復拋硬幣。
  - 如果結果是“反面”（例如0），則停止增加層數。
- 確保節點至少在第0層（所以通常從第1層開始“拋硬幣”）。

最終節點的層數 lvl 是一個介于1和MaxLevel之間的隨機值（以1為起點）。這個節點將出現在第0層到第 lvl-1 層（或第1層到第 lvl 層，取決于定義）。

讀者可以比對這張圖片去理解跳表

核心操作原理

查找：
- 從最高層開始：從頭節點的最高層開始。
- 向右遍歷：沿著當前層的 forward 指針向右移動，直到下一個節點的值大于等于目標值。
- 向下一層：如果下一個節點的值大于目標值，或者當前層沒有下一個節點了，則下降到下一層。
- 重復：重復步驟2和3，直到下降到第0層。
- 檢查：在第0層，當前節點的下一個節點如果等于目標值，則找到；否則不存在。
插入：
- 查找插入位置：執行與查找類似的過程，但在下降過程中記錄每一層可能需要更新的前驅節點（即在新節點插入后，其 forward 指針需要指向新節點的那些節點）。這些節點存儲在 update 數組中，update[i] 保存第 i 層最后一個小于新節點值的節點。
生成隨機層數：使用拋硬幣法決定新節點的層數 lvl。
創建新節點：創建一個層數為 lvl 的新節點。
更新指針：（可選）更新最大層數：如果 lvl 大于當前跳表的最大層數，則更新頭節點的層數和跳表的 MaxLevel。
- 對于每一層 i (從0 到 lvl-1)：
  新節點的 forward[i] = update[i].forward[i]
  update[i].forward[i] = 新節點
刪除：
- 查找目標節點：執行與查找類似的過程，同樣記錄每一層可能需要更新的前驅節點（存儲在 update 數組中），這些節點的 forward 指針指向目標節點（或即將指向）。
- 找到目標節點：在第0層，update[0].forward[0] 應該就是目標節點（如果存在）。
更新指針：
對于每一層 i (從0 到目標節點層數-1)：
如果 update[i].forward[i] 等于目標節點，則 update[i].forward[i] = 目標節點.forward[i]
刪除節點：釋放目標節點內存。
（可選）降低最大層數：如果刪除的是最高層的唯一節點，可能需要降低頭節點的層數和跳表的 MaxLevel。

讀者可以繼續參考這張圖
在這里插入圖片描述

算法的概率模型

每個節點的層高有一套統計學操作程序決策，插入一個節點后，采用隨機數判斷是否提高層數。只要隨機數都指向要上升一級，那就層數加 1；但是只要某一次沒有指向層數上升的決定，那么決策終止，節點的層高就此敲定。

如果本科學過概率論，就會發現這就是經典的幾何分布。

幾何分布（Geometric Distribution）

定義：在一次伯努利試驗中，成功的概率為 p（0 < p ≤ 1），失敗的概率為 q = 1 – p。
獨立重復地進行該試驗，直到第一次成功為止，所進行的試驗總次數記為隨機變量 X。
則 X 服從參數為 p 的幾何分布，記作? $\sim Ge(p)$
分布律（概率質量函數，PMF）
對于 k = 1, 2, 3, … $P(X = k) = q^{k-1} p$
解釋：前 k – 1 次均失敗（概率 q^{k-1}），第 k 次首次成功（概率 p）。
期望（均值）
??E[X] = 1 / p
方差（誤差）
??Var(X) = q / p2 = (1 – p) / p2

期望與方差的計算都是使用無窮級數里的冪級數函數項級數的技巧方法，讀者可以參考《數學分析》。

對于我的 C 代碼實現，一般來說，每次決策都是有一半的概率提升層數，也有一半的概率不提升節點的層數，故而平均層數為兩層，
$E [X] = 1/ p = 2, 當 p = 0.25 時 .$

算法的查找復雜度（跳表總體層高依較大概率小于某個數）

我們記 $N_{max}$ 為節點總數為 $N$ 時的總體層高（它是一個隨機變量），記 K(N) 為隨機變量 $N_{max}$ 的某個概率上界。一個節點的層高大于 K(N) 的概率是 $1?12K(N)1-\frac{1}{2^{K(N)}}$ ，故而

$P(Nmax≤K(N))≤(1?12K(N))NP(N_{max} \leq K(N)) \leq (1-\frac{1}{2^{K(N)}})^N$

此時我們發現，如果 $K(N) =2*\log_2 N$
$P(Nmax≤K(N))≤(1?1N2)N=(1e)N→0,當N→∞.P(N_{max} \leq K(N)) \leq (1-\frac{1}{N^2})^N=(\frac{1}{e})^N\to 0,\; 當\;N\to \infty.$

所以我們可以算出跳躍表的層高是依概率小于 $2\log_2 N$ 的。

跳表的 C代碼實現

我們需要明確的一點是
$數據結構 = 數據定義 + 數據的操作方法。$
首先是數據定義，每個節點都帶有一個跳躍數組 forword，與鍵值對。跳表需要包括頭節點（頭節點是一個哨兵節點）、當前元素數量、當前層高。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <limits.h>//  跳表就像并排隨機生長的小草，我們查找數據就是類似于玩馬里奧游戲，從最左邊某處跳下，先跳到離自己最近的長得最高的那棵草上，然后平級跳躍，直至不能再跳才下降一層找其他地方跳
// 跳表最大層數，越大說明稀疏程度越高
#define MAX_LEVEL 16// 跳表節點結構
typedef struct Node {int key;int value;struct Node **forward;  // 每層的前進指針數組
} Node;// 跳表結構
typedef struct SkipList {Node *header;           // 頭節點int level;              // 當前最大層數int size;               // 元素數量
} SkipList;

初始化跳躍表的節點、跳躍表本身

// 創建新節點
Node* create_node(int level, int key, int value) {Node *node = (Node*)malloc(sizeof(Node));node->key = key;node->value = value;node->forward = (Node**)malloc(sizeof(Node*) * (level + 1));for (int i = 0; i <= level; i++) {node->forward[i] = NULL;}return node;
}// 初始化跳表
SkipList* create_skip_list() {SkipList *sl = (SkipList*)malloc(sizeof(SkipList));sl->level = 0;sl->size = 0;sl->header = create_node(MAX_LEVEL, INT_MIN, 0); // 頭節點鍵值為最小值，頭節點的層高一開始也是為 0// 初始化頭節點的每層指針for (int i = 0; i <= MAX_LEVEL; i++) {sl->header->forward[i] = NULL;}srand(time(NULL)); // 初始化隨機數種子return sl;
}

跳表插入節點

我們可以使用奇數與偶數的均勻二分，從而實現成功/失敗概率的 1：1。插入，首先進行的是跳躍查找定位到專門的節點。

// 隨機生成節點層數（偶數與奇數對半分）
int random_level() {int level = 0;while (rand() % 2 == 0 && level < MAX_LEVEL) {level++;}return level;
}// 插入元素
void insert(SkipList *sl, int key, int value) {Node *update[MAX_LEVEL + 1];    //  記錄條，記錄 key 的下確界Node *current = sl->header;// 從最高層開始查找插入位置for (int i = sl->level; i >= 0; i--) {while (current->forward[i] != NULL && current->forward[i]->key < key) {current = current->forward[i];}update[i] = current;}// 移動到第0層的下一個節點current = current->forward[0];// 如果鍵已存在，更新值if (current != NULL && current->key == key) {current->value = value;return;}// 隨機生成新節點層數int new_level = random_level();// 如果新節點層數大于當前跳表層數，更新高層指針if (new_level > sl->level) {for (int i = sl->level + 1; i <= new_level; i++) {update[i] = sl->header;}sl->level = new_level;}// 創建新節點Node *new_node = create_node(new_level, key, value);// 更新指針for (int i = 0; i <= new_level; i++) {new_node->forward[i] = update[i]->forward[i];update[i]->forward[i] = new_node;}sl->size++;
}

查找元素

// 查找元素
Node* search(SkipList *sl, int key) {Node *current = sl->header; //  current 是下確界// 從最高層開始查找for (int i = sl->level; i >= 0; i--) {while (current->forward[i] != NULL && current->forward[i]->key < key) {current = current->forward[i];}}// 移動到第0層的下一個節點current = current->forward[0];if (current != NULL && current->key == key) {return current;}return NULL;
}

更新元素值

// 更新元素值
void update(SkipList *sl, int key, int new_value) {Node *node = search(sl, key);if (node != NULL) {node->value = new_value;}
}

刪除跳表的某個節點

// 刪除元素
void delete(SkipList *sl, int key) {Node *update[MAX_LEVEL + 1];    // update 是下確界Node *current = sl->header;// 從最高層開始查找for (int i = sl->level; i >= 0; i--) {while (current->forward[i] != NULL && current->forward[i]->key < key) {current = current->forward[i];}update[i] = current;}// 移動到第0層的下一個節點current = current->forward[0];// 如果節點存在則刪除if (current != NULL && current->key == key) {// 更新各層指針for (int i = 0; i <= sl->level; i++) {if (update[i]->forward[i] != current) break;update[i]->forward[i] = current->forward[i];}// 釋放節點內存free(current->forward);free(current);// 更新跳表層數while (sl->level > 0 && sl->header->forward[sl->level] == NULL) {sl->level--;}sl->size--;}
}

跳表的范圍查詢

我們可以類比的是 B+ 樹的范圍查詢，因為它和 B+ 樹的范圍查詢一樣好用。讀者可以參考我寫的關于 B+ 樹的博客。

// 范圍查詢（高效實現）
void range_query(SkipList *sl, int start_key, int end_key) {Node *current = sl->header;// 定位到起始位置for (int i = sl->level; i >= 0; i--) {while (current->forward[i] != NULL && current->forward[i]->key < start_key) {current = current->forward[i];}}// 移動到起始節點current = current->forward[0];// 遍歷范圍內的節點printf("Range query [%d, %d]:\n", start_key, end_key);while (current != NULL && current->key <= end_key) {printf("  (%d, %d)\n", current->key, current->value);current = current->forward[0];}
}

銷毀跳躍表

// 銷毀跳表
void free_skip_list(SkipList *sl) {Node *current = sl->header;Node *next;// 釋放所有節點，跳表往右收縮，先刪頭節點while (current != NULL) {next = current->forward[0];free(current->forward);free(current);current = next;}//free(sl->header);free(sl);printf("all component have been release\n");
}

按層級打印跳躍表

// 打印跳表結構（調試用）
void print_skip_list(SkipList *sl) {printf("Skip List (level=%d, size=%d):\n", sl->level, sl->size);for (int i = sl->level; i >= 0; i--) {Node *node = sl->header->forward[i];printf("Level %d: ", i);while (node != NULL) {printf("%d(%d) → ", node->key, node->value);node = node->forward[i];}printf("NULL\n");}
}

測試代碼（主函數）

test_num 是指代測試規模。我們先插入一堆節點，然后按層級打印，緊接著是更改、查詢操作，最后是范圍查詢、刪除一個節點后再展示層級打印。


#define test_num 100
int main() {SkipList *sl = create_skip_list();for (int i=0; i<test_num; i++) {insert(sl, i+3, 3*i+17);}// 打印跳表結構print_skip_list(sl);// 查找示例Node *found = search(sl, 5);if (found) {printf("\nFound key 5, value=%d\n", found->value);}// 更新示例update(sl, 5, 555);printf("After update key 5: ");found = search(sl, 5);if (found) printf("value=%d\n", found->value);// 范圍查詢示例range_query(sl, test_num, 3*test_num);// 刪除示例delete(sl, 5);printf("\nAfter deleting key 5:\n");print_skip_list(sl);// 銷毀跳表free_skip_list(sl);return 0;
}

代碼運行

qiming@qiming:~/share/CTASK/data-structure$ gcc -o skiplist skiplist.c
qiming@qiming:~/share/CTASK/data-structure$ ./skiplist 
Skip List (level=7, size=100):
Level 7: 77(239) → NULL
Level 6: 77(239) → NULL
Level 5: 57(179) → 77(239) → NULL
Level 4: 30(98) → 57(179) → 68(212) → 77(239) → 88(272) → NULL
Level 3: 16(56) → 30(98) → 39(125) → 57(179) → 58(182) → 62(194) → 66(206) → 68(212) → 77(239) → 80(248) → 88(272) → 97(299) → NULL
Level 2: 5(23) → 14(50) → 16(56) → 18(62) → 30(98) → 39(125) → 57(179) → 58(182) → 62(194) → 66(206) → 68(212) → 77(239) → 80(248) → 88(272) → 90(278) → 94(290) → 96(296) → 97(299) → NULL
Level 1: 5(23) → 7(29) → 11(41) → 12(44) → 14(50) → 16(56) → 17(59) → 18(62) → 22(74) → 25(83) → 26(86) → 27(89) → 30(98) → 31(101) → 33(107) → 39(125) → 40(128) → 44(140) → 45(143) → 48(152) → 49(155) → 54(170) → 55(173) → 56(176) → 57(179) → 58(182) → 62(194) → 63(197) → 66(206) → 68(212) → 70(218) → 74(230) → 77(239) → 80(248) → 88(272) → 90(278) → 92(284) → 93(287) → 94(290) → 96(296) → 97(299) → NULL
Level 0: 3(17) → 4(20) → 5(23) → 6(26) → 7(29) → 8(32) → 9(35) → 10(38) → 11(41) → 12(44) → 13(47) → 14(50) → 15(53) → 16(56) → 17(59) → 18(62) → 19(65) → 20(68) → 21(71) → 22(74) → 23(77) → 24(80) → 25(83) → 26(86) → 27(89) → 28(92) → 29(95) → 30(98) → 31(101) → 32(104) → 33(107) → 34(110) → 35(113) → 36(116) → 37(119) → 38(122) → 39(125) → 40(128) → 41(131) → 42(134) → 43(137) → 44(140) → 45(143) → 46(146) → 47(149) → 48(152) → 49(155) → 50(158) → 51(161) → 52(164) → 53(167) → 54(170) → 55(173) → 56(176) → 57(179) → 58(182) → 59(185) → 60(188) → 61(191) → 62(194) → 63(197) → 64(200) → 65(203) → 66(206) → 67(209) → 68(212) → 69(215) → 70(218) → 71(221) → 72(224) → 73(227) → 74(230) → 75(233) → 76(236) → 77(239) → 78(242) → 79(245) → 80(248) → 81(251) → 82(254) → 83(257) → 84(260) → 85(263) → 86(266) → 87(269) → 88(272) → 89(275) → 90(278) → 91(281) → 92(284) → 93(287) → 94(290) → 95(293) → 96(296) → 97(299) → 98(302) → 99(305) → 100(308) → 101(311) → 102(314) → NULLFound key 5, value=23
After update key 5: value=555
Range query [100, 300]:(100, 308)(101, 311)(102, 314)After deleting key 5:
Skip List (level=7, size=99):
Level 7: 77(239) → NULL
Level 6: 77(239) → NULL
Level 5: 57(179) → 77(239) → NULL
Level 4: 30(98) → 57(179) → 68(212) → 77(239) → 88(272) → NULL
Level 3: 16(56) → 30(98) → 39(125) → 57(179) → 58(182) → 62(194) → 66(206) → 68(212) → 77(239) → 80(248) → 88(272) → 97(299) → NULL
Level 2: 14(50) → 16(56) → 18(62) → 30(98) → 39(125) → 57(179) → 58(182) → 62(194) → 66(206) → 68(212) → 77(239) → 80(248) → 88(272) → 90(278) → 94(290) → 96(296) → 97(299) → NULL
Level 1: 7(29) → 11(41) → 12(44) → 14(50) → 16(56) → 17(59) → 18(62) → 22(74) → 25(83) → 26(86) → 27(89) → 30(98) → 31(101) → 33(107) → 39(125) → 40(128) → 44(140) → 45(143) → 48(152) → 49(155) → 54(170) → 55(173) → 56(176) → 57(179) → 58(182) → 62(194) → 63(197) → 66(206) → 68(212) → 70(218) → 74(230) → 77(239) → 80(248) → 88(272) → 90(278) → 92(284) → 93(287) → 94(290) → 96(296) → 97(299) → NULL
Level 0: 3(17) → 4(20) → 6(26) → 7(29) → 8(32) → 9(35) → 10(38) → 11(41) → 12(44) → 13(47) → 14(50) → 15(53) → 16(56) → 17(59) → 18(62) → 19(65) → 20(68) → 21(71) → 22(74) → 23(77) → 24(80) → 25(83) → 26(86) → 27(89) → 28(92) → 29(95) → 30(98) → 31(101) → 32(104) → 33(107) → 34(110) → 35(113) → 36(116) → 37(119) → 38(122) → 39(125) → 40(128) → 41(131) → 42(134) → 43(137) → 44(140) → 45(143) → 46(146) → 47(149) → 48(152) → 49(155) → 50(158) → 51(161) → 52(164) → 53(167) → 54(170) → 55(173) → 56(176) → 57(179) → 58(182) → 59(185) → 60(188) → 61(191) → 62(194) → 63(197) → 64(200) → 65(203) → 66(206) → 67(209) → 68(212) → 69(215) → 70(218) → 71(221) → 72(224) → 73(227) → 74(230) → 75(233) → 76(236) → 77(239) → 78(242) → 79(245) → 80(248) → 81(251) → 82(254) → 83(257) → 84(260) → 85(263) → 86(266) → 87(269) → 88(272) → 89(275) → 90(278) → 91(281) → 92(284) → 93(287) → 94(290) → 95(293) → 96(296) → 97(299) → 98(302) → 99(305) → 100(308) → 101(311) → 102(314) → NULL
all component have been release
qiming@qiming:~/share/CTASK/data-structure$