全文 part1 - DGEMM Using Tensor Cores, and Its Accurate and Reproducible Versions

摘要

? ? ? ? 本文提出了一種在 NVIDIA 圖形處理器（GPU）的張量核心（Tensor Cores，僅含 FP16、INT8 等 GEMM 計算功能）上實現 FP64（雙精度，DGEMM）和 FP32（單精度，SGEMM）稠密矩陣乘法的方法。Tensor Cores?是一種特殊的處理單元，可對 FP16 輸入執行內聯圖形矩陣乘法并以 FP32 精度運算，最終返回 FP32 精度的結果。該方法采用 Ozaki 方案 —— 一種基于無誤差變換的精確矩陣乘法算法。所提方法具有三大顯著優勢：其一，可基于 cuBLAS 庫的 cublasGemmEx 例程，借助?Tensor Cores?操作構建；其二，能實現比標準 DGEMM 更高的精度，包括正確舍入結果；其三，即便核心與線程數量不同，也能確保位級可復現性。

? ? ? ? 該方法的可達性能取決于輸入矩陣各元素的絕對值范圍。例如，當矩陣以動態范圍為 1E+9 的隨機數初始化時，在 Titan RTX GPU（Tensor Cores?算力為 130 TFlops）上，我們實現的等效 DGEMM 操作可達約 980 GFlops 的 FP64 運算性能，而 cuBLAS 庫的 cublasDgemm 在 FP64 浮點單元上僅能達到 539 GFlops。研究結果表明，可利用 FP32/FP64 資源有限但低精度處理單元（如面向 AI 的處理器）運算速度快的硬件，來處理通用工作負載。

關鍵詞：Tensor Cores?；FP16；半精度；低精度；矩陣乘法；GEMM；線性代數；精度；可復現性

1. 引言

? ? ? ? 近年來，深度學習應用的日益增多推動了特殊處理單元的發展，例如 NVIDIA GPU 上的 Tensor Cores?以及谷歌的張量處理單元（TPUs）。此類任務的核心是矩陣乘法，其并不需要 IEEE 754-2008 binary32（即單精度，FP32，含 8 位指數和 23 位尾數）和 binary64（即雙精度，FP64，含 11 位指數和 52 位尾數）這樣的高精度。相應地，硬件更支持快速的低精度運算，如 binary16（即半精度，FP16，含 5 位指數和 10 位尾數）以及 INT8/INT16 位整數運算。

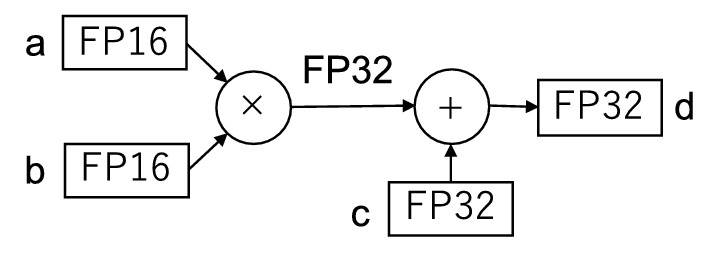
? ? ? ? 一個廣為熟知的例子是 Volta 架構中引入的 Tensor Cores?，其每時鐘周期可通過融合乘加操作完成一次 4x4 矩陣乘法。盡管 Tensor Cores??支持多種數據格式和計算精度，但本文聚焦于 FP32 精度模式下的 FP16 計算 —— 該模式以 FP32 精度執行 $d=a \times b +c$ ?運算（圖 1）。其中， $a$ ? 和 $b$ ? 為 FP16 值， $c$ ?和 $d$ ?為 FP32 值。Tensor Cores?的運算速度最高可達 CUDA 核心上標準 FP32 浮點單元（FPUs）的 8 倍。已有諸多研究在通用任務中充分利用了 Tensor Cores??的這一卓越性能。

? ? ? ?本文提出一種在 Tensor Cores?上計算 Level-3 基本線性代數子程序（BLAS）中通用矩陣乘法例程（GEMM）的方法，可支持 FP64（DGEMM）和 FP32（SGEMM）精度。GEMM 是眾多科學計算工作負載以及高性能 Linpack 測試中的核心操作之一。該方法基于 Ozaki 等人提出的一種基于無誤差變換的精確矩陣乘法算法（亦稱 Ozaki 方案）[13]。該方法的優勢如下：

高效實用：基于 NVIDIA 提供的 cuBLAS 庫中的 cublasGemmEx 例程構建，開發成本低；
精度更高：即便采用正確舍入，也能實現比標準 SGEMM 和 DGEMM 更高的精度；
可復現性強：對于相同輸入，即便每次執行時核心與線程數量不同，也能得到相同（位級一致）的結果；
適應性好：其理念可適配其他精度場景。

? ? ? ?部分研究通過利用低精度硬件來加速無需高精度的計算，而本文則嘗試借助低精度硬件實現更高精度的計算。我們的 DGEMM 實現僅在 FP64 支持有限的處理器上性能優于 cuBLAS 的 DGEMM。但相比之下，比 FP64 浮點單元的性能提升并非關鍵，更重要的是旨在提升低精度硬件（如面向人工智能的處理器）的潛力。此外，該方法為兼顧 AI 與傳統高性能計算（HPC）工作負載的高效硬件設計提供了新視角。例如，可減少 FP64 資源數量，轉而提供大規模低精度支持。

? ? ? ?本文其余部分結構如下：第 2 節介紹相關工作；第 3 節闡述基于 Ozaki 方案的方法；第 4 節介紹該方法的實現；第 5 節在 Titan RTX 和 Tesla V100 GPU 上進行精度與性能評估；第 6 節探討基于該方法的未來硬件設計方向；第 7 節總結全文。

2. 相關工作

? ? ? ?已有多項研究嘗試將為 AI 工作負載設計的低精度硬件用于其他場景。例如，Haidar 等人 [7] 在稠密與稀疏線性系統中，結合迭代精化技術利用了標準 FP16 和 FP32 精度模式下的張量核心操作。還有研究針對能效提升展開探討 [6]，Carson 與 Higham 則對此進行了誤差分析 [1]。Yang 等人 [16] 在谷歌 TPUs 上采用 bfloat16（BF16，含 8 位指數和 7 位尾數）實現了伊辛模型的蒙特卡洛模擬。這些研究將低精度運算應用于代碼中無需高精度的部分 —— 此類部分可在該精度水平下完成計算，因此其適用性取決于具體算法或問題。

? ? ? ?與本文類似，部分研究嘗試借助低精度硬件實現比硬件原生精度更高的運算。例如，Markidis 等人 [11] 提出了一種提升張量核心矩陣乘法計算精度的方法。盡管其方法在概念上與本文相似，但僅能對 FP16 支持的動態范圍內的矩陣進行計算，且精度與 SGEMM 相當。Henry 等人 [8] 探討了在 BF16 浮點單元上采用雙雙精度算術 [2]（一種經典的二重精度算術技術）執行高精度運算的性能。Sorna 等人 [15] 提出了一種提升張量核心上二維快速傅里葉變換精度的方法。需注意的是，這些研究中，獲得超過 FP32 或 FP64 浮點單元的性能并非關鍵，重點同樣在于提升低精度硬件的潛力。因此，可能需要重新設計硬件，以平衡浮點單元所支持的精度。本文的探討方向與之相近。

? ? ? ?本文所提方法的核心 ——Ozaki 方案，最初是為通過標準浮點運算實現精確矩陣乘法而提出的。OzBLAS [12] 基于 Ozaki 方案在 CPU 和 GPU 上實現了精確且可復現的 BLAS 例程。OzBLAS 基于 FP64 浮點單元上的 DGEMM 構建【注，結果的精度高于原始的 FP64 gemm】，而本文中的 Ozaki 方案則借助 Tensor Cores?上的 GEMM 執行 DGEMM/SGEMM 操作。Ichimura 等人 [10] 還報道了在多核 CPU 上基于 FP64 運算的 Ozaki 方案高性能實現。

3. 方法

? ? ? ?本節首先介紹通過改進的 Ozaki 方案在 Tensor Cores?上計算 DGEMM 的基本方案，隨后介紹用于提升計算速度的附加技術。本文中， $\text{fl}_\text{FP64}(\cdots)$ ? 和 $\text{fl}_\text{FP32}(\cdots)$ ?分別表示 FP64 和 FP32 算術下的計算； $\mathbf{u}_\text{FP64}$ ?和 $\mathbf{u}_\text{FP32}$ ?分別表示 FP64（ $\mathbf{u}_\text{FP64}=2^{-53}$ ）和 FP32（ $\mathbf{u}_\text{FP32}=2^{-24}$ ?）的單位舍入誤差【注, 單位舍入誤差解釋】； $\mathbb{F}_\text{FP64}$ ?和 $\mathbb{F}_\text{FP16}$ ?分別表示 FP64 和 FP16 浮點數的集合； $\mathbb{N}$ ?表示包含零的自然數集合。

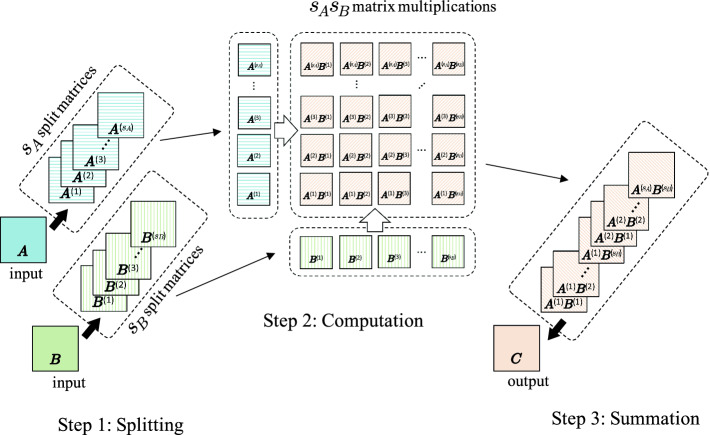
Fig. 2.?Schematic of matrix multiplication ( $C=AB$ ) by Ozaki scheme (in this figure, scaling is omitted).

3.1 適用于張量核心的 Ozaki 方案

? ? ? ?Ozaki 方案對矩陣乘法進行無誤差變換，具體而言，將矩陣乘法轉化為多個矩陣乘法的求和 —— 這些矩陣乘法可通過浮點運算執行且無舍入誤差。圖 2 為整個 Ozaki 方案的示意圖，該方法包含三個主要步驟：

拆分：對輸入矩陣按元素拆分得到多個子矩陣；
計算：計算所有子矩陣間的兩兩矩陣乘積；
求和：對上述所有子矩陣間的兩兩矩陣乘積?按元素求和。

? ? ? ? 下面詳細描述各步驟。為簡潔起見，我們以兩個向量 $x,y \in {\mathbb{F}_{\text{FP64}}}^n$ ?的內積為例進行說明，但該方法可自然擴展到矩陣乘法（矩陣乘法本質上由多個內積構成）。此外，盡管此處僅描述 DGEMM 的情況，但其理念同樣適用于 SGEMM。

步驟 1：拆分。算法 1 將 FP64 輸入向量拆分為多個 FP16 向量，過程如下：

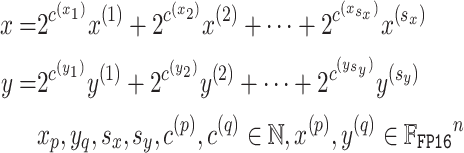
? ? ? ? 首先得到 FP64 格式的子向量，再將其轉換（降尺度）為 FP16 格式。該轉換僅調整指數，不會導致有效數字的 bit 丟失。其中， $2^{c^{(p)}}$ ?和 $2^{c^{(q)}}$ ?分別為向量 $x^{(p)}$ ?和 $y^{(q)}$ ?的指數從 FP64 到 FP16 的縮小因子。在算法 1 的第 7 行中，當 $\mu =\text{DBL\_MAX}$ ?時， $\tau$ ?達到 1024，這意味著 $c^{(p)}$ ?和? $c^{(q)}$ 可存儲為 2 字節 short 類型的整數。拆分算法需滿足以下特性：

1. 若 ${x^{(p)}}_i$ ?和? ${y^{(q)}}_j$ 為非零元素，則?

2.? $(x^{(p)})^Ty^{(q)}$ ? 在 FP32 計算中必須無誤差：

? ? ? ?拆分可理解為從浮點表示到定點表示的轉換。上述第一個特性意味著，通過省略最低階的部分子向量，可控制最終結果的精度（降低精度）。在一定數量的子向量下可獲得的最終結果精度，取決于內積的長度以及輸入向量各元素的絕對值范圍。需注意的是，若要將 Tensor Cores?替換為其他精度的浮點單元，需修改算法 1 中的參數 $\rho$ ，且被分割的向量（ $x^{(p)}$ ?和 $y^{(q)}$ ?）的 bit?數取決于浮點單元的精度。

步驟 2：計算。接下來，內積 $x^Ty$ ?按如下方式計算：

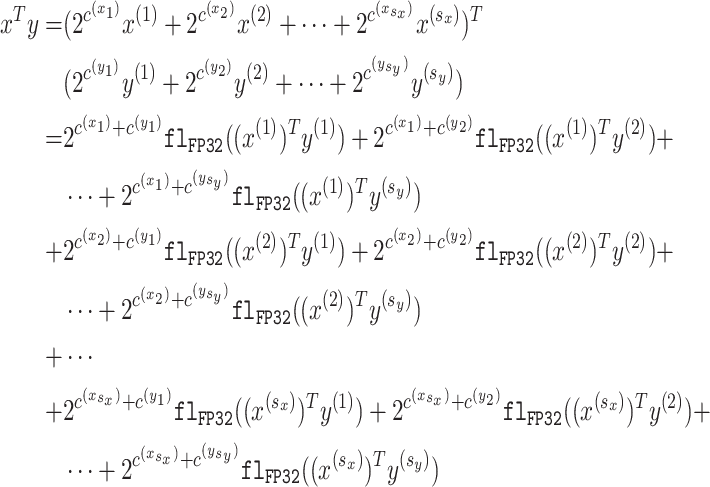
? ? ? ?此處需計算子向量間所有兩兩內積，共需計算 $s_xs_y$ ?個內積。 $2^{c^{(x_p)}+c^{(y_q)}}$ ? 為放大因子，用于補償拆分過程中的縮小操作。根據算法 1 的第二個特性，由于輸入為 FP16 格式，子向量的內積可通過?Tensor Core?操作計算。將該示例擴展到矩陣乘法時，必須基于標準內積算法對子矩陣進行乘法 —— 不允許采用 Strassen 算法等分治方法。

步驟 3：求和。最后，對子向量的內積進行求和。若所需精度為標準 DGEMM 的精度，求和可通過 FP64 算術完成。但由于步驟 2 中的 $\text{fl}_\text{FP32}((x^{(p)})^Ty^{(q)})$ ?無舍入誤差（無誤差），通過例如?NearSum [14] 等正確舍入方法進行求和，可得到 $x^Ty$ ?的正確舍入結果。即便在 FP64 算術中，若采用可復現的求和方法，結果也具有可復現性。由于求和是按元素進行的，計算順序易于固定。

矩陣乘法的完整流程。算法 2 在 Tensor Cores?上實現了矩陣乘法的完整 Ozaki 方案。其中，SplitA 和 SplitB 分別沿矩陣 $A$ ?和 $B$ ?的內積方向（k 維），采用算法 1 進行拆分。需注意的是，由于 $A_\text{split}$ ?和 $B_\text{split}$ ?可存儲為 FP16 格式， $\text{GEMM}_\text{FP32}$ ?可通過 cuBLAS 庫的 cublasGemmEx 例程，在 Tensor Core 上以 FP32 精度執行 FP16 計算。

3.2 快速計算技術

? ? ? ?為進一步提升性能，可通過以下方法修改算法 1 或算法?2。第 4 節將討論不改變算法的基于實現的加速技術。

快速模式。與 OzBLAS 的實現類似，我們定義參數 $d\in \mathbb{N},d\le \max{(s_x,s_y)}$ ?來確定計算中子矩陣的數量。指定后，可通過省略 $(x^{(p)})^Ty^{(q)}$ 中? $p+q>d+1$ ?的計算來減少計算量，但會導致精度略有損失。若所需精度為 FP64（與標準 DGEMM 相當，通過下述確定子矩陣數量的方法實現），則精度損失可忽略不計。該技術最多可將矩陣乘法的數量從 $d^2$ ?減少到 $d(d+1)/2$ 。

估算實現 FP64 等效精度所需的子矩陣數量。算法 1 在 $\mu=0$ ?時會自動停止拆分，即此時最終結果的精度達到最大。但如果所需精度為 FP64 算術下標準 DGEMM 的精度（FP64 等效精度），可基于概率誤差界 [9] 通過算法 3 估算所需的最小拆分次數：

其中， $e=(1,\cdots,1)^T$ ?的引入是為了避免在估算中進行矩陣乘法（需注意，在算法 3 的第 7 行中 $2^{c_A[d]_i} A_{\text{split}} [d]_{ij}$ ，為第 d 個未縮小的 FP64 子矩陣。因此，第 2 行的 SplitA到 $s_A$ ? 無需執行到，且可將 SplitA 與該算法集成）。該算法設計用于快速模式。若拆分次數按算法 1 執行到的方式確定，精度可能低于標準 DGEMM。此時，必須禁用快速模式。需注意的是，由于子矩陣數量僅基于概率誤差界估算，且會受向量 $e$ ?影響，該方法中期望精度（標準 DGEMM 所達精度）與實際獲得精度之間可能存在一定差異。

內積分塊。本研究暫未實現此步驟。由于算法 1 中的 $\rho$ ?包含內積維度 $n$ ，實現一定精度所需的拆分次數取決于矩陣的內積維度。通過對內積操作采用分塊策略，可避免拆分次數的增加。分塊大小可設置為實現最佳性能的最小尺寸。但該策略會增加求和成本，且除非執行正確舍入計算，否則改變分塊大小可能會影響可復現性。