二進制作為計算機底層數據的核心表示方式，其獨特的位結構和運算規則在算法設計中有著廣泛且關鍵的應用。以下從基礎操作、算法技巧、數據結構、經典問題等多個維度，全面梳理二進制在算法中的應用：

?
一、基礎位運算：算法的“原子操作”

?
二進制的核心優勢在于位運算的高效性（時間復雜度通常為O(1)），常見位運算包括：
?
與（&）：兩個位都為1則為1，否則為0。常用于“保留指定位”（如?x & mask?保留mask中1對應的位）。
?
或（|）：兩個位有一個為1則為1，常用于“設置指定位為1”（如?x | mask?將mask中1對應的位設為1）。
?
異或（^）：兩個位不同則為1，相同則為0。特性：?x ^ x = 0?，?x ^ 0 = x?，可用于“交換變量”“找唯一出現奇數次的數”等。
?
左移（<<）：?x << k??等價于 ?x * 2^k?（無溢出時），快速放大。
?
右移（>>）：?x >> k??等價于 ?x /2^k?（整數除法），快速縮小。
?
取反（~）：位反轉（0變1，1變0），常用于構造掩碼（如?~0?是全1的二進制）。
?
這些操作是二進制應用的基礎，幾乎所有二進制相關算法都依賴它們。

?
二、狀態壓縮：用二進制表示“集合狀態”

?
當問題需要表示“元素是否被選擇”“狀態是否激活”等集合信息時，二進制可將集合狀態壓縮為一個整數，大幅節省空間并簡化操作。
?
典型場景：
?
1.?子集枚舉
若有?n?個元素，每個子集可表示為一個?n?位二進制數（第?i?位為1表示元素?i?在子集中）。例如，?n=3?時，二進制?101?表示子集?{0, 2}?。
枚舉所有子集的代碼可簡化為：
python
? ?

for mask in range(0, 1 << n): ?# 1<<n 即2^n，覆蓋所有子集
? ? # mask的二進制表示即為一個子集
?
?
2.?動態規劃中的狀態壓縮
例如旅行商問題（TSP）：用?dp[mask][u]?表示“已訪問的城市集合為?mask?（二進制），當前在城市?u?時的最小距離”。其中?mask?的第?i?位為1表示城市?i?已訪問。
狀態轉移依賴位運算：?if not (mask & (1 << v))?（判斷城市?v?是否未訪問）。
?
3.?位掩碼優化
例如“N皇后問題”中，用三個整數（列、主對角線、副對角線）的二進制表示當前禁止放置的位置，通過位運算快速判斷合法性。

?
三、二進制特性：解決數學與計數問題

?
二進制的表示本身蘊含特殊規律，可用于優化數學問題的求解：
?
1.?判斷2的冪
若?n?是2的冪（如2、4、8），則二進制表示為?100...0?，滿足 ?n & (n-1) == 0?（如?8(1000) & 7(0111) = 0?）。
?
2.?計算二進制中1的個數（位計數）
方法1：循環檢查每一位（?count += n & 1; n >>= 1?）。
方法2：Brian Kernighan算法（高效）：?while n: n &= n-1; count +=1?（每次清除最后一個1）。
應用：漢明距離（兩數二進制不同位的數量，即?bin(x^y).count('1')?）。
?
3.?二進制分解（拆分為2的冪之和）
任何整數?n?都可分解為?n = 2^a + 2^b + ...?（如?5=4+1=2^2+2^0?）。
應用：貪心算法中，用最少的2的冪之和表示?n?（直接取二進制中1的位置）。
?
4.?高低位分離與合并
例如將32位整數的高16位和低16位分離：?high = (x >> 16) & 0xffff; low = x & 0xffff?，常用于哈希、加密等場景。

?
四、數據結構：基于二進制的高效設計

?
部分經典數據結構利用二進制的“分解性”（將問題拆分為2的冪次規模）實現高效操作：
?
1.?二進制索引樹（Fenwick Tree，樹狀數組）
核心思想：將數組索引分解為二進制表示（如?index=5(101)?可分解為?4+1=2^2+2^0?），通過樹狀結構存儲前綴和，支持O(log n)的單點更新和前綴和查詢。
應用：區間和、逆序對計數等。
?
2.?線段樹的二進制優化
線段樹的區間劃分基于“二分”，本質是二進制分解（將區間拆分為2的冪次長度的子區間），其查詢和更新效率（O(log n)）依賴于二進制的快速拆分。
?
3.?二進制堆
堆的結構是完全二叉樹，其父子節點索引關系（左子節點?2*i+1?，右子節點?2*i+2?）本質是二進制的左移操作（?i << 1?等價于?2*i?），因此堆的插入、刪除操作可通過位運算快速定位節點。

?
五、算法優化：用位運算替代傳統操作

?
二進制運算的高效性（硬件級支持）可優化算法的時間復雜度：
?
1.?替代算術運算
?
- 乘以/除以2的冪：?x * 8 = x << 3?，?x // 16 = x >> 4?（比乘法/除法快得多）。
?
- 判斷奇偶：?x & 1 == 1?（奇數），比?x % 2?更高效。
?
- 取模2的冪：?x % 8 = x & 7?（因為?8=2^3?，掩碼?7=111?）。
?
2.?變量交換（無需臨時變量）
利用異或特性：?a ^= b; b ^= a; a ^= b?（原理：?a ^ b ^ a = b?）。
?
3.?區間狀態快速更新
例如用二進制表示“開關狀態”，通過?mask ^ (1 << i)?快速翻轉第?i?個開關的狀態，比數組操作更簡潔。

?
六、經典問題中的二進制應用

?
1.?子集和問題
當元素數量?n <= 20?時，可用二進制枚舉所有子集（?2^20 ≈ 1e6?），判斷是否存在和為目標值的子集。
?
2.?最大異或對
給定數組，找一對數使其異或結果最大。解法：按二進制位從高到低構建前綴樹（Trie），對每個數在樹中找能使異或最大的數（每一位盡量取相反值）。
?
3.?位運算dp
例如“統計[0, n]中數字二進制不含連續1的個數”，用dp記錄每一位的狀態（是否為1），通過位轉移避免連續1。
?
4.?格雷碼生成
格雷碼是相鄰數二進制僅差1位的編碼，生成公式：?gray(n) = n ^ (n >> 1)?，利用二進制異或特性直接構造。
?
總結
?
二進制在算法中的應用核心是利用位運算的高效性和二進制表示的結構性，實現從基礎操作到復雜問題的優化。無論是狀態壓縮、數據結構設計，還是數學問題求解，二進制都提供了簡潔且高效的思路，是算法工程師必須掌握的基礎工具。

七、實用的二進制運算技巧

n&(n-1)

將最低位的1置零

6&5 = 4 (110? 101? ->100)

n&(-n)

保留最低位的1，其余位清零

6&-6 = 2 (110)

n|(n-1)

將最低位的1及其右邊的位都置為1

6|5? =7 (110|101->111)

八、leetcode

九、算法講解030【必備】異或運算的騷操作

算法講解030【必備】異或運算的騷操作_嗶哩嗶哩_bilibilihttps://www.bilibili.com/video/BV1LN411z7nu/?spm_id_from=333.1387.collection.video_card.click&vd_source=cdc2a34485eb016f95eae1a314b1a6201.異或：無進位相加

不同為1，相同為0

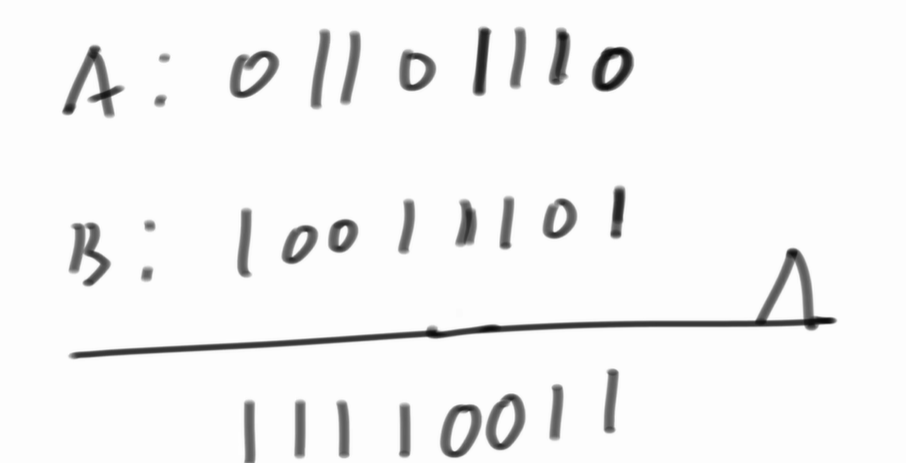
2.異或運算滿足交換律和結合律

3.0^a=a? ? ? n^n=0

4.

1^0^1^0=1

1^0=1

5.異或運算交換兩個數

a^=b;

b^=a;

a^=b;

6.不用任何判斷語句和比較操作，返回兩個數的最大值?

import mathdef get_max(a, b):return (a + b + math.fabs(a - b)) / 2

int max_with_xor(int a, int b) {int diff = a - b;// 獲取符號位（對于32位整數）int sign = (diff >> 31) & 1;// 使用異或計算最大值return a ^ (sign ^ (a ^ b));
}

無溢出版

int max_with_xor_safe(int a, int b) {// 計算符號位：a和b符號不同時為1，相同時為0int sign_diff = ((a ^ b) >> 31) & 1;// 當a和b符號不同時：// - 若a為正，則a大；若a為負，則b大int result1 = (a >> 31 & 1) ? b : a;// 當a和b符號相同時：// 使用異或方法（此時a-b不會溢出）int diff = a - b;int sign = (diff >> 31) & 1;int result2 = a ^ (sign ^ (a ^ b));// 根據符號是否相同選擇結果（利用異或的特性）return (sign_diff ? result1 : result2);
}

7.找到缺失的數字

原[0,1,2,4]

補全[0,1,2,3,4]

原的異或^補全的異或=缺失的數字

268. 丟失的數字 - 力扣（LeetCode）https://leetcode.cn/problems/missing-number/submissions/8.數組中一種數出現了奇數次，其他的數都出現了偶數次，返回出現了奇數次的數

閹割版

136. 只出現一次的數字 - 力扣（LeetCode）https://leetcode.cn/problems/single-number/submissions/654128520/9.找出數組中兩個出現偶數次的數

先全部異或得到a^b

取出最右側的1

之后樹狀數組也會用到

n&((~n)+1)=n&(-n)

Brian Kernighan算法

n&(n-1)

10.找唯一一個出現次數少于m次的數

看二進制的狀態

11.補充：

計算一個數的二進制表示中 1 的個數

class Solution {
public:// 計算n的二進制表示中1的個數int hammingWeight(int n) {int count = 0;// 當n不為0時，繼續循環while (n != 0) {// 清除最右邊的1n &= n - 1;// 計數加1count++;}return count;}
};

其他方法

int hammingWeight(int n) {int count = 0;for (int i = 0; i < 32; i++) {// 檢查第i位是否為1if ((n & (1 << i)) != 0) {count++;}}return count;
}