平衡二叉樹的定義
平衡二叉樹(balanced binary tree),又稱AVL樹(Adelson-Velskii and Landis)。 一棵平衡二叉樹或者是空樹,或者是具有下列性質的二叉排序樹:
① 左子樹與右子樹的高度之差的絕對值小于等于1;
② 左子樹和右子樹也是平衡二叉排序樹。 為了方便起見,給每個結點附加一個數字,給出該結點左子樹與右子樹的高度差。這個數字稱為結點的平衡因子(BF)。
平衡因子 = 結點左子樹的高度 - 結點右子樹的高度
根據平衡二叉樹的定義,平衡二叉樹上所有結點的平衡因子只能是-1、0,或1
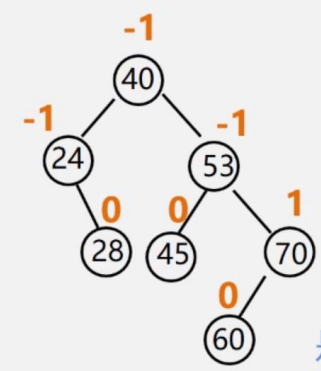
我們分析一下這個二叉樹
對于40,左子樹高度是2(看左子樹有幾層),右子樹高度是3,2-3=-1,所以40的平衡因子是-1,平衡
對于24,左子樹高度是0,對右子樹高度為1,0-1=-1,24的平衡因子是-1,以此類推
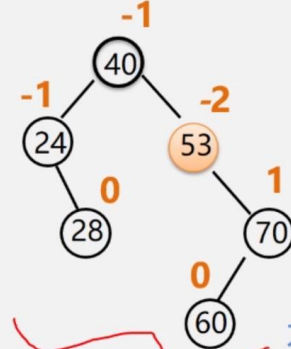
我們直接分析一下53,53的左子樹高度是0,右子樹高度是2,所以0-2=-2,失衡
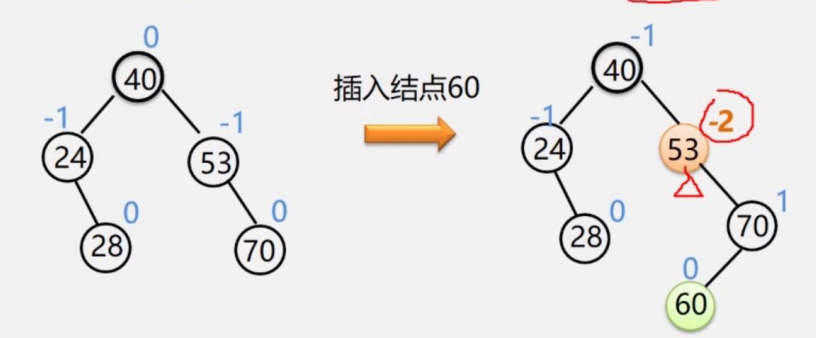
如果在一棵 AVL 樹中插入一個新結點后造成失衡,則必須重新調整樹的結構,使之恢復平衡。
平衡調整的四種類型:
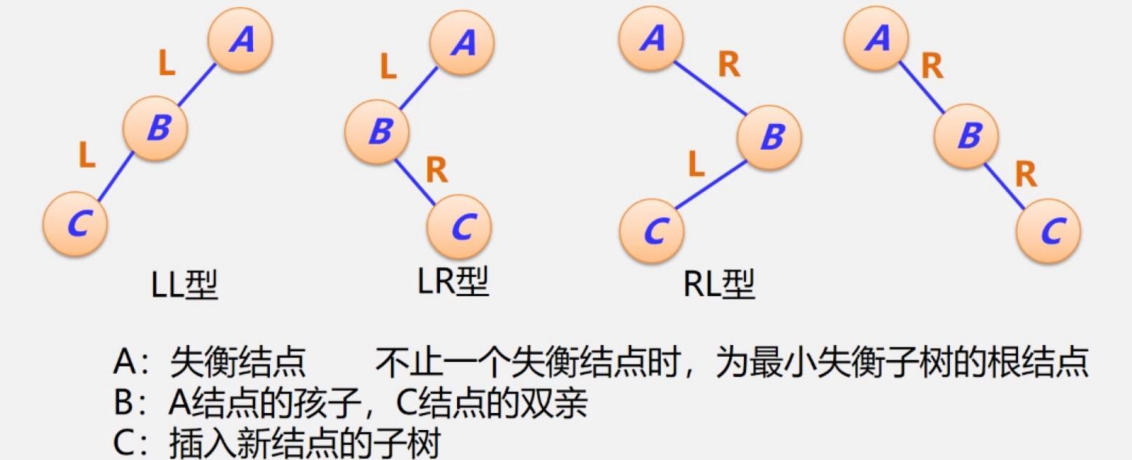
C表示的是插入的結點,怎么插入的分了上邊四種類型
調整原則:1)降低高度 2)保持二叉排序樹性質
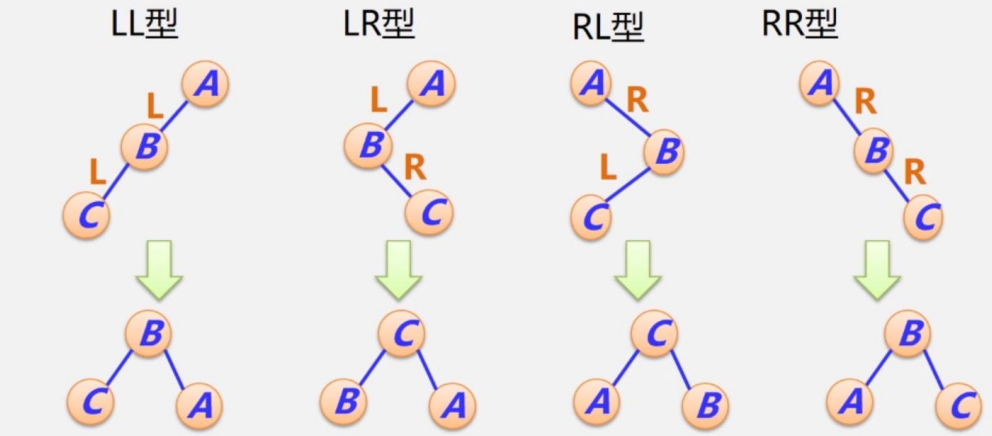
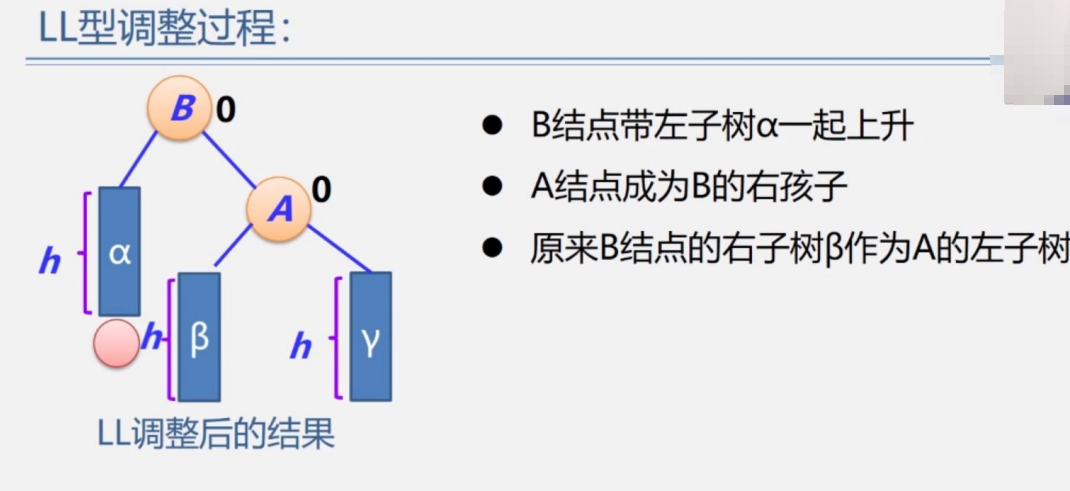
對于LL型的,對根節點進行順時針旋轉,RR型是根節點A逆時針旋轉
我們也可以通過平衡后要滿足二叉排序樹的性質,比如對上圖的LL型,C<B<A,所以調整的時候,根據左子樹小于根小于右子樹的性質,B作為根,C作為左子樹,A作為右子樹
對上圖的LR型,B<C<A,則C作為根節點,B作為左子樹,A作為右子樹
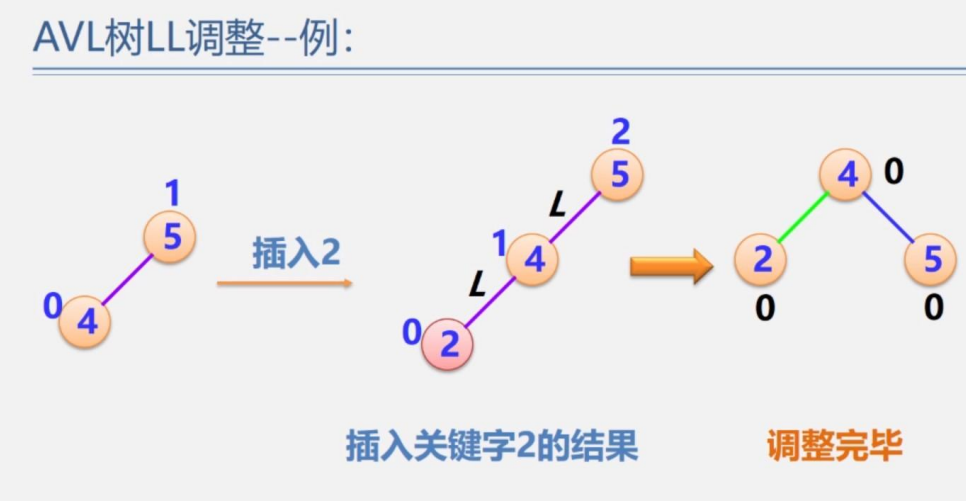
插入2,2比5小,在左子樹,2比4小,是4的左子樹,插入順序是LL型,發現失衡了,于是將根節點5順時針旋轉下來即可
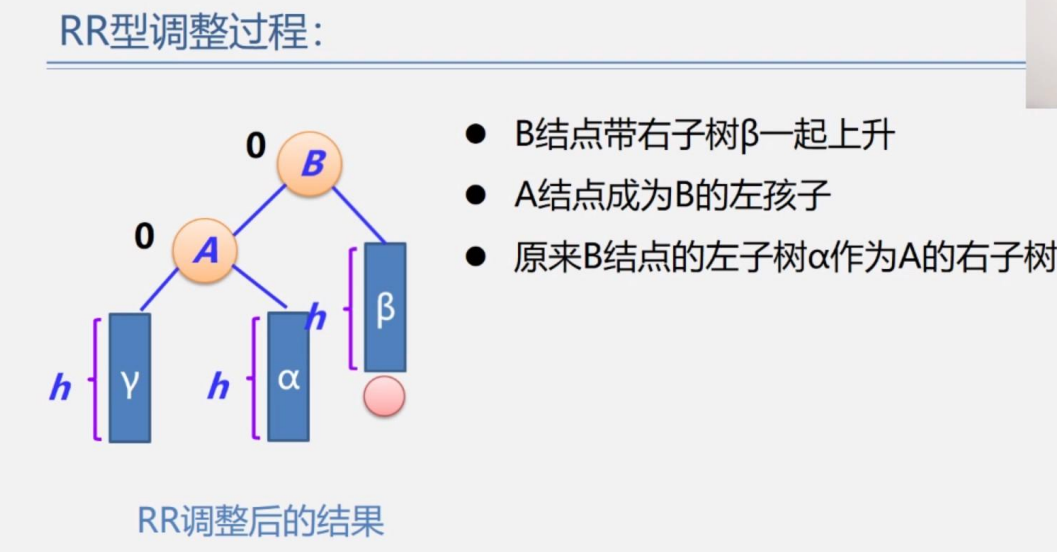
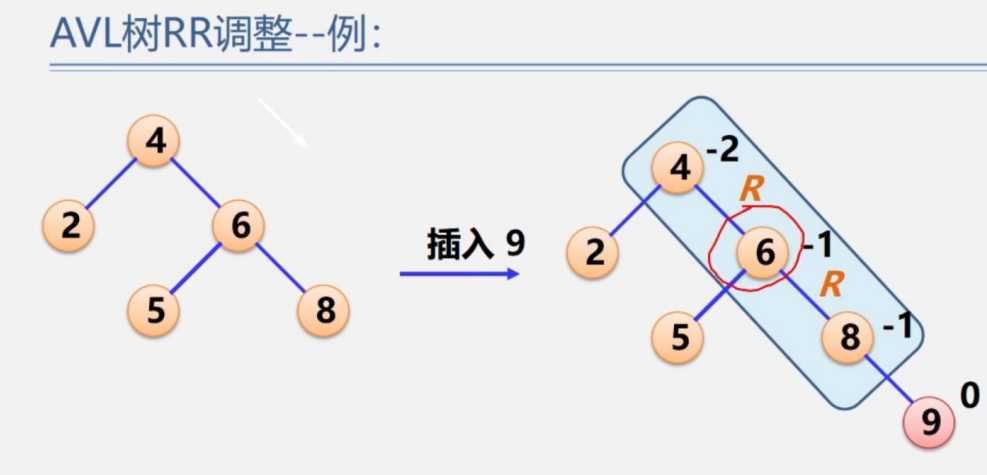
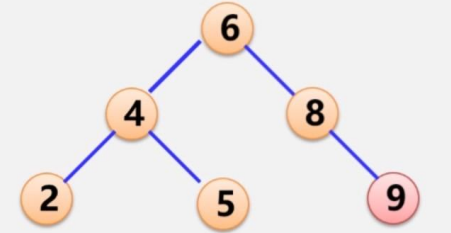
插入9,發現插入的是RR型,失衡了以后,將根節點4逆時針旋轉,即6作為根節點,4作為6的左子樹,而6的左子樹作為4的右子樹,也就是下圖:
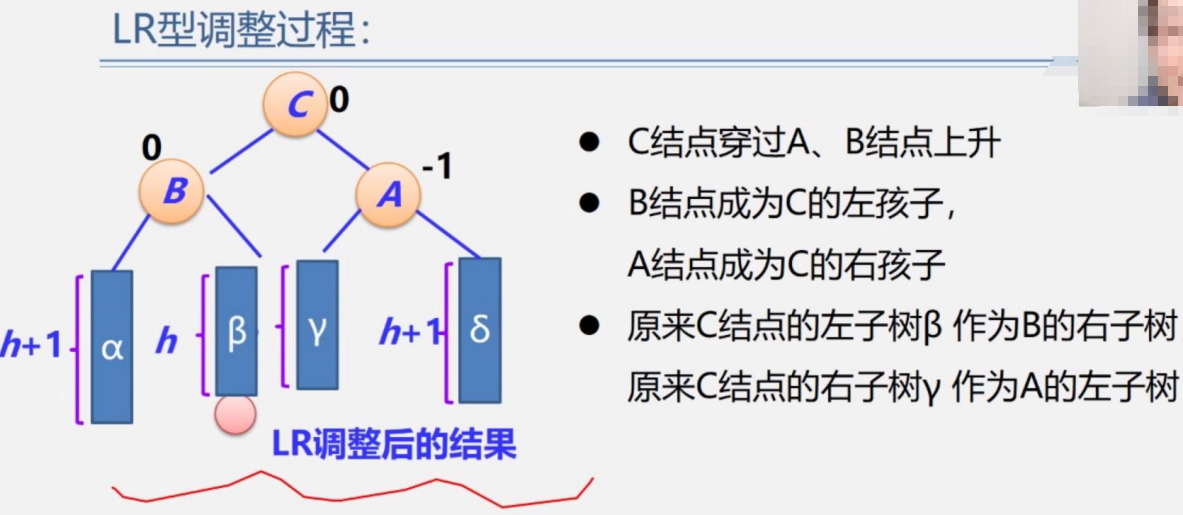
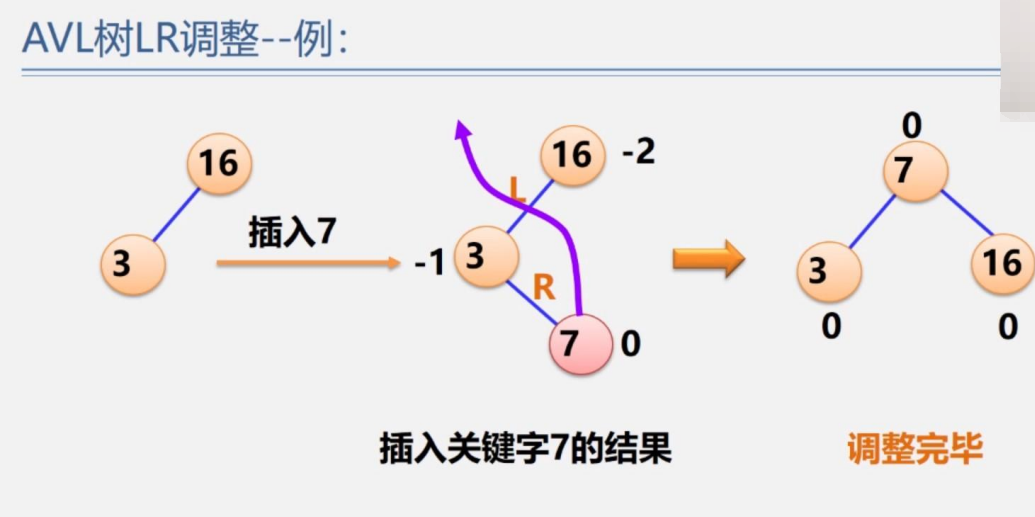
我們發現插入的類型是LR型,那么將葉子節點7升上去,作為根節點,然后3和16比較大小,小的3放入7的左子樹,大的16放入7的右子樹
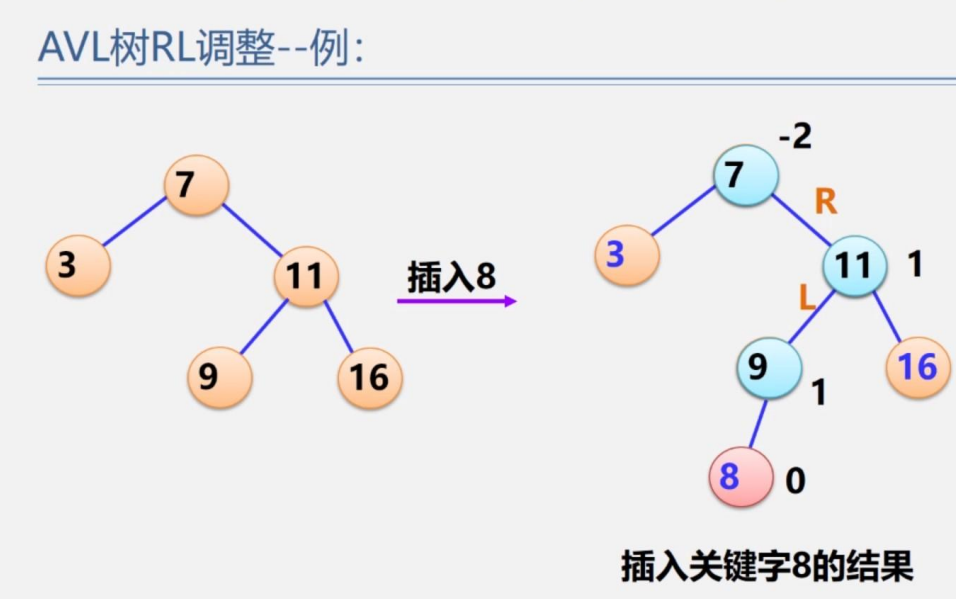
我們插入8,發現是RL型,將RL型的葉子節點9升上去,7作為9的左子樹,11作為9的右子樹,9原本的左子樹作為7的右子樹
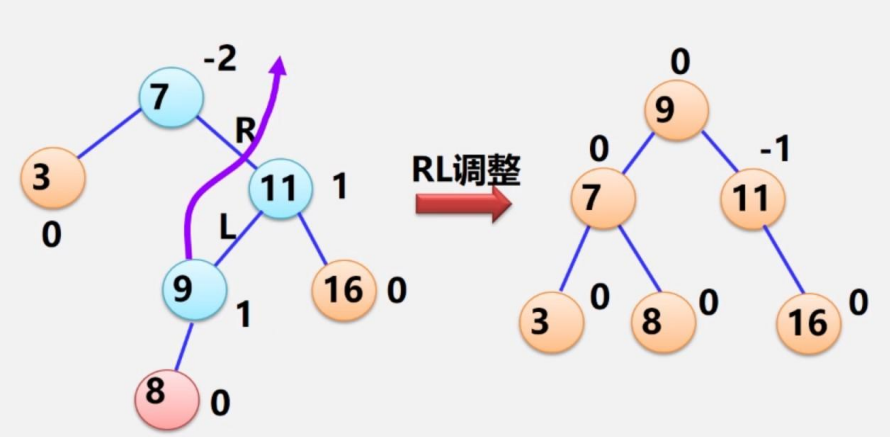










)




)



:ThemeResolver - 動態換膚的奧秘)