A Logical Calculus of the Ideas Immanent in Nervous Activity（神經網絡早期的M-P模型）

哈嘍，各位朋友大家上午好！今天我們要一起啃下這篇神經科學與邏輯學交叉領域的奠基之作——McCulloch和Pitts的《A Logical Calculus of the Ideas Immanent in Nervous Activity》。
在這里插入圖片描述

這篇論文篇幅不長，但每一個定理、每一個假設都像精密齒輪，共同構成了“神經活動可被邏輯描述”的核心框架。從最基礎的假設講起，逐個解析所有定理，對于大家關注的定理部分，會做深入拆解。

基本信息

論文標題: A LOGICAL CALCULUS OF THE IDEAS IMMANENT IN NERVOUS ACTIVITY*
作者與合著者: WARREN S. MCCULLOCH（美國伊利諾伊大學醫學院、伊利諾伊神經精神病學研究所精神病學系）、WALTER PITTS（美國芝加哥大學）
發表期刊 / 會議：最初發表于《Bulletin of Mathematical Biophysics》第 5 卷，第 115-133 頁，后重印于《Bulletin of Mathematical Biology》第 52 卷第 1/2 期，第 99-115 頁
發表時間: 1943 年（最初發表），1990 年（重印）
DOI/URL: https://doi.org/10.1007/BF02478259

一、引言：神經活動與邏輯的“相遇”

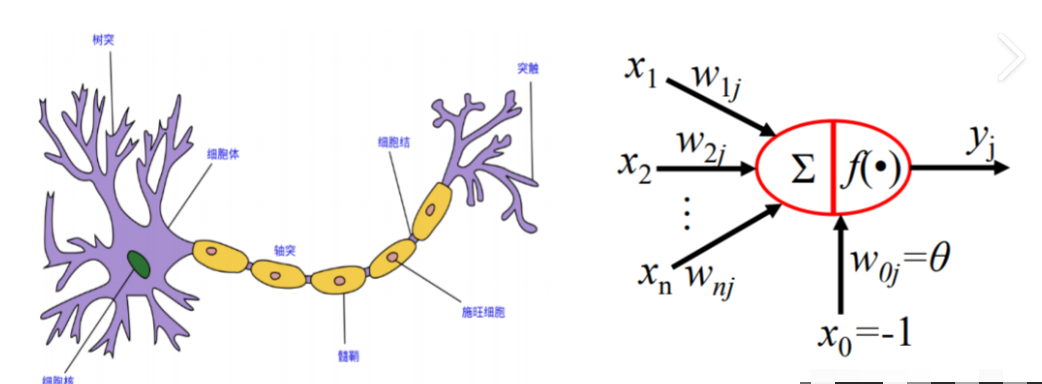
論文開篇就點明了核心洞察：神經元的“全或無”特性（要么興奮，要么不興奮），使得神經事件及其關系可以用命題邏輯處理，好比開關的“通”與“斷”對應邏輯的“真”與“假”，為整個理論埋下了伏筆。

同時，簡單網絡可用基礎邏輯描述，含循環的復雜網絡則需要更復雜的邏輯工具；反之，滿足特定條件的邏輯表達式，總能找到對應的神經網絡。

二、神經生理學的核心假設：理論的“地基”

要建立邏輯模型，必須先明確神經元的“行為規則”。作者提出了5個物理假設，這些是所有定理的前提：

全或無特性：神經元活動是“非此即彼”的過程，沒有中間狀態，對應命題的二值性（真/假）。
固定閾值：激發神經元需要“潛伏疊加期”（<0.25ms）內達到一定數量的興奮性突觸激活，這個數量不隨歷史或位置變化。比如，神經元A的閾值是3，就必須在0.25ms內有3個興奮性突觸同時被激活才能興奮。
突觸延遲是唯一顯著延遲：神經元內部的傳導延遲可忽略，只有突觸處有>0.5ms的延遲。這讓時間可以被離散化為“突觸延遲的整數倍”（t=0,1,2,…），方便用邏輯符號描述時間關系。
抑制性突觸的絕對作用：只要有抑制性突觸被激活，神經元就絕對不會興奮，對應邏輯中的“否定”（?）——抑制信號直接讓命題為假。
網絡結構不變：短期內不考慮學習導致的突觸變化，后續會用“循環網絡”模擬學習。

這些假設看似簡化了真實神經生理（比如實際神經元的閾值可能變化），但正是這種抽象讓邏輯建模成為可能。比如“突觸延遲”的設定，使得時間可以被量化為離散的“步長”，為后續的“時間命題表達式”奠定了基礎。

三、符號系統：神經活動的“邏輯語言”

要將神經活動轉化為邏輯，必須定義一套符號系統。作者借鑒了Carnap、羅素和懷特海的符號，構建了專屬語言：

神經元動作符號： $N_i(t)$ 表示“神經元 $c_i$ 在時間t（t為突觸延遲的整數倍）被激發”。比如 $N_1(2)$ 意為“神經元1在第2個突觸延遲時刻興奮”。
時間算子S： $S (P) (t)$ 等價于 $P (t ? 1)$ ，表示“前一個時間步的P狀態”。比如 $S(N_2)(t)$ 即 $N_2(t-1)$ ，描述了“神經元2在前一時刻的興奮狀態”。
邏輯連接符：使用∨（析取，“或”）、∧（合取，“與”）、?（否定，“非”）表示命題關系，與傳統邏輯一致。

該符號系統是“神經活動→邏輯表達式”的翻譯工具。比如，“神經元3在t時刻興奮，當且僅當神經元1在t-1時刻興奮，或神經元2在t-3時刻興奮且t-2時刻未興奮”，可寫成：
$N3(t)≡N1(t?1)∨(N2(t?3)∧?N2(t?2))N_3(t) \equiv N_1(t-1) \lor (N_2(t-3) \land \neg N_2(t-2))$ 。
在論文中對應于冷熱感知錯覺的例子，直觀展示了符號系統的用法。

四、時間命題表達式（TPE）：可被神經網絡實現的邏輯

并非所有邏輯表達式都能對應神經活動，作者定義了“時間命題表達式（TPE）”來框定范圍，其遞歸定義如下：

基礎形式：單個謂詞變量的時間函數 $p(z_1)$ （如 $N_i(t)$ ）是TPE。
復合形式：若 $S_1$ 和 $S_2$ 是含相同自由變量的TPE，則 $S(S_1)$ （前一時間的 $S_1$ ）、 $S_1∨S_2$ 、 $S_1∧S_2$ 、 $S_1∧?S_2$ 也是TPE。

即TPE是“能被神經網絡實現的邏輯表達式”，其核心是只能涉及過去或現在的狀態，不能預測未來，這與神經活動的因果性一致。

五、零階網絡（無循環）的定理：簡單邏輯與網絡的等價性

零階網絡是指沒有“循環路徑”（如A→B→C→A）的網絡，其行為最容易用TPE描述，在論文用3個定理建立了兩者的雙向關系。
在這里插入圖片描述

定理1：零階網絡的行為可用TPE描述

含義：任何無循環的神經網絡，其每個神經元的興奮規則都能寫成TPE。
證明思路：

對零階網絡中的神經元 $c_i$ ，設其閾值為 $βi\beta_i$ ，有 $p$ 個興奮性突觸來自 $c_{i1},...,c_{ip}$ ， $q$ 個抑制性突觸來自 $c_{j1},...,c_{jq}$ 。
其興奮條件為：
- ① 所有抑制性神經元在t-1時刻未興奮（ $∏m=1q?Njm(t?1)\prod_{m=1}^q \neg N_{jm}(t-1)$ ）；
- ② 興奮性神經元的某個子集的突觸數量之和超過閾值（ $∑α∈κi∏s∈αNis(t?1)\sum_{\alpha \in \kappa_i} \prod_{s \in \alpha} N_{is}(t-1)$ ，其中 $κi\kappa_i$ 是滿足條件的子集集合）。
結合時間算子S，可寫成： $Ni(t)≡S{∏m=1q?Njm(t)∧∑α∈κi∏s∈αNis(t)}N_i(t) \equiv S\left\{ \prod_{m=1}^q \neg N_{jm}(t) \land \sum_{\alpha \in \kappa_i} \prod_{s \in \alpha} N_{is}(t) \right\}$
由于網絡無循環，可通過“替換法”逐步消除非外周神經元（將其表達式代入其他神經元的規則），最終所有神經元的活動都能用外周神經元的TPE表示。

例：一個簡單的“與門”網絡（神經元C的閾值為2，接收A和B的興奮性突觸），其規則為 $NC(t)≡S(NA(t)∧NB(t))N_C(t) \equiv S(N_A(t) ∧ N_B(t))$ ，顯然是TPE。

定理2：任何TPE都能被零階網絡實現

含義：只要是TPE，就一定能設計出對應的無循環網絡。
證明思路：

基礎case：單個 $p(z_1)$ 可由單個神經元實現（外周神經元）。
復合case：
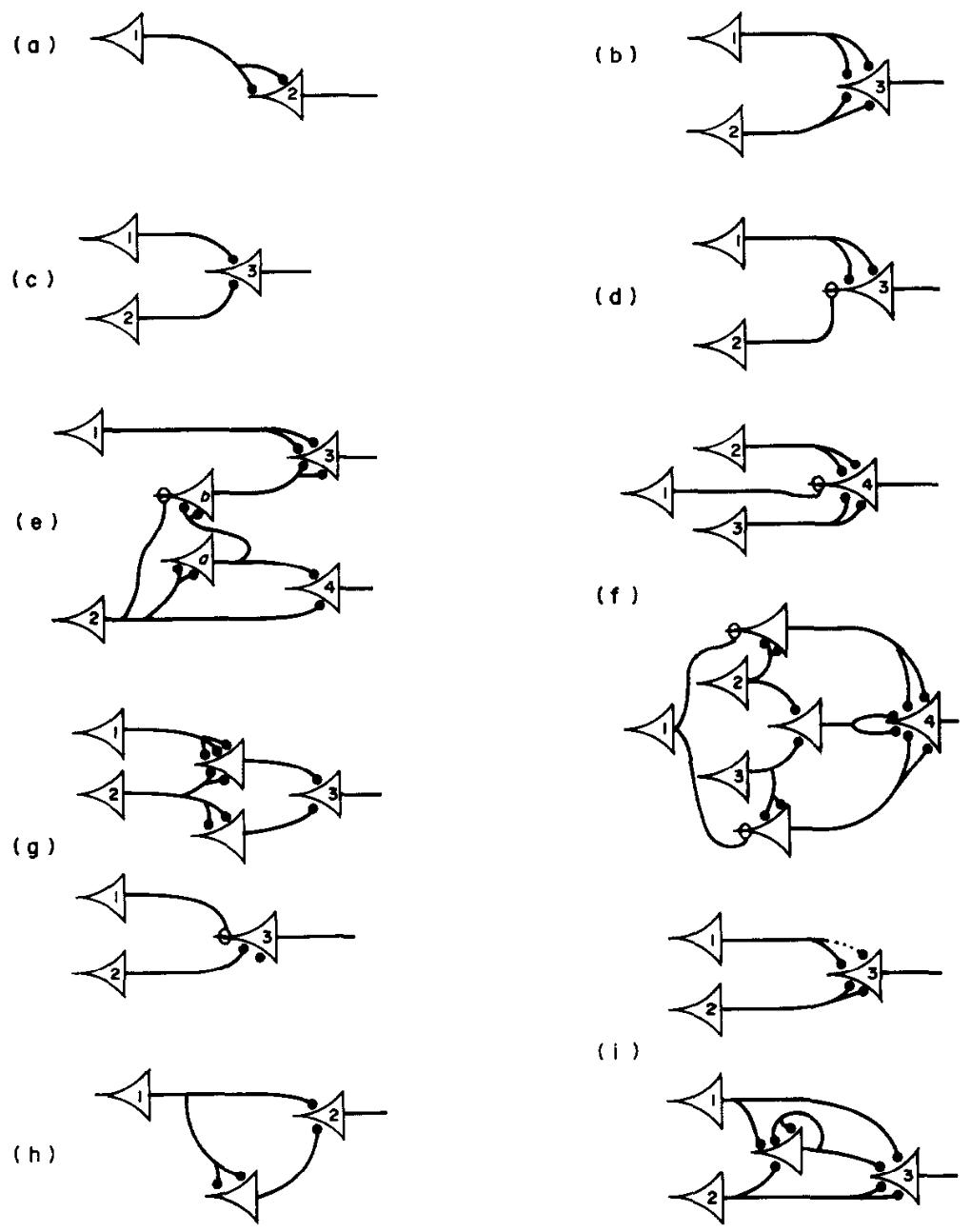
- $S(p_1)$ ：用一個神經元接收 $p_1$ 的突觸，延遲一個時間步輸出（圖1a）。
- $p_1∨p_2$ ：設計神經元，閾值為1，接收 $p_1$ 和 $p_2$ 的興奮性突觸（圖1b）。
- $p_1∧p_2$ ：設計神經元，閾值為2，接收 $p_1$ 和 $p_2$ 的興奮性突觸（圖1c）。
- $p_1∧?p_2$ ：設計神經元，閾值為1，接收 $p_1$ 的興奮性突觸和 $p_2$ 的抑制性突觸（圖1d）。
通過歸納法，所有TPE都可由這些基礎結構組合實現。

例：TPE“ $S(p_1) ∨ (p_2 ∧ ?p_3)$ ”可由“ $S(p_1)$ 的網絡”與“ $p_2 ∧ ?p_3$ 的網絡”通過“或門”組合而成。

定理3：TPE的判定條件

含義：一個邏輯表達式是TPE，當且僅當它滿足三個等價條件之一：

當所有 constituent $p(z_1-zz)$ 為假時，表達式為假；
其真值表最后一行（所有輸入為假）為“假”；
其希爾伯特析取范式中，沒有僅由否定項組成的項。

證明思路：

必要性：TPE由基礎形式通過∨、∧、?和S組合而成，當所有輸入為假時，復合表達式必為假（如 $S_1∨S_2$ 在 $S_1$ 和 $S_2$ 都假時為假）。
充分性：若表達式滿足條件3，可寫成 $S_1∧...∧S_m) ∧ ?(S_{m+1}∨...∨S_n)$ ，顯然是TPE。

例：“ $p \lor ? q$ ”不是TPE（當p和q都假時，表達式為真，違反條件1）；“ $p \land q$ ”是TPE（p和q都假時為假）。

六、等價性定理：不同神經機制的“邏輯等效”

神經生理存在多種可能機制（如抑制的方式、學習的實現），作者證明了它們在“擴展意義上等價”——即一種機制能實現的功能，另一種也能實現（可能時間不同）。

定理4：相對抑制與絕對抑制等價

相對抑制：抑制性突觸提高神經元閾值（如原本需3個興奮，1個抑制后需4個）。
絕對抑制：抑制性突觸直接阻止神經元興奮（只要有1個抑制，無論多少興奮都無效）。
等價性證明：
- 相對抑制的規則可寫成TPE（如“興奮數-抑制數>閾值”），而TPE可由零階網絡實現（定理2），其中絕對抑制可模擬相對抑制的效果（如用多個抑制性突觸抵消興奮性輸入）。
- 反之，絕對抑制也可通過相對抑制模擬（如設置足夠高的閾值，讓抑制后永遠無法達到）。

定理5：消退與絕對抑制等價

消退：神經元興奮后，閾值在一段時間內升高（如興奮后j個時間步，閾值+ $b_j$ ）。
等價性證明：
- 用M個循環網絡 $T1,...,TM\mathscr{T}_1,...,\mathscr{T}_M$ （分別含1,…,M個神經元）模擬消退：神經元 $c_i$ 興奮后，激活這些循環，每個循環在j個時間步后通過 $b_j$ 個抑制性突觸作用于 $c_i$ ，等效于閾值升高。
- 反之，絕對抑制也可通過消退模擬（如設置足夠大的 $b_j$ ）。

定理6：易化與時間總和可被空間總和替代

易化/時間總和：神經元對時間上分散的興奮（如t-2和t-1時刻的興奮）進行疊加。
等價性證明：
- 引入延遲鏈（含不同數量突觸的路徑），將時間上的興奮轉化為空間上的同步興奮（如t-2的興奮通過2個突觸延遲，t-1的興奮通過1個突觸延遲，最終在t時刻同步到達），從而用空間總和模擬時間總和。

定理7：可改變的突觸（學習）可被循環替代

可改變的突觸：原本無效的突觸，在“神經元興奮且突觸同時激活”后變為有效。
等價性證明：
- 用循環網絡模擬突觸變化：當神經元 $c_i$ 興奮且突觸前神經元 $c_j$ 激活時，激活一個循環路徑，使 $c_j$ 的信號持續作用于 $c_i$ ，等效于突觸變為有效。

七、高階網絡（含循環）的定理：處理“記憶”與遞歸

當網絡存在循環（如A→B→A），神經元活動會依賴“歷史狀態”（記憶），其行為需用遞歸函數描述。

定理8：循環網絡的解可通過遞歸表達式描述

含義：含循環的網絡（階數p）的行為，可通過含遞歸的表達式描述，其中神經元活動依賴于自身或其他神經元的過去狀態（可能是任意早的過去）。
證明思路：

設循環集為 $c_1,...,c_p$ ，其活動滿足 $Ni(t)≡Pri[Sni1N1(t),...,SnipNp(t)]N_i(t) \equiv Pr_i[S^{n_{i1}}N_1(t),...,S^{n_{ip}}N_p(t)]$ （ $Pr_i$ 為含外周輸入的表達式）。
通過反復代入，可將表達式轉化為依賴 $S^nN_j(t)$ （n為 $n_{ij}$ 的最小公倍數）的形式，再轉化為希爾伯特析取范式，最終用遞歸函數表示為：
$Ni(t)≡(E?)(x)t?1??(x)≤2p??(t)=i?P[?(x+1),?(x),N?(0)(0)]N_i(t) \equiv (E\phi)(x)_{t-1} \cdot \phi(x) \le 2^p \cdot \phi(t)=i \cdot P[\phi(x+1), \phi(x), N_{\phi(0)}(0)]$ 。
其中 $?\phi$ 是描述歷史狀態序列的函數，體現了“記憶”的作用。

定理9：可實現類（prehensible classes）的判定條件

含義：一個類的函數能被神經網絡實現，當且僅當它滿足特定的遞歸條件（涉及邏輯運算和時間算子的封閉性）。
證明思路：

基于前面的符號和定理，可實現類需對邏輯運算（?、∧、∨）和時間算子S封閉，且能通過有限步驟遞歸定義。

定理10：集合K的所有成員均可實現

集合K的定義：
1. 任何TPE，以及用K中成員替換TPE的變元后仍屬于K；
2. 若 $Pr1(z1)∈KPr_1(z_1)\in K$ ，則 $z_2)_{z_1}Pr_1(z_2)$ （全稱量詞）、 $Ez_2)_{z_1}Pr_1(z_2)$ （存在量詞）、 $C_{mn}(z_1)$ （模n同余m）也屬于K。
證明：通過歸納法，K中的成員均可通過循環網絡實現（如用循環網絡實現量詞和模運算）。

八、神經網絡與圖靈機的等價性

論文最后指出：神經網絡的計算能力與圖靈機等價。

任何圖靈機能計算的數，配備“紙帶、掃描儀、效應器”的神經網絡都能計算；
神經網絡能計算的數，圖靈機也能計算；
含循環的神經網絡可在無紙帶時計算部分數，但范圍不超過圖靈機。

這一結論將神經活動與“可計算性”理論綁定，為“認知即計算”的思想提供了早期依據。

九、研究思路總結

該論文的研究思路堪稱“從現象到理論”的典范，可拆解為四步：

現象抽象：從神經元“全或無”“突觸延遲”等特性中，提煉出與二值邏輯的相似性，將神經活動映射為命題。
符號建模：定義 $N_i(t)$ 、S算子等符號，構建“神經活動→邏輯表達式”的翻譯系統，明確TPE的范圍。
雙向驗證：
- 正向：證明零階網絡的行為能被TPE描述（定理1），高階網絡的行為能被遞歸表達式描述（定理8）；
- 反向：證明TPE和更復雜的表達式（集合K）能被對應網絡實現（定理2、10）。
等價擴展：證明不同神經機制（抑制、消退、學習等）在邏輯功能上等價，拓寬理論的適用范圍（定理4-7）。

該“觀察→抽象→建模→驗證→擴展”的框架體現了跨學科研究的核心方法論。其核心觀點在于：面對復雜的生物系統，研究者無需在初始階段過度關注細節，而應通過合理的抽象化過程提取關鍵規律，進而運用邏輯與數學工具構建具有普適性的理論模型。本研究的學術價值不僅體現在為神經網絡奠定了理論基礎，更在于通過嚴謹的邏輯推演揭示了生命現象的內在機制——此類研究范式可為多領域學術探索提供方法論借鑒。