目錄
一.什么是樸素貝葉斯
1.1 從 “概率” 到 “分類”
二.樸素貝葉斯的數學基礎:貝葉斯定理
2.1 貝葉斯定理公式
2.2 從貝葉斯定理到樸素貝葉斯分類
2.3 “樸素” 的關鍵:特征獨立性假設
三、樸素貝葉斯的三種常見類型
3.1 高斯樸素貝葉斯(Gaussian Naive Bayes)
3.2 多項式樸素貝葉斯(Multinomial Naive Bayes)
3.3 伯努利樸素貝葉斯(Bernoulli Naive Bayes)
四、樸素貝葉斯的工作流程
步驟 1:數據準備與預處理
步驟 2:計算先驗概率P(C)
步驟 3:計算似然概率P(x_i|C)
步驟 4:預測新樣本
五、樸素貝葉斯的優缺點
優點:
缺點:
改進方向:
六、樸素貝葉斯的經典應用場景
1. 文本分類
2. 推薦系統
3. 醫療診斷
4. 欺詐檢測
七.案例實訓
1.鳶尾花分類
2.數字識別
一.什么是樸素貝葉斯
樸素貝葉斯是一種基于貝葉斯定理和特征獨立性假設的分類算法。它的核心思想是:通過已知的 “先驗概率”,結合數據特征計算 “后驗概率”,最終以 “后驗概率” 最大的類別作為預測結果。
1.1 從 “概率” 到 “分類”
生活中充滿了概率決策的場景:比如看到烏云密布(特征),我們會判斷 “下雨(類別)的概率更高”;收到一封含 “優惠”“點擊鏈接” 的郵件(特征),我們會推測 “這是垃圾郵件(類別)的概率更高”。樸素貝葉斯做的正是類似的事 —— 通過特征推斷類別,本質是概率驅動的分類。
它的 “樸素” 體現在對特征的假設上:假設所有特征之間相互獨立。這個假設雖然簡化了計算,但在實際場景中(比如文本分類)往往能得到不錯的結果,這也是它 “樸素卻實用” 的原因。
二.樸素貝葉斯的數學基礎:貝葉斯定理
2.1 貝葉斯定理公式
貝葉斯定理的數學表達式如下: P(A|B) = P(B|A)P(A)/P(B)
其中:
- P(A|B):后驗概率,指在已知 “事件 B 發生” 的條件下,“事件 A 發生” 的概率(這是我們最終要計算的目標);
- P(B|A):似然概率,指在 “事件 A 發生” 的條件下,“事件 B 發生” 的概率;
- P(A):先驗概率,指 “事件 A 發生” 的概率(在沒有任何證據時,對 A 的初始信念);
- P(B):邊緣概率,指 “事件 B 發生” 的概率(作為歸一化常數,不影響類別判斷的相對大小)。
2.2 從貝葉斯定理到樸素貝葉斯分類
在分類問題中,我們需要用特征推測類別。假設輸入特征為X=(x_1, x_2, ..., x_n)(比如郵件中的關鍵詞),類別為C(比如 “垃圾郵件” 或 “正常郵件”),則樸素貝葉斯的核心公式可改寫為:
P(C∣X)=P(X∣C)/P(C)/p(X)?
其中:
- P(C|X):后驗概率,即 “已知特征 X 時,屬于類別 C 的概率”(我們要最大化的目標);
- P(C):先驗概率,即 “類別 C 在所有數據中出現的概率”(比如垃圾郵件占總郵件的比例);
- P(X|C):似然概率,即 “在類別 C 中,特征 X 出現的概率”(比如垃圾郵件中出現 “優惠” 關鍵詞的概率);
- (P(X):邊緣概率,對所有類別都相同,計算時可忽略。
2.3 “樸素” 的關鍵:特征獨立性假設
直接計算P(X|C)并不容易,因為特征X可能有多個維度(比如文本有多個關鍵詞)。樸素貝葉斯通過 “特征獨立性假設” 簡化計算:假設特征(x_1, x_2, ..., x_n)相互獨立,則:
P(X|C) = P(x_1|C)P(x_2|C)...P(x_n|C)
即 “聯合概率等于邊緣概率的乘積”。這個假設大幅降低了計算復雜度,讓樸素貝葉斯能高效處理高維數據(比如文本的詞向量)。
三、樸素貝葉斯的三種常見類型
根據特征數據的類型不同,樸素貝葉斯衍生出了三種常用模型,分別適用于不同場景:
3.1 高斯樸素貝葉斯(Gaussian Naive Bayes)
適用場景:特征是連續型數據(如身高、體重、鳶尾花的花瓣長度)。 核心思想:假設在每個類別下,特征服從高斯分布(正態分布)。即對于類別C和特征(x_i),P(x_i|C)服從高斯分布(N(\mu_{C,i}, \sigma^2_{C,i})\),其中\(\mu\)是均值,\(\sigma^2\)是方差。
計算時,先通過訓練數據計算每個類別下各特征的均值和方差,再用高斯概率密度函數計算\(P(x_i|C)\)。
3.2 多項式樸素貝葉斯(Multinomial Naive Bayes)
適用場景:特征是離散計數數據(如文本中詞的出現次數、商品的點擊次數)。 核心思想:假設特征的分布服從多項式分布。例如在文本分類中,特征是 “詞頻”,則\(P(x_i|C)\)表示 “在類別C的文檔中,第i個詞出現的概率”。
為了避免 “零概率問題”(某個詞在類別C中從未出現過,導致\(P(x_i|C)=0\),乘積結果為 0),通常會使用拉普拉斯平滑(Laplace Smoothing),公式為: \(P(x_i|C) = \frac{count(x_i, C) + 1}{count(C) + n}\) 其中\(count(x_i, C)\)是特征\(x_i\)在類別C中的計數,\(count(C)\)是類別C的總計數,n是特征總數。
3.3 伯努利樸素貝葉斯(Bernoulli Naive Bayes)
適用場景:特征是二進制數據(0 或 1,如文本中詞是否出現、用戶是否點擊某個按鈕)。 核心思想:假設特征服從伯努利分布(即只有 “出現” 或 “不出現” 兩種狀態)。例如在文本分類中,特征是 “詞是否存在”(1 表示存在,0 表示不存在),則\(P(x_i|C)\)是 “類別C中詞i出現的概率”。
它同樣會使用拉普拉斯平滑處理零概率問題,且更關注 “特征是否出現” 而非 “出現次數”,適合短文本場景。
四、樸素貝葉斯的工作流程
樸素貝葉斯的訓練和預測流程非常簡潔,核心是 “統計概率” 和 “計算后驗”,具體步驟如下:
步驟 1:數據準備與預處理
- 收集帶標簽的訓練數據(特征X?+ 類別C);
- 對特征進行預處理:連續特征歸一化(高斯樸素貝葉斯)、離散特征編碼(多項式 / 伯努利)。
步驟 2:計算先驗概率P(C)
- 統計每個類別在訓練集中的占比:P(C) = 類別C的樣本數 / 總樣本數。
步驟 3:計算似然概率P(x_i|C)
- 根據特征類型選擇模型(高斯 / 多項式 / 伯努利),統計每個類別下各特征的概率分布:
- 高斯模型:計算每個類別下特征的均值和方差;
- 多項式 / 伯努利模型:統計特征在類別中的計數,并用平滑處理零概率。
步驟 4:預測新樣本
- 對新樣本的特征X=(x_1, x_2, ..., x_n),計算每個類別的后驗概率P(C|X)?
- 選擇后驗概率最大的類別作為預測結果。
五、樸素貝葉斯的優缺點
優點:
- 計算高效:訓練時只需統計概率,預測時是簡單的乘法運算,時間復雜度低,適合大規模數據;
- 適合高維數據:對文本等稀疏高維特征友好,無需降維也能表現良好;
- 數據需求少:少量樣本即可訓練(尤其先驗概率已知時);
- 可解釋性強:結果可通過概率解釋,比如 “該郵件是垃圾郵件的概率為 92%”。
缺點:
- 特征獨立性假設局限:實際中特征往往不獨立(比如 “暴雨” 和 “洪水” 相關),可能影響精度;
- 對特征分布敏感:若實際分布與假設分布(如高斯分布)偏差大,效果會下降;
- 難以學習特征間的交互關系:無法捕捉 “特征 A 且特征 B” 的聯合影響。
改進方向:
- 半樸素貝葉斯:放松獨立性假設,允許部分特征相關(如通過 “特征選擇” 保留重要關聯);
- 核函數擴展:對非獨立特征用核函數映射到高維空間,間接捕捉關聯。
六、樸素貝葉斯的經典應用場景
樸素貝葉斯憑借高效和實用性,在多個領域大放異彩:
1. 文本分類
- 場景:垃圾郵件過濾、新聞主題分類(科技 / 娛樂)、情感分析(正面 / 負面評價);
- 原理:將文本拆分為詞袋特征,用多項式 / 伯努利樸素貝葉斯計算 “詞特征屬于某類別的概率”。
2. 推薦系統
- 場景:基于用戶歷史行為推薦商品 / 電影;
- 原理:用用戶特征(年齡、性別)和物品特征(類型、價格)預測 “用戶喜歡該物品的概率”。
3. 醫療診斷
- 場景:根據癥狀(特征)判斷患病類型(類別);
- 原理:結合醫學先驗知識(疾病發病率\(P(C)\))和癥狀概率\(P(癥狀|疾病)\)做推斷。
4. 欺詐檢測
- 場景:信用卡盜刷、交易欺詐識別;
- 原理:通過交易金額、地點、時間等特征,計算 “該交易為欺詐的概率”。
七.案例實訓
1.鳶尾花分類
數據內容如下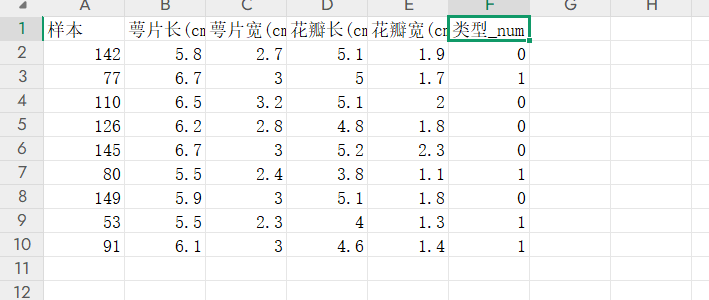
完整代碼如下:
需要注意我們可以將訓練內容無關的第一列內容樣本號刪除
# 鳶尾花分類
from sklearn import metrics
from sklearn.naive_bayes import MultinomialNB
import pandas as pd
data = pd.read_excel('鳶尾花測試數據.xlsx')
data=data.drop('樣本',axis=1)
X=data.iloc[:,:-1]
y=data.iloc[:,-1]ml=MultinomialNB()
ml.fit(X,y)
predicted=ml.predict(X)
print(ml.score(X,y))
print(metrics.classification_report(y,predicted))2.數字識別
我們可以使用sklearn中自帶的數據集,這里我們用自帶的數據集load_digits完成手寫數字識別
完整代碼如下
# 手寫數字識別分類
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
digits=load_digits()
X=digits.data
y=digits.target
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.3,random_state=0)
ml.fit(train_x,train_y)
print('===============自測報告==============')
self_predicted=ml.predict(train_x)
print(metrics.classification_report(train_y,self_predicted))
print('===============測試報告==============')
test_predicted=ml.predict(test_x)
print(metrics.classification_report(test_y,test_predicted))===============自測報告==============precision recall f1-score support0 1.00 0.98 0.99 1331 0.88 0.76 0.82 1302 0.92 0.90 0.91 1243 0.99 0.88 0.93 1294 0.96 0.96 0.96 1335 0.98 0.87 0.92 1256 0.98 0.97 0.97 1217 0.91 0.98 0.94 1268 0.73 0.88 0.80 1139 0.77 0.87 0.82 123accuracy 0.91 1257macro avg 0.91 0.91 0.91 1257
weighted avg 0.91 0.91 0.91 1257===============測試報告==============precision recall f1-score support0 0.98 0.98 0.98 451 0.88 0.81 0.84 522 0.94 0.87 0.90 533 1.00 0.81 0.90 544 0.96 0.96 0.96 485 0.98 0.82 0.90 576 0.97 1.00 0.98 607 0.88 0.98 0.93 538 0.89 0.90 0.89 619 0.71 0.93 0.80 57accuracy 0.91 540macro avg 0.92 0.91 0.91 540
weighted avg 0.92 0.91 0.91 540????????
)





:端口無權限)
線性方程組解的結構)

 這樣的 Controller 方法)









