一、機器學習概述
機器學習(Machine Learning, ML)是人工智能的核心分支,旨在通過算法讓計算機從數據中自動學習規律并優化性能,而無需顯式編程。這一技術領域起源于20世紀50年代,隨著計算能力的提升和大數據時代的到來,在21世紀得到了迅猛發展。
1. 基本概念
機器學習通過數據訓練模型,使其能夠識別模式、做出預測或決策。與傳統編程不同,機器學習系統不是通過直接編寫規則,而是通過分析大量數據來"學習"如何完成任務。
2. 核心思想
其核心是"從經驗中自動改進",這一思想模仿了人類的學習過程。機器學習系統通過不斷調整內部參數,逐步提高在特定任務上的表現。
3. 關鍵三要素
機器學習的實現依賴于三大基本要素:
- 數據:訓練材料,包括結構化數據(如數據庫表格)和非結構化數據(如文本、圖像)
- 模型:輸入到輸出的映射函數,如決策樹、神經網絡等
- 算法:優化方法如梯度下降、隨機梯度下降等
機器學習算法分類
1. 監督學習(Supervised Learning)
監督學習使用標注數據訓練模型,需要提供輸入數據和對應的正確輸出(標簽)。主要應用包括:
分類:預測離散類別
- 垃圾郵件識別(二分類)
- 手寫數字識別(多分類)
- 醫療影像診斷(如識別腫瘤類型)
回歸:預測連續數值
- 房價預測(基于面積、位置等特征)
- 股票價格預測
- 銷售預測
常用算法:
- 線性回歸
- 邏輯回歸
- 支持向量機(SVM)
- 決策樹
- 隨機森林
2. 無監督學習(Unsupervised Learning)
無監督學習從無標簽數據中發現隱藏的結構和模式。主要應用包括:
聚類:
- K-Means:客戶細分、文檔分類
- 層次聚類:生物學的物種分類
- DBSCAN:異常檢測
降維:
- 主成分分析(PCA):數據可視化、特征提取
- t-SNE:高維數據可視化
- 自編碼器:圖像壓縮
關聯規則學習:
- 購物籃分析(啤酒與尿布)
- 推薦系統
3. 強化學習(Reinforcement Learning)
強化學習通過環境交互學習最優策略,其核心是"試錯學習"。主要特點包括:
應用場景:
- 游戲AI(AlphaGo、星際爭霸AI)
- 機器人控制(行走、抓取)
- 自動駕駛決策
- 金融交易策略
關鍵概念:
- 智能體(Agent)
- 環境(Environment)
- 獎勵(Reward)
- 策略(Policy)
算法分類:
- 基于價值的方法(Q-Learning)
- 基于策略的方法(Policy Gradients)
- Actor-Critic方法
機器學習庫
在Python中進行機器學習開發時,Scikit-learn是最常用的機器學習庫之一。它提供了各種監督學習和無監督學習算法,以及數據預處理、模型評估等工具,是機器學習入門和實踐的最佳選擇
pip install scikit-learn ==1.0.2 -i https://pypi.tuna.tsinghua.edu.cn/simple
#篇使用版本為1.0.2
#導入方法如下
import sklearn二、KNN(K-Nearest Neighbors,K近鄰)算法
1.核心思想?
KNN是一種基于實例的監督學習算法,其核心假設是“相似的數據點在特征空間中彼此靠近”。通過計算待預測樣本與訓練集中所有樣本的距離,選擇最近的K個鄰居,根據這些鄰居的類別(分類任務)或數值(回歸任務)進行預測。本篇以分類為主。
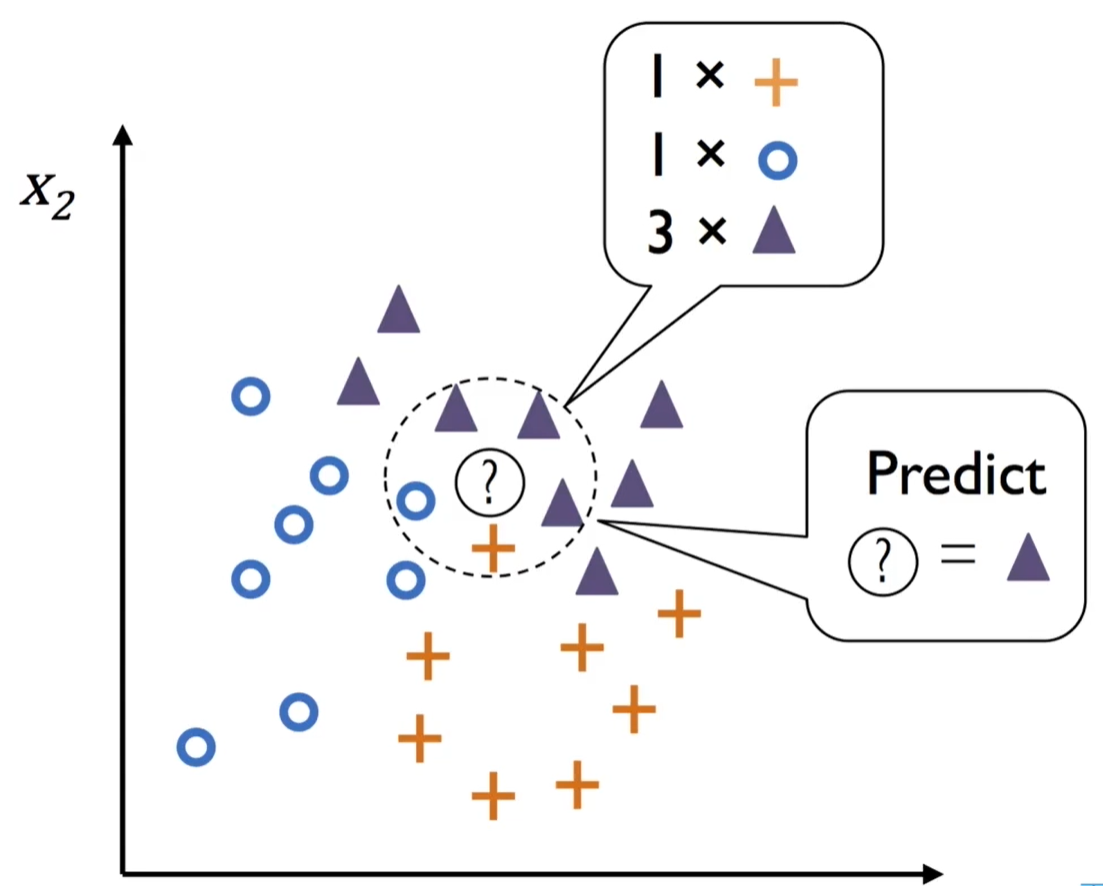
算法步驟?
數據準備
標準化/歸一化特征:消除量綱差異對距離計算的影響(如使用StandardScaler)
- 詳細步驟:
- 計算每個特征的均值(μ)和標準差(σ)
- 對每個特征值x進行變換:(x-μ)/σ
- 示例:若特征A的范圍是0-1000,特征B的范圍是0-1,標準化后兩個特征都服從均值為0、標準差為1的分布
- 應用場景:當特征的單位不同(如身高cm vs 體重kg)或數值范圍差異較大時
距離計算
常用距離度量:
歐氏距離(默認):適用于連續特征
- 公式:d(x,y)=√(∑(x_i-y_i)^2)
- 幾何解釋:兩點在n維空間中的直線距離
- 示例:在二維空間中,點(1,3)和(4,7)的距離為√((1-4)^2 + (3-7)^2)=5
曼哈頓距離:適用于網格路徑數據
- 公式:d(x,y)=∑|x_i-y_i|
- 別稱:城市街區距離
- 適用場景:棋盤格移動、城市道路規劃等網格狀路徑系統
- 示例:在二維網格中,(1,3)到(4,7)的距離為|1-4| + |3-7|=7
選擇K個最近鄰
按距離排序,選取前K個樣本
- 關鍵步驟:
- 計算待分類樣本與所有訓練樣本的距離
- 將所有距離按從小到大排序
- 選擇距離最小的K個樣本
- 注意事項:K值通常取奇數(如3/5/7)以避免平票情況
投票決策
統計K個鄰居的類別頻率,將待分類樣本劃入頻率最高的類別
- 具體流程:
- 統計K個鄰居中每個類別出現的次數
- 選擇出現次數最多的類別作為預測結果
- 平票處理:可隨機選擇或考慮更小的K值
- 擴展:也可使用加權投票,距離近的鄰居投票權重更大
數據準備
標準化/歸一化特征:消除量綱差異對距離計算的影響(如使用StandardScaler)
- 詳細步驟:
- 計算每個特征的均值(μ)和標準差(σ)
- 對每個特征值x進行變換:(x-μ)/σ
- 示例:若特征A的范圍是0-1000,特征B的范圍是0-1,標準化后兩個特征都服從均值為0、標準差為1的分布
- 應用場景:當特征的單位不同(如身高cm vs 體重kg)或數值范圍差異較大時
距離計算
常用距離度量:
歐氏距離(默認):適用于連續特征
- 公式:
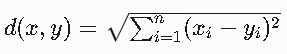
- 幾何解釋:兩點在n維空間中的直線距離
- 示例:在二維空間中,點(1,3)和(4,7)的距離為√((1-4)^2 + (3-7)^2)=5
曼哈頓距離:適用于網格路徑數據
- 公式:
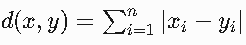
- 別稱:城市街區距離
- 適用場景:棋盤格移動、城市道路規劃等網格狀路徑系統
- 示例:在二維網格中,(1,3)到(4,7)的距離為|1-4| + |3-7|=7
選擇K個最近鄰
按距離排序,選取前K個樣本
- 關鍵步驟:
- 計算待分類樣本與所有訓練樣本的距離
- 將所有距離按從小到大排序
- 選擇距離最小的K個樣本
- 注意事項:K值通常取奇數(如3/5/7)以避免平票情況
投票決策
統計K個鄰居的類別頻率,將待分類樣本劃入頻率最高的類別
- 具體流程:
- 統計K個鄰居中每個類別出現的次數
- 選擇出現次數最多的類別作為預測結果
- 平票處理:可隨機選擇或考慮更小的K值
- 擴展:也可使用加權投票,距離近的鄰居投票權重更大
關鍵參數與優化??
關鍵參數與優化
K值選擇
K值的選擇直接影響KNN模型的性能:
- K值過小(如K=1):
- 模型會過于關注局部噪聲點,導致過擬合
- 決策邊界變得非常復雜且不規則
- 示例:在圖像分類中,K=1可能導致對個別異常像素過于敏感
- K值過大:
- 模型會忽略數據的局部特征,導致欠擬合
- 決策邊界過度平滑,可能錯過重要模式
- 示例:在房價預測中,過大的K值可能使不同社區的房價差異被平均化
優化方法:
- 交叉驗證:
- 采用k折交叉驗證(如5折或10折)評估不同K值
- 網格搜索:系統性地測試K值范圍(如1-20)
- 經驗法則:
- K≈√n(n為訓練樣本數)
- 通常選擇奇數K值以避免平票情況
- 對于分類問題,初始可嘗試K=3,5,7等小值
三、knn算法的運用
class sklearn.neighbors.KNeighborsClassifier( n_neighbors=5, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
參數名 | 類型/選項 | 默認值 | 作用 |
|---|---|---|---|
| int | 5 | 近鄰數K,決定投票的樣本數量 |
|
|
| 權重分配方式: |
|
|
| 近鄰搜索算法: |
| int | 2 | 閔可夫斯基距離的冪參數: |
| str或可調用對象 |
| 距離度量標準(如 |
| int或None | None | 并行計算線程數( |
法名 | 功能 | 示例 |
|---|---|---|
| 存儲訓練數據(惰性學習) |
|
| 返回預測類別 |
|
| 返回樣本屬于各類別的概率(基于鄰居類別的頻率) |
|
| 計算準確率(分類)或R2分數(回歸) |
|
| 返回K近鄰的索引和距離 |
|
四、算法示例
from matplotlib import pyplot as plt
import numpy as np#knn算法預測
from sklearn.neighbors import KNeighborsClassifier
data = np.loadtxt('datingTestSet2.txt', delimiter='\t')
neigh = KNeighborsClassifier(n_neighbors=5)
x=data[:800,:-1]
y=data[:800,-1]
neigh.fit(x,y)
print(neigh.score(x,y))#準確率,自測
c1=data[800:,:-1]
c2=data[800:,-1]
right=neigh.score(c1,c2)
print(right)
![]()

)



架構中,SoC(系統級芯片)與FPGA(現場可編程門陣列)之間的數據交互)
DFS)










)

