目錄

一、共現矩陣

1.1?基于共現矩陣的詞向量

二、SVD分解

2.1?基于共現矩陣的詞向量 vs. Word2Vec詞向量

三、GloVe詞向量

3.1 GloVe詞向量的好處

3.2 GloVe的一些結果展示

---

部分筆記來源參考

Beyond Tokens - 知乎 (zhihu.com)

NLP教程(1) - 詞向量、SVD分解與Word2Vec (showmeai.tech)

一、共現矩陣

1.1?基于共現矩陣的詞向量

先來回顧一下上節的Word2Vec的核心思想：讓相鄰的詞的向量表示相似。

我們實際上還有一種更加簡單的思路——使用「詞語共現性」，來構建詞向量，也可以達到這樣的目的。即，我們直接統計哪些詞是經常一起出現的，那么這些詞肯定就是相似的。那么，每一個詞，都可以做一個這樣的統計，得到一個共現矩陣（word-word co-occurrence matrix）。

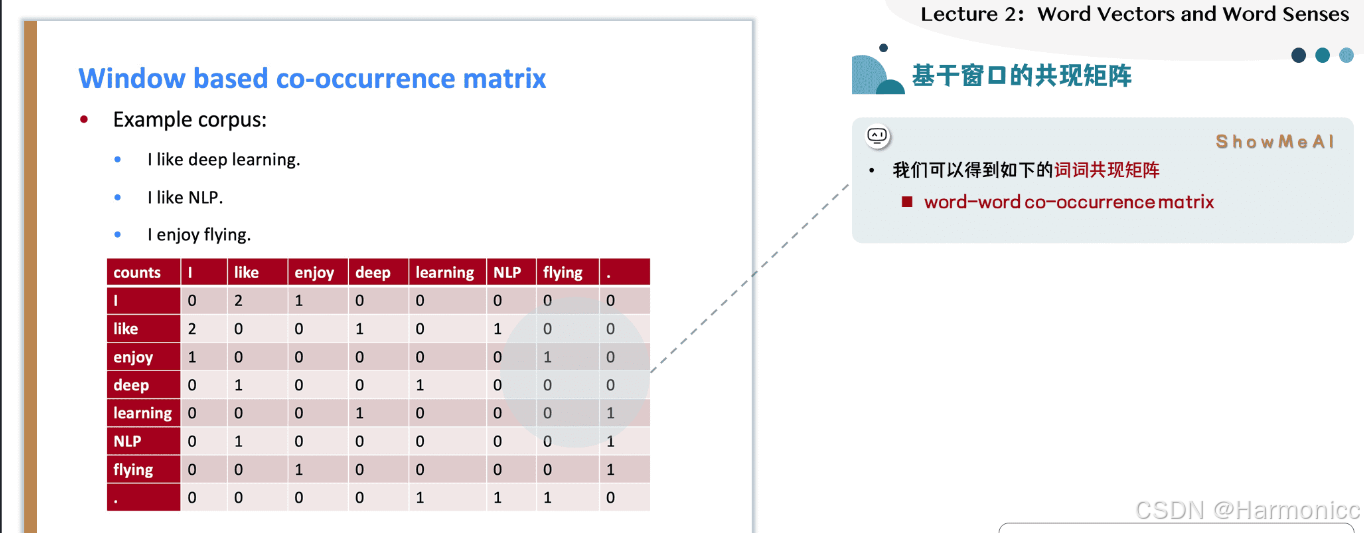
上面的例子中，給出了三句話，假設這就是我們全部的語料。我們使用一個size=1的窗口，對每句話依次進行滑動，相當于只統計緊鄰的詞。這樣就可以得到一個共現矩陣。

共現矩陣的每一列，自然可以當做這個詞的一個向量表示。這樣的表示明顯優于one-hot表示，因為它的每一維都有含義——共現次數，因此這樣的向量表示可以求詞語之間的相似度。

直接基于共現矩陣構建詞向量，會有一些明顯的問題，如下：

怎么解決這個問題呢？這就引出了我們第二節要講的SVD矩陣分解。

二、SVD分解

我們將巨大的共現矩陣進行SVD分解后，只選取最重要的幾個特征值，得到每一個詞的低維表示，從而解決維度問題，講到這里了，順便講講SVD的數學原理。

它可以將任意一個實數矩陣 分解成三個特殊矩陣的乘積，如下：

?

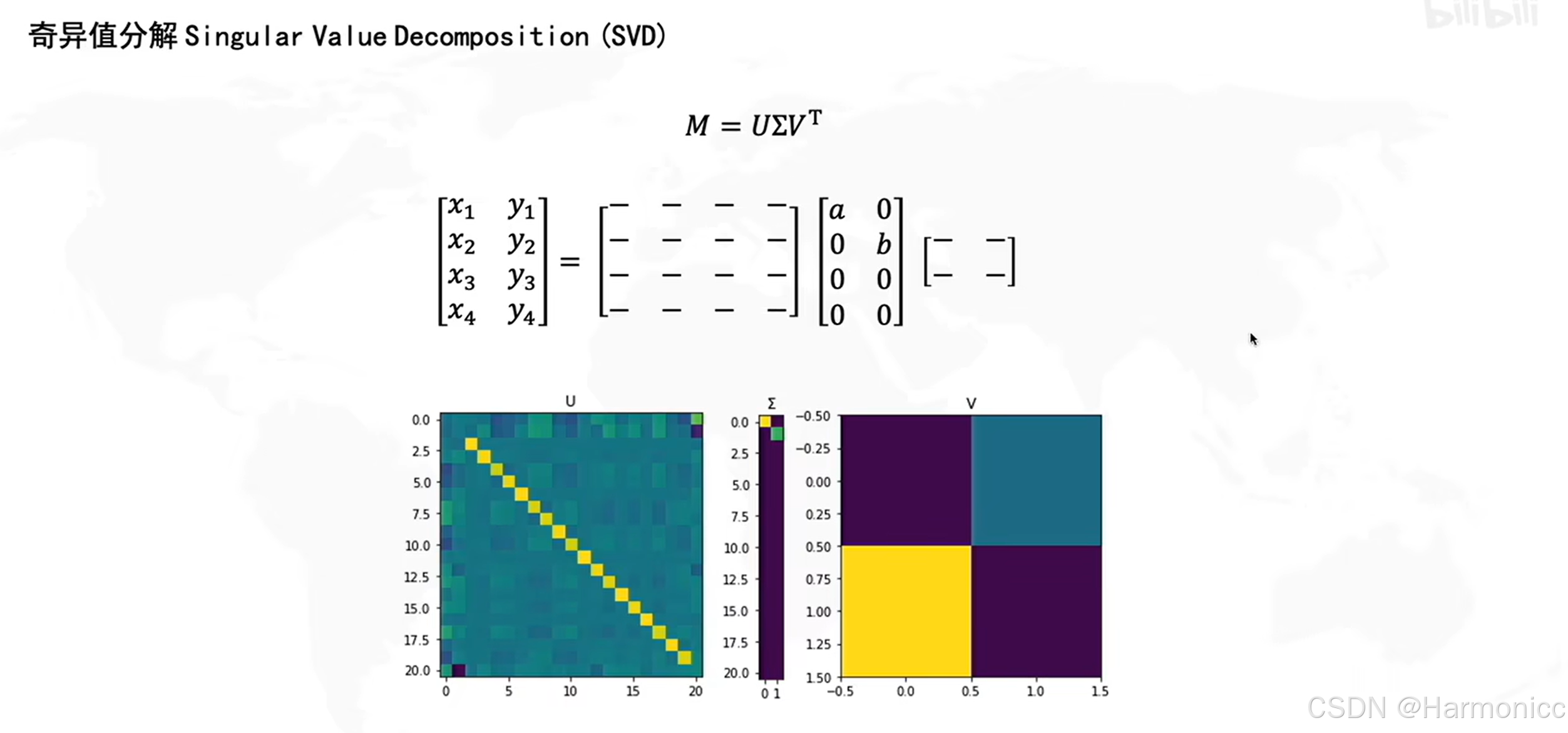從幾何的意義很好理解，記是一個線性變換，即對一個向量從的空間旋轉（）、拉伸（）、再旋轉（）到的空間，如下：

?

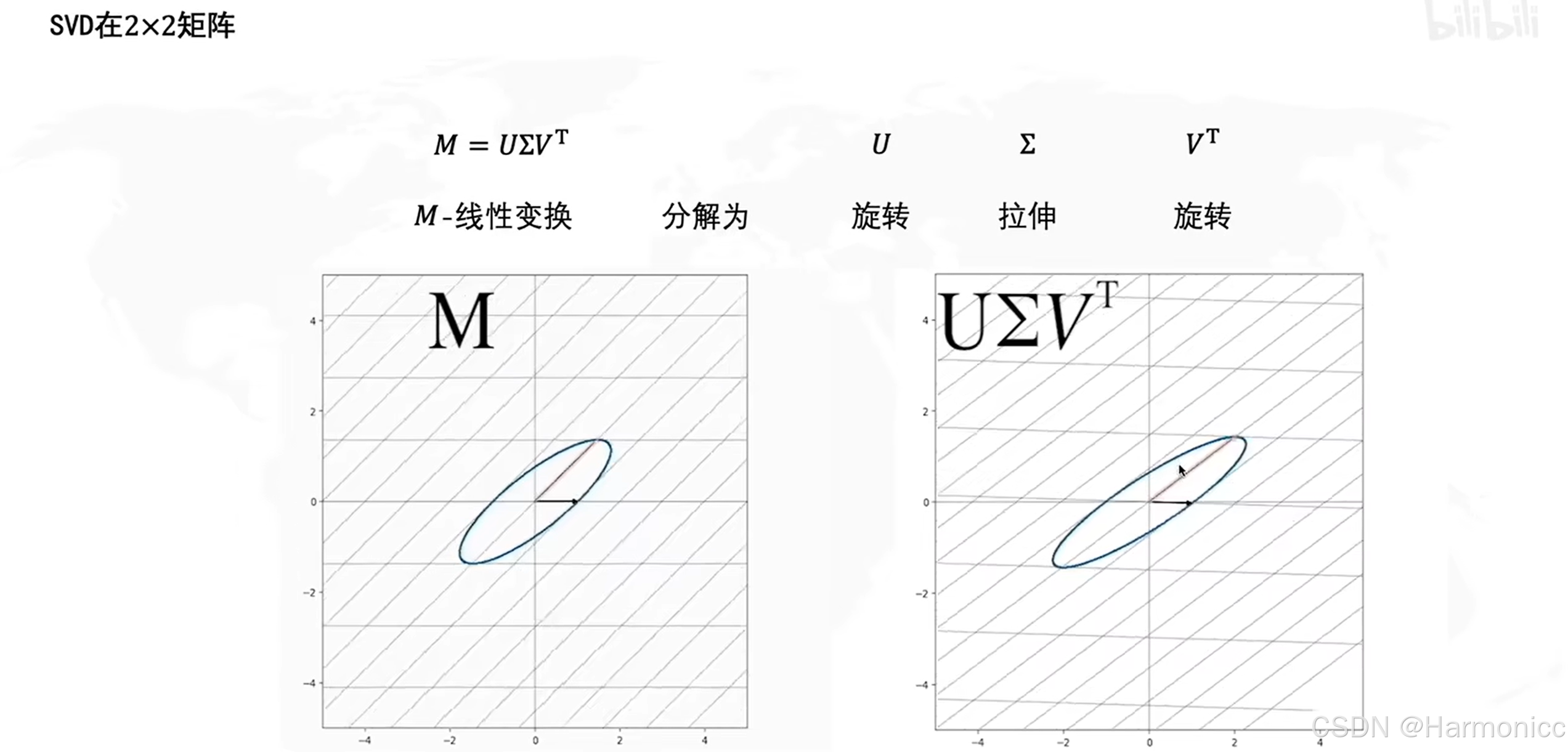從幾何的意義上，具體的原理如下：

?

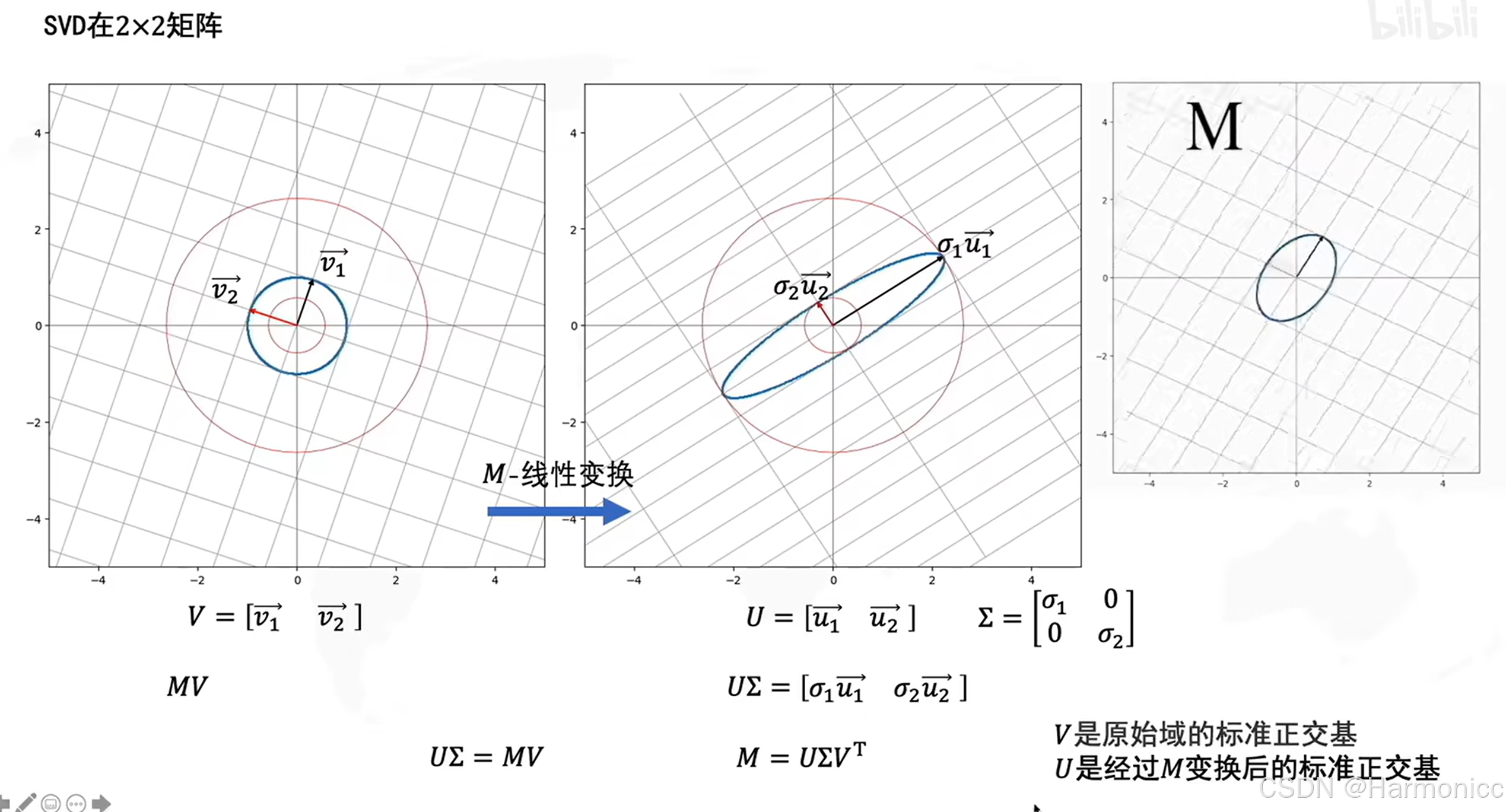而經過數次迭代后可以整理成我們想要得到的樣子

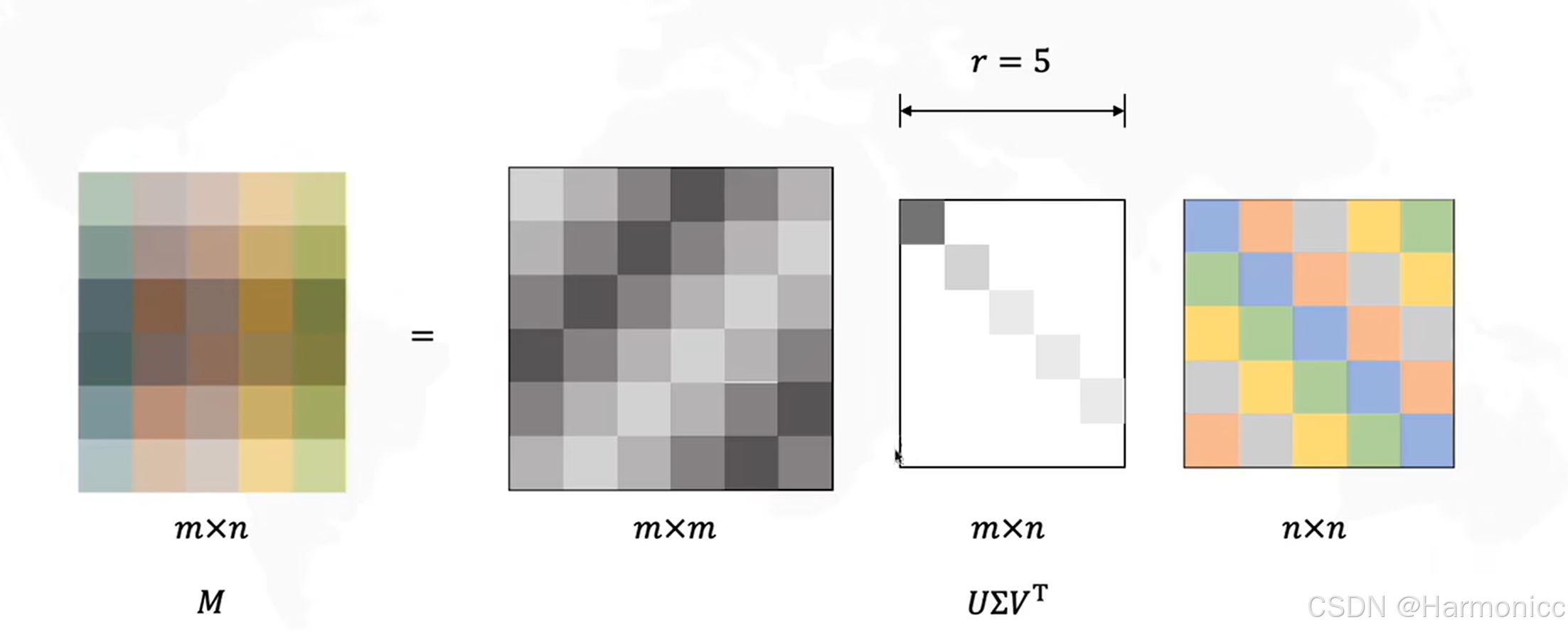
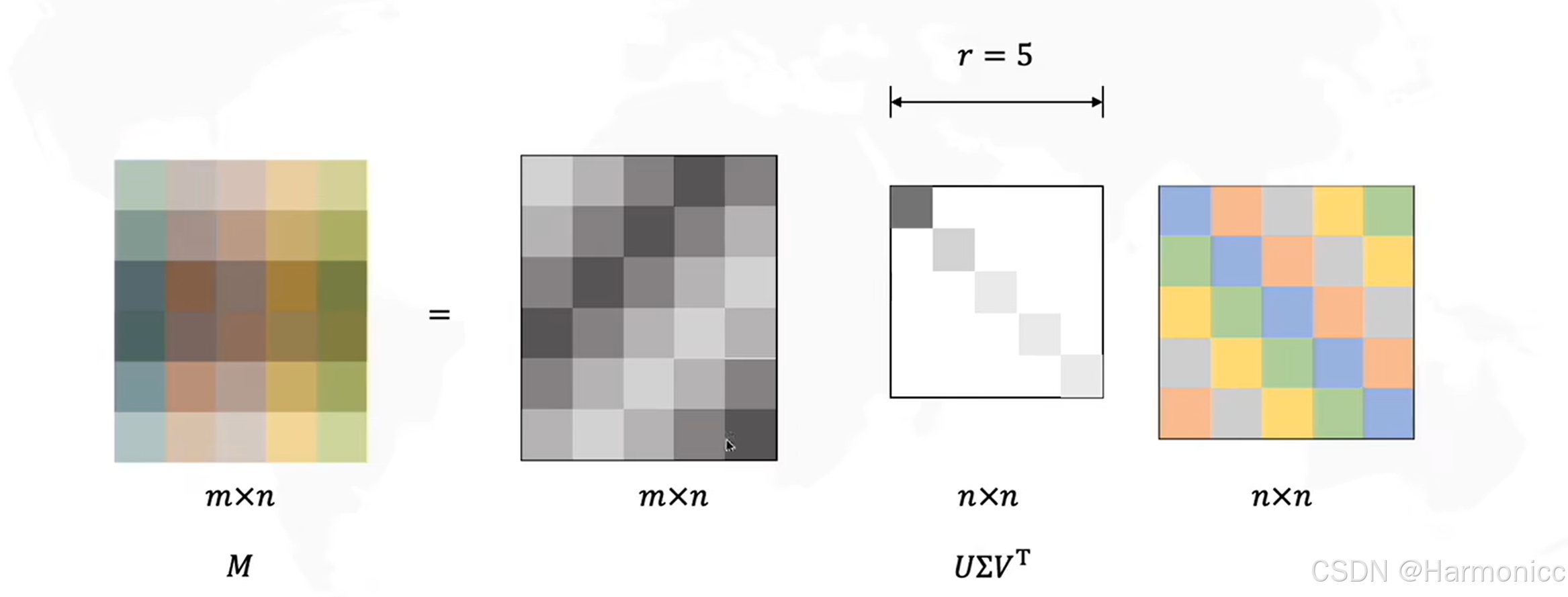
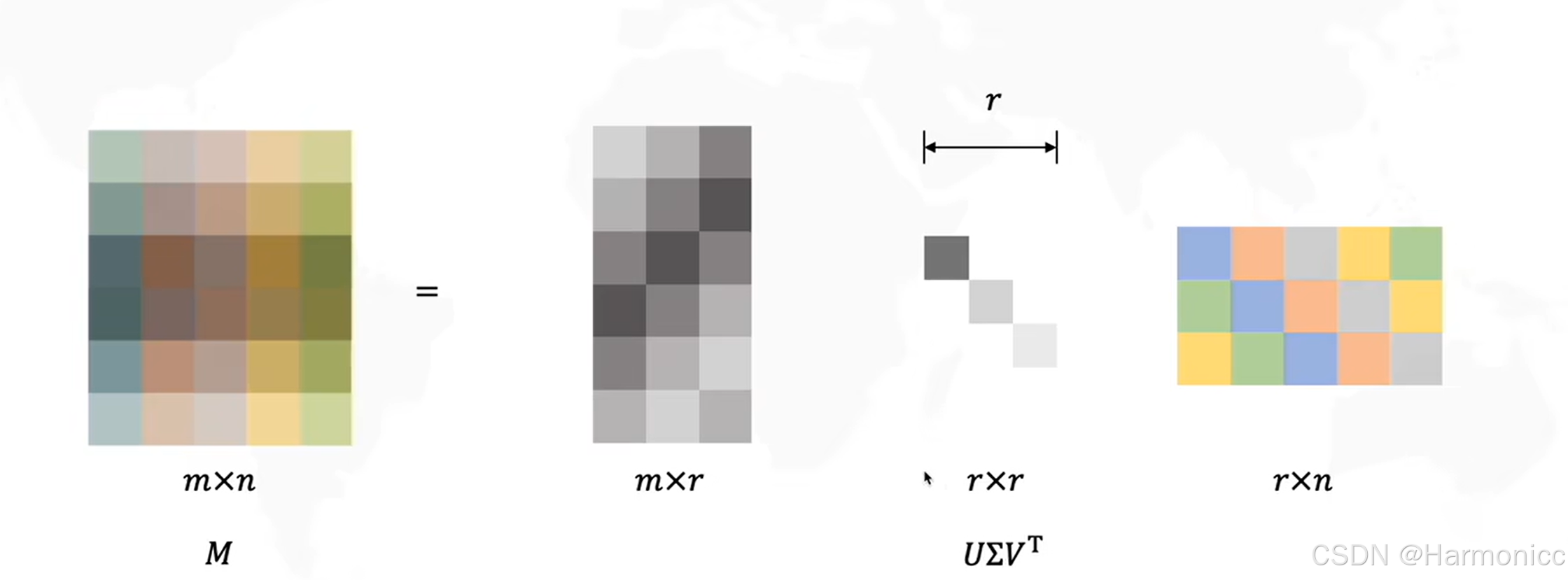
我們通過構建共現矩陣、進行SVD降維，可視化，依然呈現出了類似Word2Vec的效果。

但是還有一些問題，由于共現矩陣巨大，SVD分解的計算代價也是很大的。另外，像a、the、is這種詞，與其他詞共現的次數太多，也會很影響效果。所以，我們需要使用很多技巧，來改善這樣的詞向量。例如，直接把一些常見且意義不大的詞忽略掉；把極度不平衡的計數壓縮到一個范圍；使用皮爾遜相關系數，來代替共現次數等等很多技巧。

2.1?基于共現矩陣的詞向量 vs. Word2Vec詞向量

三、GloVe詞向量

這里我們采用第一種

我們和Word2vec的loss函數（下圖）對比一下，會發現這里loss的分母沒有顯式出現，這是因為分母已通過 Softmax 中的歸一化項隱式包含在中。

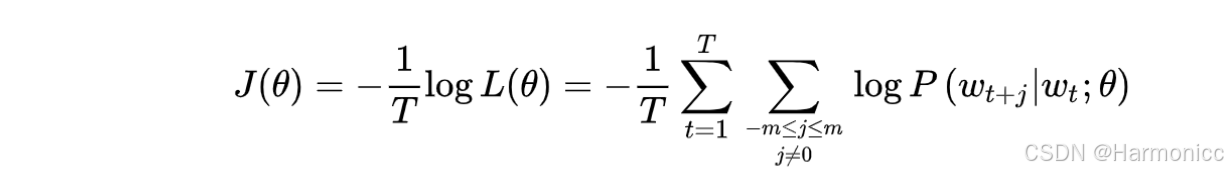
其實就是一個新的交叉熵函數。交叉熵，只是眾多損失函數中的一種，而交叉熵損失函數天然有一些缺陷：由于它是處理兩個分布，而很多分布都具有「長尾」的性質，這使得基于交叉熵的模型常常會給那些不重要、很少出現的情形給予過高的權重。另外，由于我們需要計算概率，所以「必須進行合理的規范化」（normalization），規范化，就意味著要除以一個「復雜的分母」，像Softmax中，我們需要遍歷所有的詞匯來計算分母，這樣的開銷十分巨大。

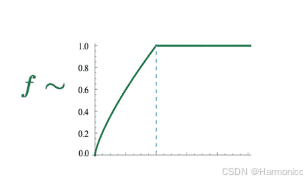
至此，我們得到了GloVe的損失函數（一套詞向量版）：

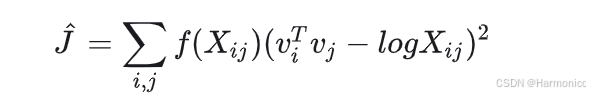
3.1 GloVe詞向量的好處

3.2 GloVe的一些結果展示

本小節結束