?一·參數
邏輯回歸參數及多分類策略等完整解析
LogisticRegression 初始參數聲明
LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='liblinear', max_iter=100, multi_class='ovr', verbose=0, warm_start=False, n_jobs=1)核心參數與概念詳細說明
- Penalty:正則化方式,含 L1、L2 ;newton - cg、sag、lbfgs 僅支持 L2 ,L1 假設參數服從拉普拉斯分布,L2 假設服從高斯分布,加約束理論增強泛化能力防過擬合 。
- Dual:對偶方法,用于線性多核(liblinear)的 L2 懲罰項;樣本數>特征數時,通常設 False 。
- Tol:迭代停止精度(容許停止標準 ),float 型,默認 1e - 4 。
- C:正則化強度,為正則化系數 λ 的倒數,數值越小正則化越強(類 SVM ),默認 1.0 (正浮點型數 )。
- fit_intercept:控制是否加截距項到決策函數,默認 True(加截距項 b )。
- intercept_scaling:僅正則化項為 “liblinear” 且 fit_intercept=True 時生效,float 型,默認 1 。
- class_weight:分類權重設置,支持字典、'balanced' ;默認 None(不考慮權重 ),樣本失衡時可用,“balanced” 按樣本量算權重(樣本多則權重低 ),也可自定義(如 {0:0.9,1:0.1} ),解決誤分類代價高、樣本失衡問題 。
- random_state:偽隨機數種子,用于數據洗牌,僅 sag、liblinear 正則化算法生效 。
- Solver:優化算法,可選 {‘newton - cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’} ,默認 liblinear :
- liblinear:坐標軸下降法,適小數據集;多分類用 OvR 策略,僅支持 L2 正則化(newton - cg、sag、lbfgs 同 ),saga 支持 L1/L2 ;
- newton - cg:牛頓法,二階泰勒展開減迭代輪數,需算 Hessian 矩陣逆(復雜度高 );
- lbfgs:擬牛頓法,近似 Hessian 矩陣逆,解決牛頓法求逆難題;
- Sag:隨機平均梯度下降,一階優化,用部分樣本算梯度,適大數據集(>10 萬 ),不支持 L1 ;
- Saga:線性收斂隨機優化算法變種,通吃 L1/L2 。
- max_iter:算法最大迭代次數,int 型,默認 100 ;僅 newton - cg、sag、lbfgs 正則化算法生效 。
- multi_class:分類策略,可選 ovr(one - vs - rest )、multinomial(many - vs - many ),默認 ovr :
- OvR:多元轉二元處理,第 K 類樣本為正例,其余為負例做二元回歸,遍歷類別構建模型;相對簡單,分類效果略差(部分場景有優勢 );選 ovr 時,liblinear、newton - cg、lbfgs、sag 4 種優化算法都可用 。
- MvM:以 OvO(one - vs - one )為例,T 類樣本需選兩類(T1、T2 ),T1 正例、T2 負例做二元回歸,共需 T (T - 1)/2 次分類;分類精確但速度慢;選 multinomial 時,僅 newton - cg、lbfgs、sag 優化算法可用 。
- verbose:日志冗長度,int 型,默認 0(不輸出訓練過程 );1 偶爾輸出結果,>1 則每個子模型都輸出 。
- warm_start:熱啟動參數,bool 型,默認 False ;為 True 時,下次訓練以追加樹形式(用上一次調用初始化 )。
- n_jobs:并行數,int 型,默認 1(用 CPU 1 個內核 );2 則用 2 個內核,-1 用所有 CPU 內核 。
多分類策略與算法關聯補充
OvR 相對簡單但效果略差(部分樣本分布場景有優勢 ),MvM 分類精確但速度慢;選 ovr 時,4 種優化算法(liblinear、newton - cg、lbfgs、sag )均可搭配;選 multinomial 時,僅 newton - cg、lbfgs、sag 可用 。
二·代碼
import numpy as np
# numpy是專門用于處理矩陣數據# 讀取數據集
data = np.loadtxt('datingTestSet2.txt')# 數據預處理(按需啟用,若不需要篩選可注釋)
# data_1 = data[data[:, -1] == 1] # 找出類別為1的數據
# data_2 = data[data[:, -1] == 2] # 找出類別為2的數據
# data_3 = data[data[:, -1] == 3] # 找出類別為3的數據
# data_new = np.concatenate((data_1, data_2), axis=0) # 拼接類別1和2的數據
# X = data_new[:, :-1] # 獲取特征(不含最后一列標簽)
# y = data_new[:, -1] # 獲取標簽(最后一列)# 若無需篩選類別,直接用全部數據做特征和標簽拆分
X = data[:, :-1] # 獲取所有數據的特征(不含最后一列標簽)
y = data[:, -1] # 獲取所有數據的標簽(最后一列)"""建立模型"""
from sklearn.model_selection import train_test_split
# 專門用來對數據集進行切分的函數# 拆分數據集為訓練集和測試集
x_train_w, x_test_w, y_train_w, y_test_w = train_test_split(X, y, test_size=0.3, random_state=1000
)from sklearn.linear_model import LogisticRegression
# 邏輯回歸的類,所有的算法都封裝再這個類# 創建邏輯回歸模型實例
lr = LogisticRegression(C=0.01)
# 訓練模型(用訓練集特征和標簽)
lr.fit(x_train_w, y_train_w)# 測試集預測
test_predicted = lr.predict(x_test_w)
# 計算模型在測試集上的準確率
result = lr.score(x_test_w, y_test_w)
print("模型在測試集上的準確率:", result)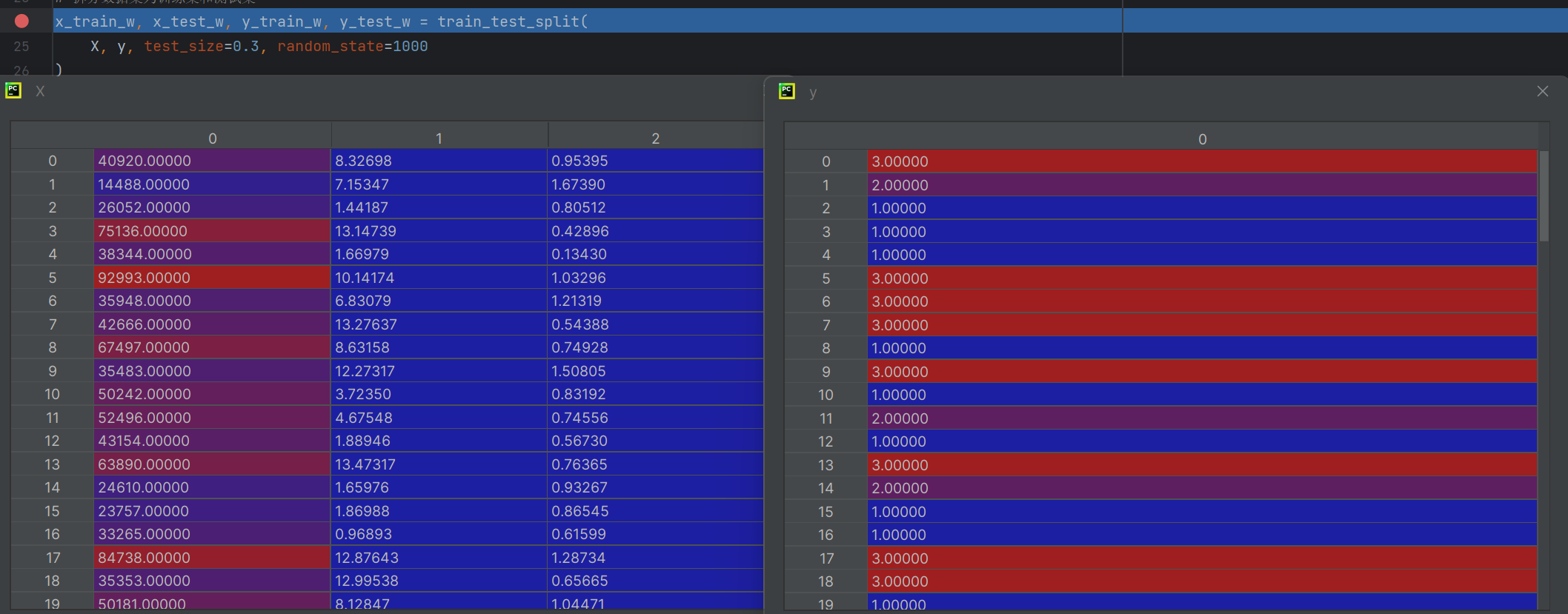
抽取30%測試集剩下的70%是訓練集
x_train_w, x_test_w, y_train_w, y_test_w = train_test_split?訓練級的 x。測試機 x 訓練機的 y,測試機的 y

lr中的coef
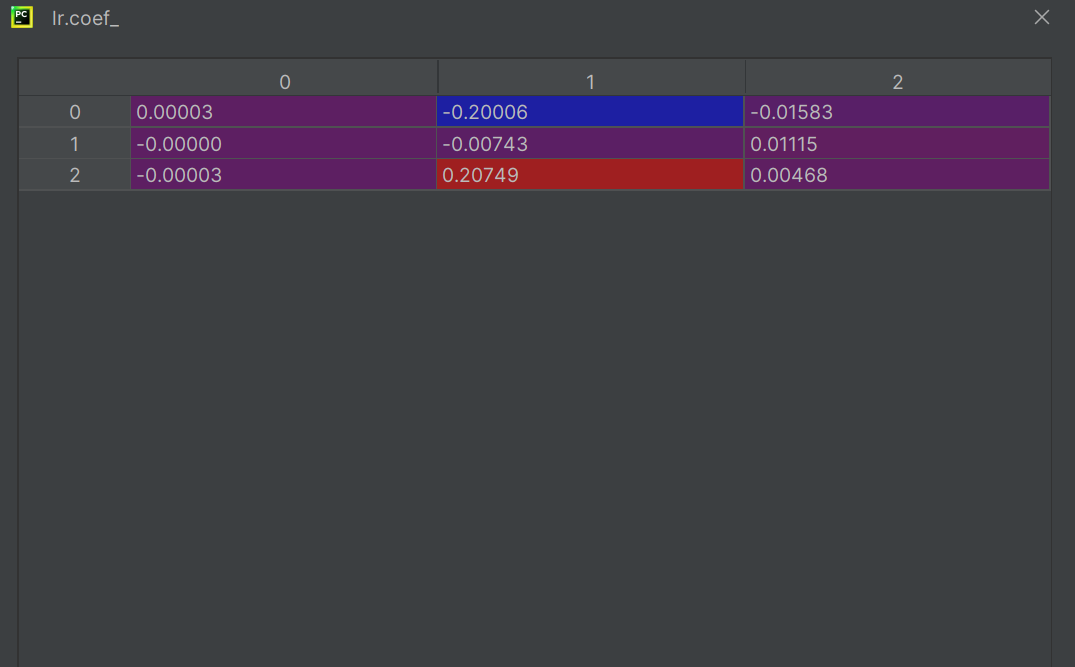
建立三條數據線,三條方程
三·關于銀行的案例下篇文章會講
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
from pylab import mpl
from sklearn import metricsdata = pd.read_csv(r"./creditcard.csv")scaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data[['Amount']])
data = data.drop(['Time'], axis=1)X_whole = data.drop('Class', axis=1)
y_whole = data['Class']
x_train_w, x_test_w, y_train_w, y_test_w = train_test_split(X_whole, y_whole, test_size=0.3, random_state=1000
)lr = LogisticRegression(C=0.01)
lr.fit(x_train_w, y_train_w)
test_predicted = lr.predict(x_test_w)
result = lr.score(x_test_w, y_test_w)print(metrics.classification_report(y_test_w, test_predicted))mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']
mpl.rcParams['axes.unicode_minus'] = False
labels_count = pd.value_counts(data['Class'])
labels_count.plot(kind='bar')
plt.title("正負例樣本數")
plt.xlabel("類別")
plt.ylabel("頻數")
plt.show()第7講:VS實用調試技巧)














-組件)



