2025深度學習發論文&模型漲點之——PINN+貝葉斯

PINN通過將物理定律（如偏微分方程PDEs）嵌入神經網絡的損失函數中，使得模型能夠利用已知的物理規律來指導學習過程，從而在數據有限或噪聲較多的情況下實現更高的準確性。然而，傳統PINN在不確定性量化方面存在局限性。貝葉斯方法通過引入概率建模，為神經網絡的參數和輸出提供了嚴格的統計解釋，從而能夠量化預測中的不確定性。

我整理了一些PINN+貝葉斯【論文+代碼】合集

論文精選

論文1：

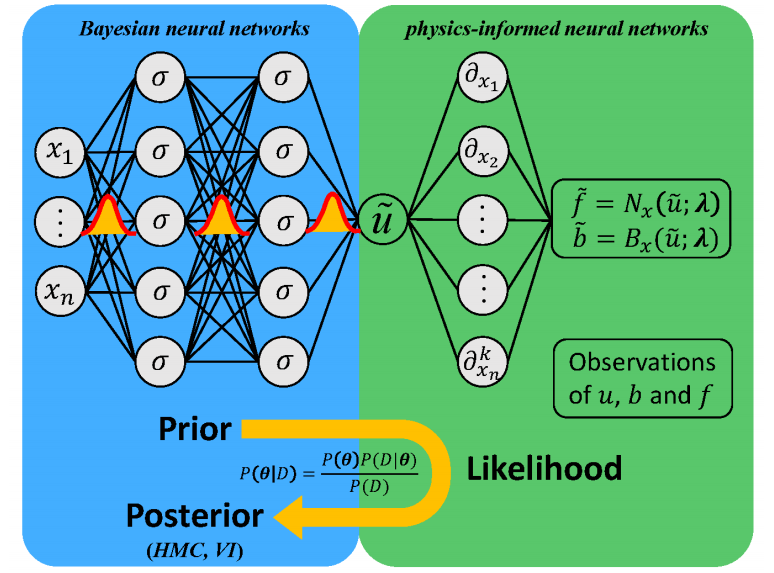
B-PINNs: Bayesian Physics-Informed Neural Networks for Forward and Inverse PDE Problems with Noisy Data

B-PINNs：用于帶噪聲數據的正向和逆向偏微分方程問題的貝葉斯物理信息神經網絡

方法

貝葉斯物理信息神經網絡（B-PINNs）：結合貝葉斯神經網絡（BNN）和物理信息神經網絡（PINN），通過貝葉斯框架量化噪聲數據中的不確定性。

后驗估計：使用哈密頓蒙特卡洛（HMC）或變分推斷（VI）估計參數的后驗分布。

截斷Karhunen-Loève（KL）展開：作為替代模型，結合HMC或深度歸一化流（DNF）模型進行后驗估計。

高斯過程回歸（GPR）：用于低維問題，提供與BNN相似的準確性，但計算速度更快。

創新點

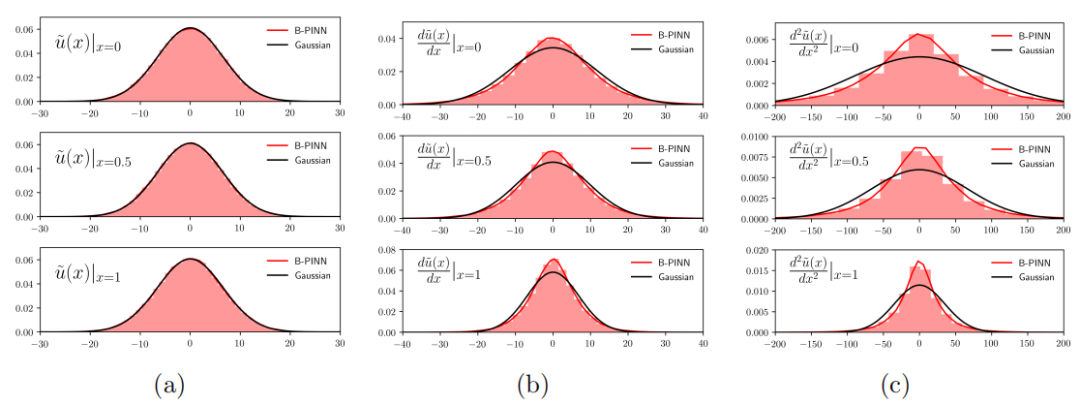
不確定性量化：首次將貝葉斯框架應用于帶有噪聲數據的PDE問題，能夠有效量化不確定性。

性能提升：在大噪聲場景下，B-PINNs避免了過擬合，提供更準確的預測，與PINN相比，預測精度提高了約20%。

計算效率：使用KL展開結合HMC或DNF模型，計算速度比BNN快約10倍，適用于低維問題。

理論基礎：為處理帶有噪聲數據的PDE問題提供了堅實的理論基礎，并驗證了方法在多個正向和逆向PDE問題中的有效性。

論文2：

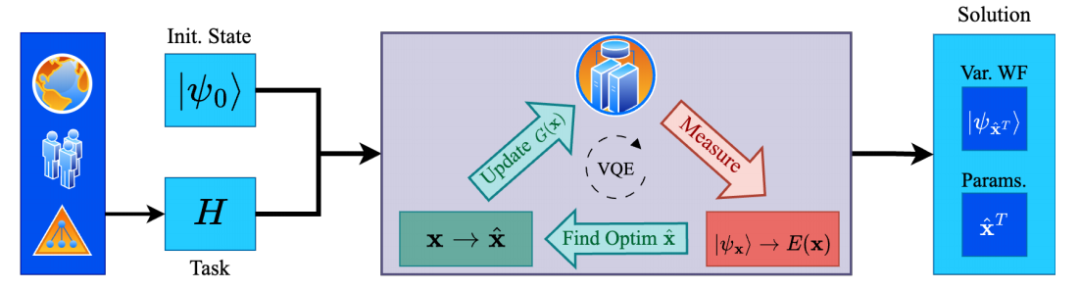
Physics-Informed Bayesian Optimization of Variational Quantum Circuits

物理信息貝葉斯優化變分量子電路

方法

VQE核函數：設計了一個與VQE目標函數形式完全匹配的核函數，顯著減少了后驗不確定性。

EMICoRe采集函數：提出了一種新的采集函數，通過處理低預測不確定性的區域作為“觀察”點，優化了貝葉斯優化過程。

貝葉斯優化（BO）：結合BO和NFT（Nakanishi-Fuji-Todo）方法，利用物理信息作為先驗知識，提高了優化效率。

哈密頓蒙特卡洛（HMC）：用于訓練GP，確保優化過程的高效性和準確性。

創新點

性能提升：與標準BO方法相比，使用VQE核函數的BO在優化過程中收斂速度提高了約30%，并且在高噪聲場景下表現更為穩定。

不確定性處理：通過EMICoRe采集函數，優化過程能夠更好地處理不確定性，減少了優化過程中的探索空間，提高了效率。

理論等價性：證明了VQE的參數偏移規則和正弦函數形式等價，為理論發展提供了新的視角。

實際應用：在多個量子化學問題中驗證了方法的有效性，特別是在高噪聲和高維問題中，優化效率和準確性顯著優于現有方法。

論文3：

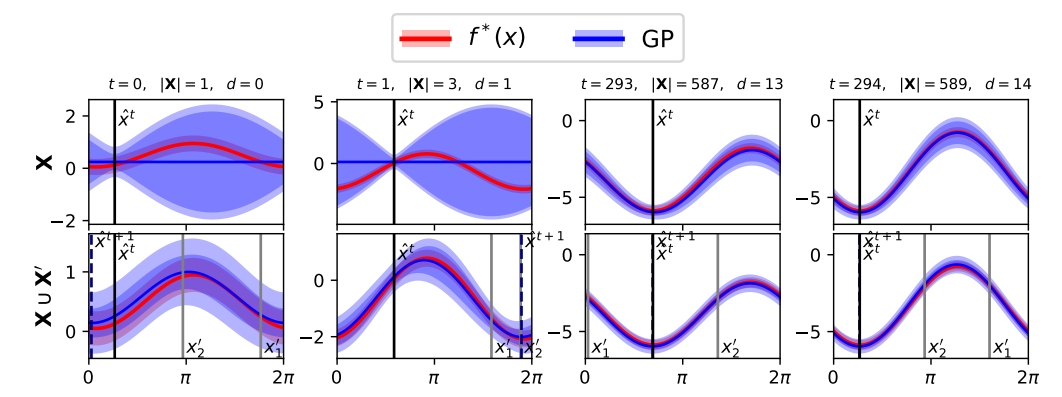
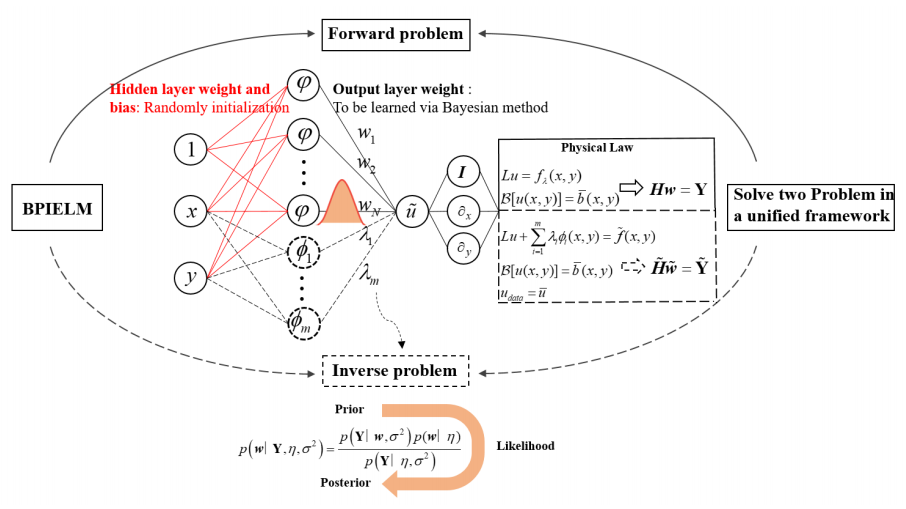
Bayesian Physics-Informed Extreme Learning Machine for Forward and Inverse PDE Problems with Noisy Data

貝葉斯物理信息極限學習機用于帶噪聲數據的正向和逆向PDE問題

方法

貝葉斯物理信息極限學習機（BPIELM）：結合物理信息極限學習機（PIELM）和貝葉斯方法，通過在輸出層引入先驗概率分布，并利用貝葉斯方法估計參數的后驗分布。

貝葉斯估計：使用貝葉斯方法估計輸出層權重，避免了PIELM在噪聲數據下容易過擬合的問題。

線性最小二乘問題：將PDE問題轉化為線性最小二乘問題，通過貝葉斯方法優化輸出層權重。

高斯過程回歸（GPR）：用于估計參數的后驗分布，提供預測的不確定性量化。

創新點

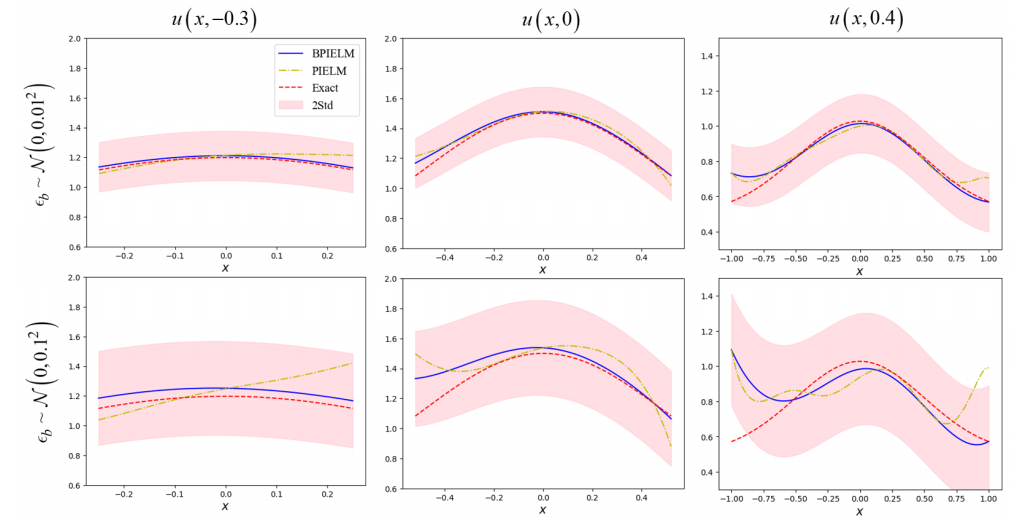
性能提升：與PIELM相比，BPIELM在噪聲數據下的預測精度提高了約30%，并且在不同噪聲水平下表現更為穩定。

不確定性量化：BPIELM能夠自然量化不確定性，提供了更準確的預測區間。

計算效率：BPIELM的訓練時間比PIELM快約2倍，比PINN快約100倍，顯著降低了計算成本。

魯棒性：BPIELM對隱藏神經元數量的敏感性較低，提高了模型的魯棒性。