零基礎-動手學深度學習-8.3. 語言模型和數據集

很至關重要的一章:

8.3.1.?學習語言模型

8.3.2.?馬爾可夫模型與n元語法?

n元語法看的序列長度是固定的，?存儲的序列長是有限且可控的，使用統計方法的時候通常使用這個模型！！！統計方法！！！

8.3.3.?自然語言統計?

?我們看看在真實數據上如果進行自然語言統計。根據?8.2節中介紹的時光機器數據集構建詞表，并打印前10個最常用的（頻率最高的）單詞。

import random
import torch
from d2l import torch as d2ltokens = d2l.tokenize(d2l.read_time_machine())
# 因為每個文本行不一定是一個句子或一個段落，因此我們把所有文本行拼接到一起
corpus = [token for line in tokens for token in line]
vocab = d2l.Vocab(corpus)
vocab.token_freqs[:10]輸出：
[('the', 2261),('i', 1267),('and', 1245),('of', 1155),('a', 816),('to', 695),('was', 552),('in', 541),('that', 443),('my', 440)]

在自然語言處理（NLP）、文本分析和機器學習領域，"corpus"（語料庫）是指一個大規模的文本集合。

正如我們所看到的，最流行的詞看起來很無聊，這些詞通常被稱為停用詞（stop words），因此可以被過濾掉。盡管如此，它們本身仍然是有意義的，我們仍然會在模型中使用它們。此外，還有個明顯的問題是詞頻衰減的速度相當地快。例如，最常用單詞的詞頻對比，第10個還不到第1個的1/5。為了更好地理解，我們可以畫出的詞頻圖：

freqs = [freq for token, freq in vocab.token_freqs]
d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)',xscale='log', yscale='log')
#token是已經排過序的，而且這里的token還用了log處理，代表的是80%出現都是20%的詞，因為這里log是線性關系。

?建模的意義在于說明單純平滑化的的不合理性：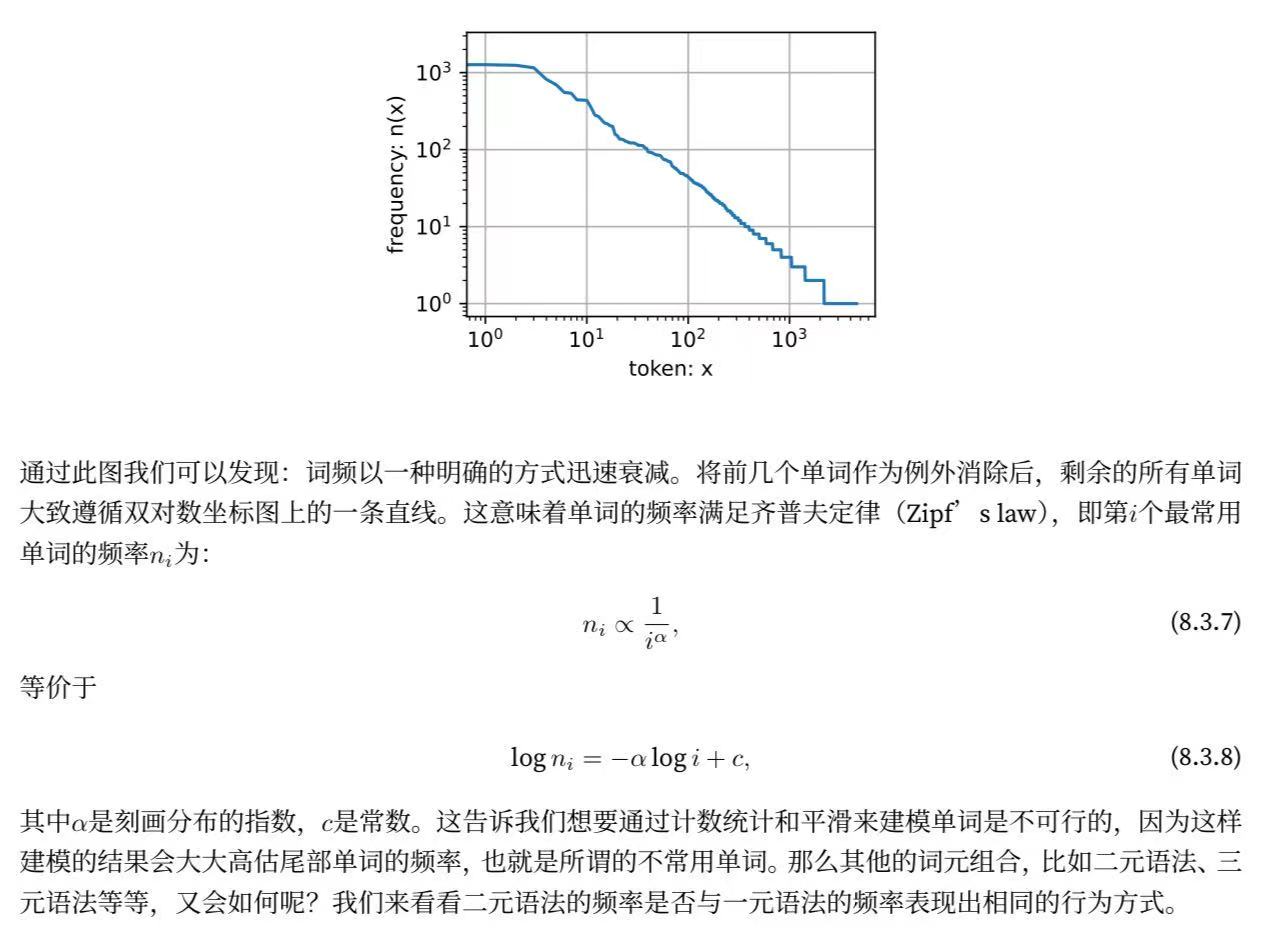

bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
#這里是直接打包成一個zip，corpus[:-1]是把最后一個拿掉，corpus[1:]是從1才開始，每一次拿到就是元素和元素后面一個
bigram_vocab = d2l.Vocab(bigram_tokens)
bigram_vocab.token_freqs[:10]輸出：
[(('of', 'the'), 309),(('in', 'the'), 169),(('i', 'had'), 130),(('i', 'was'), 112),(('and', 'the'), 109),(('the', 'time'), 102),(('it', 'was'), 99),(('to', 'the'), 85),(('as', 'i'), 78),(('of', 'a'), 73)]

?這里值得注意：在十個最頻繁的詞對中，有九個是由兩個停用詞組成的，只有一個與“the time”有關。我們再進一步看看三元語法的頻率是否表現出相同的行為方式。

這里稍微提一下這個負數在list中的使用，一般表示的就是倒數，：-2就是一直到倒數第二個元素。

trigram_tokens = [triple for triple in zip(corpus[:-2], corpus[1:-1], corpus[2:])]
#這里就是三元了
trigram_vocab = d2l.Vocab(trigram_tokens)
trigram_vocab.token_freqs[:10]輸出：
[(('the', 'time', 'traveller'), 59),(('the', 'time', 'machine'), 30),(('the', 'medical', 'man'), 24),(('it', 'seemed', 'to'), 16),(('it', 'was', 'a'), 15),(('here', 'and', 'there'), 15),(('seemed', 'to', 'me'), 14),(('i', 'did', 'not'), 14),(('i', 'saw', 'the'), 13),(('i', 'began', 'to'), 13)]

?最后，我們直觀地對比三種模型中的詞元頻率：一元語法、二元語法和三元語法。

bigram_freqs = [freq for token, freq in bigram_vocab.token_freqs]
trigram_freqs = [freq for token, freq in trigram_vocab.token_freqs]
d2l.plot([freqs, bigram_freqs, trigram_freqs], xlabel='token: x',ylabel='frequency: n(x)', xscale='log', yscale='log',legend=['unigram', 'bigram', 'trigram'])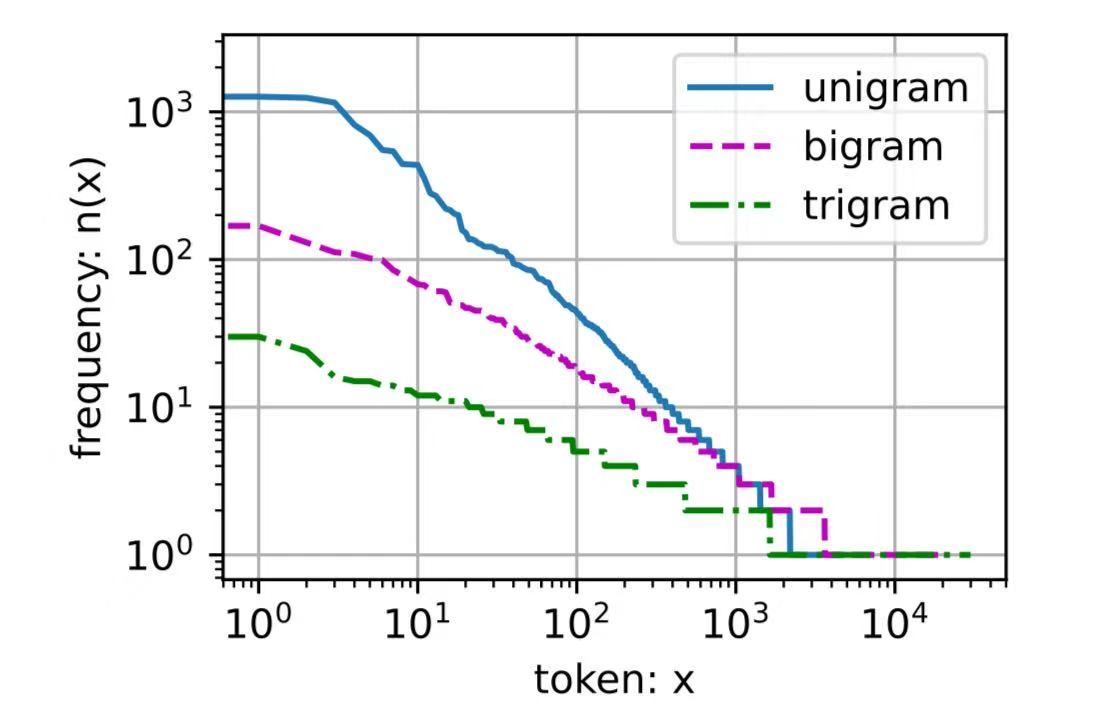

這張圖非常令人振奮！原因有很多：

除了一元語法詞，單詞序列似乎也遵循齊普夫定律， 盡管公式?(8.3.7)中的指數更小（指數的大小受序列長度的影響）；
詞表中元組的數量并沒有那么大，這說明語言中存在相當多的結構，這些結構給了我們應用模型的希望；
很多元組很少出現，這使得拉普拉斯平滑非常不適合語言建模。作為代替，我們將使用基于深度學習的模型。

?8.3.4.?讀取長序列數據

?8.3.4.1.?隨機采樣

在隨機采樣中，每個樣本都是在原始的長序列上任意捕獲的子序列。在迭代過程中，來自兩個相鄰的、隨機的、小批量中的子序列不一定在原始序列上相鄰。對于語言建模，目標是基于到目前為止我們看到的詞元來預測下一個詞元， 因此標簽是移位了一個詞元的原始序列。

下面的代碼每次可以從數據中隨機生成一個小批量。在這里，參數batch_size指定了每個小批量中子序列樣本的數目，參數num_steps是每個子序列中預定義的時間步數。

為了解決原本太多冗余的序列對的問題，深度學習的分割又有可能覆蓋不了所有序列對，因此核心思想在于隨機起始去取T長的序列，下面這個代碼挺刁的，可以看看寫的非常簡潔。

def seq_data_iter_random(corpus, batch_size, num_steps):  #@save ns類似于tao 每次取多長"""使用隨機抽樣生成一個小批量子序列"""# 從隨機偏移量開始對序列進行分區，隨機范圍包括num_steps-1corpus = corpus[random.randint(0, num_steps - 1):]# 減去1，是因為我們需要考慮標簽是后一位# random.randint(a, b)：生成一個在 a 和 b 之間（包括 a 和 b）的隨機整數。num_subseqs = (len(corpus) - 1) // num_steps# 長度為num_steps的子序列的起始索引initial_indices = list(range(0, num_subseqs * num_steps, num_steps))# 在隨機抽樣的迭代過程中，# 來自兩個相鄰的、隨機的、小批量中的子序列不一定在原始序列上相鄰random.shuffle(initial_indices)#shuffle一下保證每次取的序列是隨機的def data(pos):# 返回從pos位置開始的長度為num_steps的序列return corpus[pos: pos + num_steps]num_batches = num_subseqs // batch_size #計算有多少次batchfor i in range(0, batch_size * num_batches, batch_size):# 在這里，initial_indices包含子序列的隨機起始索引 為了每次能把一個batch拿出來initial_indices_per_batch = initial_indices[i: i + batch_size]X = [data(j) for j in initial_indices_per_batch]Y = [data(j + 1) for j in initial_indices_per_batch]yield torch.tensor(X), torch.tensor(Y)

下面我們生成一個從0到34的序列。假設批量大小為2，時間步數為5，這意味著可以生成35-1/5=6個“特征－標簽”子序列對。如果設置小批量大小為2，我們只能得到3個小批量。

my_seq = list(range(35))
for X, Y in seq_data_iter_random(my_seq, batch_size=2, num_steps=5):print('X: ', X, '\nY:', Y)輸出：
X:  tensor([[13, 14, 15, 16, 17],[28, 29, 30, 31, 32]])
Y: tensor([[14, 15, 16, 17, 18],[29, 30, 31, 32, 33]])
X:  tensor([[ 3,  4,  5,  6,  7],[18, 19, 20, 21, 22]])
Y: tensor([[ 4,  5,  6,  7,  8],[19, 20, 21, 22, 23]])
X:  tensor([[ 8,  9, 10, 11, 12],[23, 24, 25, 26, 27]])
Y: tensor([[ 9, 10, 11, 12, 13],[24, 25, 26, 27, 28]])

?8.3.4.2.?順序分區

在迭代過程中，除了對原始序列可以隨機抽樣外，我們還可以保證兩個相鄰的小批量中的子序列在原始序列上也是相鄰的。這種策略在基于小批量的迭代過程中保留了拆分的子序列的順序，因此稱為順序分區。?

def seq_data_iter_sequential(corpus, batch_size, num_steps):  #@save"""使用順序分區生成一個小批量子序列"""# 從隨機偏移量開始劃分序列offset = random.randint(0, num_steps)num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_sizeXs = torch.tensor(corpus[offset: offset + num_tokens])Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)num_batches = Xs.shape[1] // num_stepsfor i in range(0, num_steps * num_batches, num_steps):X = Xs[:, i: i + num_steps]Y = Ys[:, i: i + num_steps]yield X, Y

基于相同的設置，通過順序分區讀取每個小批量的子序列的特征X和標簽Y。通過將它們打印出來可以發現：迭代期間來自兩個相鄰的小批量中的子序列在原始序列中確實是相鄰的。

for X, Y in seq_data_iter_sequential(my_seq, batch_size=2, num_steps=5):print('X: ', X, '\nY:', Y)輸出：
X:  tensor([[ 0,  1,  2,  3,  4],[17, 18, 19, 20, 21]])
Y: tensor([[ 1,  2,  3,  4,  5],[18, 19, 20, 21, 22]])
X:  tensor([[ 5,  6,  7,  8,  9],[22, 23, 24, 25, 26]])
Y: tensor([[ 6,  7,  8,  9, 10],[23, 24, 25, 26, 27]])
X:  tensor([[10, 11, 12, 13, 14],[27, 28, 29, 30, 31]])
Y: tensor([[11, 12, 13, 14, 15],[28, 29, 30, 31, 32]])

?現在，我們將上面的兩個采樣函數包裝到一個類中，以便稍后可以將其用作數據迭代器。

class SeqDataLoader:  #@save"""加載序列數據的迭代器"""def __init__(self, batch_size, num_steps, use_random_iter, max_tokens):if use_random_iter:self.data_iter_fn = d2l.seq_data_iter_randomelse:self.data_iter_fn = d2l.seq_data_iter_sequentialself.corpus, self.vocab = d2l.load_corpus_time_machine(max_tokens)self.batch_size, self.num_steps = batch_size, num_stepsdef __iter__(self):return self.data_iter_fn(self.corpus, self.batch_size, self.num_steps)

?最后，我們定義了一個函數load_data_time_machine，它同時返回數據迭代器和詞表，因此可以與其他帶有load_data前綴的函數（如?3.5節中定義的?d2l.load_data_fashion_mnist）類似地使用。

def load_data_time_machine(batch_size, num_steps,  #@saveuse_random_iter=False, max_tokens=10000):"""返回時光機器數據集的迭代器和詞表"""data_iter = SeqDataLoader(batch_size, num_steps, use_random_iter, max_tokens)return data_iter, data_iter.vocab