一、什么是中心極限定理？

中心極限定理(Central Limit Theorem, CLT)是概率論與統計學中最重要的定理之一，它揭示了為什么正態分布在自然界和統計學中如此普遍。

?定理表述?：

設X?, X?, ..., X? 是一組獨立同分布的隨機變量序列，它們具有相同的期望值μ和有限的方差σ2。

令樣本均值：

則隨著樣本量n趨向于無窮大，樣本均值的標準化形式（啥意思？后面有解釋）：

依分布收斂于標準正態分布N(0,1)，即：

?關鍵要點?：

1. 無論原始分布如何(可以是均勻分布、指數分布、二項分布等)，樣本均值的分布都會趨近正態分布
2. 樣本量n越大，近似程度越好
3. 標準化過程：(X?-μ)/(σ/√n) ~ N(0,1)
4. 實際應用中，n>30通常被認為是"足夠大"的樣本量

二、班級學生身高分析案例

1、案例背景

假設某城市所有10歲學生的平均身高為140cm，標準差為8cm。我們隨機抽取36名學生，計算他們的平均身高。那么：

1. 這個樣本平均身高的期望值是多少？
2. 樣本平均身高的標準差是多少？
3. 樣本平均身高在138-142cm之間的概率是多少？

“標準差為8cm”和“樣本平均身高的標準差”啥關系？后面解釋

---

2、分步計算過程

?步驟1：確定參數?

• 總體均值(μ) = 140cm
• 總體標準差(σ) = 8cm
• 樣本量(n) = 36

?步驟2：計算樣本均值的期望和標準差?
根據中心極限定理：

• 樣本均值的期望 = 總體均值 = 140cm
• 樣本均值的標準差(標準誤差) = σ/√n = 8/√36 = 8/6 ≈ 1.333cm

?步驟3：標準化區間?
計算138-142cm對應的Z分數：

• 對于138cm：Z = (138-140)/1.333 ≈ -1.5
• 對于142cm：Z = (142-140)/1.333 ≈ +1.5

?步驟4：查標準正態分布表?
P(-1.5 < Z < 1.5) = P(Z < 1.5) - P(Z < -1.5) ≈ 0.9332 - 0.0668 = 0.8664

?結論?：樣本平均身高在138-142cm之間的概率約為86.64%。

---

3、可視化理解

想象你是一位老師，每年測量36名學生的平均身高。如果你重復這個過程1000次，這些平均身高的分布會形成一個鐘形曲線(正態分布)，中心在140cm，大多數(約86.64%)的結果會落在138-142cm之間。

---

三、生活中的中心極限定理

案例1：餐廳等待時間

一家快餐店單個顧客的服務時間呈右偏分布(大多數顧客很快，少數需要較長時間)。但如果你觀察100位顧客的平均服務時間，這個平均時間的分布會接近正態分布。

?為什么？??

• 單個服務時間：偏態分布
• 平均服務時間(樣本量足夠大)：正態分布
• 這使得餐廳可以更準確地預測高峰時段的平均等待時間

---

案例2：產品質量控制

工廠生產螺絲釘的長度有微小隨機差異。質檢部門不檢查每個螺絲釘，而是每天隨機抽取50個測量平均長度。

?應用CLT?：

• 即使單個螺絲釘長度不是正態分布，平均長度近似正態
• 可以設置合理的控制界限(如±3個標準差)
• 超出界限則可能意味著生產線出現問題

---

四、常見誤區

1. ?誤區一?：認為原始數據必須正態分布

   • 實際上，CLT告訴我們無論原始分布如何，樣本均值的分布都趨近正態

2. ?誤區二?：忽視樣本量的重要性

   • 對于高度非正態的分布(如指數分布)，可能需要更大的n才能良好近似

3. ?誤區三?：混淆樣本分布和抽樣分布

   • 樣本分布是原始數據的分布
   • 抽樣分布是統計量(如樣本均值)的分布

---

五、實際應用建議

1. ?確定適當樣本量?：根據數據特性，可能需要n>30或更大
2. ?檢查近似效果?：對于小樣本或極端分布，可通過模擬驗證正態近似是否合理
3. ?注意獨立性假設?：CLT要求樣本是獨立的，在時間序列或空間數據中需謹慎
4. ?結合其他方法?：對于小樣本，考慮使用t分布或其他非參數方法

---

六、總結

中心極限定理之所以重要，是因為它讓我們能夠：

• 對未知分布的數據進行推斷
• 構建置信區間和進行假設檢驗
• 簡化復雜問題的分析
• 理解為什么正態分布在自然界中如此普遍

---

七、解釋

1、“均值的標準化形式”詳解

---

1. 標準化的本質：統一量綱

想象你在比較：北京房價（均價6萬/㎡，標準差2萬），紐約房價（均價80萬美元，標準差30萬），直接比較“6萬”和“80萬”毫無意義！標準化就是將它們轉換為無單位的統一尺度，從而可比。

---

2. 均值標準化的數學定義

對于樣本均值，其標準化形式為：

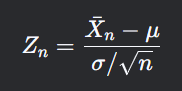
• 分子：均值與真實值的偏差（去中心化）

• 分母：均值的標準差（縮放至單位方差）

類比：假設全班考試平均分分，標準差。

• 當n=1時（單次觀測），公式簡化為Z=(X-μ)/σ

• 你的成績

• 標準化值
  →?你比平均分高1.5個標準差（無論原始分數單位是分、美元還是厘米）

---

3. 幾何直觀：拉伸與平移

• 平移（分子）：把分布曲線的中心移到0

• 縮放（分母）：調整分布寬度，使標準差變為1

---

4. 記憶口訣

“減均值，除標準差，數據變身標準分”—— 就像把不同貨幣兌換成美元后再比較！

5. 練習

假設某App日活用戶均值萬人，標準差萬。某天日活1.5萬人，其標準化值是多少？
答案：（即“高出平均值1個標準差”）

2、“標準差為8cm”和“樣本平均身高的標準差”?

想象你是一位老師，負責測量全班同學的身高。

?1. 單次測量的波動（原始標準差：標準差為8cm）??

• 每個學生的身高都不一樣，有的高，有的矮。
• ?原始標準差（σ）?? 衡量的是“單個學生身高”的波動程度。比如，σ=8cm，意味著大部分學生的身高在“平均身高±8cm”之間。

?2. 多次測量平均值的波動（標準誤差：樣本平均身高的標準差）??

現在，你不滿足于只看單個學生的身高，而是想計算全班平均身高。

• 如果你只測5個學生，算出的平均身高可能和真實平均差很多（比如碰巧抽到了幾個特別高的）。
• 如果你測50個學生，算出的平均身高會更接近真實值（因為極端值的影響被“平均”掉了）。

?樣本平均身高的標準差（標準誤差）?? 衡量的是：

??“不同樣本的平均身高”之間的波動有多大？??

計算公式：

?3. 為什么除以√n？??

• ?樣本量越大，平均值越穩定?（極端值的影響被稀釋）。
• ?√n 的數學意義：
  • 如果樣本量從 4 增加到 16（4倍），標準誤差會減半（因為 √16=4，σ/4 比 σ/2 更小）。
  • 這就是為什么“大樣本調查更可靠”！

?4. 現實例子?

假設：

• 全國10歲兒童身高的原始標準差 σ=8cm。
• 你調查了 ?100個孩子?（n=100），計算平均身高。

那么：

這意味著：

• 如果你重復抽樣100人很多次，?不同樣本的平均身高? 會在“真實平均±0.8cm”之間波動。
• 對比單次測量的波動（±8cm），平均值的波動（±0.8cm）小得多！

?5. 類比：咖啡店排隊時間?

• ?單次排隊時間?：有時5分鐘，有時30分鐘（波動大，σ=10分鐘）。
• ?平均10次排隊的等待時間?：波動會小很多（σ/√10 ≈ 3.16分鐘）。
• ?平均100次排隊的等待時間?：波動更小（σ/√100 = 1分鐘）。

?結論?：

• ?標準誤差? 告訴你，?樣本均值有多可靠。
• ?樣本量越大，均值越精準?（就像多次測量取平均會更準一樣）。

擴大樣本量可以減少誤差。