題目鏈接

LeetCode復寫零

題目描述

?

題目解析

一、問題理解

題目要求：給定一個整數數組?arr，在不創建新數組的情況下，將每個出現的?0?復寫一遍（即一個?0?變成兩個?0），同時保持其他元素的相對順序不變。復寫后超出原數組長度的元素需要舍棄。

示例：

• 輸入：[1,0,2,3,0,4,5,0]
• 輸出：[1,0,0,2,3,0,0,4]

?核心難點：

1. 必須在原數組上操作（空間復雜度 O(1)）
2. 復寫 0 會改變后續元素的位置，直接從左到右處理會覆蓋未處理的元素

?

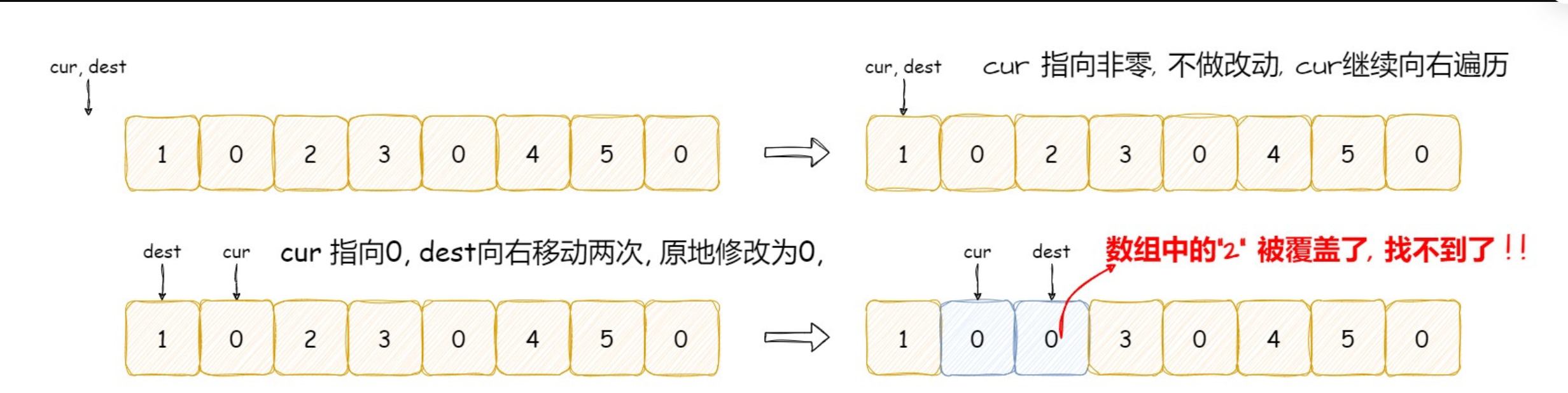二、解題思路：雙指針法

為解決上述問題，我們采用「雙指針 + 兩次遍歷」的策略：

第一次遍歷：確定最終需要保留的元素范圍（找到復寫邊界） ?

第二次遍歷：從邊界處從右向左復寫元素（避免覆蓋未處理的元素）?

?

三、分步解析代碼

以下是完整代碼，我們逐部分解析：?

?

四、關鍵步驟詳解

1. 尋找復寫邊界（第一次遍歷）

• 目的：確定原數組中哪些元素需要參與復寫（避免處理超出最終數組長度的元素）。
• 雙指針作用：
  • cur：遍歷原數組的每個元素（從左到右）。
  • dest：模擬復寫后的數組長度（每遇到?0?加?2，非?0?加?1）。
• 終止條件：當?dest >= n-1?時停止（復寫指針已超出數組范圍）。

示例過程（輸入?[1,0,2,3]，n=4）：

• 初始：cur=0，dest=-1
• cur=0（元素?1）：dest +=1 → 0，dest < 3，cur→1
• cur=1（元素?0）：dest +=2 → 2，dest < 3，cur→2
• cur=2（元素?2）：dest +=1 → 3，dest == 3（n-1），停止遍歷。
• 最終：cur=2，dest=3（復寫邊界確定）。

2. 處理邊界情況

• 特殊場景：當?dest == n?時，說明最后一個元素是?0，且復寫后會超出數組長度（例如輸入?[0,1,2]，復寫后?dest?會達到?3，等于?n=3）。
• 處理方式：
  • 最后一個?0?只能復寫?1?次（放在數組末尾?arr[n-1]）。
  • 調整指針：cur?回退?1（跳過該?0?的二次處理），dest?回退?2（指向?n-2）。

3. 從右向左復寫（第二次遍歷）

• 核心邏輯：從?cur?位置向左遍歷，將元素復寫到?dest?位置（避免覆蓋未處理的元素）。
• 復寫規則：
  • 非?0?元素：直接復制到?dest?位置，然后雙指針左移。
  • 0?元素：連續復制兩個?0?到?dest?和?dest-1?位置，然后雙指針左移。

示例過程（續上例?[1,0,2,3]）：

• 初始：cur=2，dest=3
• cur=2（元素?2）：arr[3] = 2，dest→2，cur→1
• cur=1（元素?0）：arr[2] = 0，arr[1] = 0，dest→0，cur→0
• cur=0（元素?1）：arr[0] = 1，dest→-1，cur→-1
• 最終結果：[1,0,0,2]（符合預期）。

五、復雜度分析

• 時間復雜度：O(n)，兩次遍歷數組，總操作次數與數組長度成正比。
• 空間復雜度：O(1)，僅使用常數個額外變量，在原數組上操作。

通過這種雙指針策略，我們高效地解決了復寫零的問題，既保證了原地操作，又避免了元素覆蓋的問題。關鍵在于先確定復寫邊界，再從后往前處理，這是解決類似「原地修改數組」問題的常用技巧。