1. 決策樹與熵

1.1 決策樹簡介

• 下面有一個貸申請樣本表，有許多特征
  
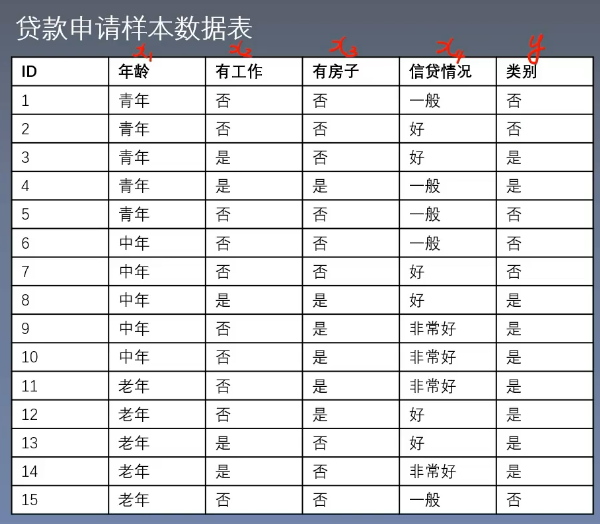
• 我們根據特征數據生成一棵樹，比如年齡有青年，中年，老年三個類別，那么就有三個分支，分別對應著三種類別。如果是青年那么就看工作，如果有工作就給他貸款，如果沒工作就不給他貸款。以上面這個例子來理解這棵樹
  
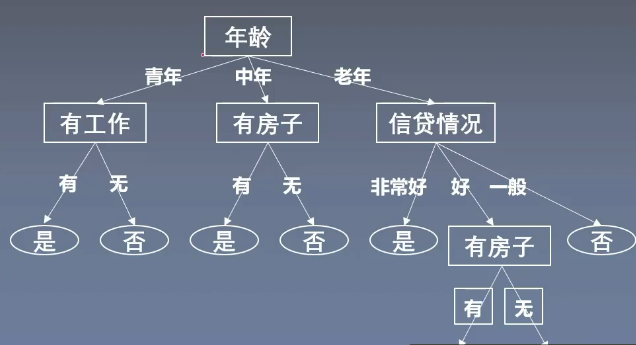
• 再舉一個例子：我們有一個樣本：老年，有工作，沒房子，信貸情況好，那么我們就可以走這樣的一條路
  
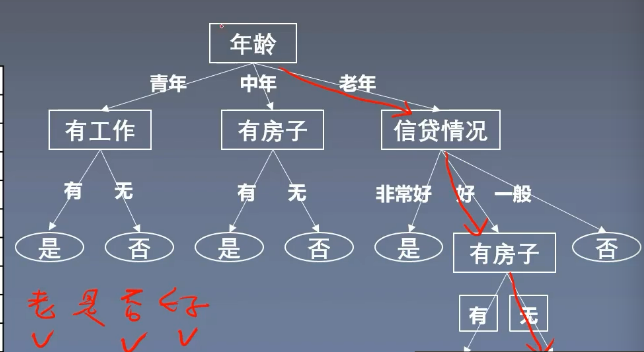
• 為什么先給年齡而不是先給工作呢？換句話說是怎么選擇特征構建樹的呢？
  • 這不是我們人為決定的，而是要進行計算

1.2 熵

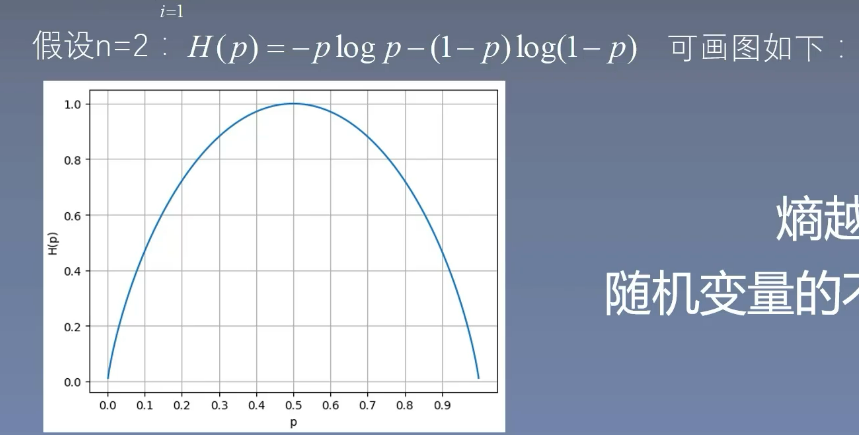
• 熵表示不確定性，定義如下：其中 $n$ 為特征數，$p_i$ 表示一個概率
  
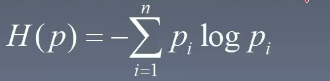
• 假設 $n=2$，則有：圖中越靠近 $p=0.5$（即越不確定），熵就越大。這表明熵越大，隨機變量的不確定性就越大
  

1.3 熵的計算舉例

• 例：我們需要計算我們數據集的熵，計算數據集的熵要算的是目標變量（或叫做類別標簽），在這里我們是計算是否給這個人貸款，即最后一列
  
• 我們把 $D$ 稱作我們的一個數據集，$|D|$ 表示數據集的條數，在這個例子為 $|D|=15$
• $k$ 表示目標變量的種類數，在這個例子為 $k=2$
• $C_k$ 表示當前的這個類別條數有多個條，比如否有 6 條，那么 $C_1=6$
• 最后用下面的這個公式算出來即可
  

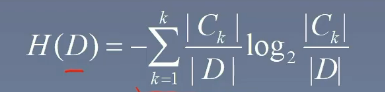
2. 條件熵

2.1 條件熵介紹

• 還是上節課的這個貸款數據集
  
• 條件熵的公式為含義為：在給定 X 為多少的條件下，計算 Y 的熵是多少
• 由于 X 有很多個取值，我們對它展開。比如之類年齡有青年，中年，老年
• 這里 $p_i$ 是變量 X 取值為 $x_i$ 的概率
  
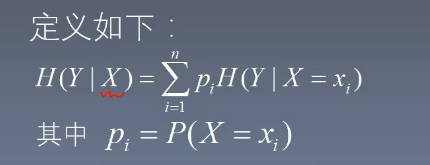
• 那么回到數據集的條件熵的計算公式來說，下面公式的含義如下：
  • 這里的 $A$ 為條件變量，比如年齡
  • $D$ 為數據集，$|D|$ 為數據集條數，$|D_i|$ 為條件變量當前取值的條數
  • $n$ 為條件的種類數
  • $K$ 依舊為目標變量的種類數
  • $|D_{ik}|$ 為兩個變量同時滿足的條數
    

2.2 條件熵的計算例子

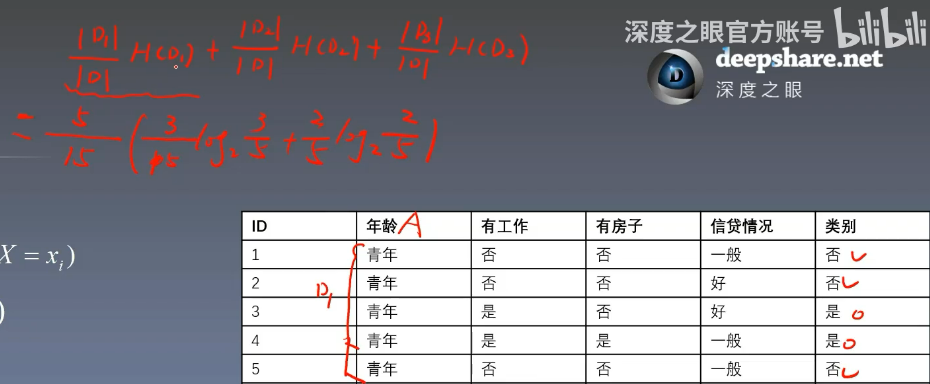
• 我們以年齡為條件變量來嘗試計算以它為條件的條件熵
• 以年齡為青年時為例子，我們 $i=1$ 為青年，這里的 $\frac{|D|}{|D_1|}=\frac{5}{15}$，總共有 $5$ 個青年，然后右部的連加就是在以青年為條件下的目標變量的信息熵，所以有式子的右半部分的展開
• 對年齡的三個類別都做一次這樣的操作后求連加即為以青年為條件的條件熵
  

3. 信息增益與 ID3 算法

3.1 信息增益

• 信息增益（也叫互信息）的定義如下：我們用符號 $g(D,A)$ 來表示，即用數據集的信息熵減去以某個特征為條件的條件熵
  
• 根據信息增益準則的特征選擇方法：
  1. 對訓練數據集（或子集）D，計算其每個特征的信息增益
  2. 比較它們的大小，選擇信息增益最大的特征
• 信息增益算法：

  1. 計算數據集 D 的信息熵 H(D)：
     

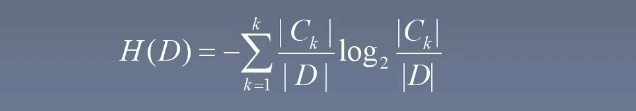
  2. 計算特征 A 對數據集 D 的經驗條件熵 H(D|A)
     

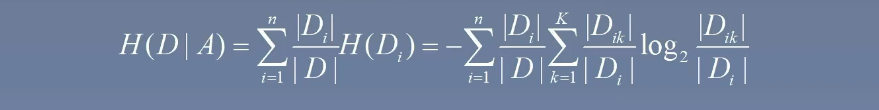
  3. 計算信息增益
     

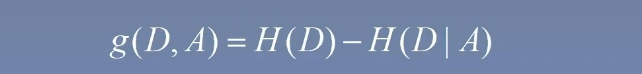
• 例子：
  
  

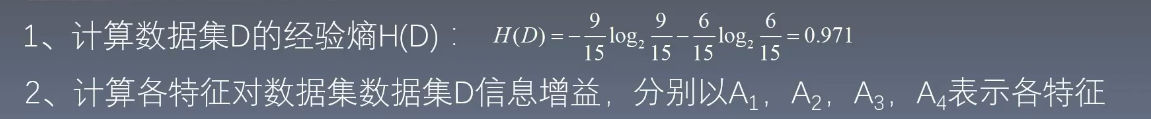
3.2 ID3 算法構建決策樹

• ID3 算法：在決策樹遞歸構建過程中，使用信息增益的方法進行特征選擇

• 決策樹生成過程：

  1. 從根節點開始計算所有特征的信息增益，選擇信息增益最大的特征作為結點特征
  2. 再對子節點遞歸調用以上方法，構建決策樹
  3. 所有特征信息增益很小或沒有特征可以選擇時遞歸結束得到一顆決策樹

• 比如說我們開始選擇了 $A_3$ 作為我們的根節點（根據上面的計算得到），此時我們會往下分叉出是或者否，然后我們又根據是或者否的子集來遞歸計算信息增益，比如是對應一個子集，否又對應一個子集