10 門控激活函數
10.1 GLU:門控線性單元函數Gated Linear Unit
10.2 GTU:門控Tanh單元函數Gated Tanh Unit
自門控激活函數(Self-gated activation function)
是一種通過自身機制動態調節信息流動的激活函數,其核心在于模型能夠根據輸入數據自身的特征自動調整信息傳遞的強度,無需外部控制信號。 ?
核心特點
- ?動態調節?:根據輸入數據的內在屬性(如數值大小、梯度變化等)自動開啟或關閉信息傳遞,增強模型對復雜數據的處理能力。 ?
- 非線性特性?:通過非線性變換實現更復雜的特征提取,提升模型表達能力。 ?
- 可微性?:所有點均可微,便于訓練過程中優化參數。 ?
- 典型應用
在深度學習模型中(如Transformer、FFN層),自門控激活函數通過動態調整信息流動,優化長序列處理和復雜語義關系的建模能力。 ?
- 與傳統激活函數的區別
傳統激活函數(如ReLU)僅對輸入信號進行固定閾值處理,而自門控激活函數通過內部機制實現更精細的信息篩選,尤其在處理小數值輸入時能起到正則化效果。
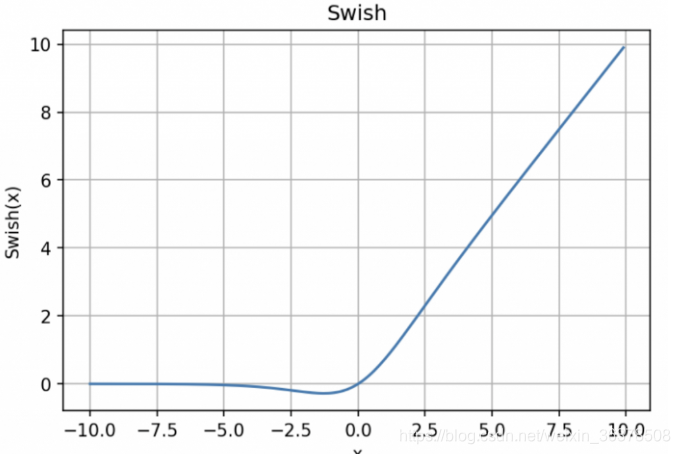
10.3 Swish:自門控激活函數
y = x * sigmoid (x)
Swish 的設計受到了 LSTM 和高速網絡中 gating 的 sigmoid函數使用的啟發。我們使用相同的 gating 值來簡化 gating 機制,這稱為 self-gating。
self-gating的優點在于它只需要簡單的標量輸入,而普通的 gating 則需要多個標量輸入。這使得諸如 Swish 之類的 self-gated激活函數能夠輕松替換以單個標量為輸入的激活函數(例如 ReLU),而無需更改隱藏容量或參數數量。Swish 激活函數的主要優點如下:
「無界性」有助于防止慢速訓練期間,梯度逐漸接近 0并導致飽和;(同時,有界性也是有優勢的,因為有界激活函數可以具有很強的正則化,并且較大的負輸入問題也能解決);
導數恒 > 0;
平滑度在優化和泛化中起了重要作用。
Swish在原點附近不是飽和的,只有負半軸遠離原點區域才是飽和的,而ReLu在原點附近也有一半的空間是飽和的。而我們在訓練模型時,一般采用的初始化參數是均勻初始化或者正態分布初始化,不管是哪種初始化,其均值一般都是0,也就是說,初始化的參數有一半處于ReLu的飽和區域,這使得剛開始時就有一半的參數沒有利用上。特別是由于諸如BN之類的策略,輸出都自動近似滿足均值為0的正態分布,因此這些情況都有一半的參數位于ReLu的飽和區。相比之下,Swish好一點,因為它在負半軸也有一定的不飽和區,所以參數的利用率更大。[FROM 蘇劍林 https://kexue.fm/archives/4647]
10.3.1 hswish
激活函數 h-swish是MobileNetV3相較于V2的一個創新,是在谷歌大腦2017年的論文Searching for Activation Functions中swish數的基礎上改進而來,用于替換V2中的部分ReLU6。
優點: 與 swish相比 hard swish減少了計算量,具有和 swish同樣的性質。
缺點: 與 relu6相比 hard swish的計算量仍然較大。
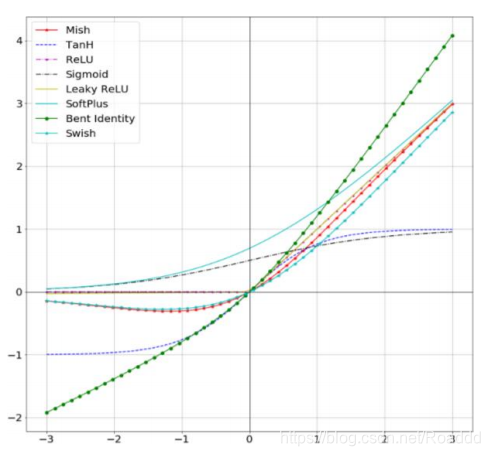
10.4 Mish:自門控激活函數
里面是softplus
Mish優點:
- 和Swish一樣
- 比 ReLU慢
- Cannot 100% guarantee
- Could pair with Ranger Optimizer(2019,Hinton)
- 比Swish穩定。
- 補充:
1.無上界有下界:無上界是任何激活函數都需要的特征,因為它避免了導致訓練速度急劇
下降的梯度飽和,因此加快訓練過程。無下界有助于實現強I正則化效果(適當的擬合模
型)。(這個性質類似于ReLU和Swish的性質,其范圍是[≈0.31,[])
2.非單調函數:這種性質有助于保持小的負值,從而穩定網絡梯度流。大多數常用的激活
函數,如ReLU[f(x)=max(0,x)], Leaky ReLU[f(x)=max (0, x),1],由于其差分為0,
不能保持負值,因此大多數神經元沒有得到更新。
3.無窮階連續性和光滑性:Mish函數是光滑函數,具有較好的泛化能力和結果的有效優化
能力,可以提高結果的質量。
10.5 SwiGLU:自門控激活函數
10.5.1 為什么現在的大模型要高精度跑GeLU或SwiGLU,而不是改回ReLU跑低精度?
現在大模型往往是bf16或fp8跑矩陣乘法,但是激活函數都會用fl32來確保精度。
主要原因是,常用的激活函數如GeLU和SwiGLU都很復雜,低精度掉點非常顯著
GeLU和SwiGLU的優勢在于它們提供了更平滑、更豐富的非線性特征表達。
根據Shazeer(2020)的研究,SwiGLU相比于ReLU在Transforme架構+下能降低約1-2%的困惑
度,這種性能差距雖然看似不大,但對動輒幾十億甚至千億參數的LLM+而言,能帶來的性能收益
非常明顯。
至于的"低精度下掉點嚴重"的現象,確實存在。英特爾實驗室在FP8+超低精度訓練LLaMA+2-7B時
就發現,SwiGLU激活函數在長時間訓練后會出現非常嚴重的數直不穩定,具體表現為訓練后期loss
劇烈上升甚至訓練發散。分析顯示這是由于SwiGLU的門控機飛制極易放大激活輸出中的少數離群
值,這在FP8這種低精度下非常致命,最終導致梯度爆炸。
但值得注意的是,在稍高一些的精度(如BF16+)下,GeLU和SwiGLU并不會表現出明顯的性能下
降或者數值問題。谷歌的PaLM+、Meta的LLaMA訓練時都使用BF16精度,幾乎無性能損失(與
FP32相比誤差在統計波動范圍內)。也就是說BF16精度已經足以支撐GeLU/SwiGLU這類激活函數
的穩定訓練與推理。
那么問題來了,既然ReLU在低精度上數值更穩定(畢竟只涉及簡單的截斷操作,沒有復雜的指數或
高階函數),為什么大家還是不用呢?我認為ReLU的劣勢主要體現在兩個方面:
- 第一是早期觀念上的誤區,認為ReLU容易出現負值梯度為零導致的"神經元死亡"(deadReLU)
現象;但實際上在Transformer這種帶有LayerNorm+的架構里,ReLU死亡現象并不明顯,這一點最
近已經逐漸被學術界重新證實。- 第二個因素更關鍵:業界剛剛開始注意到ReLU的潛在優勢,比如激活值高稀疏性帶來的效率提
升。大船掉頭需要時間。Mirzadeh(2023)等人發現,使用ReLU激活后模型推理時可以跳過大量
的零值運算,FLOPs甚至可以減少30%~50%。他們在大模型微調實驗中驗證過,使用ReLU或其變
種(如ReGLU,Squared ReLU)替換原始的GeLU/SWiGLU,模型性能幾乎不受影響,但推理效率
卻能明顯提高。這種"回歸簡單激活函數"的思潮,已經在低資源推理場景(如BitNet)得到了實際驗證。BitNet就通
過ReLU搭配1-bit權重和8-bit激活,成功實現了Transformer模型的超低精度訓練和部署,且性能與
標準FP16模型幾乎持平。
所以綜合來看,目前大模型仍廣泛使用GeLU/SwiGLU激活函數更多是歷史延續及微小性能增益的綜
合結果,BF16精度足夠支撐它們的正常表現。只有在追求極致低精度部署(如FP8或更低)或更極
端的效率優化場景下,ReLU才開始重新受到關注。
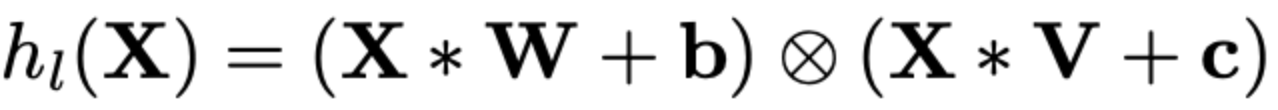
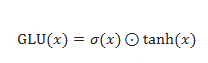

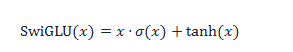


)


)










中取得成功)
商品管理)

