對于會有多次測量值的數據，用普通的回歸去插補，往往會忽略掉數據個體本身的特點，畢竟多次的測量值其實就代表了數據個體的不穩定性，存在額外的干擾。
而RE的插補原理是結合個體本身的隨機效應和群體的固體效應再加上截距進行插補的，比如學生A參加了月考，期中考，但是缺席了期末考，如果要插補期末考的成績，除了班級的教學質量之外，學生個體的學習能力也很關鍵，可能存在學生本身是學霸，成很穩定，也可能存在學生是中游水平，期中考試超常發揮，需要綜合考量。
以下是一個例子：
library(nlme)
library(ggplot2)
#?生成模擬數據：10個患者，每個患者測量3-5次
set.seed(123)n_patients?<-?10
time_points?<-?5#?創建數據框
data?<-?data.frame(patient_id?=?rep(1:n_patients,?each?=?time_points),time?=?rep(1:time_points,?times?=?n_patients),treatment?=?rep(rbinom(n_patients,?1,?0.5),?each?=?time_points)??#?治療組（0/1）
)#?生成因變量y（含隨機效應和噪聲）
data$y?<-?2?*?data$treatment?+?rep(rnorm(n_patients,?sd?=?1.5),?each?=?time_points)?+?rnorm(nrow(data),?sd?=?1)#?人為制造缺失值（MAR：缺失概率與時間相關）
data$y[data$time?>?3?&?runif(nrow(data))?>?0.7]?<-?NA
head(data,?15)#?擬合線性混合模型（LMM）
model?<-?lme(y?~?treatment?+?time,?random?=?~?1?|?patient_id,?data?=?data,?na.action?=?na.exclude)#?預測缺失值（插補）
data$y_imputed?<-?ifelse(is.na(data$y),?predict(model,?newdata?=?data),?data$y)#?查看插補結果
head(data[is.na(data$y),?c("patient_id",?"time",?"y",?"y_imputed")],?10)ggplot(data,?aes(x?=?time,?y?=?y_imputed,?group?=?patient_id,?color?=?factor(treatment)))?+geom_line(alpha?=?0.6)?+geom_point(aes(y?=?y),?size?=?2,?na.rm?=?TRUE)?+??#?原始觀測點（含缺失）labs(title?=?"RE插補效果（紅色點為原始觀測值）",?x?=?"時間",?y?=?"觀測值",?color?=?"治療組")?+theme_minimal()
輸出：
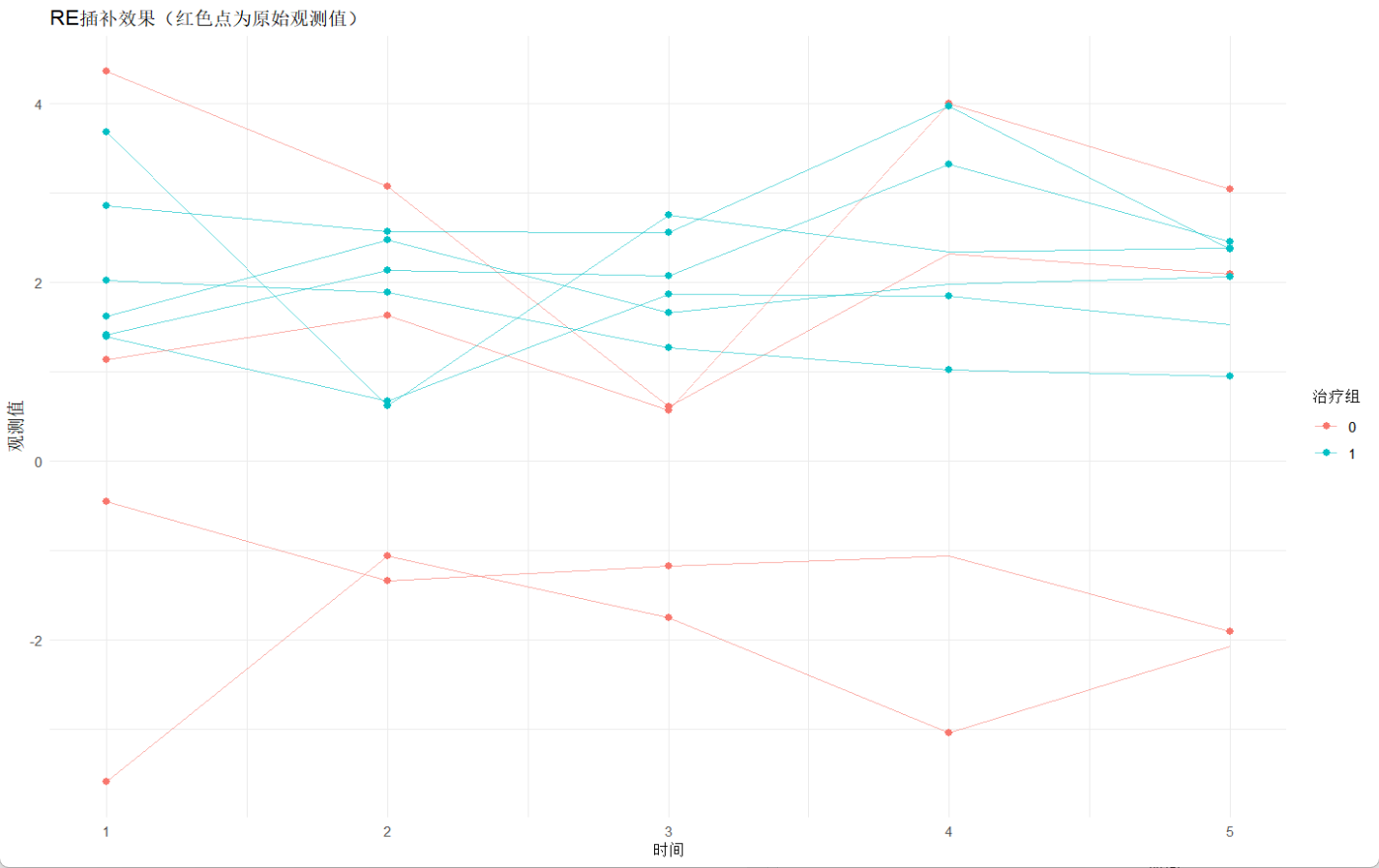
從圖中可以看到，盡管RE能考慮隨機效應加固體效應，但是如果樣本本身存在離散值或者波動比較大的話，那么不管用什么方法去插補效果都比較差。
)
