【圖像噪點消除】——圖像預處理（OpenCV）

1 均值濾波

2 方框濾波

3 高斯濾波

4 中值濾波

5 雙邊濾波

6 小結

噪聲：圖像中的一些干擾因素。通常是由于圖像采集設備、傳輸信道等因素造成的，表現為圖像中隨機的亮度。常見的噪聲類型有高斯噪聲和椒鹽噪聲。高斯噪聲是一種分布符合正態分布的在噪聲，會使圖像變得模糊或有噪點。椒鹽噪聲則是一些黑白色的像素值分布在原圖像上。


高斯噪聲	原圖	椒鹽噪聲

濾波器也叫卷積核，工作原理也是在原圖上進行滑動并計算中心像素點的像素值。分為線性濾波器和非線性濾波器，線性濾波器對領域中的像素進行線性運算，如在核的范圍內進行加權求和。常見的線性濾波器有均值濾波、高斯濾波等。非線性濾波器則是利用原始圖像與模板之間的一種邏輯關系得到結果，常見的非線性濾波器有中值濾波器、雙邊濾波器等/

濾波與模糊的練習與區別：

都屬于卷積，不同濾波方法之間知識卷積核的不同（對線性濾波而言）
低通濾波器是模糊，高通濾波器是銳化
低通濾波器就是允許低頻信號通過，在圖像中邊緣和噪點都相當于高頻部分，所以低通濾波器用于去除噪點、平滑和模糊圖像。高通濾波器則反之，用來增強圖像邊緣，進行銳化處理。

注意：椒鹽噪聲可以理解為斑點，隨機出現在圖像中的黑點或白點；高斯噪聲可以理解為拍攝圖片時由于光照等原因造成的噪聲。

1 均值濾波

最簡單的濾波處理，取得是卷積核區域內元素的均值，如3x3卷積核：

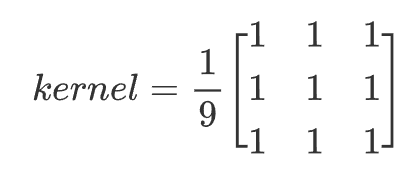
比如有一張4*4的圖片，現在使用一個3*3的卷積核進行均值濾波時，其過程如下所示：

對于邊界的像素點，則會進行邊界填充，以確保卷積核的中心能夠對準邊界的像素點進行濾波操作。在OpenCV中，默認的是使用BORDER_REFLECT_101的方式進行填充，下面的濾波方法中除了中值濾波使用的是BORDER_REPLICATE進行填充之外，其他默認也是使用這個方式進行填充，通過卷積核在原圖上從左上角滑動計算到右下角，從而得到新的4*4的圖像的像素值。

案例：

import cv2 as cv
img_old = cv.imread("./images/lvbo2.png")
img = cv.resize(img_old,(480,480))
img_jy = cv.imread("./images/lvbo3.png")
# 均值濾波：cv2.blur(img,ksize)
img_blur = cv.blur(img,(3,3),borderType=cv.BORDER_REFLECT_101)
cv.imshow("img",img)
cv.imshow("img_blur",img_blur)
cv.waitKey(0)
cv.destroyAllWindows()

輸出：


原圖	均值濾波

2 方框濾波

方框濾波跟均值濾波很像，如3×3的濾波核如下：

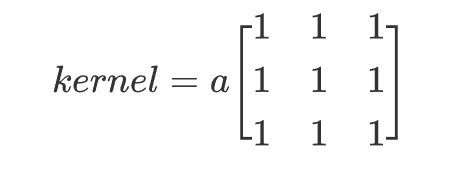
在濾波算法組件中，當參數filtering_method選為方框濾波時，參數component_param為ksize，ddepth,normalize。下面講解這3個參數的含義：

ksize：代表卷積核的大小，eg：ksize=3，則代表使用3×3的卷積核。

ddepth：輸出圖像的深度，-1代表使用原圖像的深度。
- 圖像深度是指在數字圖像處理和計算機視覺領域中，每個像素點所使用的位數（bit depth），也就是用來表示圖像中每一個像素點的顏色信息所需的二進制位數。圖像深度決定了圖像能夠表達的顏色數量或灰度級。
normalize：當normalize為True的時候，方框濾波就是均值濾波，上式中的a就等于1/9；normalize為False的時候，a=1，相當于求區域內的像素和。


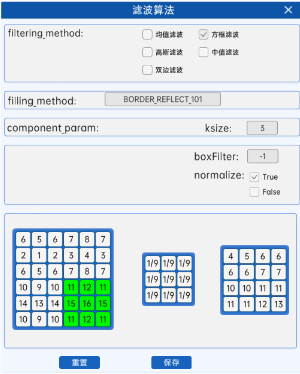normalize=True	normalize=False

案例：

import cv2 as cv
img_old = cv.imread("./images/lvbo2.png")
img = cv.resize(img_old,(480,480))
img_jy = cv.imread("./images/lvbo3.png")# 方框濾波：cv2.boxFilter(img,ddepth,ksize,normalize)
img_box1 = cv.boxFilter(img,-1,(3,3),normalize=True)# 相當于均值濾波
img_box2 = cv.boxFilter(img,-1,(3,3),normalize=False) # 把區域內的像素值全部相加
cv.imshow("img_box2",img_box2)
cv.waitKey(0)
cv.destroyAllWindows()

輸出：


原圖	方框濾波

3 高斯濾波

高斯濾波是一種常用的圖像處理技術，主要用于平滑圖像、去除噪聲。它通過使用高斯函數（正態分布）作為卷積核來對圖像進行模糊處理。

高斯濾波的卷積核權重并不相同：中間像素點權重最高，越遠離中心的像素權重越小。還記得我們在自適應二值化里是怎么生成高斯核的嗎？這里跟自適應二值化里生成高斯核的步驟是一樣的，都是以核的中心位置為坐標原點，然后計算周圍點的坐標，然后帶入下面的高斯公式中。

$g(x,y)=\frac{1}{2\pi\sigma^{2}}e^{-\frac{(x^{2}+y^{2})}{2\sigma^{2}}}$

其中，x和 y 是相對于中心點的坐標偏移量，σ 是標準差，控制著高斯函數的寬度和高度。較大的 σ 值會導致更廣泛的平滑效果。

卷積核通常是一個方形矩陣，其元素值根據高斯函數計算得出，并且這些值加起來等于1，近似于正態分布，以確保輸出圖像的亮度保持不變。

其中的值也是與自適應二值化里的一樣，當時會取固定的系數，當kernel大于7并且沒有設置時，會使用固定的公式進行計算 $\sigma$ 的值：

$\sigma=0.3*\left((k s i z e-1)*0.5-1\right)+0.8$

我們還是以3*3的卷積核為例，其核值如下所示：

得到了卷積核的核值之后，其濾波過程與上面兩種濾波方式的濾波過程一樣，都是用卷積核從圖像左上角開始，逐個計算對應位置的像素值，并從左至右、從上至下滑動卷積核，直至到達圖像右下角，唯一的區別就是核值不同。

在濾波算法組件中，當參數filtering_method選為高斯濾波，參數component_param為ksize，sigmaX。下面講解這2個參數的含義：

ksize：代表卷積核的大小，eg：ksize=3，則代表使用3×3的卷積核。

sigmaX：就是高斯函數里的值，σx值越大，模糊效果越明顯。高斯濾波相比均值濾波效率要慢，但可以有效消除高斯噪聲，能保留更多的圖像細節，所以經常被稱為最有用的濾波器。均值濾波與高斯濾波的對比結果如下（均值濾波丟失的細節更多）：

案例：

import cv2 as cv
img_old = cv.imread("./images/lvbo2.png")
img = cv.resize(img_old,(480,480))
img_jy = cv.imread("./images/lvbo3.png")# 高斯濾波：cv2.GaussianBlur(img,ksize,sigmax)
img_gauss = cv.GaussianBlur(img,(3,3),0.5)
# cv.imshow("img_gauss",img_gauss)
cv.waitKey(0)
cv.destroyAllWindows()

輸出：


原圖	高斯濾波

4 中值濾波

中值又叫中位數，是所有數排序后取中間的值。中值濾波沒有核值，而是在原圖中從左上角開始，將卷積核區域內的像素值進行排序，并選取中值作為卷積核的中點的像素值，其過程如下所示：

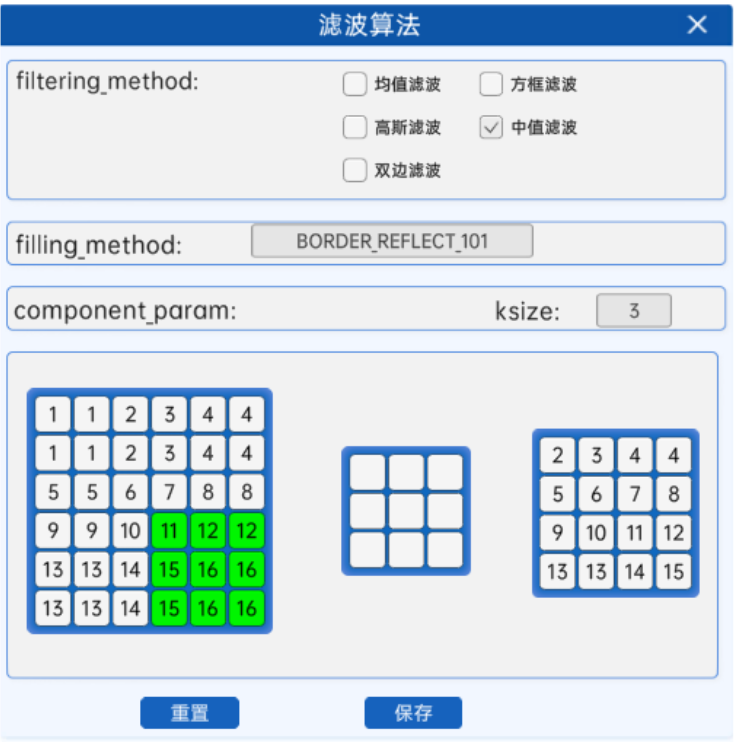
中值濾波就是用區域內的中值來代替本像素值，所以那種孤立的斑點，如0或255很容易消除掉，適用于去除椒鹽噪聲和斑點噪聲。中值是一種非線性操作，效率相比前面幾種線性濾波要慢。

比如下面這張斑點噪聲圖，用中值濾波顯然更好：

在濾波算法組件中，當參數filtering_method選為中值濾波，參數component_param為ksize，代表卷積核的大小，eg：ksize=3，則代表使用3×3的卷積核。

案例：

import cv2 as cv
img_old = cv.imread("./images/lvbo2.png")
img = cv.resize(img_old,(480,480))
img_jy = cv.imread("./images/lvbo3.png")
# 中值濾波：cv2.medianBlur(img,ksize)
img_median = cv.medianBlur(img_jy,3)
cv.imshow("img_jy",img_jy)
cv.imshow("img_median",img_median)
cv.waitKey(0)
cv.destroyAllWindows()

輸出：


原圖	中值濾波

5 雙邊濾波

模糊操作基本都會損失掉圖像細節信息，尤其前面介紹的線性濾波器，圖像的邊緣信息很難保留下來。然而，邊緣（edge）信息是圖像中很重要的一個特征，所以這才有了雙邊濾波。

可以看到，雙邊濾波明顯保留了更多邊緣信息，下面來介紹一下雙邊濾波。

雙邊濾波的基本思路是同時考慮將要被濾波的像素點的空域信息（周圍像素點的位置的權重）和值域信息（周圍像素點的像素值的權重）。為什么要添加值域信息呢？是因為假設圖像在空間中是緩慢變化的話，那么臨近的像素點會更相近，但是這個假設在圖像的邊緣處會不成立，因為圖像的邊緣處的像素點必不會相近。因此在邊緣處如果只是使用空域信息來進行濾波的話，得到的結果必然是邊緣被模糊了，這樣我們就丟掉了邊緣信息，因此添加了值域信息。

雙邊濾波采用了兩個高斯濾波的結合，一個負責計算空間鄰近度的權值（也就是空域信息），也就是上面的高斯濾波器，另一個負責計算像素值相似度的權值（也就是值域信息），也是一個高斯濾波器。其公式如下所示：

$g(i,j)=\frac{\sum_{(k,l)\in S(i,j)}f(k,l)\omega(i,j,k,l)}{\Sigma_{(k,l)\in S(i,j)}\omega(i,j,k,l)}$

其中，

$S(i,j)$ ：指以 $(i,j)$ 為中心的鄰域的范圍

$f(k,l)$ ：輸入的點的像素值，也就是在原始圖像中位置 $(k,l)$ 的像素值。

$\omega(i,j,k,l)$ ：這是權重函數，它決定了位置 $(k,l)$ 的像素值 $f(k,l)$ 對位置 $(i,j)$ 的貢獻程度。
$g(i,j)$ ：表示中心點 $(i,j)$ 的像素值，也就是經過雙邊濾波處理后，在位置 $(i,j)$ 的像素值。
分子： $\sum (k,l)\in S(i,j)f(k,l)\omega (i,j,k,l)$
- 這是對鄰域內所有像素值 $f(k,l)$ 與其對應的權重 $\omega (i,j,k,l)$ 的乘積求和。這一步計算了加權后的像素值總和。
分母： $\sum (k,l)\in S(i,j)\omega (i,j,k,l)$
- 這是對鄰域內所有像素的權重 $\omega (i,j,k,l)$ 求和。這一步計算了權重的總和。
計算過程：
1. 確定鄰域：選擇一個以 $(i,j)$ 為中心的鄰域 $S(i,j)$ 。
2. 計算權重：對于鄰域內的每個像素 $(k,l)$ ，計算其權重 $\omega (i,j,k,l)$ 。
3. 加權求和：將鄰域內每個像素值 $f(k,l)$ 與其權重 $\omega (i,j,k,l)$ 相乘，并對所有乘積求和。
4. 歸一化：將加權求和的結果除以權重總和，得到最終的像素值 $g(i,j)$ 。

上述公式我們進行轉化，假設公式中 $\omega(i,j,k,l)$ 為 $m$ ，則有

$g(i,j)=\frac{f_{1}\cdot m_{1}+f_{2}\cdot m_{2}+\dots+f_{n}\cdot m_{n}}{m_{1}+m_{2}+\dots+m_{n}}$

設 $m_{1}+m_{2}+\cdots+m_{n}=M$ ，則有

$g(i,j)=f_{1}\cdot{\frac{m_{1}}{M}}+f_{2}\cdot{\frac{m_{2}}{M}}+\cdots+f_{n}\cdot{\frac{m_{n}}{M}}$

此時可以看到，這與上面的濾波中計算過程已經一模一樣了， $\frac{m_{1}}{M}$ 就代表了第一個點的權重。接下來我們看看 $\omega(i,j,k,l)$ 是怎么來的，令

$\omega(i,j,k,l)=w_{s}*w_{r}$

而
$\omega_{s}=e^{-{\frac{(i-k)^{2}+(j-l)^{2}}{2\sigma_{s}{}^{2}}}}$
$\omega_{r}=e^{-{\frac{\|f(i,j)-f(k,l)\|^{2}}{2\sigma_{r}{}^{2}}}}$

可以看到，對于 $\omega_{S}$ 來說，這就是普通的高斯濾波函數，其帶入的坐標是坐標值， ${\boldsymbol{\sigma}}_{s}$ 是程序輸入值，該函數是在空間臨近度上計算的。而 $\omega_{r}$ 是計算像素值相似度，也是高斯函數帶入坐標值，然后得到對應點的像素值，進行兩個點像素值插值的絕對值的平方。也就是說，雙邊濾波的核值不再是一個固定值，而是隨著濾波的過程在不斷發生變化的。

在本實驗中的濾波算法組件中，當參數filtering_method選為雙邊濾波，參數component_param為ksize，d，sigmaColor，sigmaSpace，下面講解這4個參數的含義：

ksize：卷積核的大小
d：過濾時周圍每個像素領域的直徑，這里已經設置了核大小。d=9===>9x9
sigmaColor：在color space（色彩空間）中過濾sigma。參數越大，那些顏色足夠相近的的顏色的影響越大。較大的sigmaColor值意味著更大的顏色差異將被允許參與到加權平均中，從而使得顏色相近但不完全相同的像素也能夠相互影響。
sigmaSpace：在coordinate space（坐標空間）中過濾sigma。這個參數是坐標空間中的標準差，決定了像素位置對濾波結果的影響程度。它定義了在圖像的空間域中，一個像素可以影響周圍像素的最大距離。換句話說，它控制著濾波器作用的范圍大小。

關于2個sigma參數：

簡單起見，可以令2個sigma的值相等；

如果他們很小（小于10），那么濾波器幾乎沒有什么效果；

如果他們很大（大于150），那么濾波器的效果會很強，使圖像顯得非常卡通化。

關于參數d：

過大的濾波器（d>5）執行效率低。

對于實時應用，建議取d=5；

對于需要過濾嚴重噪聲的離線應用，可取d=9；

案例：

import cv2 as cv
img_old = cv.imread("./images/lvbo2.png")
img = cv.resize(img_old,(480,480))
img_jy = cv.imread("./images/lvbo3.png")# 雙邊濾波：使用兩個高斯核
img_bilate = cv.bilateralFilter(img_jy,9,140,140)
cv.imshow("img_bilate",img_bilate)
cv.waitKey(0)
cv.destroyAllWindows()

輸出：