一、排序算法的概念

????????排序（Sorting）是指：將一組“無序”的數據，按照某種“順序規則”排列成“有序”的過程。

1、按排序順序分類：

????????升序：從小到大排列，如 1, 3, 5, 7, 9

• 降序：從大到小排列，如 9, 7, 5, 3, 1

2、按排序方式分類：

二、 常見的排序算法及其特點

三、排序算法的應用場景

1. 數據庫系統：

   • 排序是實現?ORDER BY?的核心

   • 排序有助于數據壓縮和索引創建

2. 搜索優化：

   • 排序之后可以使用二分查找，大幅提高搜索效率

   數據分析和可視化：

3. • 排序能幫助找出最大/最小值、前 K 大數等

   • 排序數據更容易圖表化展示

4. 去重和統計：

   ? ? ? ? ? 排序后相同數據聚集在一起，方便統計頻率或去重

5. 工程開發：

   ? ? ? ? ? 排序是實現自動推薦、頁面排名、調度優化等系統的基礎

四、常用排序算法的實現

? ? ? ? 1、冒泡排序🫧

? ? ? ? 不斷比較鄰近的元素，將大元素右移，最終排成升序序列

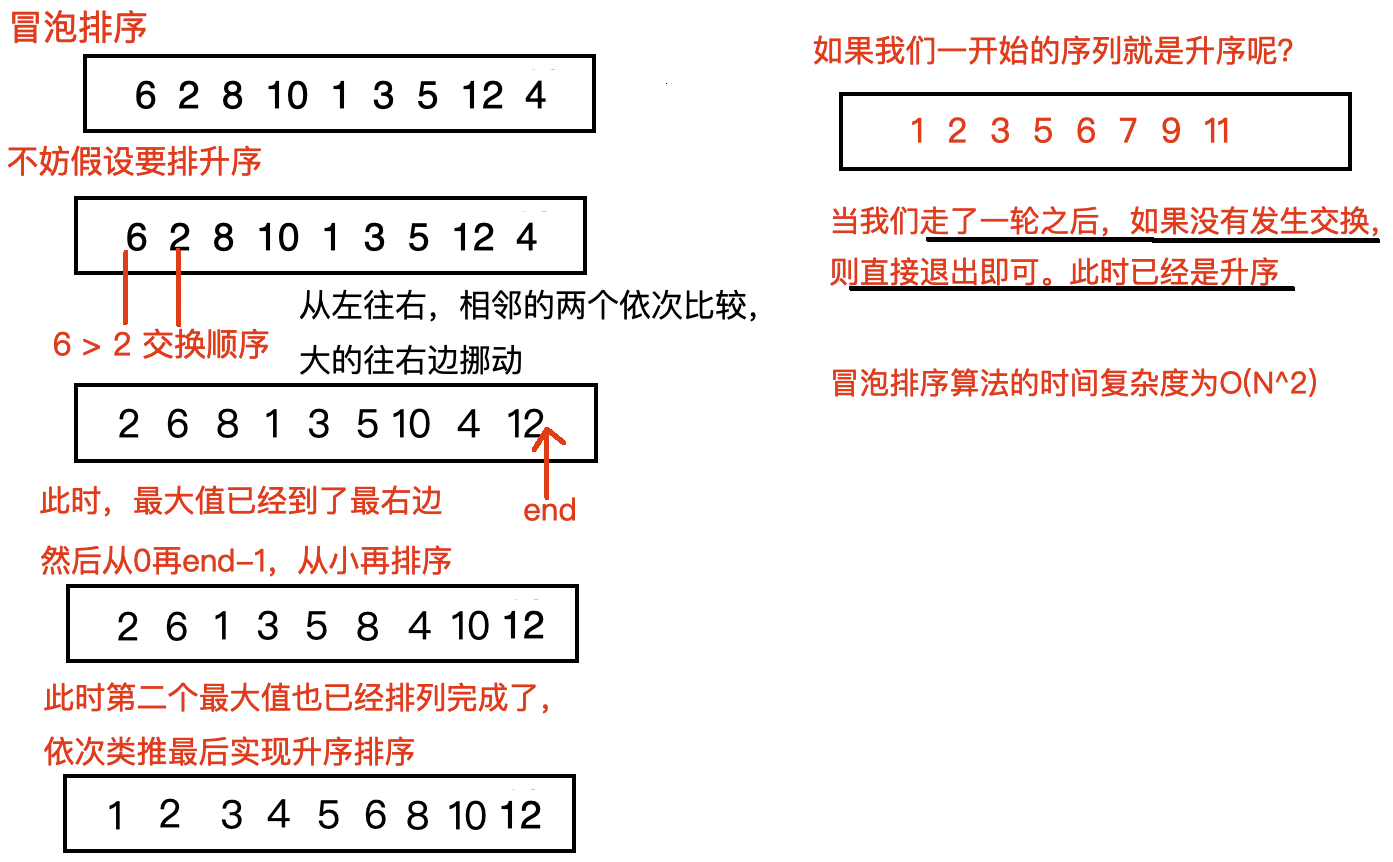
代碼實現：

void Swap(int* p,int* q){assert(p&&q);int tmp = *p;*p = *q;*q = tmp;return;
}void Bubble_sort(int* arr,int size){assert(arr);int end = size-1;int flag = 0;for (int i = 0;i<end;i++){for(int j = 0;j<end-i;j++){if(arr[j]>arr[j+1]){Swap(&arr[j],&arr[j+1]);flag = 1;}}if(flag == 0){break;}}return;
}//測試函數
int main(){int arr[]= {6,2,8,10,1,3,5,12,4};Bubble_sort(arr,9);for(int i = 0;i<9;i++){printf("%d ",arr[i]);}
}

冒泡排序的時間復雜度為，空間復雜度。

2、插入排序

????????將數組的每個元素與所在位置之前的元素比較，找到升序（降序）位插入即可。

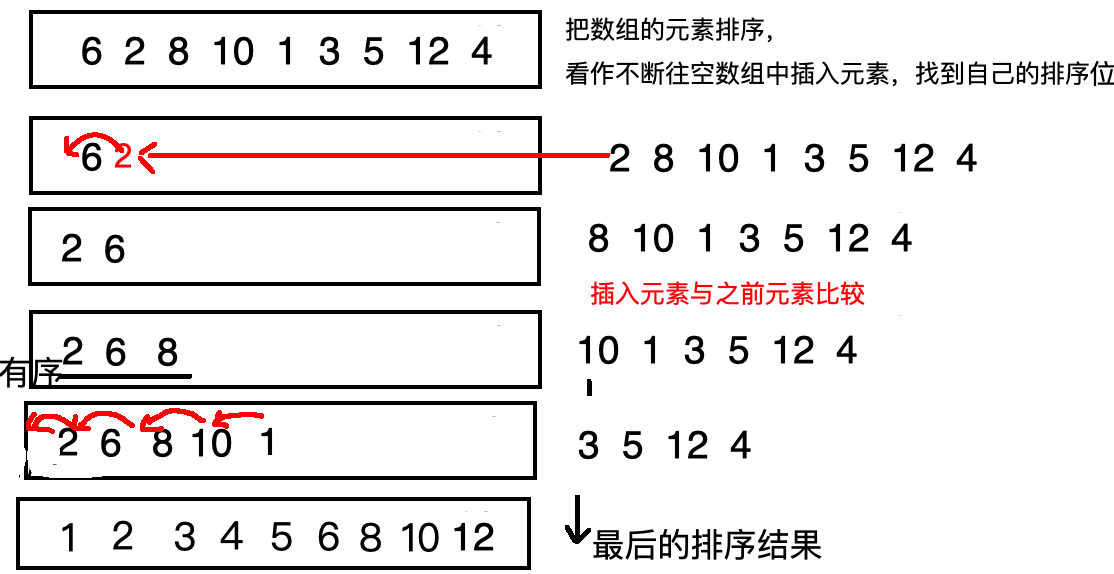
代碼實現：

void Insert_Sort(int* arr,int size){assert(arr);for (int end = 1;end<size;end++){for(int j = end-1;j>=0;j--){if(arr[j+1]<arr[j]){Swap(&arr[j],&arr[j+1]);}else{break;}}}
}int main(){int arr[]= {6,2,8,10,1,3,5,12,4};// Bubble_sort(arr,9);Insert_Sort(arr,9);for(int i = 0;i<9;i++){printf("%d ",arr[i]);}
}

插入排序的時間復雜度為，空間復雜度。

3、希爾排序的基本思想

希爾排序的提出者是 Donald Shell（1959 年），它是第一個突破 O(n2)?時間復雜度的排序算法。

核心思想：

將原始數組按照某個間隔 gap 進行“分組”，每組分別進行插入排序，然后逐步減小 gap，最終 gap = 1 時再進行一次插入排序，完成排序。

希爾排序的步驟說明（以升序為例）

1. 選擇一個初始間隔 gap，通常是數組長度的一半，如?gap = n/2

2. 將數組劃分為?gap?個子序列（組內元素間隔為 gap）

3. 對每個子序列進行插入排序

4. 縮小 gap：gap = gap / 2

5. 重復步驟 2～4，直到?gap = 1

思維導圖

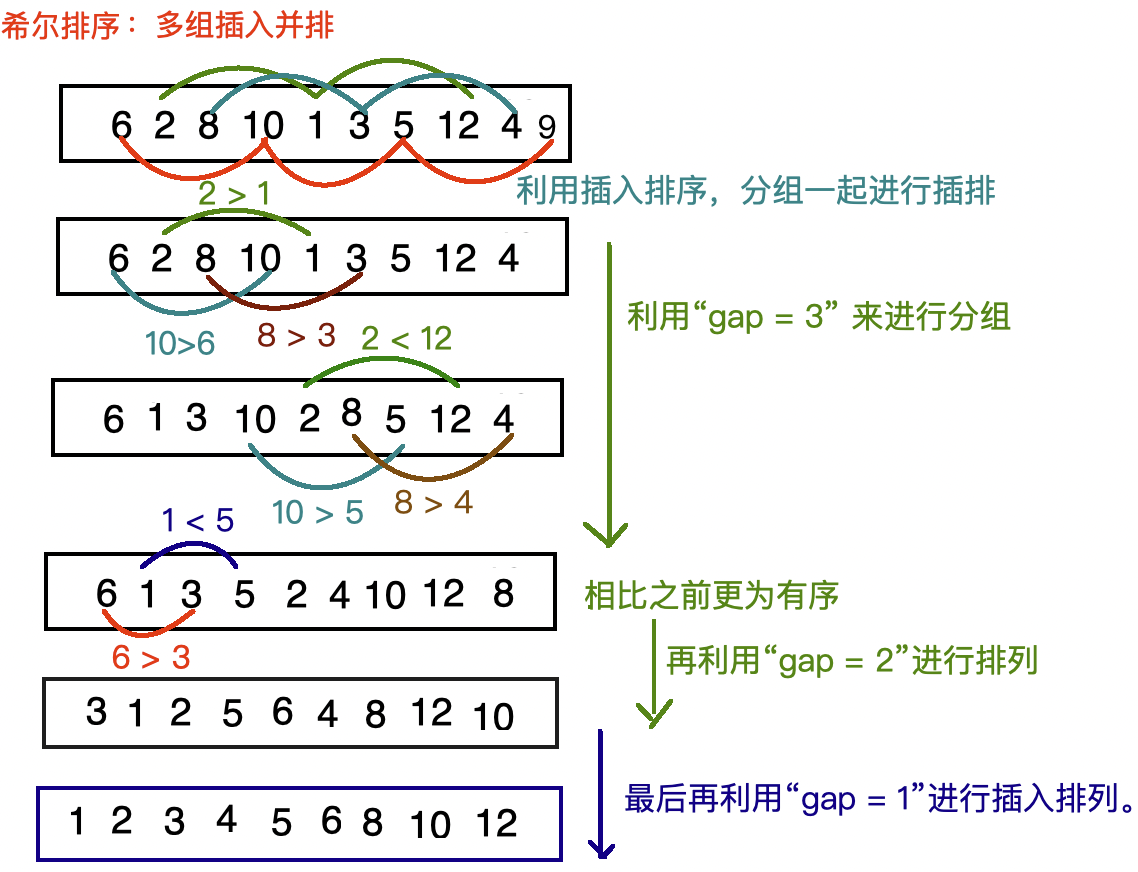
代碼實現：

void Shell_Sort(int* arr,int size){assert(arr);int gap = size;while(gap > 1){gap = gap/3+1;for (int end = gap;end<size;end++){int j = end-gap;int tmp = arr[end];while (j>=0 && arr[j]>tmp){arr[j+gap] = arr[j];j -= gap;}arr[j+gap] = tmp;}  }
}

希爾排序的時間復雜度：最壞情況視 gap 序列而定，常見為 O(n^(1.3 ~ 2))，比 O(n2) 快很多

希爾排序的特點

希爾排序與插入排序的對比

好了本期的排序算法內容分享就到這里結束了，謝謝大家的點贊收藏