CS231n-2017 Lecture4神經網絡筆記

神經網絡：

我們之前的線性分類器可以接受輸入，進而給出評分，這是一種線性變換，再此基礎上，我們對這種線性變換結果進行非線性變換，并輸入到下一層線性分類器中，這個過程就像是人類大腦神經的運作一樣，神經元接受信號，并輸出神經遞質給下一個神經元，表示是興奮（正權重）/抑制（負權重）

激活函數：

上文提到的非線性變換，即使用激活函數，顯然激活函數是非線性函數

常用的激活函數如下：

1.Sigmoid函數

$\sigma(x) = \frac{1}{1+e^{-x}}$

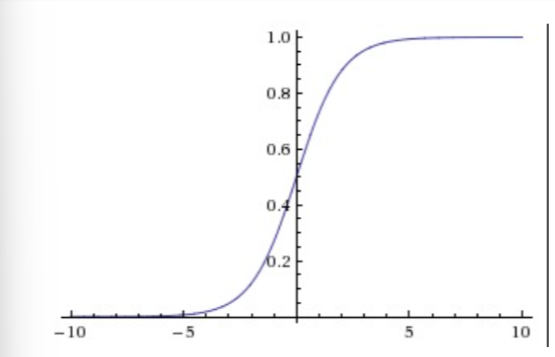
這個函數接受實數值，并將很大的負數變為0（抑制信號），很大的正數變為1（興奮信號）

但在實際上已經很少使用，主要是因為以下兩個缺點：

(1) Sigmoid函數飽和會使梯度消失

當激活函數的輸出接近0或者接近1時，這里的局部梯度幾乎為0，這就會導致一個問題，在反向傳播的時候，我們要求的梯度會與這里的局部梯度相乘，從而導致要求的梯度為0，所謂梯度消失，則這個梯度對應的變量的信號將無法再傳遞

同時，為了防止這種飽和，需要在初始化權重矩陣時特別小心，否則就會導致很多神經元過飽和，神經網絡無法再繼續學習

(2) Sigmoid函數的輸出不是以0為中心的

由于后續的神經元會以前面神經元的激活函數輸出作為輸入，導致其接收的輸入總是正數，那么在反向傳播的時候，會導致梯度要么全為正數，要么全為負數（比如對于 $f = Wx+b, x>0$ ?,會導致 $\nabla_Wf>0$ ），這會導致梯度下降權重更新的時候忽然很大的正向忽然很大的負向所產生的z字形的下降。不過，在整個batch的數據的梯度被加起來后，對于權重的最終更新會有不同的正負，這樣就一定程度地減輕了這個問題

2.Tanh函數

$tanh(x) = 2\sigma(2x) - 1 = \frac{e^x-e^{-x}}{e^x+e^{-x}}$

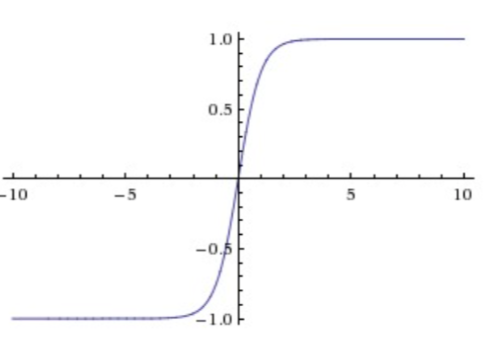
這個函數將實數值壓縮到 $[-1,1]$ ?之間

它也存在飽和問題，但和sigmoid函數不同的是，它的輸出是以0為中心的

3.ReLU函數

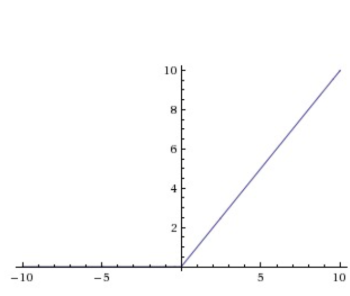
$ReLU(x) = \begin{cases} 0\text{,} & x<0 \\ x\text{,}& otherwise \end{cases}$

優點：

1.相較于Sigmoid和Tanh，ReLU對隨機梯度下降的收斂有巨大的加速作用

2.ReLU的計算資源開銷較少，只需要對矩陣進行閾值計算得到

缺點：

當很大的梯度經過ReLU的神經元時，梯度下降將x更新至負數或者接近0，那么就會損失掉這個神經元的梯度，導致其死亡

這種情況在學習率較高的時候出現頻率較高，由于步長過長，導致x在一次權重更新時就下降到0

4.Leaky ReLU

為了解決ReLU的死亡問題，我們對其進行改進，使公式變為

$Leaky ReLU(x) = \begin{cases} 1\text{ ,}& x<0\\ 1+\alpha x\text{,}& otherwise \end{cases}$

其中 $\alpha$ ?是一個小常量

5.Maxout函數

$Maxout = max{(W_1x+b_1,W_2x+b_2)}$

可以發現ReLU是Maxout的特殊情況，即 $W_1 = 0, b_1 = 0$

則Maxout擁有ReLU的所有優點，而沒有其缺點

但由于 $W_1,b_1$ 的存在，它每個神經元的參數都增加了一倍

激活函數的選擇問題：

通常建議使用ReLU，并注意設置學習率，監控網絡中死亡神經元的比例，若死亡比例較高，則可以嘗試使用Leaky ReLU或Maxout，也可以嘗試tanh，但不推薦sigmoid

神經網絡結構：

層狀結構：

神經網絡被建模成神經元的集合，神經元之間以無環圖的形式連接，通常是分層的，最普通的是全連接層(fully-connected layer)，全連接層中的神經元與其前后兩層的神經元是完全成對連接的，但在同一個全連接層的神經元之間沒有連接，如圖：

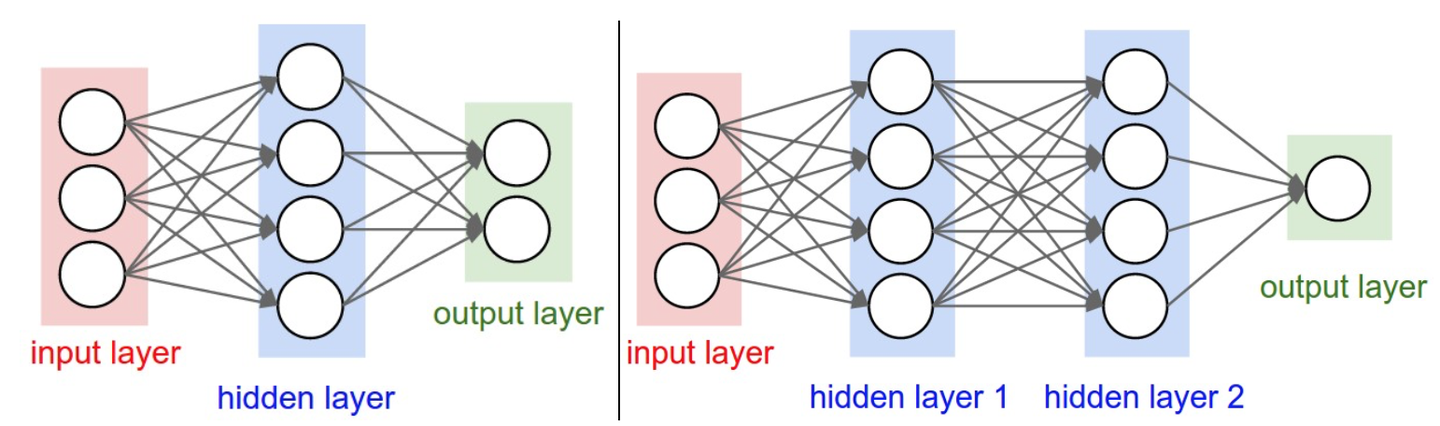
命名規則：

當我們說N層神經網絡的時候，不把輸入層算作一層

可使用ANN(Artificial Neural Networks)或MLP(Multi-Layer Perceptrons)來指代神經網絡

輸出層：

輸出層通常沒有激活函數

網絡尺寸：

衡量神經網絡尺寸的標準有兩個：

1.神經元的個數

2.參數的個數

以上圖舉例

第一個網絡有4+2=6個神經元（不算輸入層）， $3\times4+4\times2=20$ ?個權重參數，還有4+2=6個偏置，共26個可學習的參數

同理，第二個網絡有41個可學習的參數

神經網絡前向傳播計算舉例：

將神經網絡組成層狀，會方便我們使用矩陣乘法進行前向傳播，以上圖右邊的神經網絡舉例

輸入是 $[3\times1]$ ?的向量，一個層所有連接的權重可以儲存在一個矩陣中，比如第一個隱藏層的權重矩陣是一個 $[4\times3]$ ?的矩陣 $W_1$ ，偏置是 $[4\times1]$ ?的向量 $b_1$ ，假設第一層的激活函數為f，則 $f(W_1x+b_1)$ ?即可得到第一個隱藏層的輸出，后面幾層的運算同理

表達能力：

可以這樣來理解具有全連接層的神經網絡，它們定義了一個由一系列函數組成的函數族，網絡的權重就是每個函數的參數，已被證明，給出任意連續函數 $f(x)$ ?和任意 $\epsilon>0$ ?，均存在至少含1個隱藏層的神經網絡 $g(x)$ ?, 使得 $|f(x) - g(x)|< \epsilon$ ?即神經網絡可以近似任何連續函數

既然2層神經網絡可以完美近似所有連續函數，那為什么需要將網絡做得更深層呢？這是因為淺層網絡實際訓練效果較差

神經網絡在實踐中好用，是因為其表達出的函數不僅平滑，而且對于數據的統計特性有很好的擬合

但對于普通神經網絡來說，層數并不是越多越好，其會面臨梯度消失難以訓練的問題，但對于卷積神經網絡來說，層數是一個極為重要的因素，一個直觀解釋是，因為圖像具有層次化結構，所以需要多層處理這種數據

如何設置層的數量和尺寸：

更大容量的神經網絡可以表達更復雜的函數，但這既是優點也是缺點，優點是其可以分類更復雜的數據，缺點是可能造成對訓練數據的過擬合

過擬合指的是網絡對數據中的噪聲有很強的擬合能力，而沒有重視數據間的潛在基本關系（假設的），例如，下圖中使用20個隱藏層的網絡擬合了所有訓練數據，但代價是把決策邊界變成了許多不相連的紅綠區域，即沒有忽略異常點的噪聲，而另外兩個網絡擬合的決策邊界就較為寬泛，這樣在實際測試中會有更好的泛化能力

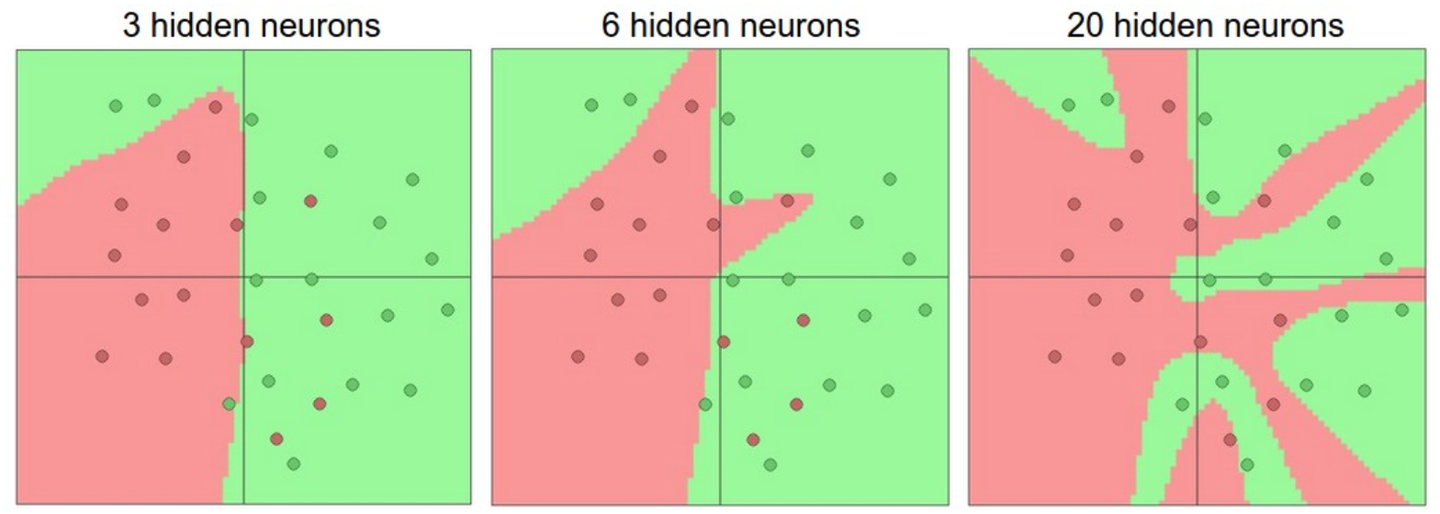
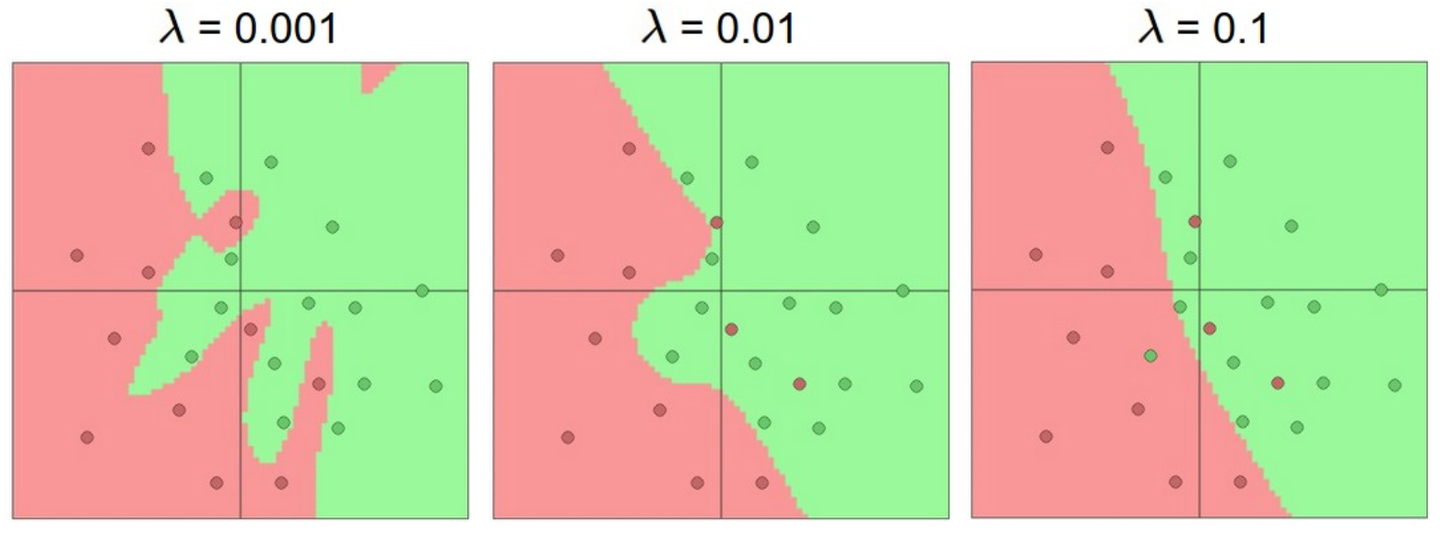
但并不是不提倡使用大容量的神經網絡，小網絡更難使用梯度下降等局部方法來訓練，而大網絡效果更好。因此我們應該想別的辦法來避免過擬合，例如在Loss函數中加入正則化，下圖是20隱藏層網絡正則化超參數取不同值時的訓練效果

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/92133.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/92133.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/92133.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！