---

1.摘要

傳統DBO存在探索與開發能力失衡、求解精度低以及易陷入局部最優等問題。因此，本文提出了帶有縮減因子分數階蜣螂優化算法（FORDBO），其通過縮減因子實現探索與開發能力的動態平衡。分數階微積分策略用于調整搜索區域邊界，使算法能更有效地聚焦于潛在的優質解空間。此外，重復更新機制進一步增強了跳出局部最優的能力。

2.蜣螂優化算法DBO原理

【智能算法】蜣螂優化算法（DBO）原理及實現

3.改進策略

縮減因子

DBO在探索與開發能力的平衡上存在不足，容易出現全局探索不充分或局部開發不精確的問題，參數的隨機選取也會導致優化過程不穩定。為解決這些問題，本文引入了自適應縮減因子$w$，實現了縮減因子的動態調整。
$$w={\mathrm{e}}^{?\frac{b}{k^a}\frac{t}{T_{\max }}}$$

在滾球蜣螂階段，個體更新：
$${\mathbf{x}}_i(t+1)=w{\mathbf{x}}_i(t)+\alpha k{\mathbf{x}}_i(t?1)+b\Delta \mathbf{x}$$
$${\mathbf{x}}_i(t+1)=w{\mathbf{x}}_i(t)+\tan \theta \left|{\mathbf{x}}_i(t)?{\mathbf{x}}_i(t?1)\right|$$

動態邊界的分數階調整

DBO上下邊界會隨著迭代動態收縮，從而提升搜索的精度。但隨著邊界的不斷收窄，種群個體容易集中甚至重疊，導致多樣性下降，影響全局優化能力。此外，當前邊界的調整僅依賴于當前迭代次數以及局部和全局最優解的位置，缺乏對歷史邊界信息的繼承和利用，進一步限制了優化效果。采用G-L定義：
$$D^v[f(x)]=\underset{\omega \to 0}{\lim }{\omega }^{?v}\sum _{k=0}^{\beta }(?1{)}^k\frac{\Gamma (v+1)}{\Gamma (k+1)\Gamma (v?k+1)}f(x?k\omega )$$

化簡可得：
$$D^{\nu }\left[L{b}^{?}(t+1)\right]=\left(\frac{1}{T_{\text{max}}}\right){\mathbf{X}}^{?}$$
$$D^{\nu }\left[U{b}^{?}(t+1)\right]=?\left(\frac{1}{T_{\text{max}}}\right){\mathbf{X}}^{?}$$

重復更新機制

重復更新機制通過對全局最優個體的位置進行多次迭代更新，結合局部最優和群體平均信息，并引入概率性多樣化操作，有效提升了算法跳出局部最優的能力。

4.結果展示

這里采用fes對FORDBO測試（原文iter，增加DE冠軍算法）

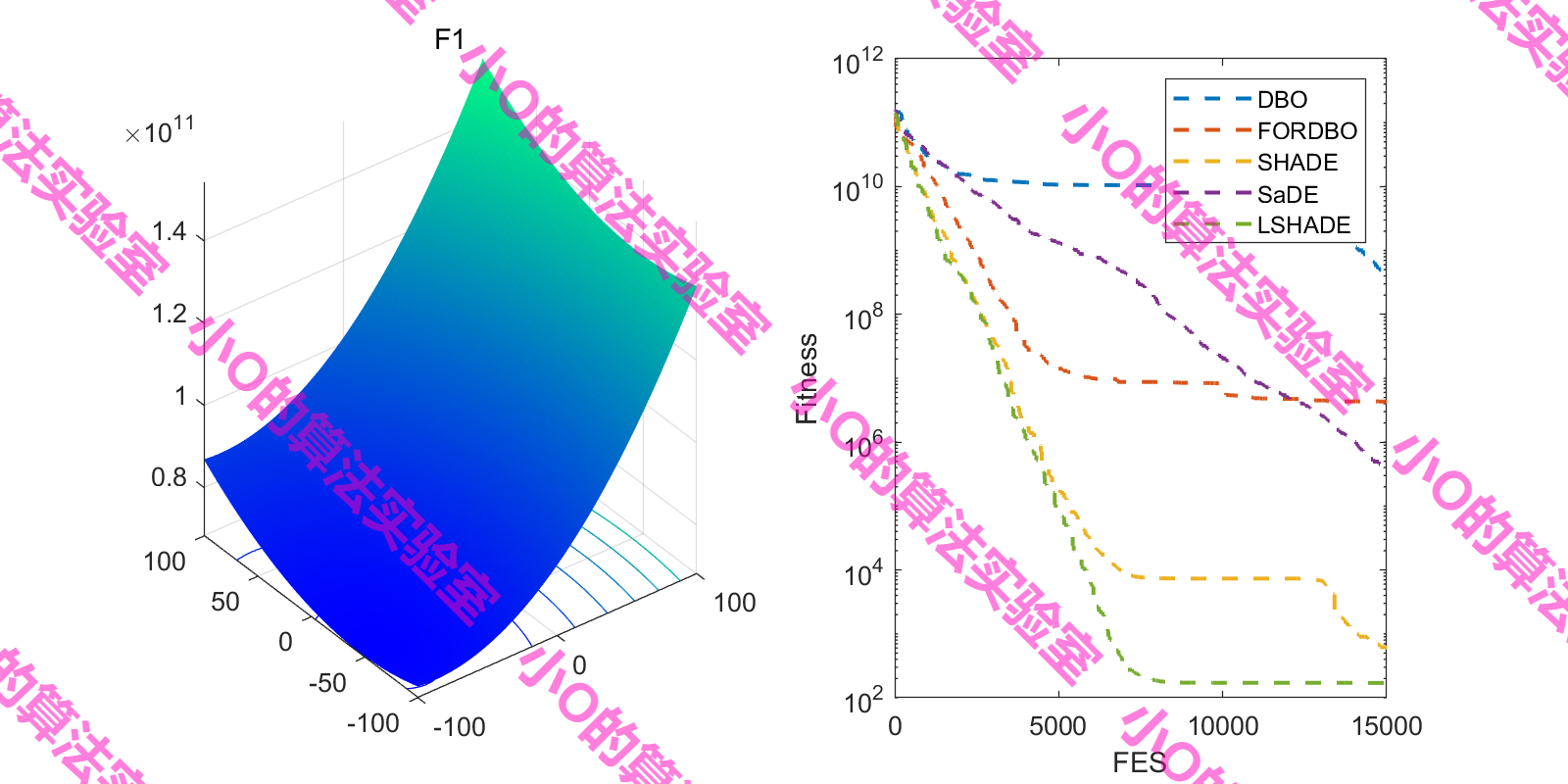
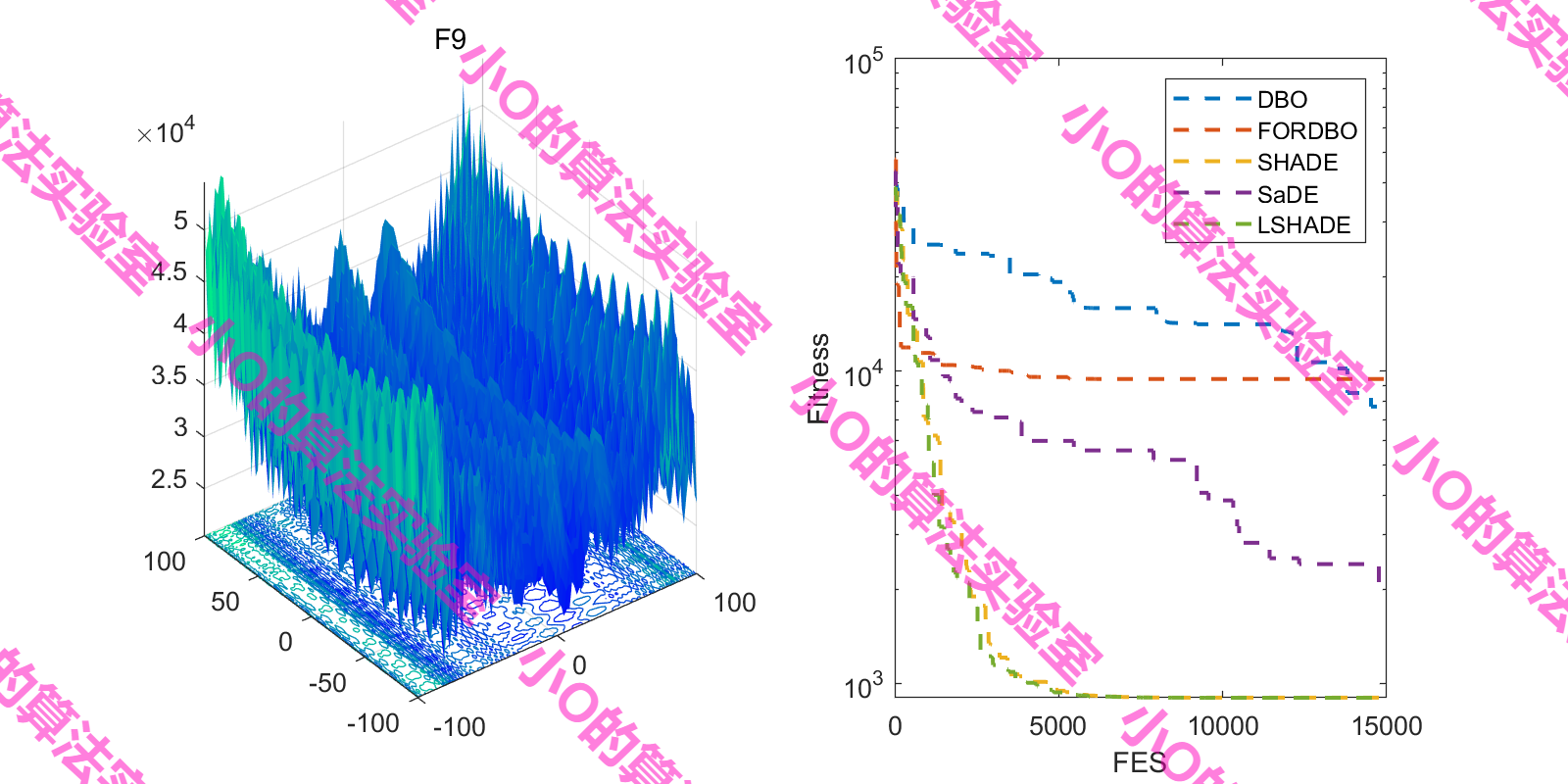
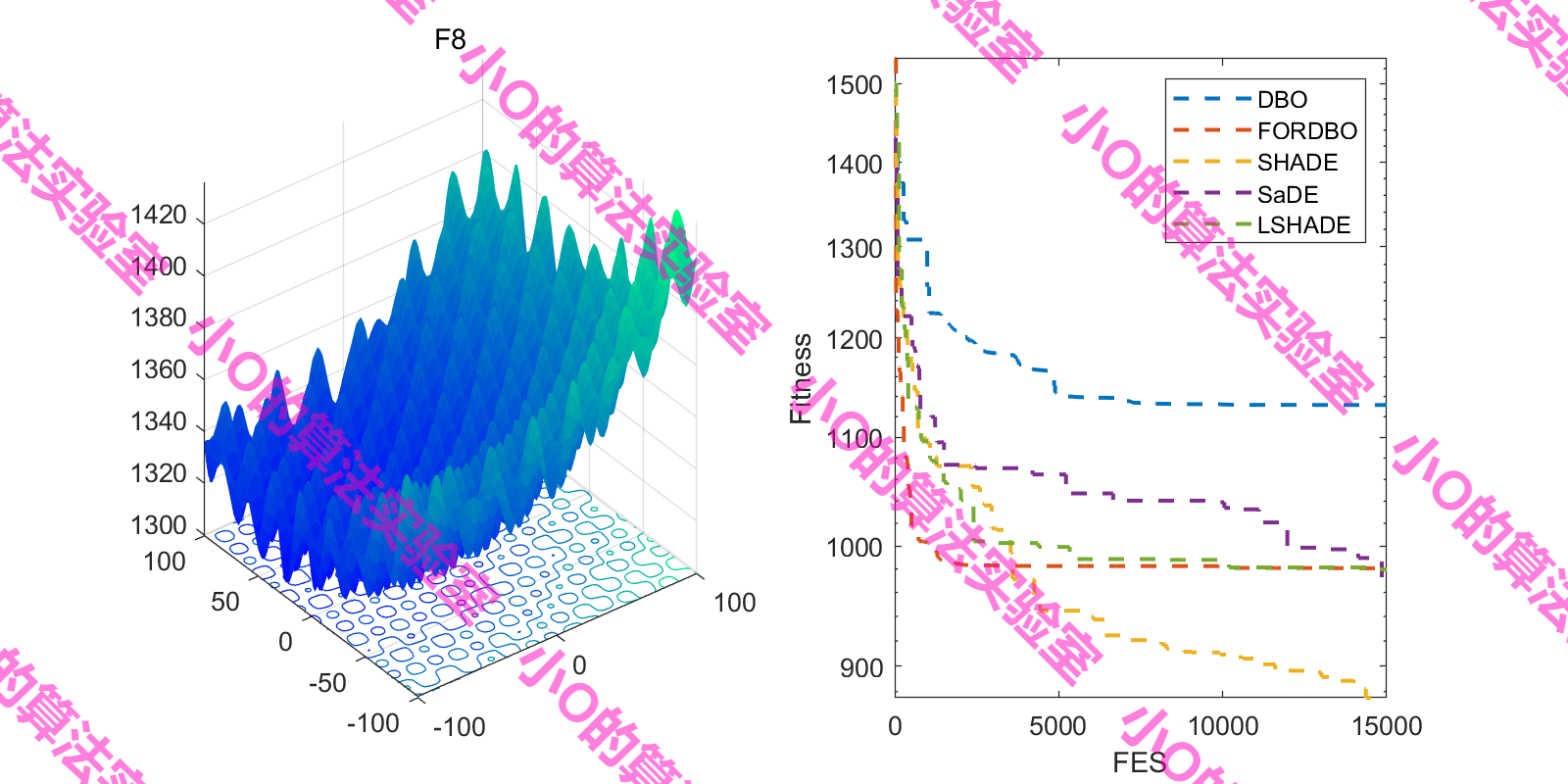
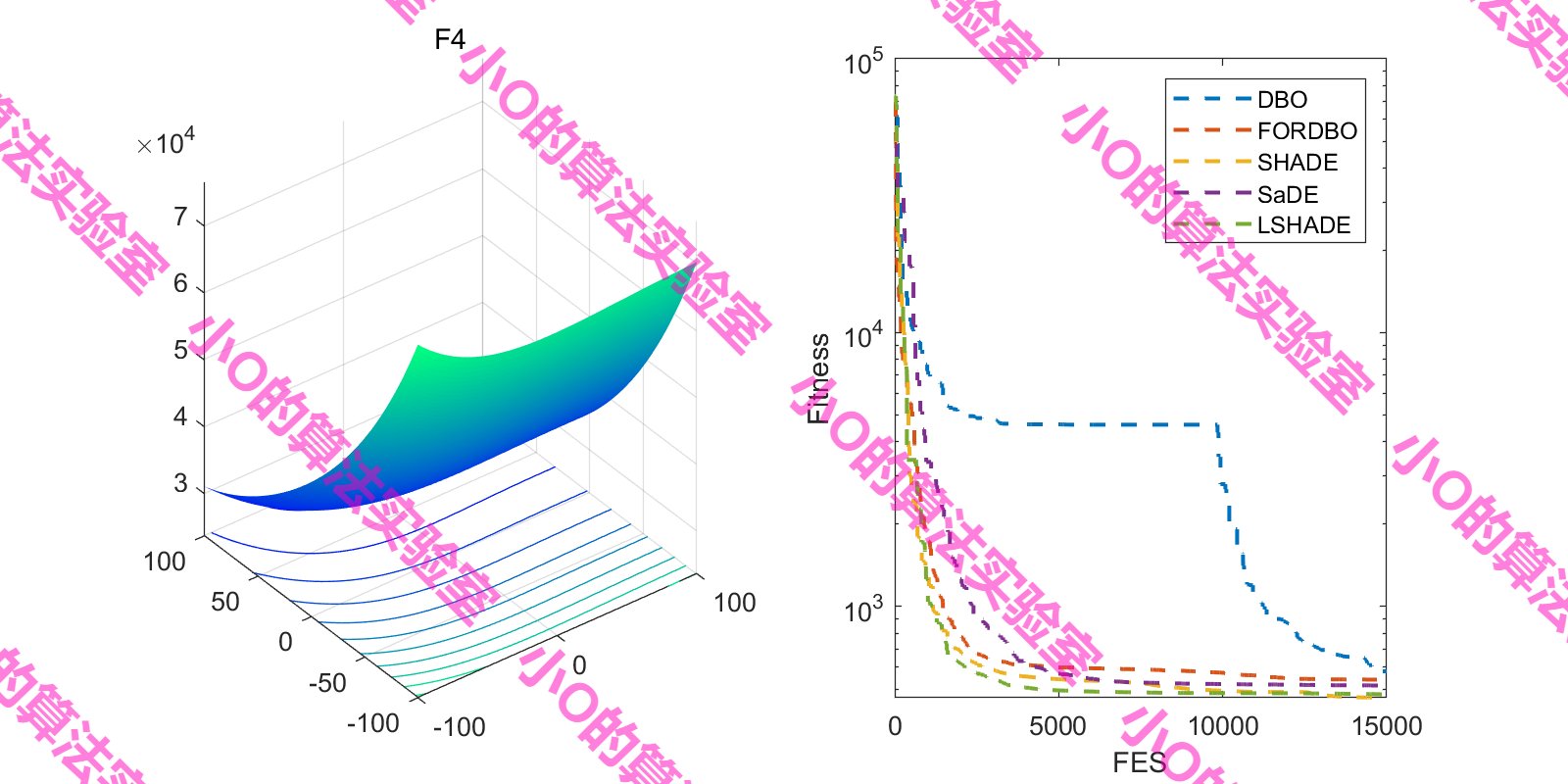
5.參考文獻

[1] Xia H, Ke Y, Liao R, et al. Fractional order dung beetle optimizer with reduction factor for global optimization and industrial engineering optimization problems[J]. Artificial Intelligence Review, 2025, 58(10): 308.

6.代碼獲取

xx

7.算法輔導·應用定制·讀者交流