目錄
1. 多重線性回歸
1.1 多元線性回歸
1.2 向量化(矢量化)
1.3?多元線性回歸的梯度下降算法
1.4?正規方程
2. 特征縮放
2.1?特征縮放
2.2?檢查梯度下降是否收斂
2.3 學習率的選擇
2.4?特征工程
2.5 多項式回歸
3. 邏輯回歸
3.1?Motivations
3.2?邏輯回歸
3.3 決策邊界
3.4?邏輯回歸的代價函數
4. 梯度下降的實現
5. 過擬合
5.1?過擬合問題
5.2 解決過擬合問題
5.3?正則化代價函數
5.4?正則化線性回歸
5.5?正則化邏輯回歸
本次學習筆記基于吳恩達機器學習視頻。
1. 多重線性回歸
1.1 多元線性回歸
矢量:

多元線性回歸:具有多個特征的線性回歸。
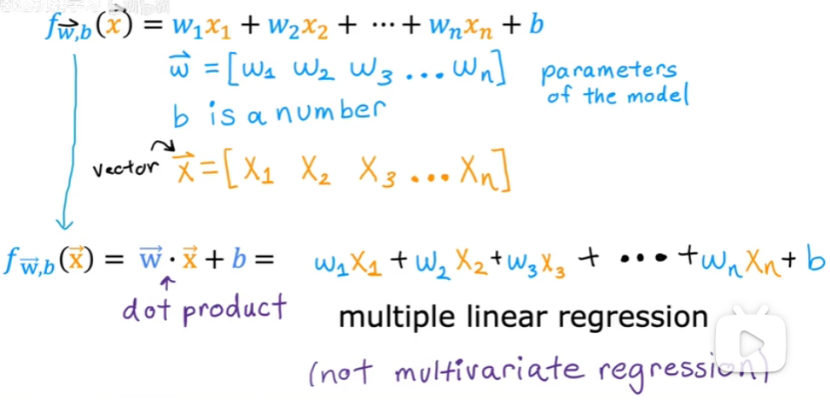
矢量化可以實現多元線性回歸。
1.2 向量化(矢量化)
(1)向量化:

向量化優點:使得代碼更加簡潔;代碼運行速度更快,如下圖:

(2)向量化運行更快的原因
For循環與向量化的對比,如下圖:
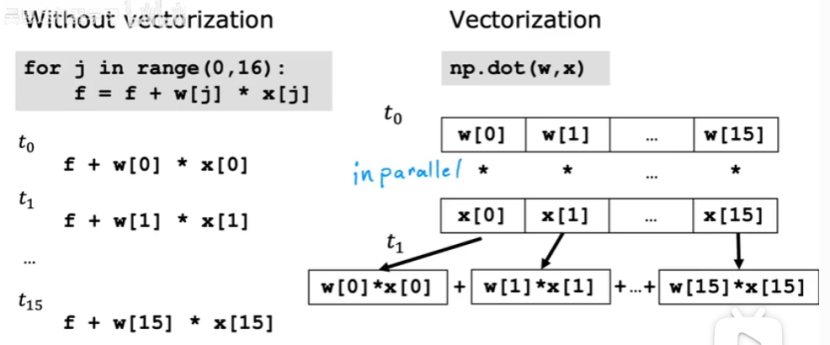
For循環是一步一步進行加法計算的。
向量化可以獲取全部數據進行計算后,再用固定的硬件將全部相加起來。
例子:向量化如何幫助實現多元線性回歸

向量化可以看成有16個數組,同時進行計算。
1.3?多元線性回歸的梯度下降算法
可以用向量化來實現多元線性回歸的梯度下降,如下圖:

當多個特征時,梯度下降與只有一個特征時會稍有不同,如下圖所示:
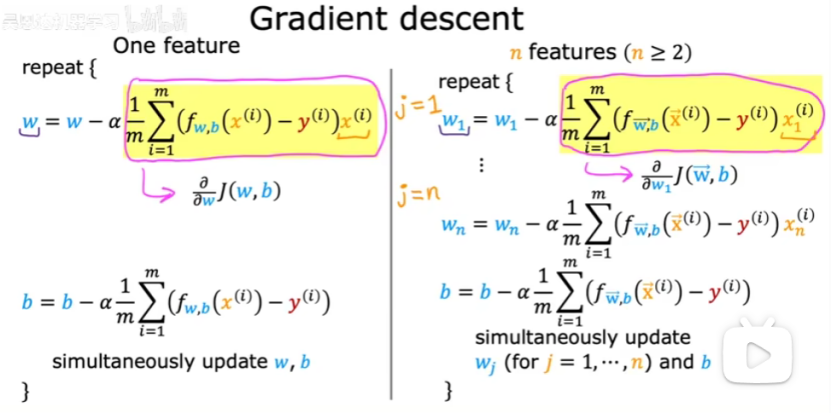
右邊就是多元梯度下降算法。
1.4?正規方程
正規方程:尋找線性回歸的w和b的替代方法的簡短旁注。(僅適合線性回歸,不需要迭代的梯度下降算法)
缺點:不能推廣到其他學習算法;特征數量n很大時,正規方程也相當慢。
2. 特征縮放
2.1?特征縮放
(1)特征縮放:使梯度下降更快。
當一個特征的取值范圍很大時,一個好的模型更可能會選擇一個相對較小的參數值。
當一個特征的取值范圍比較小時,一個好的模型更可能會選擇一個相對較大的參數值。
當你有不同特征取值范圍差異很大時,可能導致梯度下降運行緩慢。可以重新縮放不同的特征,使他們都在相似的范圍內取值,可以加快梯度下降的速度。
(2)如何實現特征縮放以處理取值范圍非常不同的特征,并且將他們縮放到具有可比的取值范圍?
①都除以最大值
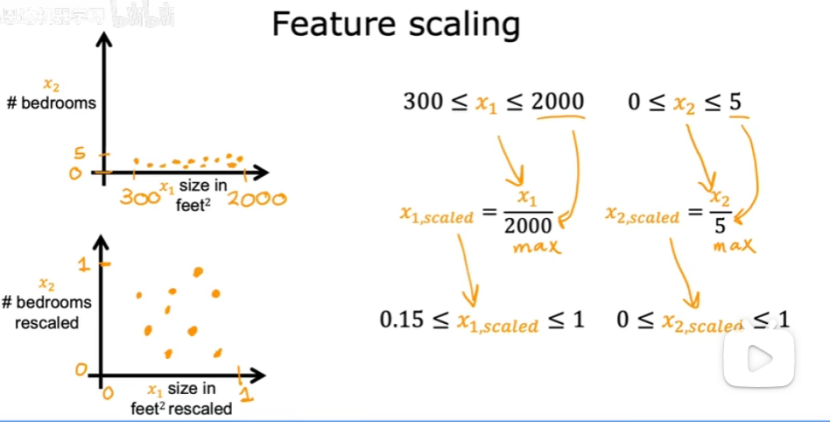
②均值歸一化(將所有數據都集中在0附近)。
找到訓練集上x1的均值,所有數減去均值,再除以差值。
找到訓練集上x2的均值,所有數減去均值,再除以差值。

③z-score歸一化(計算每個特征的均值和標準差)
每個x1減去均值再除以標準差。
每個x2減去均值再除以標準差。
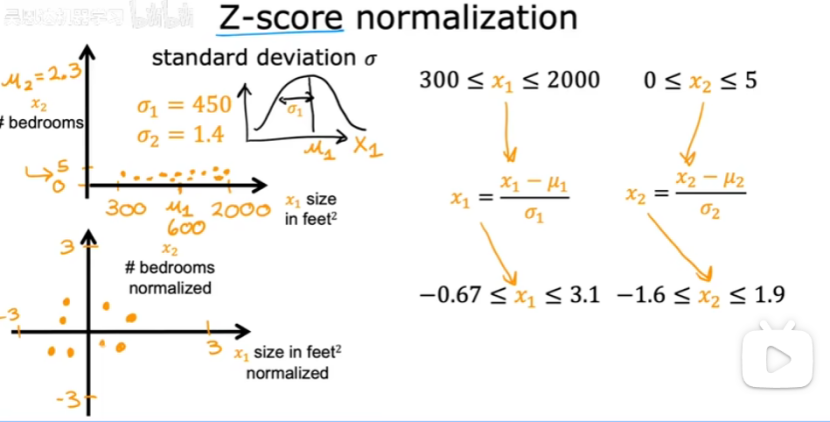
(3)特征的取值:

2.2?檢查梯度下降是否收斂
(1)學習曲線
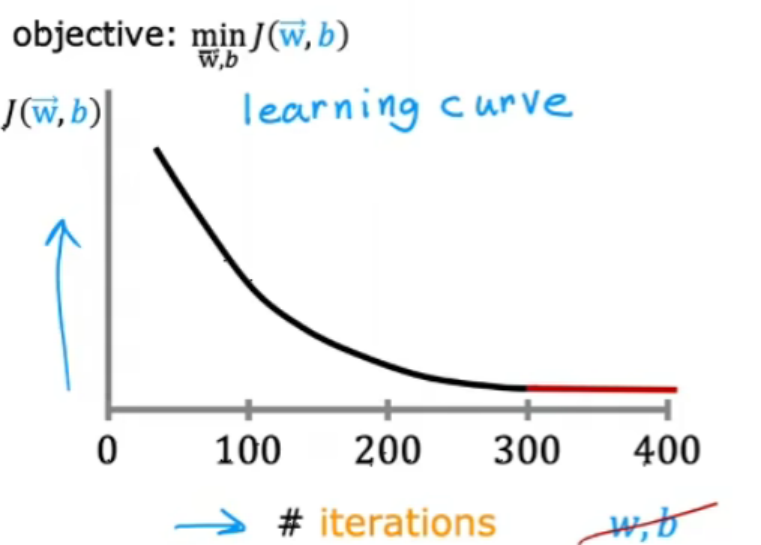
如果梯度下降正常工作,那么代價j應該在每次迭代后都減少。
如果j在一次迭代增加,那么意味著要么是a選擇不當(a太大)或者代碼中有錯誤。
當迭代到達300次時,代價j開始趨于平穩,不再有太大下降。到達400次時,梯度下降差不多已經收斂。
(2)檢查梯度下降是否收斂的方法
①觀察學習曲線,可以檢查梯度下降是否收斂。
梯度下降收斂所需的迭代次數在不同的情況下可能會有很大的差異。
②使用自動收斂測試
設置一個變量epsilon,表示一個小數。如果在一次迭代中,代價j的減少量小于這個epsilon,則很可能看到學習曲線的平坦部分,可以宣布收斂。
但是找到epsilon很困難,所以推薦查看學習曲率來檢查梯度下降是否收斂。
2.3 學習率的選擇
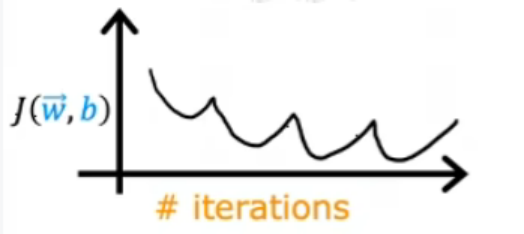
出現上圖的原因是可能代碼出現錯誤或者學習率太大。
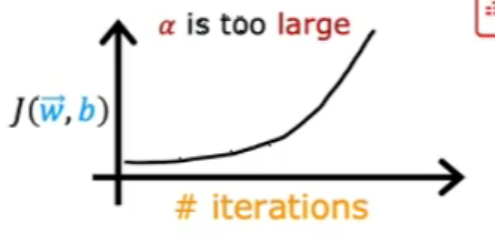
上圖是因為學習率太大導致的,可以減少學習率。(或者代碼的錯誤)
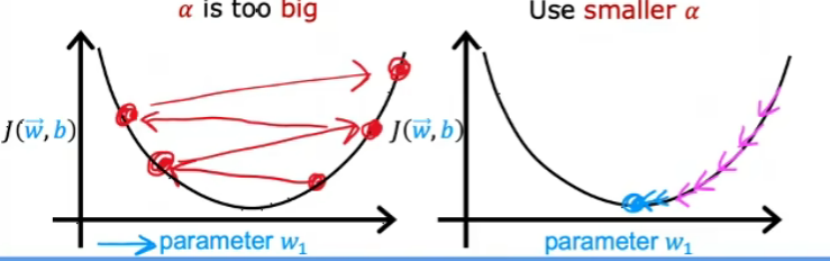
當學習率太大時,可能會出現上面左圖無法收斂的情況,可以減少學習率。
如果把學習率設置成一個很小很小的數值,但是學習曲線還是會出現上升的情況,表示代碼出現了錯誤。
但是學習率太小時,需要很多次迭代才可以達到收斂。
選擇學習率的技巧:
先選擇一個很小很小的數值,然后每一次擴大3倍,繼續嘗試,直到找到最合適的學習率可以使得學習曲線下降的比較快且平穩。
2.4?特征工程
使得多元線性回歸更加強大-->選擇自定義的特征
如何選擇或設計最合適的特征用于學習:可以利用對問題的知識或者直覺來設計新特征,通常通過轉化或組合問題的原始特征,以便讓學習算法更容易做出預測。
2.5 多項式回歸
多項式回歸可以擬合曲線,是將特征x提升到任何平方或者開根號。這樣的話更需要注意特征縮放。
3. 邏輯回歸
3.1?Motivations
二元分類:結果只有兩個可能的分類/類別
如何構建分類算法:可以看決策邊界(如下圖的垂直線)
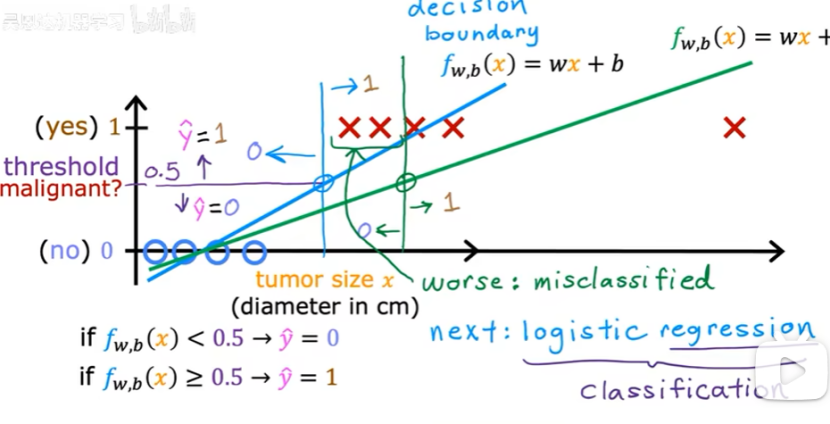
3.2?邏輯回歸
邏輯回歸:用于分類(用于解決輸出標簽y為0或1的二元分類問題)
Sigmoid函數:

f的結果表示等于1的概率。
3.3 決策邊界
f>=0.5時(z>=0時/wx+b>=0時),y=1;
f<0.5時(z<0時/wx+b<0時),y=0;
決策邊界:z=wx+b=0
例子:決策邊界為直線時
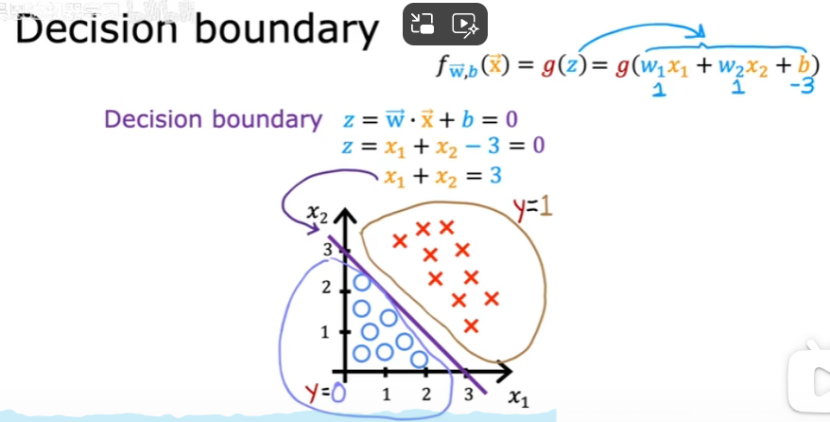
例子:決策邊界為曲線時

3.4?邏輯回歸的代價函數
為什么平方誤差成本函數不是邏輯回歸的理想成本函數?
因為梯度下降時會遇到很多局部最小值,如下圖:
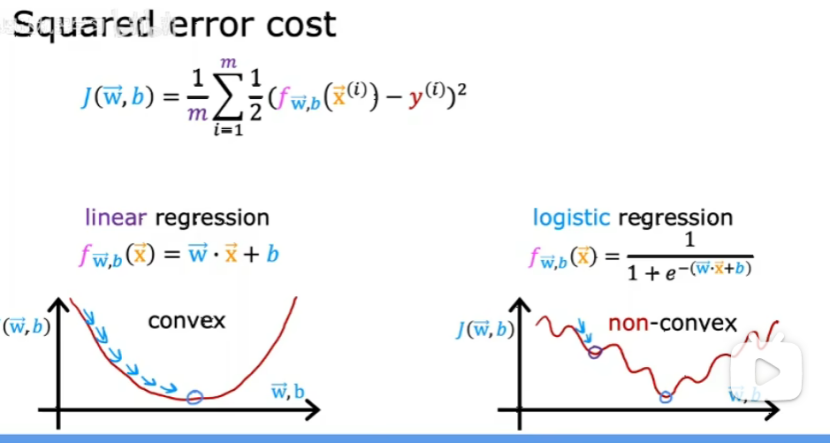
損失函數:
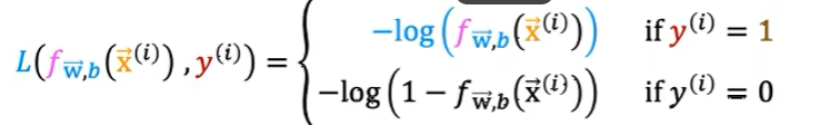
①Y=1時,預測值接近1時,損失最小,如下圖:
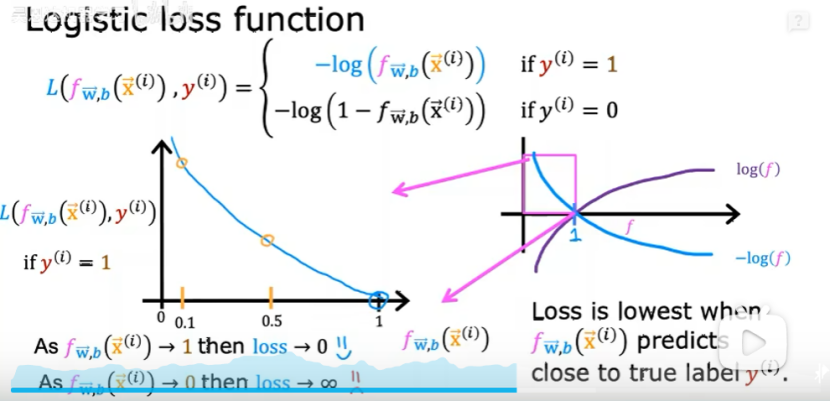
②Y=0時,預測值接近0時,損失最小,如下圖:
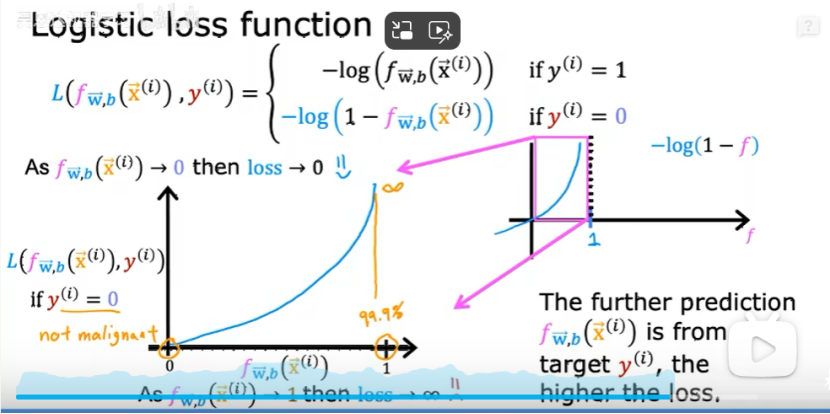
損失函數的簡化版公式如下:
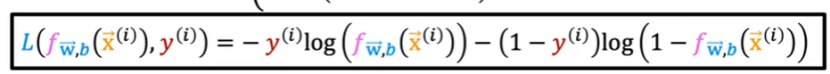
訓練邏輯回歸的代價函數如下:
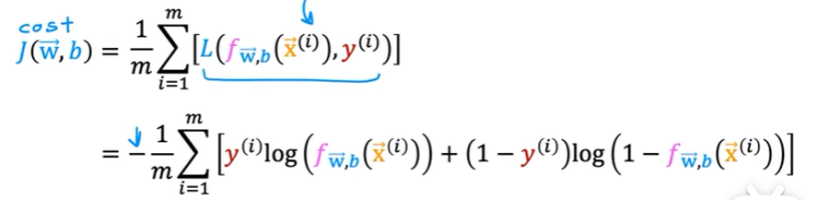
4. 梯度下降的實現
如何找到一個合適的w和b?

把右側帶入左側,得到下面:

上面與線性回歸的區別:函數f(x)的定義已經改變了,如下圖:

5. 過擬合
5.1?過擬合問題
泛化:對于全新的例子也能做出良好的預測。
下面是沒有過擬合也沒有欠擬合的情況:
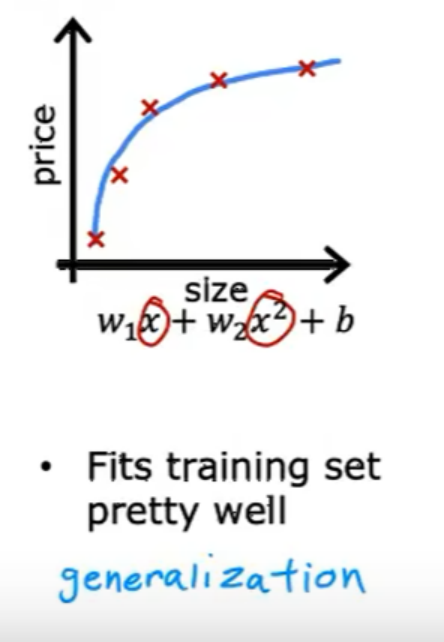
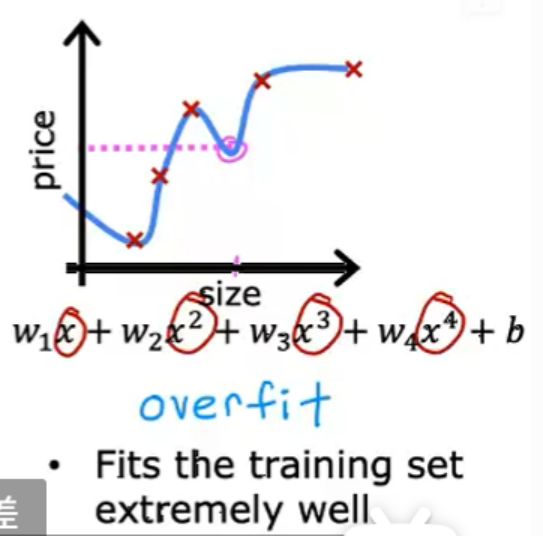
過擬合/算法有高方差:模型太復雜,導致在訓練集上表現很好,但在測試集上泛化能力差。如下圖情況:
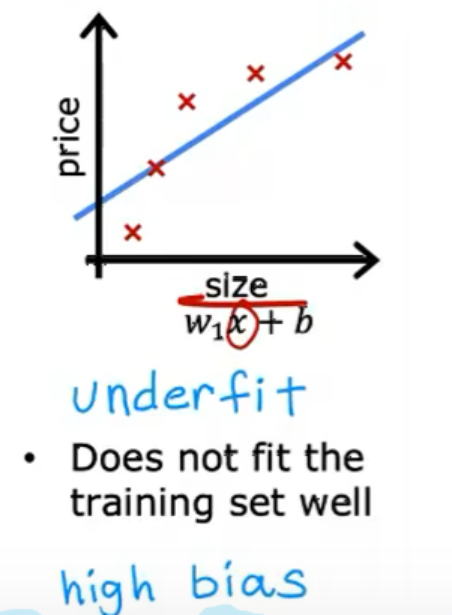
欠擬合:模型太過簡單,無法很好擬合訓練數據。如下圖情況:
5.2 解決過擬合問題
(1)收集足夠多的訓練數據,可以保證盡管是過擬合的模型,也可以表現很好。
(2)減少多項式的特征:進行特征選擇(選擇最重要的幾個特征集)
(3)正則化:更溫和的減少某些特征影響的方法,而不需要去除他們。(將特征的參數大小減小)
一般只正則化w1~wn,而不正則化b。
5.3?正則化代價函數
當特征的參數較小時,模型比較簡單,不容易產生過擬合的情況。
當不知道哪些參數是重要的時候,就懲罰所有特征參數;

如果正則率(![]() )=0,則表示沒有正則化
)=0,則表示沒有正則化
如果正則率特別大,f(x)約等于b;學習算法會擬合出一條水平直線,并出現欠擬合。
5.4?正則化線性回歸

帶入后如下:
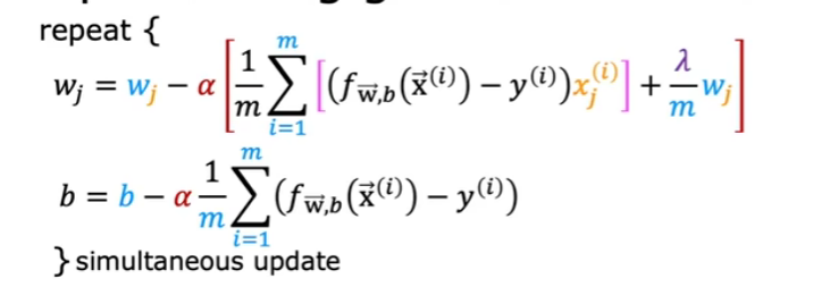
注意:只正則化w,不正則化b。
5.5?正則化邏輯回歸
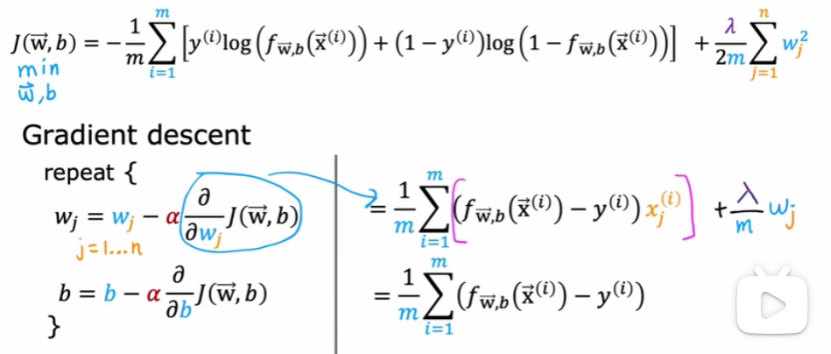

)

















