MADlib —— 基于 SQL 的數據挖掘解決方案（9）—

一、概率

1. 概率的定義

2. 概率質量函數與概率密度函數

3. 條件概率

4. 期望值

二、MADlib 的概率相關函數

1. 函數語法

2. 示例

（1）求標準正態分布下，1 的概率密度函數

（2）求標準正態分布下，1 的累積分布函數

（3）求標準正態分布下，概率為 0、0.25、0.5、0.75、1 的分位數值。

三、統計推論

1. 點估計

2. 中心極限定理

3. 區間估計

4. 假設檢驗

四、MADlib 的假設檢驗

1. 輸入的數據

2. 使用方法

五、MADlib 假設檢驗示例

1. 單樣本 T 檢驗

（1）建立檢驗假設，確定檢驗標準

（2）執行單樣本 T 檢驗

2. 帶參數兩樣本 T 檢樣

（1）建立檢驗假設，確定檢驗標準?

（2）執行帶參數兩樣本 T 檢樣

3. F-Test 檢驗

4. 擬合優度檢驗

（1）建立檢驗假設，確定檢驗標準

（2）執行擬合優度檢驗

5. 卡方獨立性檢驗

（1）建立檢驗假設，確定檢驗標準

（2）卡方獨立性檢驗

6. 方差分析

7. Kolmogorov-Smirnov 檢驗

（1）建立檢驗假設，確定檢驗標準

（2）執行 K-S 檢驗

8. Mann-Whitney 檢驗

9. Wilcoxon 符號秩檢驗

? ? ? ? 樣本是隨機變量，統計量作為樣本的函數自然也是隨機變量。當用它們去推斷總體時，有多大的可靠性與統計量的概率分布有關。本篇學習概率統計的基本知識，以及在此基礎上的統計推論。MADlib 提供了概率函數和統計推論兩個模塊，分別用于實現概率和假設檢驗相關的函數。

一、概率

1. 概率的定義

? ? ? ? 我們從隨機試驗開始討論。隨機試驗（random experiment）是測量其結果不確定的過程的試驗，所有可能結果的集合稱為樣本空間（sample space）Ω。例如，對于擲一個色子，Ω={1,2,3,4,5,6} 是樣本空間。事件（event）E?對應于這些結果的一個子集，即?E?Ω 。例如，E={2,4,6} 是擲一個色子時觀察到偶數點的事件。

? ? ? ? 概率?P?是定義在樣本空間 Ω 上的實數值的函數，滿足如下性質：

對于任意事件?E?Ω，0≤P(E)≤1。
P(Ω)=1。
對于任意不相交的事件集?，

? ? ? ? 事件?E?的概率記作?P(E)，是在可能無窮多次試驗中觀測到?E?的次數所占的比例。?

2. 概率質量函數與概率密度函數

? ? ? ? 在隨機試驗中，通常有一個我們想測量的量。例如，統計擲 50 次硬幣背面朝上的次數。因為這種量值依賴于隨機試驗的結果，所以這種感興趣的量稱為隨機變量（random variable）。隨機變量的值可能是離散的或連續的。

? ? ? ? 對于離散隨機變量?X，X?取特定值?x?的概率是?X(e)=x?的所有結果?e?的總概率。

P(X=x)=P(E={e|e∈Ω,X(e)=x})

? ? ? ? 離散隨機變量?X?的概率分布也稱作它的概率質量函數（probability mass function，pmf）。

? ? ? ? 例1，考慮隨機投一枚均勻硬幣 4 次的隨機試驗。該試驗有? 種可能的結果。設?X?是隨機變量，度量在試驗中觀測到背面的次數。X?的 5 個可能值是 0、1、2、3、4。X?的概率質量函數由下表給出。P(X=2)=6/16，因為在 4 次投擲中觀測到兩次背面的結果有 6 種。

X	0	1	2	3	4
P(X)	1/16	4/16	6/16	4/16	1/16

? ? ? ? 如果?X?是連續隨機變量，則?X?的值在?a?和?b?之間的概率為：

? ? ? ? 函數? 稱為累積分布函數（Cumulative Distribution Function，CDF），函數?f(x) 稱為概率密度函數（probability density function，pdf）。因為?f?是連續分布，所以?X?取特定值?x?的概率總是為 0。

? ? ? ? 表1 顯示了一些著名的離散和連續概率函數。概率（質量或密度）函數的概念可以推廣到多個隨機變量。例如，如果?X?和?Y?是隨機變量，則?p(X,Y) 表示聯合（joint）概率函數。如果P(X,Y)=P(X)×P(Y)，表示隨機變量?X?和?Y?是相互獨立的。兩個隨機變量是獨立的，意味著一個變量的值對另一個的值沒有影響。?

	概率函數	參數
高斯		μ,σ
伯努利		n,p
泊松		θ
指數		θ
Г		λ,α
卡方		k

表1 概率函數的例子（Γ(n+1)=nΓ(n) 并且 Γ(1)=1）

3. 條件概率

? ? ? ? 對于理解隨機變量之間的依賴性，條件概率（conditional probability）是另一個有用的概念。給定?X，變量?Y?的條件概率記作?P(Y|X)，定義為：

? ? ? ? 如果?X?和?Y?是獨立的，則?P(Y|X)=P(Y)。使用稱作 Bayes 定理的公式，條件概率?P(Y|X) 和?P(X|Y) 都可以用另一個表示。Bayes 定理由下式給出：?

? ? ? ? 如果? 是隨機變量?X?的所有可能的結果集，則上式的分母可以用下式表示：

? ? ? ? 上式稱作全概率律（law of total probability）。?

4. 期望值

? ? ? ? 隨機變量?X?的函數?g?的期望值（expected value）記作?E[g(X)]，是?g(X) 的加權平均值，其中權重由?X?的概率函數給出。如果?X?是離散隨機變量，則它的期望值可以用下式計算：

? ? ? ? 如果?X?是連續隨機變量，則：

? ? ? ? 其中?f(X) 是?X?的概率密度函數。本節的其余部分只考慮離散隨機變量的期望值，對應連續隨機變量的期望值可以通過用積分取代求和得到。

? ? ? ? 在概率論中，有一些特別有用的期望值。首先，如果?g(X)=X，則：

? ? ? ? 這個期望值對應于隨機變量?X?的均值（mean）。另一個有用的期望值是? 時的期望值。這個函數的期望值是：

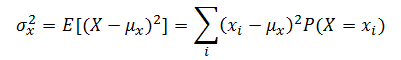
? ? ? ? 這個期望值對應于隨機變量?X?的方差（variance）。方差的平方根對應于隨機變量?X?的標準差（standard deviation）。

? ? ? ? 例2，考慮例1 中的隨機試驗。擲 4 次均勻的硬幣，期望看到背面朝上的平均次數為：

? ? ? ? 期望看到背面朝上次數的方差為：?

? ? ? ? 對于一對隨機變量，要計算的一個有用的期望是協方差（covariance）函數?Cov，它定義如下：?

? ? ? ? 注意，隨機變量?X?的方差等于?Cov(X,X)。函數的期望值還具有如下性質：

如果?α?是常量，則?E[α]=α。
E[αX]=αE[X]
E[αX + bY]=αE[X] + bE[Y]。

? ? ? ? 根據這些性質，方差和協方差公式可以寫成如下形式：

二、MADlib 的概率相關函數

? ? ? ? MADlib 的概率函數（prob）模塊提供了豐富的概率累積分布、密度/質量和分位函數。為了便于使用，所有累積分布和密度/質量函數（簡寫分別為 CDF 和 PDF/PMF）定義為處理包括無窮大在內的所有浮點數范圍內的數據。若輸入數據為 NULL 或者不是數字，函數產生的結果也是 NULL或非數字。無窮大輸入的運算結果將受限于浮點數的表示范圍。

? ? ? ? 分位函數（Quantile Function）是這樣一個累積概率分布函數?F，它接收概率參數?p∈[0,1]，如果存在一個唯一的?x，使得?F(x)=p，則返回?x。如果不存在這樣的?x，當?p<0.5，結果返回 sup{x∈D|F(x)<=p}，即所有滿足?F(x)<=p?的?x?的上界值；當?p>=0.5，結果為 inf{x∈D|F(x)>=p}，即所有滿足?F(x)>=p?的 x 的下界值。其中 D 表示分布的值域，這里包括連續的實數集 R，以及離散分布的非負整數集 N。

? ? ? ? 很明顯，上面的公式包括以下特殊情況。0 分位數總是數據集合中的最小值，1 分位數總是數據集合中的最大值。對于離散非負整數集合分布上的分位數 p∈[0,1]，由于 x∈N，因此公式演變為?F(x)<p<F(x+1)，就是說當?p<0.5 時，p?分位數返回滿足公式的?x，而當?p>=0.5 時，p?分位數返回滿足公式的?x+1。為了確保能得到分位數，作為一種特殊情況，p<F(0) 的?p?分位數為 0。

1. 函數語法

-- 累積分布函數
distribution_cdf(random variate[, parameter1 [, parameter2 [, parameter3] ] ])-- 概率密度/質量函數
distribution_{pdf|pmf}(random variate[, parameter1 [, parameter2 [, parameter3] ] ])-- 分位函數：
distribution_quantile(probability[, parameter1 [, parameter2 [, parameter3] ] ])

? ? ? ? 其中 distribution 指的是某種具體的分布，分布不同，參數也有所不同。MADlib 1.10.0 中提供的概率函數有 91 個，可按不同概率分布可分成以下類別。

伯努利分布

float8? bernoulli_cdf (float8 x, float8 sp)?
float8? bernoulli_pmf (int4 x, float8 sp)?
float8? bernoulli_quantile (float8 p, float8 sp)?

貝塔分布

float8? beta_cdf (float8 x, float8 alpha, float8 beta)?
float8? beta_pdf (float8 x, float8 alpha, float8 beta)?
float8? beta_quantile (float8 p, float8 alpha, float8 beta)?

二項分布

float8? binomial_cdf (float8 x, int4 n, float8 sp)?
float8? binomial_pmf (int4 x, int4 n, float8 sp)?
float8? binomial_quantile (float8 p, int4 n, float8 sp)?

柯西分布

float8? cauchy_cdf (float8 x, float8 location, float8 scale)?
float8? cauchy_pdf (float8 x, float8 location, float8 scale)?
float8? cauchy_quantile (float8 p, float8 location, float8 scale)?

卡方分布

float8? chi_squared_cdf (float8 x, float8 df)?
float8? chi_squared_pdf (float8 x, float8 df)?
float8? chi_squared_quantile (float8 p, float8 df)?

指數分布

float8? exponential_cdf (float8 x, float8 lambda)?
float8? exponential_pdf (float8 x, float8 lambda)?
float8? exponential_quantile (float8 p, float8 lambda)?

極值分布

float8? extreme_value_cdf (float8 x, float8 location, float8 scale)?
float8? extreme_value_pdf (float8 x, float8 location, float8 scale)?
float8? extreme_value_quantile (float8 p, float8 location, float8 scale)?

費舌爾分布

float8? fisher_f_cdf (float8 x, float8 df1, float8 df2)?
float8? fisher_f_pdf (float8 x, float8 df1, float8 df2)?
float8? fisher_f_quantile (float8 p, float8 df1, float8 df2)?

伽瑪分布

float8? gamma_cdf (float8 x, float8 shape, float8 scale)?
float8? gamma_pdf (float8 x, float8 shape, float8 scale)?
float8? gamma_quantile (float8 p, float8 shape, float8 scale)?

幾何分布

float8? geometric_cdf (float8 x, float8 sp)?
float8? geometric_pmf (int4 x, float8 sp)?
float8? geometric_quantile (float8 p, float8 sp)?

超幾何分布

float8? hypergeometric_cdf (float8 x, int4 r, int4 n, int4 N)?
float8? hypergeometric_pmf (int4 x, int4 r, int4 n, int4 N)?
float8? hypergeometric_quantile (float8 p, int4 r, int4 n, int4 N)?

逆伽瑪分布

float8? inverse_gamma_cdf (float8 x, float8 shape, float8 scale)?
float8? inverse_gamma_pdf (float8 x, float8 shape, float8 scale)?
float8? inverse_gamma_quantile (float8 p, float8 shape, float8 scale)?

Kolmogorov 分布

float8? kolmogorov_cdf (float8 x)?

拉普拉斯分布

float8? laplace_cdf (float8 x, float8 mean, float8 scale)?
float8? laplace_pdf (float8 x, float8 mean, float8 scale)?
float8? laplace_quantile (float8 p, float8 mean, float8 scale)?

邏輯斯諦分布

float8? logistic_cdf (float8 x, float8 mean, float8 scale)?
float8? logistic_pdf (float8 x, float8 mean, float8 scale)?
float8? logistic_quantile (float8 p, float8 mean, float8 scale)?

對數正態分布

float8? lognormal_cdf (float8 x, float8 location, float8 scale)?
float8? lognormal_pdf (float8 x, float8 location, float8 scale)?
float8? lognormal_quantile (float8 p, float8 location, float8 scale)?

負二項分布

float8? negative_binomial_cdf (float8 x, float8 r, float8 sp)?
float8? negative_binomial_pmf (int4 x, float8 r, float8 sp)?
float8? negative_binomial_quantile (float8 p, float8 r, float8 sp)?

非中心貝塔分布

float8? non_central_beta_cdf (float8 x, float8 alpha, float8 beta, float8 ncp)?
float8? non_central_beta_pdf (float8 x, float8 alpha, float8 beta, float8 ncp)?
float8? non_central_beta_quantile (float8 p, float8 alpha, float8 beta, float8 ncp)?

非中心卡方分布

float8? non_central_chi_squared_cdf (float8 x, float8 df, float8 ncp)?
float8? non_central_chi_squared_pdf (float8 x, float8 df, float8 ncp)?
float8? non_central_chi_squared_quantile (float8 p, float8 df, float8 ncp)?

非中心 F 分布

float8? non_central_f_cdf (float8 x, float8 df1, float8 df2, float8 ncp)?
float8? non_central_f_pdf (float8 x, float8 df1, float8 df2, float8 ncp)?
float8? non_central_f_quantile (float8 p, float8 df1, float8 df2, float8 ncp)?

非中心 T 分布

float8? non_central_t_cdf (float8 x, float8 df, float8 ncp)?
float8? non_central_t_pdf (float8 x, float8 df, float8 ncp)?
float8? non_central_t_quantile (float8 p, float8 df, float8 ncp)?

正態分布

float8? normal_cdf (float8 x, float8 mean=0, float8 sd=1)?
float8? normal_cdf (float8 x, float8 mean)?
float8? normal_cdf (float8 x)?
float8? normal_pdf (float8 x, float8 mean=0, float8 sd=1)?
float8? normal_pdf (float8 x, float8 mean)?
float8? normal_pdf (float8 x)?
float8? normal_quantile (float8 p, float8 mean=0, float8 sd=1)?
float8? normal_quantile (float8 p, float8 mean)?
float8? normal_quantile (float8 p)?

帕累托分布

float8? pareto_cdf (float8 x, float8 scale, float8 shape)?
float8? pareto_pdf (float8 x, float8 scale, float8 shape)?
float8? pareto_quantile (float8 p, float8 scale, float8 shape)?

泊松分布

float8? poisson_cdf (float8 x, float8 mean)?
float8? poisson_pmf (int4 x, float8 mean)?
float8? poisson_quantile (float8 p, float8 mean)?

瑞利分布

float8? rayleigh_cdf (float8 x, float8 scale)?
float8? rayleigh_pdf (float8 x, float8 scale)?
float8? rayleigh_quantile (float8 p, float8 scale)?

學生?t 分布

float8? students_t_cdf (float8 x, float8 df)?
float8? students_t_pdf (float8 x, float8 df)?
float8? students_t_quantile (float8 p, float8 df)?

三角分布

float8? triangular_cdf (float8 x, float8 lower, float8 mode, float8 upper)?
float8? triangular_pdf (float8 x, float8 lower, float8 mode, float8 upper)?
float8? triangular_quantile (float8 p, float8 lower, float8 mode, float8 upper)?

均勻分布

float8? uniform_cdf (float8 x, float8 lower, float8 upper)?
float8? uniform_pdf (float8 x, float8 lower, float8 upper)?
float8? uniform_quantile (float8 p, float8 lower, float8 upper)?

韋布爾分布

float8? weibull_cdf (float8 x, float8 shape, float8 scale)?
float8? weibull_pdf (float8 x, float8 shape, float8 scale)?
float8? weibull_quantile (float8 p, float8 shape, float8 scale)?

2. 示例

（1）求標準正態分布下，1 的概率密度函數

select madlib.normal_pdf(1,0,1), exp(-0.5)/sqrt(2*pi());

? ? ? ? 結果：

    normal_pdf     |     ?column?      
-------------------+-------------------0.241970724519143 | 0.241970724519143
(1 row)

（2）求標準正態分布下，1 的累積分布函數

select madlib.normal_cdf(1,0,1);

? ? ? ? 結果：

    normal_cdf     
-------------------0.841344746068543
(1 row)

? ? ? ? 正態分布的累積分布函數為：，上面的查詢是將 x=1、μ=0、σ=1 代入函數所求得的值。

（3）求標準正態分布下，概率為 0、0.25、0.5、0.75、1 的分位數值。

\x on
select madlib.normal_quantile(0, 0, 1),madlib.normal_quantile(0.25, 0, 1),madlib.normal_quantile(0.5, 0, 1),madlib.normal_quantile(0.75, 0, 1),madlib.normal_quantile(1, 0, 1);

? ? ? ? 結果：

-[ RECORD 1 ]---+-------------------
normal_quantile | -Infinity
normal_quantile | -0.674489750196082
normal_quantile | 0
normal_quantile | 0.674489750196082
normal_quantile | Infinity

三、統計推論

? ? ? ? 為了獲取關于總體的結論，從整個總體收集數據通常是不可行的。相反，我們必須基于從樣本數據收集的證據得到合理的結論。這種基于樣本數據獲取關于總體的可靠結論的過程稱作統計推論（statistical inference）。概括地說，統計推論是在對樣本數據進行描述的基礎上，對統計總體的未知數量特征做出以概率形式表述的推論。

1. 點估計

? ? ? ? 在統計學中，術語統計量（statistic）是指從樣本數據推導出的數值量。兩個最有用的統計量是樣本均值??和樣本方差??：

? ? ? ? 使用樣本統計量估計總體參數的過程稱為點估計（point estimation）。

? ? ? ? 例3，假設? 是從均值? 、方差? 的總體抽取的?N?個獨立同分布觀測的隨機樣本。令? 為樣本均值，則：

? ? ? ? 其中，，因為所有觀測都來自均值為? 的相同分布。這一結果表明樣本的均值?? 逼近總體均值?，特別是當?N?充分大時。用統計學的術語來說，樣本均值稱作總體均值的無偏（unbiased）估計。可以證明樣本均值的方差為：

? ? ? ? 由于總體的方差通常是未知的，因此通常用樣本方差? 替換? 來近似總體均值的方差。量? 稱為均值的標準誤差（standard error）。?

2. 中心極限定理

? ? ? ? 正態分布是最常用的概率分布，因為很多隨機現象都可以用這種分布建模。這是稱作中心極限定理（central limit theorem）的統計學原理的推論。

? ? ? ? 中心極限定理：考慮從均值為? 、方差為? 的概率分布抽取的、大小為?N?的隨機樣本。如果? 是樣本均值，則當樣本的規模增大時，的分布逼近均值為? 、方差為? 的正態分布。

? ? ? ? 無論隨機變量從何種分布提取，中心極限定理都成立。例如，假設我們從具有某個未知分布的數據集隨機地抽取?N?個獨立實例。令? 是一個隨機變量，它指示第?i?個實例是否被給定的分類器正確預測，即如果該實例被正確分類則?，否則?。樣本均值? 表示分類器的期望準確率。中心極限定理表明，盡管抽取實例的分布可能不是正態的，但是期望準確率（即樣本均值）往往是正態分布。

3. 區間估計

? ? ? ? 在估計總體的參數時，指出估計的可靠性是有用的。例如，假設我們對由隨機抽取的觀測估計總體均值? 感興趣。使用諸如樣本均值? 這樣的點估計可能并不充分，特別是當樣本的規模比較小時尤其如此。作為替代，給出一個以高概率包含總體均值的區間可能更有用。這種找到總體參數的區間的估計任務稱為區間估計（interval estimation）。令?θ?是需要估計的總體參數。如果：

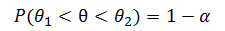
? ? ? ? 則 () 是?θ?在置信水平（confidence level）1-α?上的置信區間（confidence interval）。圖1 顯示了由均值為 0、方差為 1 的正態分布導出的參數的 95% 置信區間。正態分布下的陰影面積為 0.95。換言之，如果我們從該分布產生一個樣本，則被估計的參數落在 -2 和 +2 之間的可能性為 95%。?

圖1 參數的置信區間?

? ? ? ? 考慮一個隨機抽取的觀測序列?。我們想根據樣本均值? ，在 68% 置信區間估計總體均值? 。根據中心極限定理，當?N?充分大時，逼近均值為? 、方差為? 的正態分布。可以用如下方法把這種分布變換為標準正態分布（即均值為 0、方差為 1 的正態分布）：?

? ? ? ? 其中總體的標準差用樣本均值的標準誤差近似。查標準正態分布概率表得到?P(-1<Z<1)=0.68，該概率可以寫成：

? ? ? ? 或等價地改成：?

? ? ? ? 因此，的 68% 置信區間為? 。?

4. 假設檢驗

? ? ? ? 假設檢驗是數理統計中按照一定的假設條件由樣本推斷總體的一種方法，假設檢驗有時也稱為“顯著性檢驗（Test of statistical significant）”，是研究樣本與樣本之間、樣本與總體之間的誤差是由抽樣誤差引起還是本質誤差引起的統計推論方法。它的基本思想是在假設成立的條件下，根據某個統計方法（如T檢驗、卡方檢驗等）估計輸入數據的統計特性，根據統計特性和輸入數據的分布估計假設成立的概率大小，如果小于某一個預先設定的“顯著性水平（significant level）”則說明假設不成立，反之則說明假設成立。

? ? ? ? 假設檢驗所定義的假設稱為零假設，數學上一般寫成 H0。與 H0 對立的假設，即對立假設，也叫備擇假設。由于我們對于假設的判斷是基于概率統計所作出的，那么我們就很有可能（一定的概率）做出錯誤的判斷。錯誤分兩種，第一類錯誤為 H0 假設成立，但是我們卻認為它不成立，第二類錯誤是說 H0 不成立，但是我們卻認為它成立。一般而言，第一類錯誤更難為人所忍受，所以在判斷時，允許犯這種錯誤的可能性必須要極低——即犯第一類錯的事件應該是一個小概率事件。假設檢驗就是基于這種小概率原理，事先確定作為判斷的標準，即允許犯錯的小概率標準，這種小概率標準就是統計學上定義的“顯著性水平 α”，如果根據假設計算出來的概率小于這個顯著性水平，則拒絕原假設，反之，如果大于這個標準，則承認原假設。因此，一般把 1-α 稱為“置信區間”或者“接收區間”，小于 α 的區間稱為“拒絕區間”。

? ? ? ? 舉個例子來說明，一個人被控訴犯罪，陪審團根據現有的條件做出對這個人有罪還是無罪的判斷。事實上，陪審團就是進行一個假設檢驗。假設 H0：被告無罪；假設 H1：被告有罪。當然，陪審團現在還不知道哪個假設是成立的，他們必須根據控辯雙方的證詞做出判斷，判斷的結果只有兩種，一種是被告無罪釋放，一種是被告罪名成立。在判斷的過程中，陪審團可能犯的錯有兩種，一種是被告本來無罪被判成有罪，一種是被告有罪卻無罪釋放。從司法的角度來看，第一類的錯誤更嚴重，因此我們的司法系統要求構建的第一類錯誤的概率盡可能小。

? ? ? ? 假設檢驗的基本步驟如下：

提出檢驗假設又稱無效假設，符號是 H0；備擇假設的符號是 H1。H0 是樣本與總體或樣本與樣本間的差異是由抽樣誤差引起的，H1 是樣本與總體或樣本與樣本間存在本質差異。
選定可以允許的小概率標準，即假設 H0 成立卻錯誤判斷的可允許范圍 α；當檢驗假設為真，但被錯誤地拒絕的概率，記作 α，通常取 α=0.05 或 α=0.01。
選定統計方法，由樣本觀察值按相應的公式計算出統計量的大小，如 Z 值、T 值等。根據數據的類型和特點，可分別選用 F 檢驗，T 檢驗，秩和檢驗、卡方檢驗等。
根據統計量的大小及其分布確定檢驗假設成立的可能性 P 的大小并判斷結果。若 P>α，結論為按 α 所取水準不顯著，不拒絕 H0，即認為差別很可能是由于抽樣誤差造成的，在統計上不成立；如果 P≤α，結論為按所取 α 水準顯著，拒絕 H0，接受 H1，則認為此差別不大可能僅由抽樣誤差所致，很可能是實驗因素不同造成的，故在統計上成立。P 值的大小一般可通過查閱相應的界值表得到。

? ? ? ? 假設檢驗一般是參數、非參數檢驗都可以，但對于能使用參數檢驗的，首選參數檢驗，對不能滿足條件的才選用非參數檢驗。參數檢驗是在總體分布形式已知的情況下，對總體分布的參數如均值、方差等進行推斷的方法。但是，在數據分析過程中，由于種種原因，人們往往無法對總體分布形態作簡單假定，此時參數檢驗的方法就不再適用了。非參數檢驗正是一類基于這種考慮，在總體方差未知或知道甚少的情況下，利用樣本數據對總體分布形態等進行推斷的方法。由于非參數檢驗方法在推斷過程中不涉及有關總體分布的參數，因而得名“非參數檢驗”。?

四、MADlib 的假設檢驗

1. 輸入的數據

? ? ? ? 輸入的數據被假定為所有行存儲的都是規范化值。一般來說，期望如下形式的輸入數據。

單樣本檢驗輸入數據

{TABLE|VIEW} source (  ...  value DOUBLE PRECISION  ...  
)

?兩樣本檢驗輸入數據

{TABLE|VIEW} source (  ...  first BOOLEAN,  value DOUBLE PRECISION  ...  
)

? ? ? ? first 為真，表示數據來自第一個樣本，否則來自第二個樣本。

多樣本檢驗輸入數據

{TABLE|VIEW} source (  ...  group INTEGER,  value DOUBLE PRECISION  ...  
)

? ? ? ? group 標識數據所屬的樣本。

2. 使用方法

? ? ? ? 無論哪種輸入數據形式，所有的檢驗都是作為聚合函數實現的。非參數檢驗實現為有序聚合函數，因此需要包含 ORDER BY 子句。下面給出了最簡單的用法形式。

（1）運行參數單樣本檢驗

select test(value) from source，其中 test 可以是下面兩個函數之一：

t_test_one（單樣本 t 檢驗）
chi2_gof_test（卡方擬合優度檢驗）

（2）運行參數兩樣本/多樣本檢驗

select test(first/group, value) from source，其中 test 可以是下面函數之一：

f_test（F 檢驗）
t_test_two_pooled（等方差兩樣本 t 檢驗）
t_test_two_unpooled（韋爾奇 t 檢驗）
one_way_anova（多樣本單向方差分析）

（3）運行非參數兩樣本/多樣本檢驗

select test(first/group, value order by value) from source，其中 test 可以是下面函數之一：

ks_test（Kolmogorov-Smirnov 檢驗）
mw_test（Mann-Whitney 檢驗）
wsr_test (多樣本 Wilcoxon 符號秩檢驗)

五、MADlib 假設檢驗示例

1. 單樣本 T 檢驗

? ? ? ? 問題1：

? ? ? ? 正常人的脈搏平均數為 72次/分。現測得 15 名患者的脈搏：71、55、76、68、72、69、56、70、79、67、58、77、63、66、78。試問這 15 名患者的脈搏與正常人的脈搏是否有差異？假設脈搏數據符合正態分布。

? ? ? ? 該問題中只提供了一組樣本，因此采用單樣本 T 檢驗。

（1）建立檢驗假設，確定檢驗標準

? ? ? ? H0：這 15 名患者的脈搏與正常人的脈搏無顯著差異

? ? ? ? H1：這 15 名患者的脈搏與正常人的脈搏有顯著差異

? ? ? ? ɑ=0.05

? ? ? ? 一般來說，我們將一個假設放在 H0 上，是因為：1、我們對這個論述“感興趣”；2、方便構建檢驗統計量及確定相應的分布。選擇 H0、H1 的思考邏輯是：為了檢驗 H0 是否正確，先假定它正確。如果樣本的觀測值得出一個與 H0 應有的結果完全矛盾的結果，我們就“不能接受（拒絕）H0”，轉而接受 H1 的假設。出于以上的情況。H0，H1 是不對等的，不能隨意交換。通常情況下 H0 要取那個在實踐中受到保護、不證自明、要有足夠的證據才能否定它的等等諸如此類的命題。實際應用中我們常把相等的、無差別的、等號成立的結論作為 H0，將待證明的、不相等的、有差別的命題作為 H1。所以在具體統計中的參數檢驗，H0 表示相等，H1 則是大于、小于或者不相等。

（2）執行單樣本 T 檢驗

-- 建立輸入表，生成數據  
drop table if exists t1;  
create table t1 (a int);  
insert into t1 values   
(71),(55),(76),(68),(72),(69),(56),  
(70),(79),(67),(58),(77),(63),(66),(78);  -- 執行單樣本T檢驗  
select (madlib.t_test_one(a - 72)).* from t1;

? ? ? ? 結果：

     statistic     | df | p_value_one_sided | p_value_two_sided  
-------------------+----+-------------------+---------------------1.83625033332174 | 14 | 0.956177748242533 | 0.0876445035149334
(1 row)

? ? ? ? 從執行結果可知，p_value=0.088，按 ɑ=0.05 顯著性水平，p>ɑ，不拒絕 H0，差異無統計學意義。說明這 15 名患者的脈搏與正常人的脈搏差異不顯著。

? ? ? ? madlib.t_test_one 函數輸出四個字段：statistic 是統計量，df 表示自由度，p_value_one_sided 表示單尾 P 值，p_value_two_sided 表示雙尾 P 值。其中統計量的計算公式為：(樣本均值 - 標準值)/(樣本標準差/樣本數量的平方個)。可以執行以下查詢驗證函數輸出的統計值：

dm=# select (avg(a)-72)/(madlib.array_stddev(array_agg(a))/sqrt(count(*))) 
dm-#   from t1;?column?      
--------------------1.83625033332176
(1 row)

? ? ? ? 自由度為：樣本數量 - 1 = 15 - 1 = 14

2. 帶參數兩樣本 T 檢樣

? ? ? ? 問題2：

? ? ? ? 從問題1 的 15 名患者脈搏數據隨機抽樣兩組假設的樣本，判斷兩個整體數據有無顯著性差異。

（1）建立檢驗假設，確定檢驗標準?

? ? ? ? H0：無顯著差異

? ? ? ? H1：有顯著差異

? ? ? ? ɑ=0.05

（2）執行帶參數兩樣本 T 檢樣

-- 建立輸入表，生成數據  
drop table if exists t2;  
create table t2 as   
select * from (select true is_sample1,a from t1 order by random() limit 10) t1   
union all  
select * from (select false is_sample1,a from t1 order by random() limit 10) t2;

? ? ? ? 假設總體方差相等。?

select (madlib.t_test_two_pooled(is_sample1, a)).* from t2;

? ? ? ? 結果：

     statistic     | df | p_value_one_sided | p_value_two_sided 
-------------------+----+-------------------+-------------------0.267261241912424 | 18 | 0.396153078874935 | 0.792306157749869
(1 row)

? ? ? ? 假設總體方差不等。

select (madlib.t_test_two_unpooled(is_sample1, a)).* from t2;

? ? ? ? 結果：

     statistic     |        df        | p_value_one_sided | p_value_two_sided 
-------------------+------------------+-------------------+-------------------0.267261241912424 | 17.9934717562789 | 0.396153625447375 | 0.792307250894749
(1 row)

? ? ? ? 從執行結果可知，p_value=0.79，按 ɑ=0.05 顯著性水平，p>ɑ，不拒絕 H0，差異無統計學意義。說明兩組數據無顯著差異。

3. F-Test 檢驗

? ? ? ? F 檢驗又叫方差齊性檢驗。在兩樣本 T 檢驗中要用到 F 檢驗。從兩研究總體中隨機抽取樣本，要對這兩個樣本進行比較的時候，首先要判斷兩總體方差是否相同，即方差齊性。若兩總體方差相等，則直接用 T 檢驗，若不等，可采用 T' 檢驗或變量變換或秩和檢驗等方法。其中要判斷兩總體方差是否相等，就可以用 F 檢驗。

? ? ? ? 問題3：

? ? ? ? 對問題2 生成的兩組數據執行 F-Test 檢驗，判斷兩組整體數據方差是否相等。

select (madlib.f_test(is_sample1, a)).* from t2;

? ? ? ? 結果：

     statistic     | df1 | df2 | p_value_one_sided | p_value_two_sided 
-------------------+-----+-----+-------------------+-------------------0.962616822429907 |   9 |   9 | 0.522164040341636 | 0.955671919316729
(1 row)

? ? ? ? p_value=0.96，按 ɑ=0.05 顯著性水平，p>ɑ，說明兩組數據方差無顯著差異。

4. 擬合優度檢驗

? ? ? ? 擬合優度檢驗是用卡方統計量進行統計顯著性檢驗的重要內容之一。它依據總體分布狀況，計算出分類變量中各類別的期望頻數，與分布的觀察頻數進行對比，判斷期望頻數與觀察頻數是否有顯著差異，從而達到從分類變量進行分析的目的。

? ? ? ? 問題4：

? ? ? ? 交通部門統計事故與星期的關系得到：

? ? ? ? 星期：一? 二? 三? 四? 五? 六? 日?

? ? ? ? 次數：36? 23 29? 31 34? 60?25?

? ? ? ? 問每天事故發生的可能性是否相同？

（1）建立檢驗假設，確定檢驗標準

? ? ? ? H0：每天事故發生的可能性相同

? ? ? ? H1：每天事故發生的可能性不同

? ? ? ? ɑ=0.05

（2）執行擬合優度檢驗

-- 建立表，生成數據  
drop table if exists t1;  
create table t1 (a int);  
insert into t1 values (36),(23),(29),(31),(34),(60),(25);  -- 執行擬合優度檢驗  
select (madlib.chi2_gof_test(a, avg_a)).* from t1,(select avg(a) avg_a from t1) t;

? ? ? ? 結果：

    statistic     |      p_value       | df |       phi        | contingency_coef  
------------------+--------------------+----+------------------+-------------------26.9411764705882 | 0.0001485283360829 |  6 | 1.96182045452644 | 0.890932563042277
(1 row)

? ? ? ? p_value=0.00015，按 ɑ=0.05 顯著性水平，p<ɑ，拒絕 H0，差異具有統計學意義，說明事故發生的可能性不同，的確與星期幾有關。

5. 卡方獨立性檢驗

? ? ? ? MAdlib 的卡方獨立性檢驗利用擬合優度檢驗函數實現。對于輸入矩陣的的每個元素 (i,j)，它的期望值為 sum(第 i 行) * sum(第 j 列)。例如，元素 (2,1) 的期望值為 sum(第 2 行) * sum(第 1 列)。

? ? ? ? 卡方獨立性檢驗就是統計樣本的實際觀測值與理論推論值之間的偏離程度，它決定了卡方值的大小。卡方值越大，越不符合；卡方值越小，偏差越小，越趨于符合，若兩個值完全相等時，卡方值就為 0，表明理論值完全符合。

? ? ? ? 問題5：

? ? ? ? 某醫療機構為了解患肺癌與吸煙是否有關，進行了一次抽樣調查，共調查了 9965 個成年人，其中吸煙者 2148 人，不吸煙者 7817 人。調查結果是：吸煙的 2148 人中 49 人患肺癌，2099 人不患肺癌；不吸煙的 7817 人中 42 人患肺癌，7775 人不患肺癌。根據這些數據能否斷定：患肺癌與吸煙有關？

（1）建立檢驗假設，確定檢驗標準

? ? ? ? H0：患肺癌與吸煙無關

? ? ? ? H1：患肺癌與吸煙有關

? ? ? ? ɑ=0.05

（2）卡方獨立性檢驗

-- 建立表，生成數據  
drop table if exists t1;  
create table t1 (x int, y int, observed int);  
insert into t1 values   
(1,1,7775),(1,2,42),(2,1,2099),(2,2,49);  -- 執行卡方獨立性檢驗  
select (madlib.chi2_gof_test(observed, expected, deg_freedom)).*  from (-- 計算期望值和自由度  select observed,  sum(observed) over (partition by x)::double precision *  sum(observed) over (partition by y) as expected  from t1) t1,   (select (count(distinct x) - 1) * (count(distinct y) - 1) as deg_freedom  from t1) t2;

? ? ? ? 結果：

    statistic     |       p_value        | df |       phi        | contingency_coef  
------------------+----------------------+----+------------------+-------------------56.6318791461147 | 5.25529137942519e-14 |  1 | 3.76270777320385 | 0.966451294384498
(1 row)

? ? ? ? p_value 比 ɑ 小得多，因此拒絕 H0，患肺癌與吸煙有關。

6. 方差分析

? ? ? ? 一個復雜的事物，其中往往有許多因素互相制約又互相依存。方差分析的目的是通過數據分析找出對該事物有顯著影響的因素，各因素之間的交互作用，以及顯著影響因素的最佳水平等。方差分析是在可比較的數組中，把數據間的總的“變差”按各指定的變差來源進行分解的一種技術。對變差的度量，采用離差平方和。方差分析方法就是從總離差平方和分解出可追溯到指定來源的部分離差平方和，這是一個很重要的思想。

? ? ? ? 問題6：

? ? ? ? 設有三個車間以不同工藝生產同一種產品，為考察不同工藝對產品產量的影響，現對每個車間記錄 5 天的日產量，如下所示，三個車間的日產量是否有顯著差異？

序號 A1 A2 A3??

1? ? ? 44 50 47?

2? ? ? 45 51 44?

3? ? ? 47 53 44?

4? ? ? 48 55 50?

5? ? ? 46 51 45?

-- 建立表，生成數據  
drop table if exists t1;  
create table t1 (x int, observed int);  
insert into t1 values   
(1,44),(2,50),(3,47),  
(1,45),(2,51),(3,44),  
(1,47),(2,53),(3,44),  
(1,48),(2,55),(3,50),  
(1,46),(2,51),(3,45);  -- 執行方差分析
\x on  
select (madlib.one_way_anova(x, observed)).* from t1;

? ? ? ? 結果：

-[ RECORD 1 ]--------+---------------------
sum_squares_between  | 120
sum_squares_within   | 52
df_between           | 2
df_within            | 12
mean_squares_between | 60
mean_squares_within  | 4.33333333333333
statistic            | 13.8461538461538
p_value              | 0.000763570920161526

? ? ? ? 由輸出的結果可以得到如下方差分析表：

差異來源	離差平方和	自由度	平均平方和	F
組間	120	2	60	13.85
組內	52	12	4.33
總計	172	14

? ? ? ? p_value 遠小于 0.05，故得出結論是三個車間的日產量有顯著差異。

7. Kolmogorov-Smirnov 檢驗

? ? ? ? K-S 檢驗以兩位數學家 Kolmogorov 和 Smirnov 的名字命名，它是一個擬合優度檢驗，研究樣本觀察值的分布和設定的理論分布是否吻合，通過對兩個分布差異的分析確定是否有理由認為樣本的觀察結果來自所假定的理論分布總體。K-S 檢驗的基本思路是：先將順序分類資料數據的理論累積頻率分布與觀測的經驗累積頻率分布加以比較，求出它們最大的偏離值，然后在給定的顯著性水平上檢驗這種偏離值是否是偶然出現的。

? ? ? ? 從 madlib.ks_test 函數的入參定義可以看出，MADlib 的 K-S 檢驗只支持兩樣本。

dm=# \df+ madlib.ks_test  
List of functions  
-[ RECORD 1 ]-------+------------------------------------------  
Schema              | madlib  
Name                | ks_test  
Result data type    | madlib.ks_test_result  
Argument data types | boolean, double precision, bigint, bigint  
Type                | agg  
Data access         | no sql  
Volatility          | immutable  
Owner               | gpadmin  
Language            | internal  
Source code         | aggregate_dummy  
Description         |   
————————————————

? ? ? ? 問題7：

? ? ? ? 為了研究兩家電信運營商套餐在目標市場的年齡維度上的分布是否相同，該電信運營公司開展了一個社會調查活動。兩種通信套餐的用戶年齡數據如下：

? ? ? ? 套餐1：18，18，25，22，24，23，26?

? ? ? ? 套餐2：22，48，51，34，42，26，44，31，38?

（1）建立檢驗假設，確定檢驗標準

??????? H0：兩種套餐的目標市場年齡分布不存在顯著差異

??????? H1：兩種套餐的目標市場年齡分布存在顯著差異

??????? ɑ=0.05

（2）執行 K-S 檢驗

-- 建立表，生成數據  
drop table if exists t1;  
create table t1 (first boolean, observed int);  
insert into t1 values   
(true,18),(true,18),(true,25),(true,22),(true,24),(true,23),(true,26),  
(false,22),(false,48),(false,51),(false,34),(false,42),(false,26),(false,44),(false,31),(false,38);  -- 執行K-S檢驗  
select (madlib.ks_test(first, observed,  (select count(observed) from t1 where first),  (select count(observed) from t1 where not first)  order by observed)).*  from t1;

? ? ? ? 結果：

     statistic     |   k_statistic   |       p_value       
-------------------+-----------------+---------------------0.777777777777778 | 1.6798042120791 | 0.00708102048291268
(1 row)

? ? ? ? 相應的 P 值為 0.007，在 5% 的顯著性水平上，P 值足夠小，因此拒絕原假設，表明兩種套餐的目標市場年齡分布存在顯著差異。

8. Mann-Whitney 檢驗

? ? ? ? Mann-Whitney 檢驗假設兩個樣本分別來自除了總體均值以外完全相同的兩個總體，目的是檢驗這兩個總體的均值是否有顯著的差別。

? ? ? ? 問題8：

? ? ? ? 一種產品有兩種不同的工藝生產方法，它們的使用壽命數據如下：

? ? ? ? 工藝甲：661，669，675，679，682，692，693?

? ? ? ? 工藝乙：646，649，650，651，652，662，663，672?

? ? ? ? 它們的使用壽命分布是否相同？

-- 建立表，生成數據  
drop table if exists t1;  
create table t1 (first boolean, observed int);  
insert into t1 values   
(true,661),(true,669),(true,675),(true,679),(true,682),(true,692),(true,693),  
(false,646),(false,649),(false,650),(false,651),(false,652),(false,662),(false,663),(false,672);  -- 執行Mann-Whitney檢驗  
select (madlib.mw_test(first, observed order by observed)).* from t1;

? ? ? ? 結果：

     statistic     | u_statistic | p_value_one_sided |  p_value_two_sided  
-------------------+-------------+-------------------+----------------------2.77746029931765 |           4 | 0.997260723378726 | 0.00547855324254737
(1 row)

? ? ? ? P 值小于 0.05，表明兩種工藝生產方法的使用壽命分布是不相同的。

9. Wilcoxon 符號秩檢驗

? ? ? ? 在 Wilcoxon 符號秩檢驗中，它把觀測值和零假設的中心位置之差的絕對值的秩分別按照不同的符號相加作為其檢驗統計量。它適用于T檢驗中的成對比較，但并不要求成對數據之差服從正態分布，只要求對稱分布即可。檢驗成對觀測數據之差是否來自均值為0的總體（產生數據的總體是否具有相同的均值）。

? ? ? ? 問題9：

? ? ? ? 為了研究某放松方法（如聽音樂）對于入睡時間的影響，選擇了 10 名志愿者，分別記錄未進行放松時的入睡時間及放松后的入睡時間（單位為分鐘），得到如下數據：

? ? ? ? 放松前：21，12，12，23，19，13，20，17，14，19?

? ? ? ? 放松后：12，11， 8， 9，10，15，16，17，10，16?

? ? ? ? 請問該放松方法對入睡時間有無影響？

? ? ? ? 本例可以采用配對樣本 T 檢驗，但由于樣本量少，數據可能不符合正太分布，所以考慮用非參數檢驗。

-- 建立表，生成數據  
drop table if exists t1;  
create table t1 (x double precision, y double precision);  
insert into t1 values   
(21,12),(12,11),(12,8),(23,9),(19,10),(13,15),(20,16),(17,17),(14,10),(19,16);  -- 執行Wilcoxon符號秩檢驗  
\x on  
select (madlib.wsr_test(x - y order by abs(x - y))).* from t1;

? ? ? ? 結果：

-[ RECORD 1 ]-----+--------------------  
statistic         | 2  
rank_sum_pos      | 43  
rank_sum_neg      | 2  
num               | 9  
z_statistic       | 2.43935288096579  
p_value_one_sided | 0.00735679621140208  
p_value_two_sided | 0.0147135924228042

? ? ? ? P=0.015<0.05，拒絕原假設，認為放松前后有統計學差異。