
paxos算法_初步感知
Paxos算法保證一致性主要通過以下幾個關鍵步驟和機制:
?
準備階段
?
- 提議者向所有接受者發送準備請求,請求中包含一個唯一的編號。
?
- 接受者收到請求后,會檢查編號,如果編號比它之前見過的都大,就會承諾不再接受編號更小的提議,并回復提議者,告知自己已接受過的最大編號的提議。
?
提議階段
?
- 提議者收到多數接受者的回復后,根據回復內容來確定提議的值。如果有接受者在回復中包含了已接受的提議值,提議者就從中選擇編號最大的提議值作為自己要提議的值;如果沒有,提議者就自己選擇一個值。然后,提議者將選定的值和編號一起作為提議發送給接受者。
?
- 接受者收到提議后,只有在之前沒有承諾過不接受該提議,并且提議的編號不小于它之前見過的最大編號時,才會接受該提議。
?
學習階段
?
- 一旦有多數接受者接受了某個提議,這個提議就被認為是達成了一致。此時,系統中的其他節點可以通過學習這個已達成一致的提議來更新自己的狀態,從而保證整個系統的一致性。
?
通過這一系列的步驟,Paxos算法能夠在分布式系統中,即使存在節點故障、消息丟失等情況,也能保證最終達成一致的狀態,確保數據的一致性和正確性
舉個栗子🌰
假設你和一群朋友打算一起去看電影,但是對于看哪部電影大家有不同的想法,這時就可以用類似Paxos算法的方式來達成一致:
?
準備階段
?
- 你主動站出來成為“提議者”,你先給每個朋友發消息說:“我準備提議看一部電影,我現在的提議編號是1(這個編號是唯一且不斷遞增的),你們之前有沒有收到過其他人的提議呀?如果有,是關于看什么電影的,編號是多少呢?”
?
- 朋友們收到消息后,會查看自己收到過的提議編號。如果你的編號比他們之前收到的都大,他們就會回復你,比如有的朋友會說:“我之前沒收到過提議。”有的朋友可能會說:“我之前收到過提議看電影A,編號是0。”同時,他們會承諾不再接受編號小于1的提議。
?
提議階段
?
- 你收到朋友們的回復后,發現有朋友提到了之前看過的提議看電影A,編號是0,而你的編號是1更大,所以你可以選擇自己重新提議看電影B,也可以選擇就提議看電影A。然后你把你的提議(比如看電影B,編號是1)發給朋友們。
?
- 朋友們收到你的提議后,會檢查這個提議的編號是不是不小于他們之前見過的最大編號,并且他們之前沒有承諾過不接受這個提議。如果滿足條件,他們就會接受這個提議,比如同意一起去看電影B。
?
學習階段
?
- 當有超過一半的朋友都接受了看電影B這個提議,那么就相當于大家達成了一致,決定一起去看電影B。然后大家就可以一起去看電影,保證了所有人的行動一致。
?
在這個過程中,即使有朋友一開始沒收到消息,或者中間有消息延遲等情況,只要最終大家都按照這個流程來,就能保證最終能就看哪部電影達成一致,就像Paxos算法在分布式系統中保證數據一致性一樣。
Paxos算法這樣的一致性算法的設計思路是基于對分布式系統中一致性問題的深刻理解和長期的研究探索逐漸形成的,主要考慮以下幾個方面:
?
問題分析
- 分布式系統中存在節點故障、網絡延遲、消息丟失等問題,要保證數據在多個節點間的一致性,需要設計一種能在復雜環境下達成共識的機制。
- 借鑒現實生活中類似議會投票等協商場景的經驗,思考如何通過類似的投票、協商過程讓分布式系統中的節點就某個值達成一致。
?
關鍵原則確定
- 安全性原則是確保只有被多數節點認可的值才能被選定,防止出現不一致的情況。就像在選舉中,只有獲得多數選票的候選人才能當選,保證結果的唯一性和確定性。
- 活性原則是保證系統能夠不斷推進,不會因為某些故障或異常而陷入死循環或無法做出決策的狀態。例如,通過給提議編號等方式,讓系統能夠區分不同的提議,避免重復或無效的提議導致系統停滯。
?
逐步構建算法
- 先設計準備階段,讓提議者了解系統中已有的提議情況,同時讓接受者承諾不接受低編號提議,為后續提議的順利進行奠定基礎。這一步就像在會議前先收集各方意見,確定大家的基本立場。
- 再設計提議階段,提議者根據準備階段的反饋確定提議值并發送給接受者,接受者根據一定規則決定是否接受提議。這個過程類似會議中的討論和表決環節。
- 最后通過學習階段,讓系統中的其他節點能夠得知達成一致的結果,從而實現整個系統的一致性更新。
?
通過這樣從問題分析到關鍵原則確定,再到逐步構建算法的過程,經過不斷地理論推導、實踐驗證和優化,最終形成了Paxos算法這種能夠有效保證分布式系統一致性的經典算法。
?
?
rabbitmq 6種模式

?
sql連接
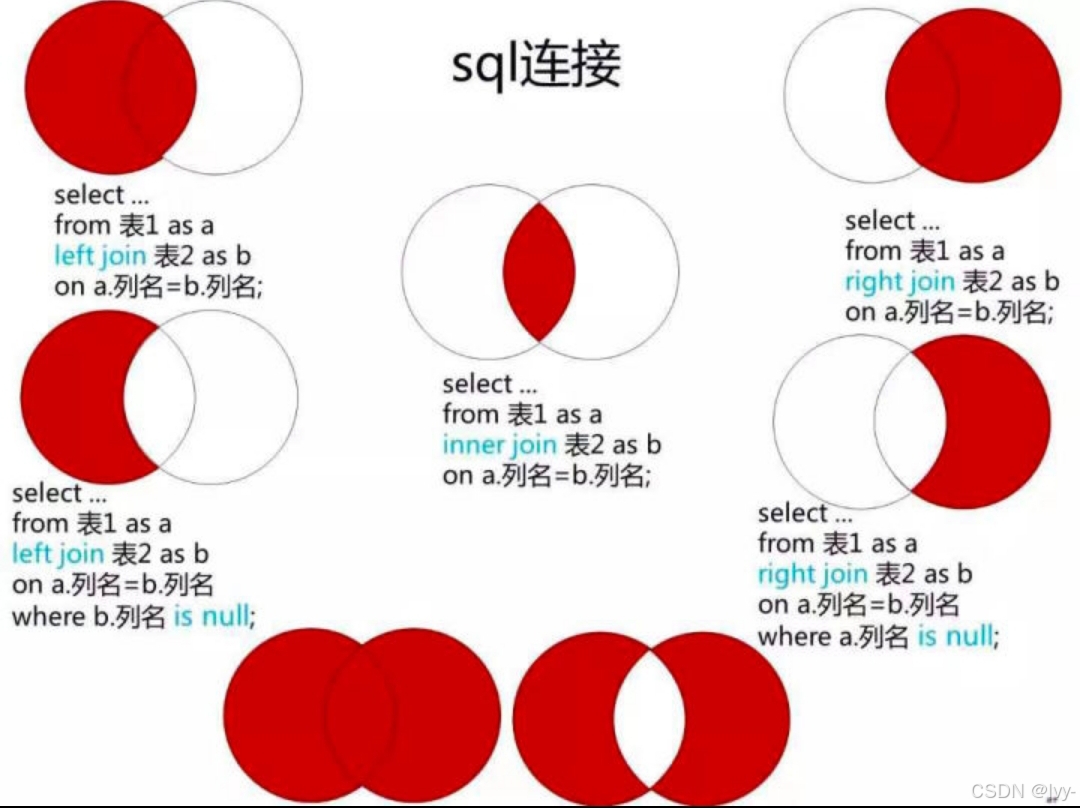
?select p.FirstName,p.LastName,a.City,a.State
from
person p left join address a
on
p.personid=a.personid
?
2的冪再和,二進制取模相加==n

?1.?分解n為2的冪次:
?
- 利用二進制特性,n的每一位1對應一個唯一的2的冪次(如n=10=8+2=23+21,對應powers=[2,8])。
?
- 通過不斷對n取余和整除2,提取每一位二進制位,將對應的冪次存入?powers?數組。
?
2.?處理查詢:
?
- 每個查詢給出一個區間?[l, r]?,表示求?powers[l] * powers[l+1] * ... * powers[r]?的結果。
?
- 由于結果可能很大,每次乘法后都對?1e9+7?取模(利用模運算性質防止溢出)。
?
3.?注意點:
?
- 使用?long long?存儲中間結果,避免整數溢出。
?
- ?powers?數組的下標直接對應查詢中的區間端點(如查詢?[0,2]?表示取前3個冪次相乘)。
?
示例理解:
- - 若?n=15?(二進制?1111?),則?powers = [1,2,4,8]?。
- - 查詢?[0,2]?對應計算?1*2*4=8?,查詢?[1,3]?對應?2*4*8=64?。
class Solution {
public:
? ? vector<int> productQueries(int n, vector<vector<int>>& queries) {
? ? ? ? // 造powers數組
? ? ? ? vector<int> powers;
? ? ? ? // 由n變到1powers數組
? ? ? ? for(int i=0,i1=1,j=0;n>0;)
? ? ? ? {
? ? ? ? ? ? i=n%2;
? ? ? ? ? ? if(i==1) {powers.push_back(i1);j++;}
? ? ? ? ? ? n/=2;i1*=2;
? ? ? ? }
? ? ? ? // return powers;
? ? ? ? // 造answers數組
? ? ? ? vector<int> answers;
? ? ? ? for(int i=0; i<queries.size(); i++)
? ? ? ? {
? ? ? ? ? ? long long ans=1;
? ? ? ? ? ? int c=1e7;
? ? ? ? ? ? for(int k=queries[i][0]; k<=queries[i][1]; k++)
? ? ? ? ? ? {ans=((ans%c)*(powers[k]%c))%c;}
? ? ? ? ? ? ?//求區間乘積
? ? ? ? ? ? //利用了(a*b)%c=((a%c)*(b%c))%c 拆分取模,防止溢出
? ? ? ? ? ? answers.push_back(ans);
? ? ? ? }
? ? ? ? return answers;
? ? }
};
?
爬樓梯
class Solution {
public:
? ? int climbStairs(int n)?
? ? {
? ? ? ? if(n<3) return n;
? ? ? ? vector<int> dp(n+1);
? ? ? ? dp[1]=1,dp[2]=2;
? ? ? ??
? ? ? ? for(int i=3;i<=n;i++)
? ? ? ? {
? ? ? ? ? ? dp[i]=dp[i-1]+dp[i-2];
? ? ? ? }
? ? ? ? return dp[n];
? ? }
};
接雨水

這段代碼用「棧」來計算接雨水的量,核心邏輯是:
從左到右遍歷每個柱子,用棧記錄「可能成為左邊邊界」的柱子下標。
當遇到更高的柱子(右邊界)時,計算兩者之間的「凹槽儲水量」:
?
1.?彈出棧頂(中間柱子),若棧空則無法形成凹槽,跳過。
2.?確定左右邊界:新棧頂是左邊界,當前下標是右邊界。
3.?計算高度差:左右邊界的最小值 - 中間柱子高度,得到儲水高度。
4.?計算寬度:右邊界下標 - 左邊界下標 - 1,乘高度得到水量,累加到結果。
?
舉例:柱子高度為 ?[0,1,0,2,1,0,1,3,2,1,2,1]?,
遍歷到 ?i=3?(高度2)時,棧中是 ?[0,1]?(高度0,1),
彈出1(高度1),左邊界是0(高度0),右邊界是3(高度2),
儲水高度 = min(0,2) - 1 = -1?不,這里實際是 min(左邊界高度, 右邊界高度) - 中間高度,
左邊界高度是 ?height[0]=0?,右邊界是 ?height[3]=2?,中間是 ?height[1]=1?,
所以儲水高度是 0-1?不對! 哦這里發現描述有誤,正確邏輯是:只有左右邊界都高于中間柱子時才有儲水,
所以當右邊界高度 > 中間柱子時,左邊界必須存在且高度 > 中間柱子,
此時儲水高度 = min(左邊界高度, 右邊界高度) - 中間高度,
寬度是右邊界下標 - 左邊界下標 - 1。
?
代碼通過棧動態維護左右邊界,逐個計算每個凹槽的水量,最終總和就是答案。
?
int trap(vector<int>& height)
{
? ? int ans = 0;
? ? stack<int> st;
? ? for (int i = 0; i < height.size(); i++)
? ? {
? ? ? ? while (!st.empty() && height[st.top()] < height[i])
? ? ? ? {
? ? ? ? ? ? int cur = st.top();
? ? ? ? ? ? st.pop();
? ? ? ? ? ? if (st.empty()) break;
? ? ? ? ? ? int l = st.top();
? ? ? ? ? ? int r = i;
? ? ? ? ? ? int h = min(height[r], height[l]) - height[cur];
? ? ? ? ? ? ans += (r - l - 1) * h;
? ? ? ? }
? ? ? ? st.push(i);
? ? }
? ? return ans;
}
雙指針

?
?class Solution {
public:
? ? int trap(vector<int>& height) {
? ? ? ? int ans = 0, left = 0, right = height.size() - 1, pre_max = 0, suf_max = 0;
? ? ? ? while (left < right) {
? ? ? ? ? ? pre_max = max(pre_max, height[left]);
? ? ? ? ? ? suf_max = max(suf_max, height[right]);
? ? ? ? ? ? ans += pre_max < suf_max ? pre_max - height[left++] : suf_max - height[right--];
? ? ? ? }
? ? ? ? return ans;
? ? }
};
?
dfs超時優化

注意到 十的九次方?
原代碼,超時
class Solution {
public:
? ? int n=0;
? ? vector<int> ans;
? ? int findKthNumber(int n, int k)?
? ? {
? ? ? ? this->n=n;
? ? ? ? for(int i=1;i<10;i++)
? ? ? ? {
? ? ? ? ? ? dfs(i);
? ? ? ? }
? ? ? ?
? ? ? ? return ans[k-1];
? ? }
? ??
? ? void dfs(int num)
? ? ? ? {
? ? ? ? ? ? if(num>n)
? ? ? ? ? ? {
? ? ? ? ? ? ? ? return;
? ? ? ? ? ? }
? ? ? ? ? ??
? ? ? ? ? ? ans.push_back(num);
? ? ? ? ? ? for(int i=0;i<10;i++)
? ? ? ? ? ? {
? ? ? ? ? ? ? ? dfs(num*10+i);
? ? ? ? ? ? }
? ? ? ? }
};
數學優化
class Solution {
public:
? ? long getCount(long prefix, long n) {
? ? ? ? long cur = prefix;
? ? ? ? long next = cur + 1;
? ? ? ? long count = 0;
? ? ? ? while(cur <= n) {
? ? ? ? ? ? count += min(n+1, next) - cur;
? ? ? ? ? ? cur *= 10;
? ? ? ? ? ? next *= 10;
? ? ? ? }
? ? ? ? return count;
? ? }
? ? int findKthNumber(int n, int k) {
? ? ? ? long p = 1;
? ? ? ? long prefix = 1;
? ? ? ? while(p < k) {
? ? ? ? ? ? long count = getCount(prefix, n);
? ? ? ? ? ? if (p + count > k) {
? ? ? ? ? ? ? ? /// 說明第k個數,在這個前綴范圍里面
? ? ? ? ? ? ? ? prefix *= 10;
? ? ? ? ? ? ? ? p++;
? ? ? ? ? ? } else if (p+count <= k) {
? ? ? ? ? ? ? ? /// 說明第k個數,不在這個前綴范圍里面,前綴需要擴大+1
? ? ? ? ? ? ? ? prefix++;
? ? ? ? ? ? ? ? p += count;
? ? ? ? ? ? }
? ? ? ? }
? ? ? ? return static_cast<int>(prefix);
? ? }
};
?
優化思路:
?
1.?字典序規則:
像查字典一樣,先比首位,再比第二位。例如:
?
- - 1開頭的數(1,10,11,12…)比2開頭的數(2,20,21…)更小。
?
2.?關鍵函數?getCount?:
計算以?prefix?(如1、10)開頭的數字有多少個≤n。
?
- - 比如?prefix=1?,n=20時,包含1、10-19、20(共1+10+1=12個)。
- - 計算方式:逐層擴展(1→10→100),每次算當前層有多少個數在n以內。
3.理解
- ?p++?是深入子節點找下一個數,
?
- ?p += count?是跳過當前前綴,去下一個前綴找。
十叉樹
把數字看作樹,用子樹大小判斷第k個數在左子樹還是右兄弟:
?
- - 子樹夠大:鉆進左子樹(?node*=10?)。
- - 子樹不夠大:跳過左子樹,去右兄弟(?node++?)。
通過這種方式,每次跳躍式減少k的范圍,效率極高(對數級時間復雜度)。
class Solution {
public:
? ? int findKthNumber(int n, int k) {
? ? ? ? // 逐層統計 node 子樹大小
? ? ? ? auto count_subtree_size = [&](int node) -> int {
? ? ? ? ? ? // 子樹大小不會超過 n,所以 size 用 int 類型
? ? ? ? ? ? // 但計算過程中的 left 和 right 會超過 int,所以用 long long 類型
? ? ? ? ? ? int size = 0;
? ? ? ? ? ? long long left = node, right = node + 1;
? ? ? ? ? ? while (left <= n) {
? ? ? ? ? ? ? ? // 這一層的最小值是 left,最大值是 min(right, n + 1) - 1
? ? ? ? ? ? ? ? size += min(right, n + 1LL) - left;
? ? ? ? ? ? ? ? left *= 10; // 繼續,計算下一層
? ? ? ? ? ? ? ? right *= 10;
? ? ? ? ? ? }
? ? ? ? ? ? return size;
? ? ? ? };
? ? ? ? int node = 1;
? ? ? ? k--; // 訪問節點 node
? ? ? ? while (k > 0) {
? ? ? ? ? ? int size = count_subtree_size(node);
? ? ? ? ? ? if (size <= k) { // 向右,跳過 node 子樹
? ? ? ? ? ? ? ? node++; // 訪問 node 右側兄弟節點
? ? ? ? ? ? ? ? k -= size; // 訪問子樹中的每個節點,以及新的 node 節點
? ? ? ? ? ? } else { // 向下,深入 node 子樹
? ? ? ? ? ? ? ? node *= 10; // 訪問 node 的第一個兒子
? ? ? ? ? ? ? ? k--; // 訪問新的 node 節點
? ? ? ? ? ? }
? ? ? ? }
? ? ? ? return node;
? ? }
};
?
線程

?
?模擬?貪心

要么都變成 1,要么都變成 -1,因此先枚舉要變成哪個。
剩下的問題就是一個經典的貪心。
由于乘以 -1 兩次之后會變回原數,因此每個下標最多選擇一次,且下標選擇的順序沒有關系。
不妨假設操作是從左到右進行的。
從左到右考慮每個下標,如果當前值不是目標值,由于后續操作只會影響右邊的數,再不操作就沒機會了,所以此時必須要選擇該下標。
按該貪心思路算出最少操作次數即可,復雜度 O(n) 。
思維題:想到傳遞的目標判斷即可
其實也還可以找奇偶的規律,但是還是這種更好
class Solution {
public:
? ? bool canMakeEqual(vector<int>& nums, int K) {
? ? ? ? int n = nums.size();
? ? ? ? // 所有值都變成 x 的最少操作次數
? ? ? ? auto check = [&](int x) {
? ? ? ? ? ? int cnt = 0;
? ? ? ? ? ? vector<int> vec = nums;
? ? ? ? ? ? // 從左到右考慮每個下標,如果不是目標值,必須操作
? ? ? ? ? ? for (int i = 0; i + 1 < n; i++) if (vec[i] != x) {
? ? ? ? ? ? ? ? vec[i] *= -1;
? ? ? ? ? ? ? ? vec[i + 1] *= -1;
? ? ? ? ? ? ? ? cnt++;
? ? ? ? ? ? }
? ? ? ? ? ? return vec[n - 1] == x && cnt <= K;
? ? ? ? };
? ? ? ? // 枚舉最后變成 1 還是 -1
? ? ? ? return check(1) || check(-1);
? ? }
};
總結:
1.?枚舉目標:結果只有兩種可能——全 ?1??或者全 ?-1??。所以我們分別試試這兩種情況,看哪種能實現(這就是 “枚舉” ,把可能的目標全列出來試)。
?
2.?貪心操作:確定目標(比如要全 ?1??)后,怎么操作最省次數?
?
- 規則是 “選一個下標 ?i??,?nums[i]??和 ?nums[i+1]??都變號” 。而且變號兩次等于沒變(比如 ?1??變 ?-1??再變 ?1??),所以每個位置最多操作一次,從左到右處理最合理 。
?
- 舉個例子:數字是 ?[-1, -1, 1]??,目標要全 ?1??。從左開始看,第一個數是 ?-1??(不是目標 ?1??),必須操作下標 ?0??,讓 ?nums[0]??和 ?nums[1]??變號,變成 ?[1, 1, 1]??,這樣一次就解決。如果不操作當前下標,后面操作不影響前面,就永遠變不成目標了,所以 “遇到不一樣的,必須當下操作” ,這就是貪心的 “貪”—— 抓住當下機會,保證結果最優。
?
移動模擬_優化
原代碼
class Solution {
public:
? ? int N;
? ? void move(char c, vector<int>& pos, vector<int>& t) {
? ? ? ? if (c == 'L') pos[1] -= 1;
? ? ? ? if (c == 'R') pos[1] += 1;
? ? ? ? if (c == 'U') pos[0] -= 1;
? ? ? ? if (c == 'D') pos[0] += 1; ? ? ? ?
? ? ? ? t = pos;
? ? }
? ? bool check(vector<int>& pos) {
? ? ? ? if (pos[0] >= 0 && pos[0] < N && pos[1] >= 0 && pos[1] < N) return true;
? ? ? ? else return false;
? ? }
? ? vector<int> executeInstructions(int n, vector<int>& startPos, string s) {
? ? ? ? vector<int> res(s.size());
? ? ? ? N = n;
? ? ? ? for (int i = 0; i < s.size(); i ++ ) {
? ? ? ? ? ? vector<int> tempos(startPos);
? ? ? ? ? ? int temres = 0;
? ? ? ? ? ? for (int j = i; j < s.size(); j ++ ) {
? ? ? ? ? ? ? ? vector<int> t(2);
? ? ? ? ? ? ? ? move(s[j], tempos, t); ? ? ? ? ? ? ??
? ? ? ? ? ? ? ? if (check(t)) temres ++ ,tempos = t;
? ? ? ? ? ? ? ? else break;
? ? ? ? ? ? }
? ? ? ? ? ? res[i] = temres;
? ? ? ? }
? ? ? ? return res;
? ? }
};
優化:
改用迭代器并內聯函數的 C++ 代碼(主要修改循環和容器操作部分):
class Solution {
public:
? ? int N;
? ? // 內聯移動函數(用引用避免拷貝)
? ? inline void move(char c, vector<int>& pos, vector<int>& t) {
? ? ? ? switch(c) {
? ? ? ? ? ? case 'L': pos[1]--; break;
? ? ? ? ? ? case 'R': pos[1]++; break;
? ? ? ? ? ? case 'U': pos[0]--; break;
? ? ? ? ? ? case 'D': pos[0]++;?
? ? ? ? }
? ? ? ? t = pos; // 更新目標位置
? ? }
? ? // 內聯邊界檢查
? ? inline bool check(const vector<int>& pos) {
? ? ? ? return pos[0] >= 0 && pos[0] < N && pos[1] >= 0 && pos[1] < N;
? ? }
?
? ? vector<int> executeInstructions(int n, vector<int>& startPos, string s) {
? ? ? ? vector<int> res(s.size());
? ? ? ? N = n;
? ? ? ??
? ? ? ? // 使用迭代器遍歷字符串
? ? ? ? for(auto it_i = s.begin(); it_i != s.end(); ++it_i) {
? ? ? ? ? ? vector<int> currentPos = startPos;
? ? ? ? ? ? int count = 0;
? ? ? ? ? ??
? ? ? ? ? ? // 從當前迭代器位置開始遍歷
? ? ? ? ? ? for(auto it_j = it_i; it_j != s.end(); ++it_j) {
? ? ? ? ? ? ? ? vector<int> tempPos(2);
? ? ? ? ? ? ? ? move(*it_j, currentPos, tempPos); // 傳入字符值
? ? ? ? ? ? ? ??
? ? ? ? ? ? ? ? if(check(tempPos)) {
? ? ? ? ? ? ? ? ? ? count++;
? ? ? ? ? ? ? ? ? ? currentPos = tempPos; // 更新當前位置
? ? ? ? ? ? ? ? } else {
? ? ? ? ? ? ? ? ? ? break; // 越界則終止
? ? ? ? ? ? ? ? }
? ? ? ? ? ? }
? ? ? ? ? ? res[it_i - s.begin()] = count; // 計算索引
? ? ? ? }
? ? ? ? return res;
? ? }
};
?
主要改動點:?
1.?函數內聯:使用 ?inline? 關鍵字聲明 ?move? 和 ?check? 函數(現代編譯器可能自動優化,但顯式聲明更清晰)
?
2.?迭代器替代索引:
- 外層循環用 ?s.begin()?/?end()? 迭代器遍歷
- 內層循環從當前迭代器位置 ?it_i? 開始
- 通過 ?it_i - s.begin()? 計算結果數組索引
?
3.?代碼優化:
- ?switch? 替代多個 ?if? 提高分支效率
- ?currentPos? 直接修改減少拷貝(原代碼中 ?tempos = t? 可直接操作 ?currentPos?)
- ?const? 修飾 ?check? 函數參數避免意外修改
?
注意:C++ 中容器迭代器在動態擴容時可能失效,但此處 ?string? 是固定長度,迭代器始終有效,無需擔心此問題。
內聯函數
內聯函數是一種用 ?inline? 關鍵字聲明的特殊函數,目的是讓編譯器在編譯時直接把函數代碼「嵌入」到調用它的地方,避免普通函數調用的「跳轉開銷」,提高程序運行速度。
?
舉個簡單例子:
假設有個函數計算兩數之和:
int add(int a, int b) {?
? ? return a + b;?
}
?
普通調用時,程序會「跳轉到函數地址執行代碼,再跳轉回來」。
如果聲明為內聯函數:
inline int add(int a, int b) {?
? ? return a + b;?
}
編譯時,編譯器會把 ?add(3,5)? 直接替換成 ?3+5?,就像你直接寫在代碼里一樣,省去了跳轉步驟。
?
關鍵特點:
1.?編譯時替換:不是運行時調用,而是編譯階段直接「展開代碼」。
2.?適合簡單函數:通常用于代碼量少(如幾行)、調用頻繁的函數(比如循環里的小操作)。
3.?可能被編譯器忽略:最終是否內聯由編譯器決定(太復雜的函數會被拒絕)。
?
優點 vs 缺點:
- - 優點:減少函數調用開銷,提升執行效率。
- - 缺點:如果函數被多次調用,會導致目標代碼體積增大(用空間換時間)。
總結:內聯函數就像「把常用的小工具直接粘在使用的地方」,省去了拿工具的步驟,但粘太多會占地方。
?
進行加密和解密的基本操作)

)













)


