


算法系列八:非比較排序
一、計數排序
1.實現
1.1步驟
1.2代碼
2.性質
2.1穩定性
2.1.1從前往后前始版:
2.1.2從后往前末始版:
2.2復雜度
2.2.1時間復雜度
2.2.2空間復雜度
二、桶排序
1.實現
1.1步驟
1.2代碼
2.穩定性
三、基數排序
1.原理
2.代碼
鴿巢原理
鴿子歸巢,待排序數據歸到有序組群中按大小歸進有序組群來排,數越大,歸到的有序組就在越后的,數越小,歸到的有序組就在越前的
- 如果有序組以一個元素一個元素劃分的,實現的是元素組歸巢排序,即計數排序
- 如果有序組按范圍多個元素為一組劃分的,實現的是范圍組歸巢排序,即桶排序
一、計數排序
1.實現
1.1步驟
- 開辟數據范圍內的所有元素都有各自對應的元素組巢穴,范圍內一共有多少種個數據,就開辟每種個數據都有對應的多大的數組,比如90(max) - 10(min) = 80(種個數據)
- 歸巢時,通過該數據-數據范圍內的最小值得到所歸巢的下標,然后在數組元素巢中計數表示歸巢
- 因為巢內只有一種個數據直接就是有序的,所以所有數據歸完巢在巢層面有序時所有數據就已經有序了,最后將它們按順序地趕出巢加回去即得原來有序的數據
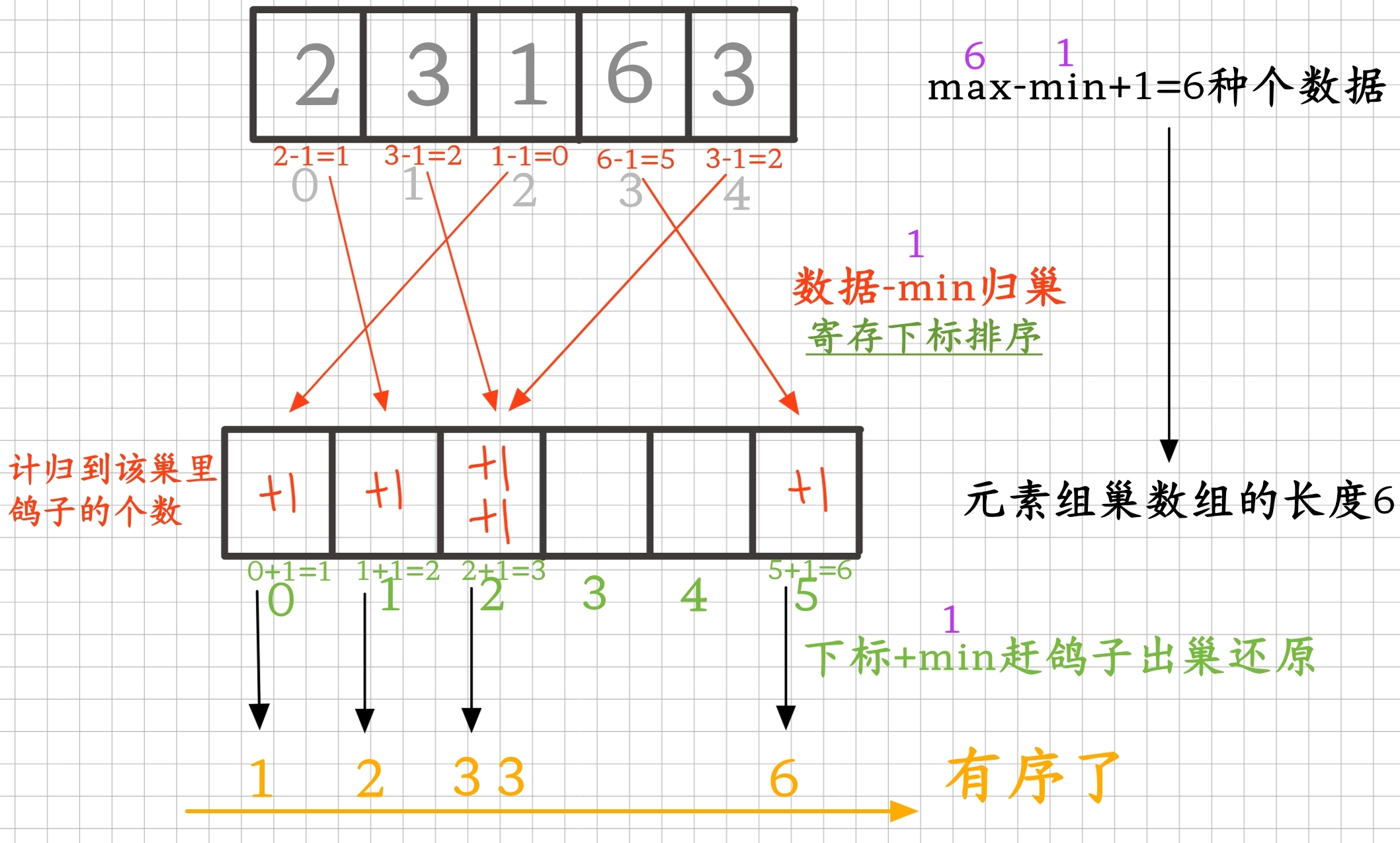
1.2代碼
public static void countSort(int[] array) {//1.求當前數據的最大值和最小值int minVal = array[0];int maxVal = array[0];for (int i = 1; i < array.length; i++) {if(array[i] < minVal) {minVal = array[i];}if(array[i] > maxVal) {maxVal = array[i];}}//2.根據數據最大值和最小值來確定元素組巢穴數組的大小int[] count = new int[maxVal-minVal+1];//3.遍歷原來的數據進行歸巢排序for (int i = 0; i < array.length; i++) {count[array[i]-minVal]++;}//4.將元素組巢穴里已排好序的數據按順序寫回arrayint index = 0;//重新表示array數組的下標for (int i = 0; i < count.length; i++) {while (count[i] > 0) {array[index] = i+minVal;index++;count[i]--;}}}
}
2.性質
2.1穩定性
將每個數據都歸到巢中完成有序時,根據巢中有序來的元素的計數個數,可以將巢改裝成裝每種個元素有序排的始位置,通過對應順序遍歷原數組將數據正確穩定地放在排好序的各自位置上,能實現穩定的排序,所以計數排序是穩定的排序
2.1.1從前往后前始版:
原本巢中裝的是鴿子的計數數量,現在巢里面改裝成裝種個鴿子從前往后的起始位置來進行排序:
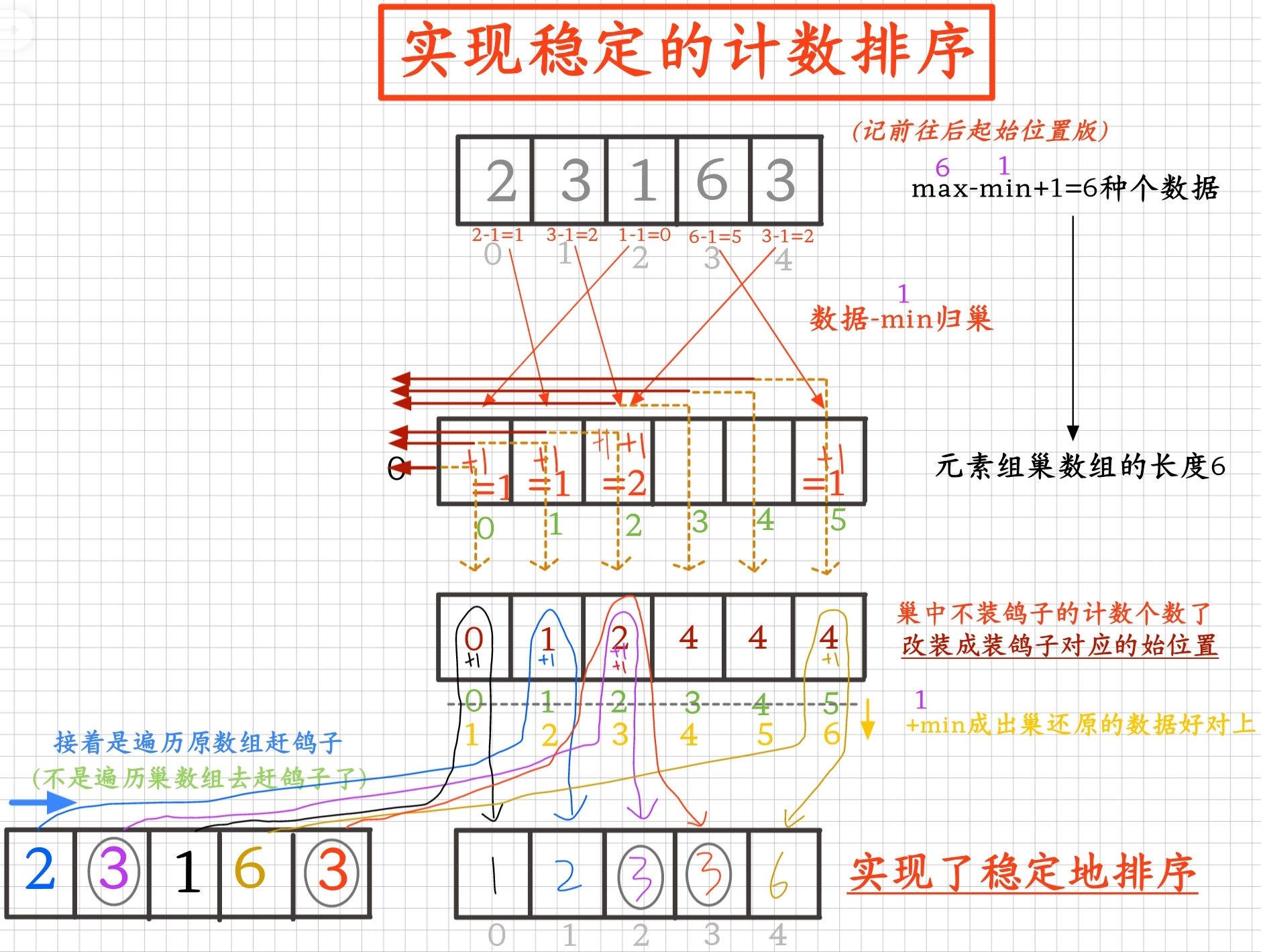
2.1.2從后往前末始版:
?巢里面改裝成裝種個鴿子從后往前的起始位置來進行排序:
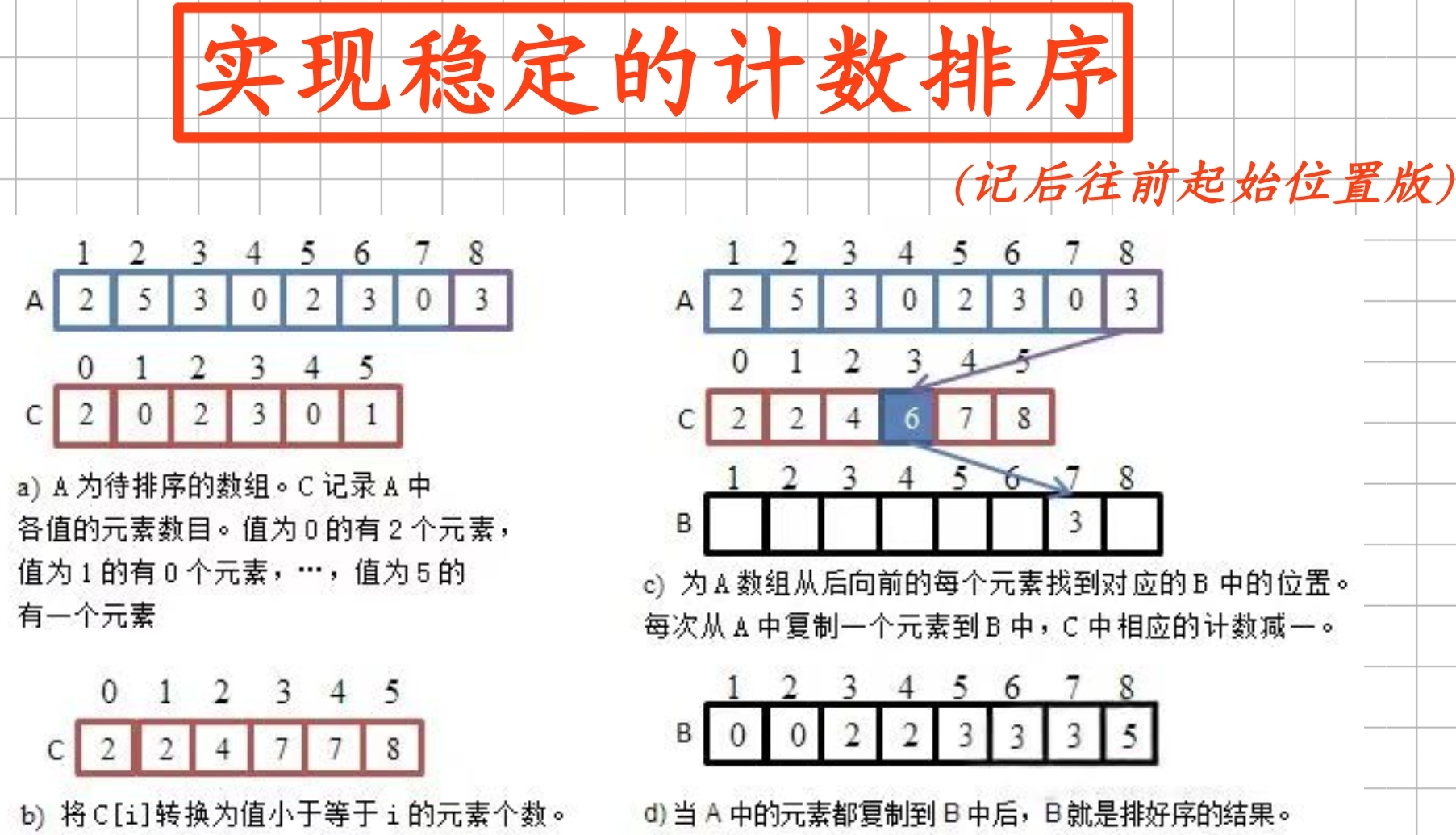
2.2復雜度
2.2.1時間復雜度
找最大最小值確定范圍種個數據遍歷原數組用了n,原數組數據每個去歸巢用了n,范圍x種個元素巢每個去趕,所以時間復雜度為2n + x,即O(n+x)
2.2.2空間復雜度
范圍x種個數據需要開辟x個元素巢的數組,所以空間復雜度為O(x)
二、桶排序
1.實現
1.1步驟
- 開辟數據范圍內所有元素都有對應的范圍數組組巢穴,將所有數據入范圍組巢穴先進行第一輪巢穴外的排好序,此時巢外已經有序了
- 再進行第二輪各自巢穴內的排好序,此時就巢外、巢內都有序所有數據都有序了
- 最后按順序地將它們從數組巢中趕出即得有序的數據

1.2代碼
public static int[] bucketSort(int[] arr) {// 邊界條件:空數組或單個元素直接返回if (arr.length <= 1) {return arr.clone();}// Step 1: 確定數據范圍int minVal = Integer.MAX_VALUE;int maxVal = Integer.MIN_VALUE;for (int num : arr) {if (num < minVal) minVal = num;if (num > maxVal) maxVal = num;}// 處理所有元素相同的情況if (maxVal == minVal) {return arr.clone();}// Step 2: 初始化桶int bucketCount = (int) Math.sqrt(arr.length) + 1; // 桶數量=數組長度的平方根(經驗值)double bucketRange = (double)(maxVal - minVal) / bucketCount;List<List<Integer>> buckets = new ArrayList<>(bucketCount);for (int i = 0; i < bucketCount; i++) {buckets.add(new ArrayList<>());}// Step 3: 元素分配到桶中for (int num : arr) {// 計算元素應該屬于哪個桶int index = (int)((num - minVal) / bucketRange);// 處理最大值剛好落在最后一個桶外的情況if (index == bucketCount) index--;buckets.get(index).add(num);}// Step 4: 對每個桶內部排序for (List<Integer> bucket : buckets) {Collections.sort(bucket); // 使用內置排序算法,決定了桶排序的穩定性}// Step 5: 合并桶int[] sortedArr = new int[arr.length];int idx = 0;for (List<Integer> bucket : buckets) {for (int num : bucket) {sortedArr[idx++] = num;}}return sortedArr;}2.穩定性
穩定性取決于在第二輪巢內開始排相同大小的元素時所用的排序方法是否具有穩定性
三、基數排序
1.原理
- 先進行個位排序,能實現個位一位數有序
- 個位有序下,再進行十位優先排序,能實現十位個位兩位數有序
- 十個位有序下,再進行百位優先排序,能實現百位十位個位三位數有序
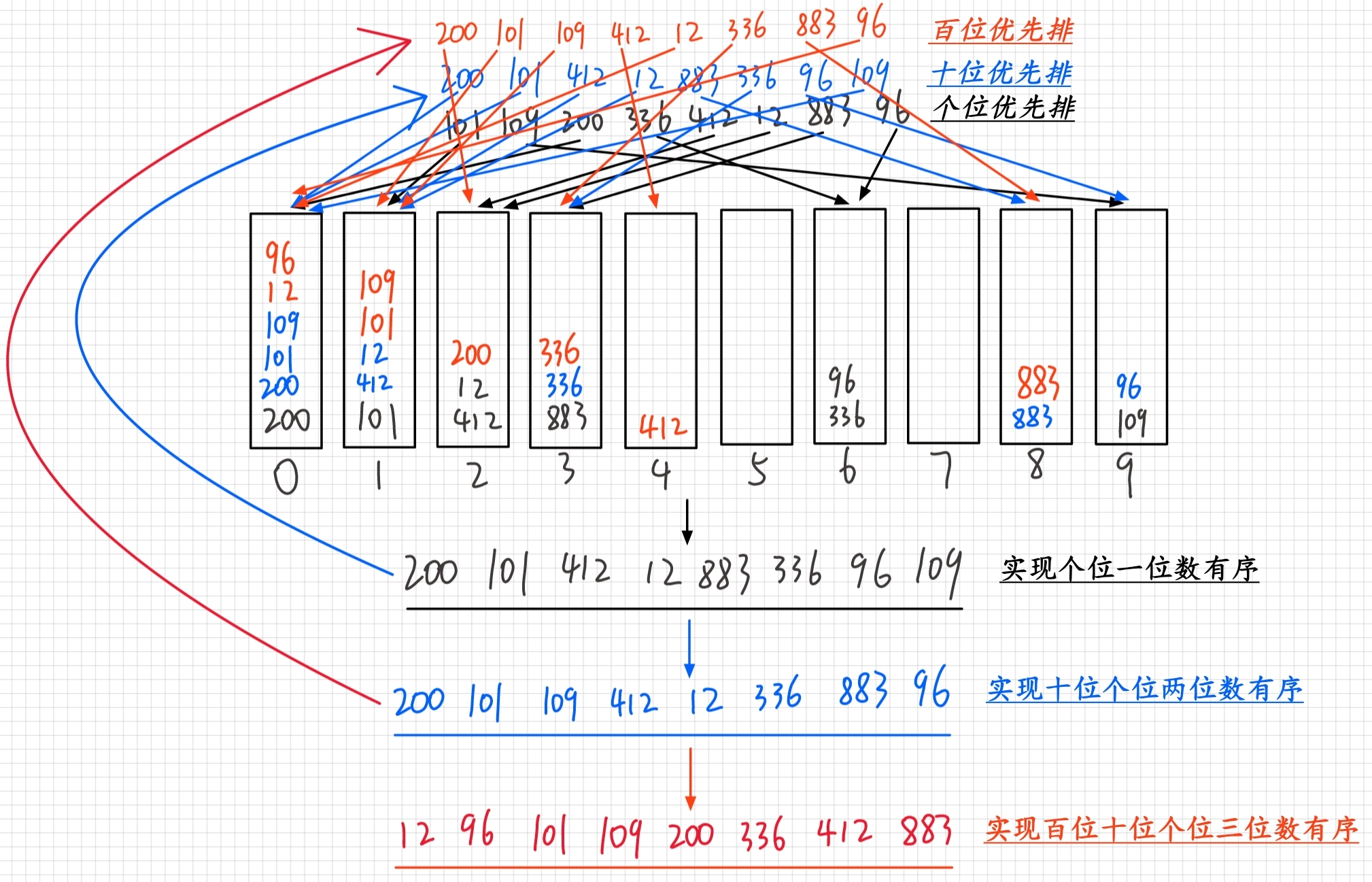
2.代碼
public static int[] radixSort(int[] arr) {if (arr.length <= 1) {return arr.clone();}// Step 1: 確定最大數的位數int maxNum = Integer.MIN_VALUE;for (int num : arr) {if (num > maxNum) maxNum = num;}// Step 2: 按每位進行計數排序(從低位到高位)int exp = 1; // 從個位開始while (maxNum / exp > 0) {// 初始化10個數字桶(0-9)List<List<Integer>> buckets = new ArrayList<>(10);for (int i = 0; i < 10; i++) {buckets.add(new ArrayList<>());}// 按當前位分配到桶中for (int num : arr) {int digit = (num / exp) % 10; // 提取當前位的數字buckets.get(digit).add(num);}// 重組數組int idx = 0;for (List<Integer> bucket : buckets) {for (int num : bucket) {arr[idx++] = num;}}exp *= 10; // 處理更高位}return arr;}

)







)







技術的實例)
編寫單元測試)