全文鏈接：https://tecdat.cn/?p=36979

原文出處：拓端數據部落公眾號

廣義加法模型（Generalized Additive Models, GAMs）作為一種高度靈活的統計工具，顯著擴展了廣義線性模型（Generalized Linear Models, GLMs）的框架。GAMs的核心思想在于，將GLM中的一個或多個線性預測變量替換為這些變量的平滑函數，從而允許模型捕捉預測變量與條件響應之間復雜且非線性的關系，而無需事先對這些關系的具體形態做出假設。這一過程通過引入懲罰平滑樣條技術實現，該方法在保持模型靈活性的同時，有效防止了過擬合現象。

GAMs的工作原理根植于基展開（basis expansion）的概念之中。簡而言之，基展開意味著將協變量（在此語境下，如時間等）映射到一組精心設計的基函數上，這些基函數旨在全面覆蓋協變量觀測值的范圍。一種常用的基函數類型是三次回歸基（cubic regression splines），它們能夠靈活地適應數據的局部特征。

值得注意的是，除了三次回歸基外，還有多種類型的基展開方法可用于構建懲罰平滑模型，包括但不限于多維平滑技術，用于處理具有多個協變量的復雜情況；空間平滑技術，特別適用于具有空間相關性的數據；以及單調平滑技術，確保模型輸出隨協變量單調變化，以滿足特定領域的分析需求。這些多樣化的基展開方法為GAMs提供了廣泛的應用前景和強大的建模能力。

何時應使用廣義加法模型？

GAM之所以備受推崇，主要歸因于其在處理復雜數據關系上的獨特優勢。具體而言，當研究者面臨以下情境時，GAM成為強有力的分析工具：

1. 非線性關系探索：當響應變量與預測變量間可能存在未知的非線性關系時，GAM能靈活捕捉這些復雜模式。
2. 形式無關性：無需預設關系形式，GAM通過數據驅動的方式自動學習最佳擬合模型。
3. 高效捕獲非線性效應：相比傳統高階多項式，GAM能以更優雅的方式捕獲非線性效應，同時規避其潛在的過擬合和解釋復雜性。
4. 穩健性：在追求模型擬合精度的同時，GAM通過懲罰平滑技術有效控制過擬合風險。

環境設置和初始 GAM 模型

現在，加載數據。這些數據包含草種耐寒性實驗的測量值

檢查數據結構和維度

dplyr::glimpse(CO2)

現在對建模進行一些操作

plant <- CO2 |>as_tibble() |>rename(plant = Plant, type = Type, treatment = Treatment) |>mutate(plant = factor(plant, ordered = FALSE))

我為這些數據擬合了一個廣義加性模型，指定了每個截距之間的參數交互作用以及隨機（分層）截距，并使用二氧化碳吸收 作為非負的實值響應。非線性部分允許二氧化碳濃度的非線性效應隨不同水平的冷處理變量而變化。

看看這個模型的總結

這里似乎有很多“重大”影響，但我們到底如何解釋這些呢？

?

標記的系數是控制這些樣條形狀的基函數權重。但是，如果不能完全理解這些基本函數是什么樣子的，以及它們如何共同作用形成樣條曲線。

現在，我將介紹 3 個步驟，您可以使用這些步驟來幫助解釋和報告來自 GAMS 的非線性效應。

第 1 步：可視化 GAM 輸出

到目前為止，視覺效果是我們理解 GAM 的最佳首選工具。

在鏈路（或鏈接）尺度上繪制GAM（廣義加性模型）的效應時，用戶最常采用的可視化手段是部分效應圖（Partial Effects Plots）。這些圖形在鏈路尺度上直觀地展示了各個平滑函數（Smooth Functions）的單獨分量效應，此過程中假設模型中的其他所有項均被固定為零（即，保持其他因素不變，僅關注某一特定預測變量的影響）。由于多數平滑項在作圖時會被中心化為零以提高可解釋性，因此這些圖形易于解讀，使得用戶能夠迅速獲得關于變量間關系的初步理解。

具體而言，若要在GAM中查看特定平滑項（如處理因素“nonchilled treatment”）的部分效應，用戶可以通過選擇該平滑項并觀察其在鏈路尺度上的表現來實現。

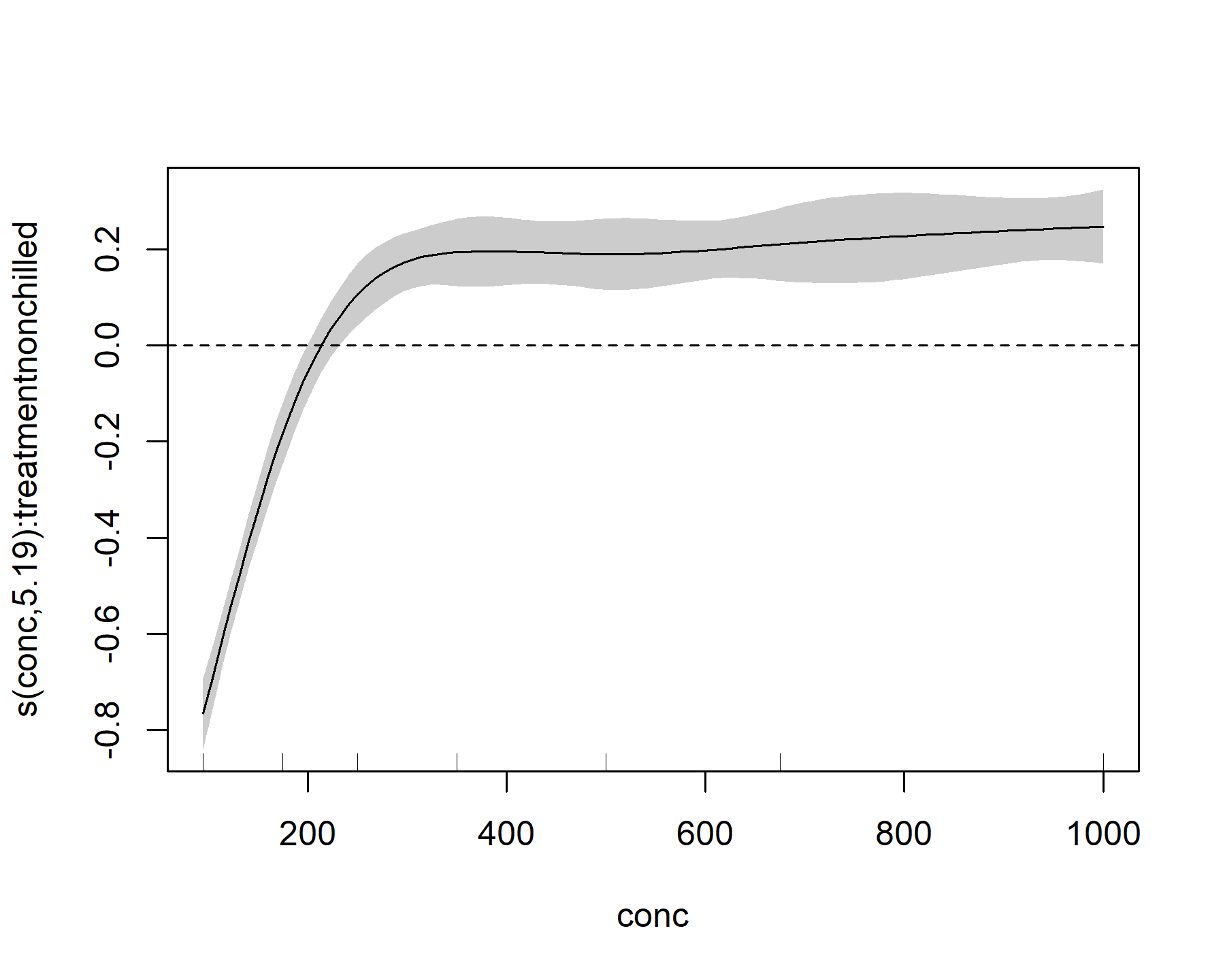
該圖顯示，對于 的較小值，對線性預測變量的影響大多為負值（低于零），但對于 的中間值，它很快就會變為正值（高于零）。然后，它開始在較大的值處趨于穩定。我們還可以看看其他層次的影響

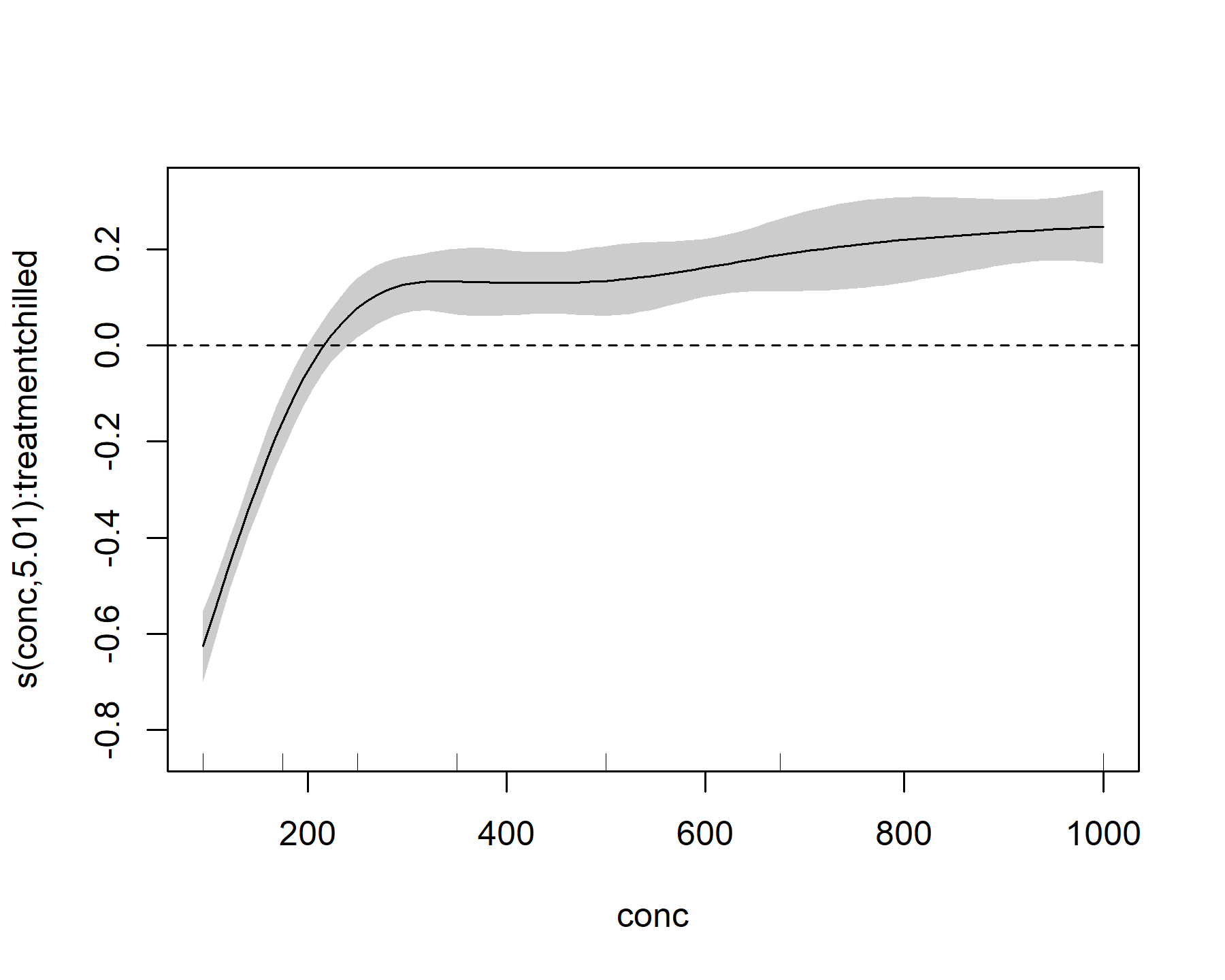
這個圖看起來大致相似，但效果并不完全相同。

在探討廣義加性模型（GAMs）的效應時，確實需要注意其可視化表示的局限性和如何更全面地理解模型結果。

GAM效應的可視化局限性

盡管在鏈路尺度上繪制GAM的部分效應圖是用戶常用的可視化手段，但這種方法有其內在的局限性。這些圖主要展示了在保持其他所有預測變量為零（或基準水平）的情況下，單個平滑函數對響應變量的預期影響。然而，這種“孤立”的展示方式可能無法全面反映預測變量之間的交互作用以及它們對響應變量的綜合影響。

復雜模型結構的挑戰

當GAM模型包含多個平滑項和交互項時（如y ~ s(rain) + s(temp) + s(year) + ti(rain, temp) + ti(rain, year) + ti(temp, year)），單一預測變量的效應往往分散在多個平滑函數中，這使得直接解釋每個平滑項變得困難。此外，如果模型采用對數鏈接函數等非線性鏈接，部分效應圖在鏈路尺度上的展示可能與實際尺度上的影響存在顯著差異。

超越鏈路尺度的分析

為了更全面地理解GAM的效應，我們需要超越簡單的鏈路尺度部分效應圖。以下是一些建議的方法：

1. 計算并繪制平均平滑效果：利用適當的統計軟件包（如R中的mgcv和ggeffects或margins包），可以計算并繪制考慮所有其他預測變量影響的平均平滑效果圖。這樣的圖能夠更好地反映預測變量在實際情境下的綜合影響。

2. 轉換到實際尺度：如果模型使用了非線性鏈接函數，應嘗試將鏈路尺度上的效應轉換為實際尺度（如原始數據尺度或概率尺度），以便更直觀地解釋模型結果。

3. 比較不同條件下的效應：通過計算和比較不同治療組或不同協變量水平下的效應，可以更深入地了解預測變量如何影響響應變量，以及這些影響在不同條件下如何變化。

4. 使用更高級的繪圖和摘要工具：采用專門的統計繪圖和摘要工具（如ggeffects、sjPlot等R包），可以方便地生成各種類型的效應圖，包括條件效應圖、交互效應圖等，從而更全面地展示GAM的復雜結構。

當然，我們可以很容易地將這些圖拆分為：

在探索廣義加性模型（GAMs）時，了解平滑函數斜率的變化對于深入理解模型行為及其在不同協變量水平下的影響至關重要。

首先，需要注意的是，plot_predictions()函數通常不直接支持繪制斜率。但是，您可以使用與這些包相關或獨立的函數來計算平滑函數的一階導數，并使用圖形化工具（如ggplot2）來展示這些斜率。

該圖更清楚地表明，在我們達到 260 附近的值之前，斜率是正的，超過該值，函數將趨于平穩。

如何在結果量表上繪制平滑效應？

在響應量表上繪制 GAM 效應

我們現在可以選擇在這些圖上顯示觀測值

plot_predictions(model_1, co

這是再次的平均平滑度，但這次是在響應變量的尺度上。

這些繪圖增強了我們對擬合模型進行質疑和評估的能力。在解讀或報告GAM中的函數時，您可以考慮以下幾個基本問題來啟動分析：

• 該函數是否在其定義域內達到漸近線？
• 函數圖像是劇烈波動還是展現出平滑的趨勢？
• 函數是否存在多個峰值或模式？這些模式在實際應用中是否有合理解釋？
• 是否存在數據點稀疏的區域，且該區域函數的不確定性相應增加？
• 是否有明顯的異常點，導致函數反應異常強烈？

此外，如果您有興趣進一步探索，確實可以在響應尺度上直接繪制斜率圖，以觀察函數變化率隨協變量的變化。

到目前為止，您可能對這些預測的來源感到好奇，這正是引入我們解釋GAM的下一個有力工具——模擬的恰當時機。

第2步：從擬合的GAM模型進行仿真

在深入探討GAM時，通過模擬數據來加深對其模型及其潛在局限性的理解變得尤為重要。特別是對于GAM，模擬過程涉及到線性預測器（或稱設計矩陣）的生成，這是通過將協變量映射到其對應的基函數上而得到的。

理解GAM模型中系數的含義

一個關鍵步驟是查看線性預測矩陣（我將其簡稱為(X_{lp})），這個矩陣對于理解GAM中的系數至關重要。在R中，使用mgcv包中的predict.gam()函數，并設置type = 'lpmatrix'，我們可以輕松地生成這個矩陣。無論是針對新數據還是擬合模型時使用的原始數據，這一操作都同樣適用。以下是如何針對原始數據生成線性預測矩陣的示例：

Xp <- predict(model_1, type = 'lpmatrix')
dim(Xp)

## [1] 84 28

您可以看到矩陣中有 84 行，對應于我們數據中的 84 個觀測值。但是我們有 28 列，其中許多列表示模型中兩個平滑項的基函數

這些對應于我們之前從擬合模型中提取的系數?

## [1] TRUE

如果我們使用線性代數將這些系數與設計矩陣 \（（X_{lp}\beta）\） 交叉相乘，我們會得到鏈接尺度上的預測值：

通過反向鏈接函數（在我們的對數鏈接的情況下）運行這些函數，為我們提供了模型中的擬合值exp()

## [1] TRUE

從模型的隱含多元正態后驗分布中抽取(\beta)系數來研究預測中的不確定性是一個高級話題，它涉及到貝葉斯統計和MCMC（馬爾可夫鏈蒙特卡洛）方法，這通常用于更復雜的模型評估。不過，對于大多數GAM（廣義加性模型）的常規應用，我們通常關注于點預測和預測區間，這些可以通過predict.gam()函數直接獲得，而無需顯式地抽取(\beta)系數的后驗樣本。

現在，讓我們聚焦于您提到的實際應用場景：當您向GAM模型提供新數據時，如何利用這些數據進行預測。假設您已經有一個擬合好的GAM模型，該模型研究了不同CO?濃度和溫度處理下植物的生長情況。現在，您想要預測在特定CO?濃度（如278 ppm）和特定處理（如未冷卻處理）下植物的某種響應（比如生長率）。

## [1]  1 28

在這里，我們采用了相對簡單的場景，并通過所有必要的基礎評估來生成設計矩陣。然后，從此方案生成預期值就像以下簡單方法一樣簡單：

exp(newXp %*% beta)

##       [,1]
## 1 27.56059

可能很難理解這種方法的力量，但一旦你掌握了這些步驟，探索目標場景的可能性是無窮無盡的。例如，我們可以使用這些步驟來查看效果的基礎基函數是什么樣子的。只需模擬一系列假值以覆蓋協變量的范圍，并通過函數運行這些值（將其他協變量固定到特定值）：

newXp <- predict(model_1, type = 'lpmatrix', newdata = newdat)

求哪些系數屬于conc

## [1] 17 18 19 20 21 22

現在將 \（X_{lp}\） 矩陣中與這些系數不對應的所有單元格設置為零

在鏈路尺度上生成預測并繪制函數

ggplot(plot_dat, aes(x = conc, y = value, col = basis_func)) +

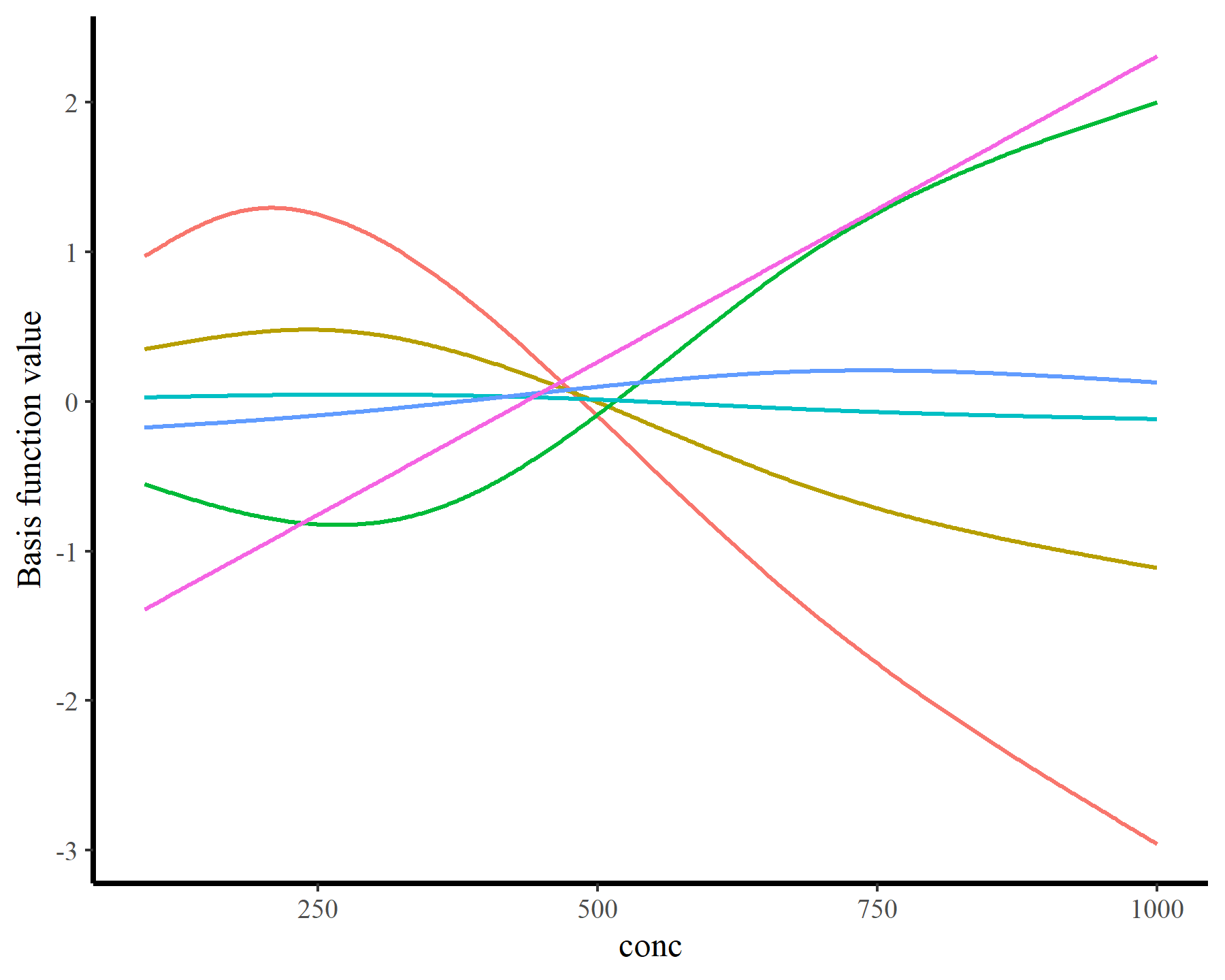
確實，當處理包含多個協變量的模型時，手動為所有感興趣的預測場景創建newdata數據框可能會變得既繁瑣又容易出錯。這就是為什么自動化工具在這種情況下變得極其有價值的原因。通過使用復雜的規則自動設置缺失預測變量的值，可以毫不費力地創建這些方案。

在這里，您會注意到只有目標變量在行與行之間變化，而其余所有變量均保持固定。為了探索并優化這些變量配置，您可利用預設的默認規則（及其自定義選項），這些規則旨在輔助解決潛在的預測挑戰。通過巧妙結合marginaleffects的datagrid函數與mgcv的predict.gam()功能（特別是當type = 'lpmatrix'時），您可以高效地利用虛擬數據來構建具有針對性的查詢。值得注意的是，在調用plot_predictions()、plot_slopes()或datagrid()等函數時，背后實際上自動調用了必要的邏輯以精確設置設計矩陣，比如conc等變量的處理。

值得一提的是，marginaleffects的強大之處不僅限于GAM，它提供了一個清晰、簡潔的框架來探索非線性效應，同時也廣泛兼容R中多種模型類（當前已支持超過100種），這一特性極大地促進了模型間的比較與分析。例如，即便是在處理包含復雜多項式交互效應的GLM（盡管這通常不是一個推薦的做法，僅為示例）時，marginaleffects也能游刃有余地助力您將模型擬合至相同數據集，進而深入洞察數據背后的故事。

我們可以從我們之前制作的 GAM 中重新制作濃度效應的圖之一

plot_predictions

我們可以生成完全相同的圖，但現在有了 GLM。請注意，除了 model 參數之外，調用 to 中的單個字符都不必更改plot_predictions()

plot_predictions(model_2

如何從我們的GAM模型中提煉出更為直接且深刻的問題呢？

第三步：深化GAM的比較分析

多數模型旨在描述而非直接模擬數據背后的因果機制。然而，這恰好賦予了我們利用回歸模型探索不同場景間差異、并詢問模型何為合理預測的能力。

差異平滑的奧秘：探索各組之間平滑效果的微妙變化

近期關于計算因子-平滑交互中平滑差異的研究，為我們深入理解{}在GAM比較中的強大作用提供了寶貴視角。當研究者希望擬合類似您之前探討的GAM（含因子-平滑交互），以洞察非線性效應如何隨因子水平變化時，問題雖看似簡單，但手動處理卻頗為棘手。幸運的是，{}提供了一系列專門設計的函數，極大地簡化了這一過程。這些函數能夠比較不同場景下的預測，無論是計算差異、比率，還是執行用戶自定義的函數（如轉換對數賠率或彈性），都游刃有余。

具體而言，我們可以通過整合uptake、type、conc和treatment等變量，計算處理間值的平均預期差異，從而得到一種‘全局’效應度量，該度量不受特定type或conc值的影響，是總結模型效果的有力工具。"

在這里，我們可以清晰地觀察到，在反應的尺度上，不同治療之間的平均差異顯著且強于某個特定的基準（盡管您在此處未明確提及該基準是什么，可能是指未治療組或另一種治療方式）。這種對比不僅提供了估計的效應大小，還附帶了相應的p值，以量化這種差異在統計上的顯著性。為了獲取這些詳細的結果，包括效應大小和p值，您可以使用marginaleffects包的comparisons函數，并通過指定type參數來進一步細分或定制比較的類型。

這為我們提供了兩個平滑值之間的預期差值。它非常有用，因為它已經考慮了截距的任何變化或模型中可能出現的其他影響。我們可以繪制這些差異：

我們還可以提出諸如非線性斜率增長最快的?conc?值等問題？這種問題在時間序列建模中非常有用，例如，如果我們想知道人口趨勢何時增長（或減少）最快。為函數提供自定義函數可以實現這一點：comparisons()

在這里，我們可以看到，對于這兩種處理，非線性效應的斜率似乎在conc = 155附近增長最快。

或者我們可以問：在什么 conc?值下，斜率與零有顯著差異？通過再次聚合和計算一系列值的一階導數，我們可以使用默認情況下詢問數量是否與零顯著不同的函數：

在深入探討科學報告中如何精準呈現GAM（廣義可加模型）的影響時，我們時常會遭遇需要細化假設的情境，而這些假設的設定往往能借助R來輕松實現。

如何在期刊中精準報告GAM的影響？

最終，我將聚焦于解答GAM領域的一個普遍疑問：如何有效地傳達這些復雜而精細的分析結果？以下是我提煉的幾點關鍵建議，旨在促進GAM非線性效應在科學交流中的準確傳達與深入理解，特別是借助marginaleffects等工具的輔助：

1. 超越p值與統計顯著性：應避免過分依賴p值作為效應存在與否的唯一標準。將連續變化的效應簡化為二元分類，往往會忽略大量寶貴的信息。相反，應關注效應的實際大小及其對結果預期變化的貢獻。

2. 聚焦效應對結果規模的影響：選擇GAM與GLM，正是為了捕捉現實世界中非高斯分布的復雜現象，這意味著鏈接函數常呈現非線性特性。因此，解釋效應時，應努力在線性預測變量的尺度上闡明其含義，盡管這可能對部分讀者構成挑戰。

3. 利用仿真增強理解：通過仿真手段，我們可以深入探究模型在不同情境下的合理預測范圍。這不僅有助于自身對模型行為的理解，也需在報告中詳盡描述仿真策略及其合理性依據，從而增強結論的可信度。

4. 對比不同模型以評估穩健性：將GAM與其他模型（如多項式回歸、線性模型）進行對比分析，是評估結論對函數形式選擇敏感性的重要步驟。這種跨模型的比較能夠揭示不同假設下結論的穩定性，為科學論斷提供更加堅實的支撐。

綜上所述，通過避免對p值的過度依賴、關注效應的實際影響、利用仿真深化理解以及進行跨模型比較，我們可以在期刊中更加全面、準確地報告GAM的非線性效應，促進科學知識的有效傳播與應用。