DPP能夠對目標檢測proposal進行非統一處理,根據proposal選擇不同復雜度的算子,加速整體推理過程。從實驗結果來看,效果非常不錯
來源:曉飛的算法工程筆記 公眾號
論文: Should All Proposals be Treated Equally in Object Detection?

- 論文地址:https://arxiv.org/abs/2207.03520
- 論文代碼:https://github.com/liyunsheng13/dpp
Introduction
? 在目標檢測中,影響速度的核心主要是密集的proposal設計。所以,Faster RCNN → Cascade RCNN → DETR → Sparse RCNN的演變都是為了稀疏化proposal密度。雖然Sparse R-CNN成功地將proposal數量從幾千個減少到幾百個,但更復雜deation head導致減少proposal數量帶來的整體計算收益有限。
? 復雜的deation head結構雖然能帶來準確率的提升,但會抹殺輕量級設計帶來的計算增益。對于僅有300個proposal的Sparse RCNN,deation head的計算量是主干網絡MobileNetV2的4倍(25 GFLOPS 與 5.5 GFLOPS)。
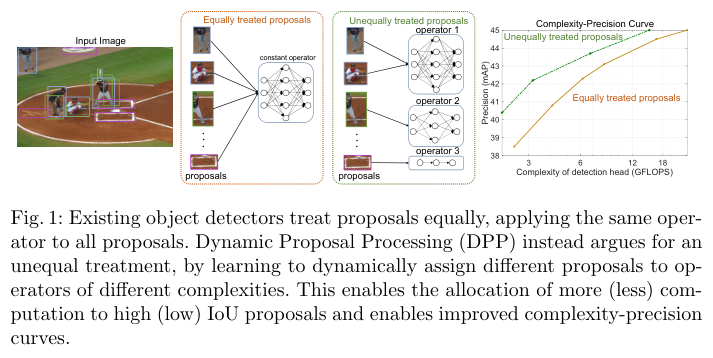
? 為此,作者研究是否有可能在降低deation head計算成本的同時保留精度增益和proposal稀疏性。現有檢測算法采用相同復雜度的操作處理所有proposal,在高質量proposal上花費大量的計算是合適的,但將相同的資源分配給低質量的proposal則是一種浪費。由于每個proposal的IoU在訓練期間是已知的,所以可以讓檢測器學習為不同的proposal分配不同的計算量。
? 由于在推理時沒有IoU,網絡需要學習如何根據proposal本身進行資源分配。為此,作者提出了dynamic proposal processing(DPP),將detection head使用的單一算子替換為一個包含不同復雜度算子的算子集,允許檢測器在復雜度-精度之間進行權衡。算子的選擇通過增加一個輕量級選擇模型來實現,該模型在網絡的每個階段選擇適用于每個proposal的最佳算子。
Complexity and Precision of Proposals
? 假設主干網絡產生了一組proposal X = { x 1 , x 2 , ? , x N } X = \{x_1, x_2, \cdots, x_N \} X={x1?,x2?,?,xN?},計算消耗主要來源于detection head而主干的計算消耗可忽略,并且將deation head的計算進一步分解為per-proposal的算子h(網絡結構)以及對應的proposal間處理組件p(NMS操作或proposal之間的的自注意機制)。
? 在之前的檢測器中,所有的proposal都由同一個算子h處理:
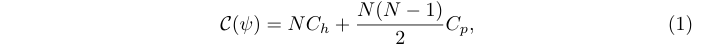
? 其中 ψ = { h , p } \psi = \{h, p\} ψ={h,p}, C h C_h Ch? 和 C p C_p Cp? 分別是h和p的 per-proposal 復雜度。
? 與其將相同的算子h應用于所有proposal,作者建議使用包含J個具有不同復雜度算子的算子集 G = { h j } j = 1 J \mathcal{G} = \{h_j\}^J_{j=1} G={hj?}j=1J?,由動態選擇器s選擇具體的算子分配給proposal x i x_i xi?:
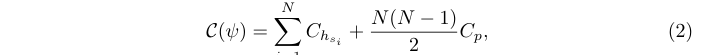
? 其中 s i = s ( x i ) s_i = s(x_i) si?=s(xi?), h s i ∈ G h_{s_i}\in \mathcal{G} hsi??∈G 表示來自 G \mathcal{G} G 的算子,由選擇器s分配給的proposal x i x_i xi?, ψ = { { h s i } i , s , p } \psi = \{\{h_{s_i}\}_i, s, p\} ψ={{hsi??}i?,s,p}, C h s i C_{h_{s_i}} Chsi???為整個per-proposal操作的計算復雜度。為簡單起見,p的復雜度仍然視為常數。
? 當deation head對proposal非統一處理時,給定復雜性約束C的最佳檢測器精度可以通過優化算子對proposal的分配來提升:
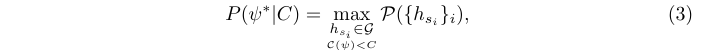
? 其中 P ( { h s i } i ) \mathcal{P}(\{h_{s_i}\}_i) P({hsi??}i?)是分配的特定運算符 { h s i } i \{h_{s_i}\}_i {hsi??}i?的精度。隨著C的變化, P ( ψ ? ∣ C ) P(\psi^{?}|C) P(ψ?∣C)構建了復雜度-精度(C-P)曲線,該曲線表示了可使用 G \mathcal{G} G實現的目標檢測器在成本和精度之間trade-off的最佳性能。
Dynamic Proposal Processing
? 基于上面的背景,作者提出了一個動態proposal處理(DPP)。假設detection head由多個階段( ψ = ? 1 ° ? ° ? K \psi = \phi_1 \circ \cdots \circ \phi_K ψ=?1?°?°?K?)依次處理proposal,每個階段 φ K \varphi_K φK?由選擇器s從 G \mathcal{G} G中選擇的運算符實現。為了最小化復雜性,選擇器每次只應用于階段子集 k ∈ K ? { 1 , ? , K } k \in K \subset \{1,\cdots,K\} k∈K?{1,?,K},其余階段使用上一次處理選擇的運算符,即 ? k = ? k ? 1 , ? k ? K \phi_k = \phi_{k?1}, \forall k\notin K ?k?=?k?1?,?k∈/K。
Operator Set
? 作者提出了由三個計算成本差異較大的算子組成的算子集合 G = { g 0 , g 1 , g 2 } \mathcal{G} = \{g_0, g_1, g_2\} G={g0?,g1?,g2?}:
- g 0 g_0 g0?是高復雜度的算子,由一個參數與proposal相關的動態卷積層(DyConv)和一個前饋網絡(FFN)來實現,類似于Sparse R-CNN采用的動態Head結構。
- g 1 g_1 g1?是一個中等復雜度的算子,由FFN實現。
- g 2 g_2 g2?是一個由identity block構建的輕量級算子,只是簡單地傳遞proposal而無需進一步提取特征。
Selector
? 在DPP中,通過控制操作符對proposal的分配,選擇器是控制精度和復雜性之間權衡的關鍵組件。定義 z i k z^k_i zik?是proposal x i x_i xi?在階段 ? k \phi_k ?k?的輸入特征,選擇器由3層MLP實現,輸出與關聯 z i k z^k_i zik?的3維向量 ? i k ∈ [ 0 , 1 ] 3 \epsilon^k_i \in [0, 1]^3 ?ik?∈[0,1]3:
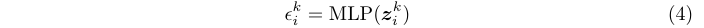
? 其中 ? i , j k \epsilon^k_{i,j} ?i,jk?是 ? i k \epsilon^k_i ?ik?中的選擇變量,代表將操作 g j g_j gj?分配給proposal x i x_i xi?的權重:
- 在訓練期間,選擇向量是包含三個變量one hot編碼,將Gumble-Softmax函數作為MLP的激活函數,用于生成選擇向量。
- 在推理中,選擇向量包含三個連續值,選擇值最大的變量對應的操作。
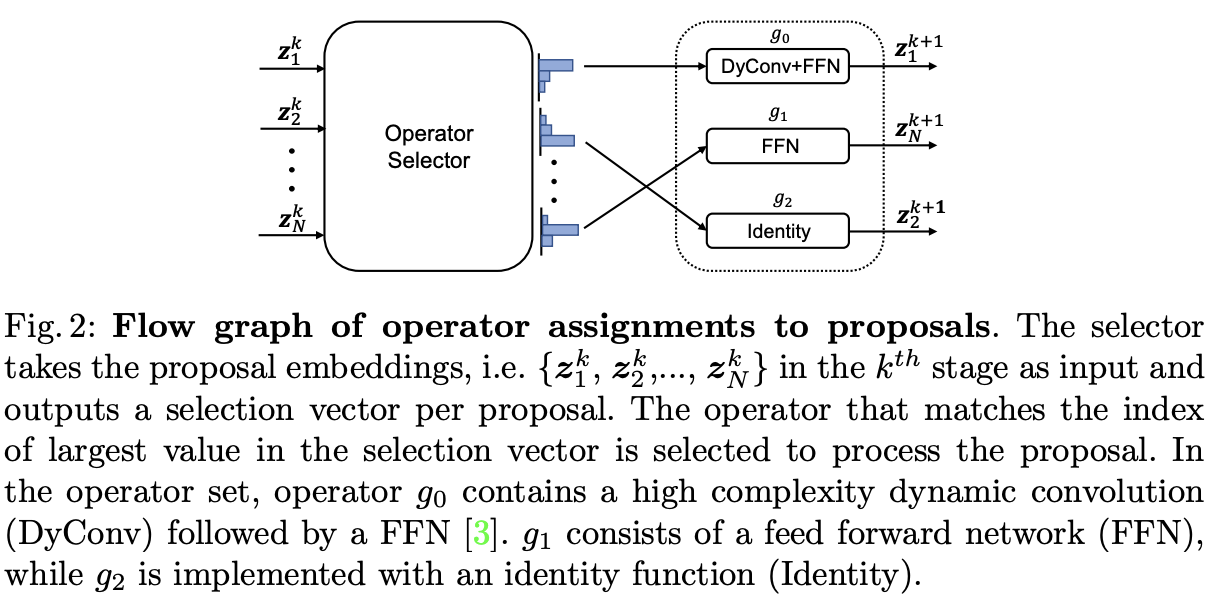
? 分配過程如圖2所示,整體開銷非常小(100個proposal僅需4e-3 GFLOPS),與detection head相比可以忽略不計。
? 從公式4可以看出,不同的proposal和階段選擇的算子都有變化,從而能夠進行動態處理。
此外,雖然 G \mathcal{G} G僅有三個候選項,但潛在的detection head網絡結構有 3 ∣ K ∣ 3^{|K|} 3∣K∣種。最后,由于選擇器是可訓練的,所以整體結構可以端到端學習。
Loss Functions
? 為了確保在給定復雜度的情況下,DPP能為每個proposal選擇最優的操作序列,作者增加了選擇器損失,包含兩個目標:
-
首先,應該將復雜的算子( g 0 g_0 g0?和 g 1 g_1 g1?)分配給高質量的proposal(高IoU):
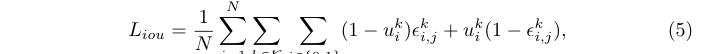
其中 u k u_k uk?是第i個proposal在第k階段的 IoU。當IoU小于0.5時, L i o u L_{iou} Liou?推動選擇器將 ? i , 0 k \epsilon^k_{i,0} ?i,0k?和 ? i , 1 k \epsilon^k_{i,1} ?i,1k?變為0,反之則變為1,鼓勵在階段 k 中使用更復雜的算子來獲得高質量的proposal。此外,損失的大小是由IoU值決定的,為高IoU proposal選擇簡單結構或為低IoU proposal選擇復雜結構均會產生大梯度值。 -
其次,選擇器應該知道每張圖像中的實例總數,并根據總數調整整體復雜度,在實例密集時選擇更復雜的算子:
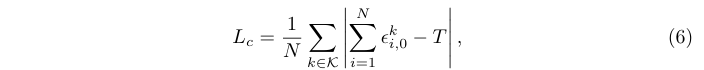
其中T是特定圖像選擇 g 0 g_0 g0?算子目標次數,定義為 T = α M T = \alpha M T=αM,即圖像中M個實例的倍數。此外, T ∈ [ T m i n , N ] T\in [T_{min}, N ] T∈[Tmin?,N]需通過根據預先指定的下限 T m i n T_{min} Tmin?和由總體proposal數N給出的上限對 α M \alpha M αM進行裁剪。下界防止對高復雜度算子進行過于稀疏的選擇,然后 α \alpha α則是根據實例數調整選擇器。
? 最終的整體選擇器損失為:
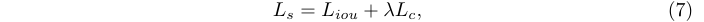
? 選擇器損失是一種即插即用損失,可以應用于不同的對象檢測器。在實現時,與應用DPP的原始檢測器的所有損失相結合,包括交叉熵損失和邊界框回歸損失。
Experiments
? DPP的主干網絡使用MobileNet V2或ResNet-50,使用特征金字塔網絡(FPN)生成多維特征,在其之上使用Sparse R-CNN的策略學習初始proposal。為簡單起見,選擇器僅應用于階段 K = { 2 , 4 , 6 } K = \{2, 4, 6\} K={2,4,6}。
? 對于損失函數,設置 λ = 1 \lambda=1 λ=1, T m i n = 1 T_{min}=1 Tmin?=1, α = 2 \alpha=2 α=2, N = 100 N=100 N=100。
Proposal processing by DPP
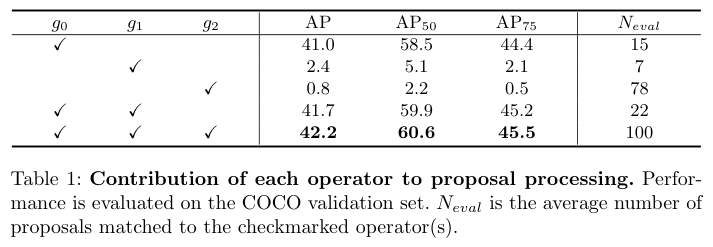
? 不同候選算子對性能的貢獻。
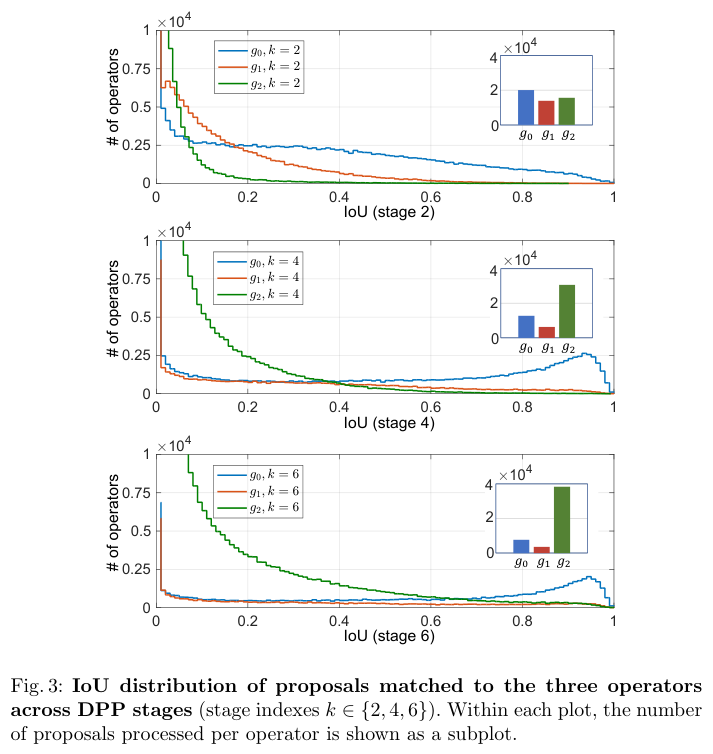
? 階段1~6的AP分別為 { 15.6 , 32.1 , 39.3 , 41.7 , 42.0 , 42.2 } \{15.6, 32.1, 39.3, 41.7, 42.0, 42.2\} {15.6,32.1,39.3,41.7,42.0,42.2},精度在前 4 個階段迅速增加,然后達到飽和。較后的階段,復雜算子占比越少,這說明 DPP 如何在復雜性與精度之間取得相當成功。

? 階段4和階段6中, g 0 g_0 g0?的預測結果。
Main Results
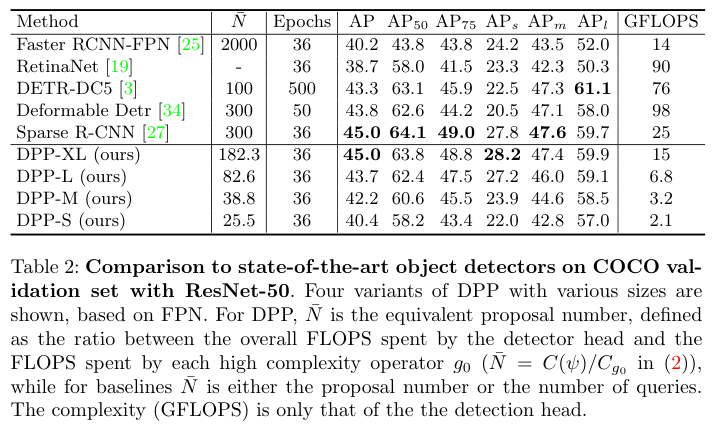
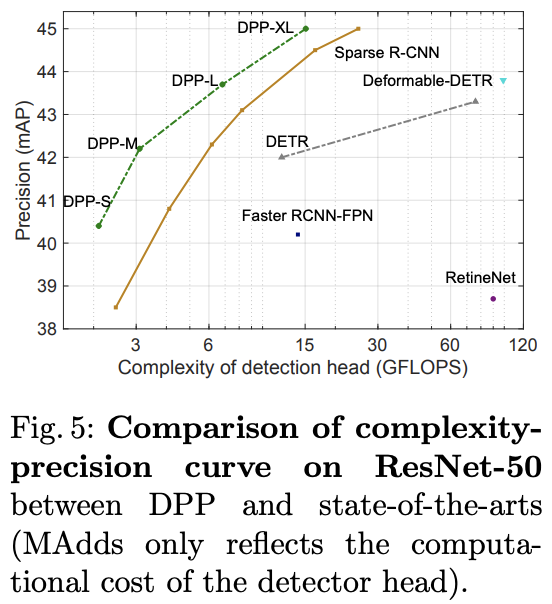
? 基于ResNet50與SOTA算法對比。

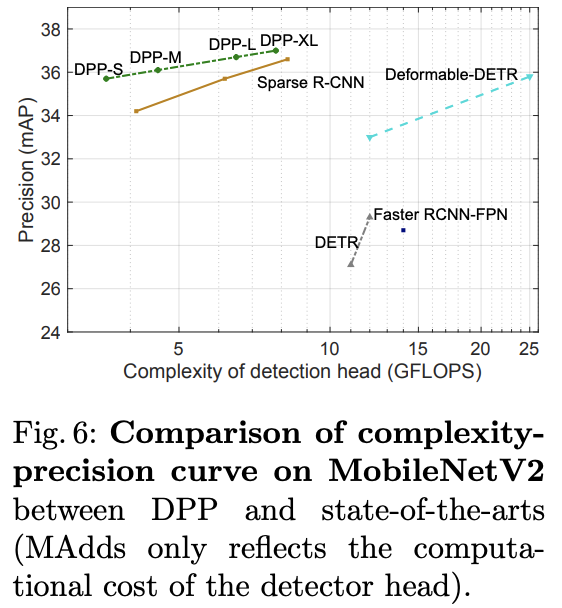
? 基于MobileNetV2與SOTA算法對比。
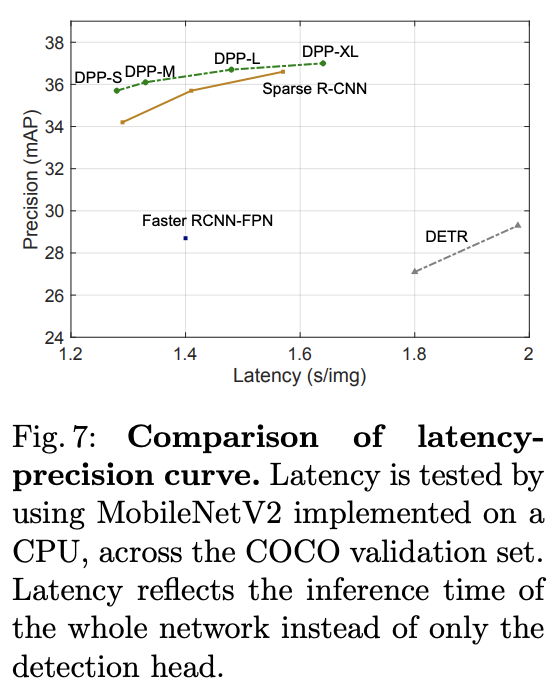
? 推理速度對比。
Ablation Study

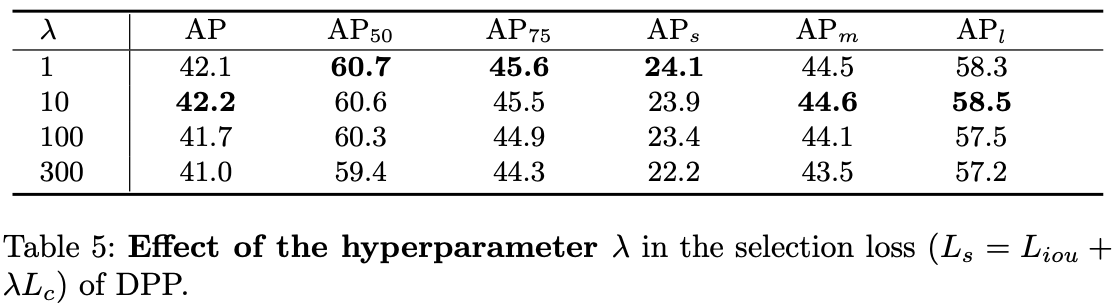
? 選擇器損失的作用。
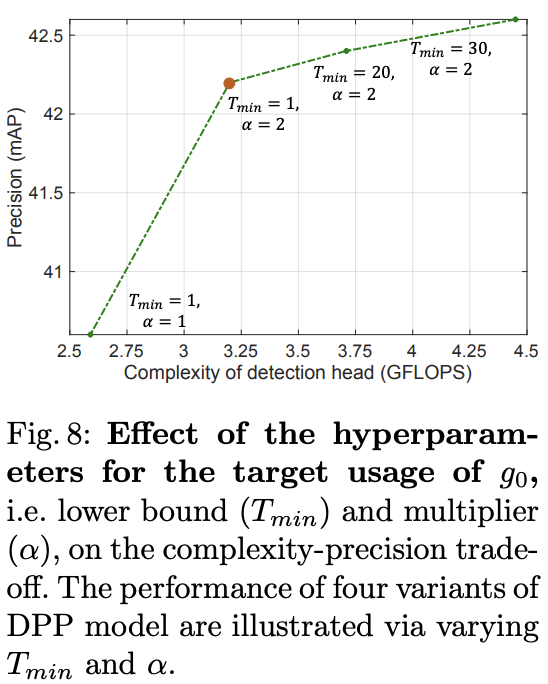
? 復雜算子預期數量的作用。
Conclusion
? DPP能夠對目標檢測proposal進行非統一處理,根據proposal選擇不同復雜度的算子,加速整體推理過程。從實驗結果來看,效果非常不錯。
?
?
?
如果本文對你有幫助,麻煩點個贊或在看唄~
更多內容請關注 微信公眾號【曉飛的算法工程筆記】










)




)
(更新中……))



