? ? ? ? 好了，今天我們來了解一下，我們在做練習題中常出現的一個名詞。時間復雜度。我相信大家如果有在練習過題目的話。對這個名詞應該都不陌生吧。但是可能很少的去思考它是干什么的代表的什么意思。反正我以前練習的時候就是這樣。我只知道有這么一個名詞在題目里面。但是這個限制的是什么我都不知道。因為在開始的簡單練習題中對時間復雜度的要求很低。大家用暴力求解法幾乎都可以。但是到后來很多方面都對這個是有要求的了。不再像以前那樣，暴力求解都可以解決問題的了。好，我們現在講這么多。都只是讓大家對時間復雜度稍微有一點了解。接下來我們就來詳細的介紹一下時間復雜度的含義以及如何計算時間復雜度。

時間復雜度的含義

? ? ? ?對于時間復雜度的含義的話我們先用官方的解釋來給大家過一遍：在計算機科學中，算法的時間復雜度是一個函數，它定量描述了該算法的運行時間。一 個算法執行所耗費的時間，從理論上說，是不能算出來的，只有你把你的程序放在機器上跑起來，才能知 道。但是我們需要每個算法都上機測試嗎？是可以都上機測試，但是這很麻煩，所以才有了時間復雜度這個 分析方式。一個算法所花費的時間與其中語句的執行次數成正比例，算法中的基本操作的執行次數，為算法 的時間復雜度。?這些都是比較官方的書法了我個人覺得這樣的解釋對于還不太了解時間復雜度的小白來說還是有點太深奧了。要是用我自己理解的白話來講的話，大家可以想象一下。一個簡單的循環。這個循環執行了多少次。然后這個次數就是我們的時間復雜度。我覺得這個解釋算是通俗易懂的了。

? ? ? ? 當然如果所有的時間復雜度都是看一個循環就能得出來的話那就太簡單了。我們后面接觸的需要考慮時間復雜化度的時候就有很多元素了。在開始的時候大家甚至都可以帶一個值進去估算一下。有個大概結果。并且我們的時間復雜度確實不用那么準確。

舉例解釋時間復雜度

? ? ? ?如果我們光講的話，對時間復雜度的了解肯定是不夠的。所以我們還是舉一些例子來幫助大家理解。當然是從簡單到難得。

? ? ? ?大家可以先來看一下這個比較簡單的時間復雜度計算題。如果你覺得不能一眼看出來時間復雜度并且還是在前期的時候我們就帶值進去計算一下。比如說我們上面我們給的例題，我們先帶一個10.然后計算看值是多少？然后再帶100,1000分別計算一下。

? ? ? ? 這里我已經提前計算過來。大家如果感興趣的話可以自己再去驗算一遍。但是啊。大家看。這里我們雖然計算出來了?F(N)的大小，但是大家應該發現了吧。我們平常見到的時間復雜度都是一些什么O（）什么什么的吧。是吧。那我們如果照著這樣寫的話，是不是就很不合大眾啊。那么我們也要學習如何用這個大O來表示時間復雜度吧。

大O表示法

? ? ? ? 對于大O表示法來說咧。我們先來看看正式的解釋：是用于描述函數漸進行為的數學符號。出了算法的速度有多快。當然是趨向于操作的次數，因為每種操作的方式不同所需的時間也就無法統一。大O表示法通常作為一個算法優劣的標準，越快越好，數值越小越快。對于官方解釋哈。我反正是基本聽不懂的。但是有人能聽懂啊。所以他們給我講的時候是這樣說的括號里面的取這個公式里面對這個公式影響最大的那個。怎么說咧。例如上面的例子F（N）=N*N+2*N+10。大家可以稍微思考一下這個公式里面對于結果誰的影響是最大的。是不是N*N啊。就是N的平法嘛。因為我不知道怎么打出一模一樣的，所以就這樣，意思是一樣的。好。大家可以理解一下。我們這里是不是n的平方在這個式子里面的影響力最大的。那么我們的大O表示法如何表示咧：O（N*N）。

? ? ? ?當然這個式子是固定的但是還有很多式子是無法確定的啊。例如在一個數組里面找一個數這個數一定在數組里面，那么這個式子的時間復雜度如何計算啊。最好情況：1次找到，最壞情況：N次找到，平均情況：N/2次找到。那么這個式子的時間復雜度如何寫咧。所以這里我們就引出了大O表示法的另一個規則，我們取最壞的結果。大家都聽過一句話，就是要做好最壞的打算。那么這里也是。我們大O表示法也是取最壞的。那么我們這個例子的時間復雜度就為O（N）。

? ? ? ?當然有些時候，像上面這個例子直接給我們說了N是多少，比如說m=10，while（m--）。那么我們這里的時間復雜度就是是O（1）了。為什么是O（1）咧。因為我們大O表示法明確表示過。對于N為明確的數值的時候都用1。表示這樣表示這個式子的計算速度就是最快的了。因為最壞的情況我們都能一眼看出來，那么這個循環或者遞歸都應該不是很難了。

? ? ? 當然還有很多的時間復雜度表示方法，這里我就以我們上面講過的幾大排序方法來舉例：

? ? ? ? 我們后面就會很少遇見O（1）的時間復雜化度了。所以，大家可以先看一下大致有哪些時間復雜度的表示方法。

兩個循環計算時間復雜度

? ? ? ? 這里咧我們就不講單個時間復雜度是如何計算的了。因為如果沒有明確的寫出循環的個數的話。大多都是O（N）。所以我們這里直接來講講雙循環是如何計算的。

? ? ? ? 對與這樣簡單的分開的兩個循環來計算時間復雜度的來說。我們可以分開來看第一個循環是不是關鍵再與M。然后第二個循環關鍵在于N。然后我們計算的是++count執行了多少次。那么我們是不是就最好的情況是1+1。兩個循環都是一次就結束了。但是最壞的咧。是不是每次都執行完了。那就是M+N了。我們前面也說過取最壞的情況。那么這里我們的時間復雜度是不是就是O（M+N）了。

strchr計算時間復雜度

? ? ? ? 大家對于strchr的作用應該還沒忘吧。就是在一個字符竄里面尋找一個字符。就是我們前面說過的簡單的單循環計算。

? ? ? ?既然是簡單的單循環計算了，那么時間復雜度也是簡單的O（N）了吧。

冒泡排序計算時間復雜度

? ? ? 冒泡排序大家肯定都沒忘吧。畢竟大家還是小白的時候應該都寫過這個吧。接下來我們就是來嘗試計算一下冒泡排序的時間復雜度。

? ? ? ?我們來看看冒泡排序最好的情況就是執行n次就結束了。但是最壞的情況就是內部不是有序數列，那么就?當end=n-1的時候內部就要執行n-2次。當end=n-2的時候內部就要執行n-3次....當end=2時，內部就執行1次end=1時內部執行0次。end不能為0。那么這個循環是不是就是（1+n-1）*n/2然后我們整合一下就是（n*2）/2。那么最壞的情況下，影響最大的就是n*2了。那么冒泡排序的大O表示法就是O（n*2）。大家應該明白吧。就是稍微帶值進去計算得出個大概規律。我們不需要十分準確，有個大概就是可以了。如果太精確也沒啥意義其實。

遞歸計算時間復雜度

? ? ? ? 講了上面幾個例子接下里我們講講另外一個常見的計算時間復雜度的。遞歸。這個也是我們前期學過的了。那么遞歸的時間復雜度如何計算咧。

? ? ? ?這個遞歸是很簡單的。我們只需要康康n就可以了。也可能一次就結束了，也有可能要n次。那么老規矩取最壞的情況。我們就取n。所以這個遞歸的時間復雜度為O(N)。

遞歸斐波拉契數計算時間復雜度

? ? ? 遞歸斐波拉契數的這個難度可就不是上面的那些簡單就能想出來的了哦。我們建議計算這個最好是畫一畫圖遞歸棧幀的二叉樹講解。反正已經學過二叉樹了。我們就用起來然后幫助理解。

斐波那契數列是這樣一個數列：1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765…

表達式為：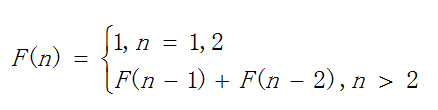

?

? ? ? ? 對于Fib(5)的遞歸過程可知，執行次數最多不超過但接近于二叉樹最多時候的節點數，可近似看為2 n ? 1 2^n-12?n??1，所以時間復雜度T(n)為2 n 2^n2?n的同階，即T ( n ) = O ( 2 n )? ? ? ? ? ? ? ? ? ? ? ?T(n)=O(2^n)T(n)=O(2?n?)在遞歸調用的過程中，除了存放程序本身所用的指令和變量，還需要另外開辟n個變量來作為輔助空間，分別對應Fib(n-1)，Fib(n-2)，Fib(n-3)，…，Fib(0)中的n-1，n-2，n-3，…，0。因此，空間復雜度為O (n)。?

總結

? ? ? 好了，當大家看到這里我想應該就對計算時間復雜度有一些了解了吧。反正我一直用的都是帶幾個值進去計算一下。然后就可以得出一個大概的邏輯這樣得出一個大概的就可以了。那么今天的時間復雜度計算就到這里了。下一篇我們會分享一下空間復雜度的計算。