R語言數據分析案例42-基于時間序列模型對股票預測分析和研究

一、研究背景和意義

隨著全球經濟的不斷發展和數字化轉型的加速推進，科技公司在全球市場中扮演著日益重要的角色。其中，中國的阿里巴巴集團作為全球最大的電子商務公司之一，其業務范圍覆蓋電子商務、云計算、金融科技等多個領域。由于其在中國及全球市場的影響力和市值巨大，阿里巴巴的股票價格不僅關乎公司自身的發展狀況，也反映了中國和全球經濟的整體走勢。股票價格是金融市場最直觀、最重要的指標之一，對于投資者、分析師和政策制定者來說，了解和預測股票價格的波動具有重要的意義。時間序列分析作為一種經典的統計方法，可以幫助我們深入理解阿里巴巴股票價格的走勢規律，為投資決策和風險管理提供可靠的依據。。。。

二、研究綜述

在國內研究方面，翁紫霞為提供可參考的投資建議，提高投資者在股票市場的收益，基于建設銀行 2019 年 1 月 2 日—2022 年11 月 14 日每個交易日共計 939 組收盤價數據，應用 ARIMA 模型對股價進行預測和分析。結果顯示，應用 ARIMA 模型可對短期內股價進行很好的預測，但因股票市場受多種多重因素的影響，進行長期預測時可能存在較大誤差，需要深入探索更為準確的股價預測模型[1]。。。。姚金海通過構建一個基于ARIMA與信息粒化SVR的組合預測模型，對股票市場指數價格和收益變化的趨勢進行預測。實證研究結果表明：基于ARIMA與信息粒化SVR組合的股指預測模型相較于傳統時間序列模型而言，在預測精度和效度方面有較大提升，能夠在一定時間周期內對股票等風險資產的價格波動區間進行較為可靠地預測[7]。。。。

三、理論部分

ARIMA模型為自回歸移動平均模型，這是一個當選取的序列是非平穩序列時，能夠通過差分、季節分解等一系列方法后將該序列變為平穩序列，隨后繼續建模的一個模型

指數平滑法是一種常用于時間序列預測的簡單但有效的方法之一。它的核心思想是利用過去觀測值的加權平均來預測未來的值，其中過去觀測值的權重隨時間指數級衰減。

季節性自回歸整合移動平均模型（Seasonal Autoregressive Integrated Moving Average，sARIMA）是一種用于處理具有季節性的時間序列數據的方法。它是ARIMA模型的擴展，專門設計用于捕捉數據中的季節性變化。。。。

四、實證分析

本研究使用的數據來自阿里巴巴（股票代碼：SW9988）的股票市場交易數據，涵蓋了從 2022 年 1 月 1 日到 2024 年 3 月 12 日的時間范圍。這段時間內的交易數據記錄了阿里巴巴股票在市場中的各種表現和變化。

數據和代碼

報告代碼數據

首先讀取數據并且查看數據和其特征格式：

library(ggplot2)
library(vars)
library(readxl)
# 導入所需的庫
library(readr)
# 讀取CSV文件
data <- read_csv('C:/Users/DWW/Desktop/ALBB-SW9988.csv')
data
# 顯示數據的前幾行
head(data)

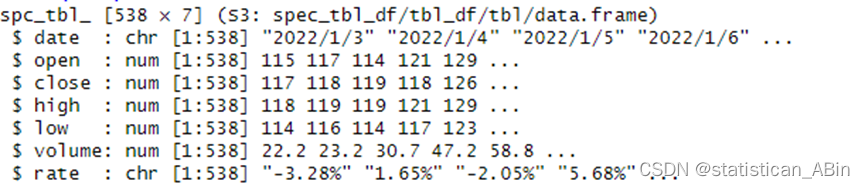?從上圖可以看見，其中包含了538個數據點，每個數據點有7個變量，主要是數值型和字符串形式。接下來轉換日期格式并且畫出時間序列圖：

data$date
# 繪制時間序列圖
ggplot(data, aes(x = data$date, y = ts_data)) +geom_line() +labs(x = "日期", y = "收盤價") +ggtitle("收盤價時間序列") +theme_minimal() +theme(plot.title = element_text(hjust = 0.5))

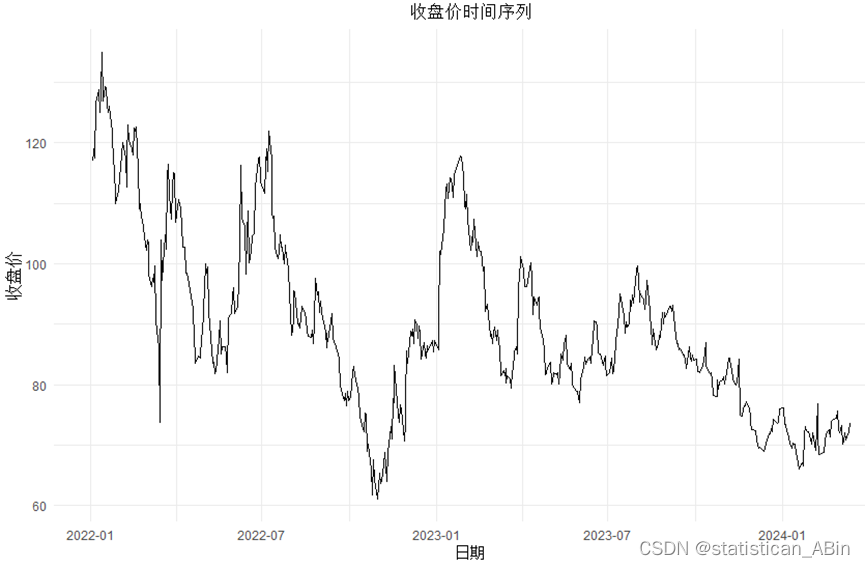
從圖中可以看出幾個特點，在波動性上，股票價格波動非常顯著，其中在2022年中到2023年初出現較大的波峰和波谷，這意味著在這段時間內股票價格的波動幅度較大。

接下來進行平穩性檢驗

拒絕了原假設，這意味著我們有足夠的證據來支持備擇假設，即時間序列數據是平穩的。接下來畫出ACF和PACF圖。

# 繪制ACF圖
acf(ts_data, main = "ACF Plot for ts_data")
# 繪制PACF圖
pacf(ts_data, main = "PACF Plot for ts_data")

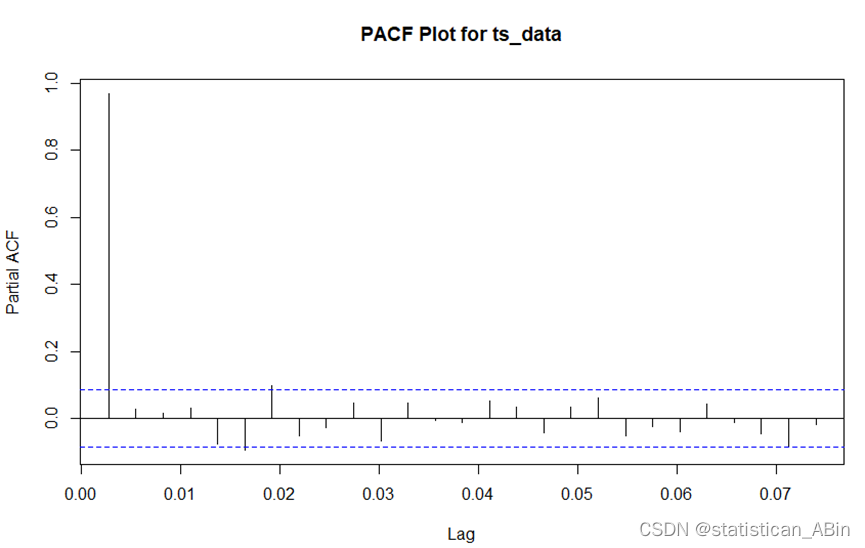?ACF圖顯示了時間序列與其自身過去值的相關程度。這幅圖顯示了在多個時間滯后（Lag）下，ACF值逐漸減小。在這里，幾乎所有的ACF條都是正值，并且逐漸減小到零，這通常是一個非平穩時間序列的指標。

在這里我們選取了arima (2, 0, 1)和自動定階的模型來比較，模型信息如下：

# 擬合模型
manual_arima_model <- arima(ts_data, order = c(2, 0, 1))
# 顯示手動選擇的ARIMA模型信息
print(manual_arima_model)
# 模型評價
accuracy(manual_arima_model)

模型參數：ARIMA(0,1,0)表示你選擇了一個差分階數為1的一階差分自回歸移動平均模型。這個模型沒有自回歸項（AR）和移動平均項（MA），只有一個一階差分（差分階數為1）。

ARIMA(2,0,1)模型的參數為：ar1 = 1.3046, ar2 = -0.3185, ma1 = -0.3804，同時還有一個截距項(intercept)為90.3917。參數的標準誤差分別為：ar1的標準誤差為0.4346，ar2的標準誤差為0.4245，，，

綜合來看，雖然ARIMA(2,0,1)模型在參數較多的情況下擬合了數據。可以通過圖來直觀比較兩模型的誤差：

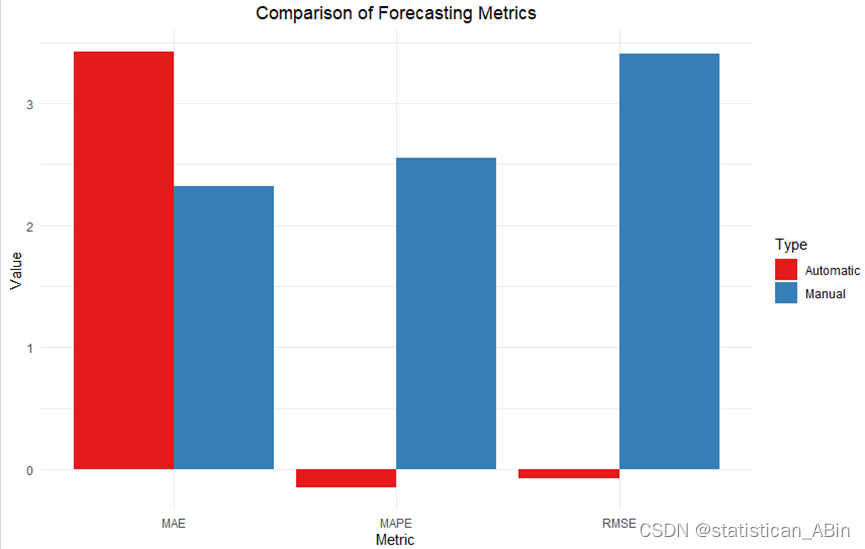
在MAE指標上，手動定階的模型性能低于自動定階模型，但是在RMSE和MAPE指標上，手動定階的模型性能顯著優于自動定階模型，

接下來展示一下ARIMA(2,0,1)的預測結果：

# 繪制圖表
ggplot(combined_data, aes(x=Date, y=Value, color=Data)) +geom_line() +labs(title="Time Series Forecast", x="Date", y="Closing Price") +theme_minimal()+theme(plot.title = element_text(hjust = 0.5))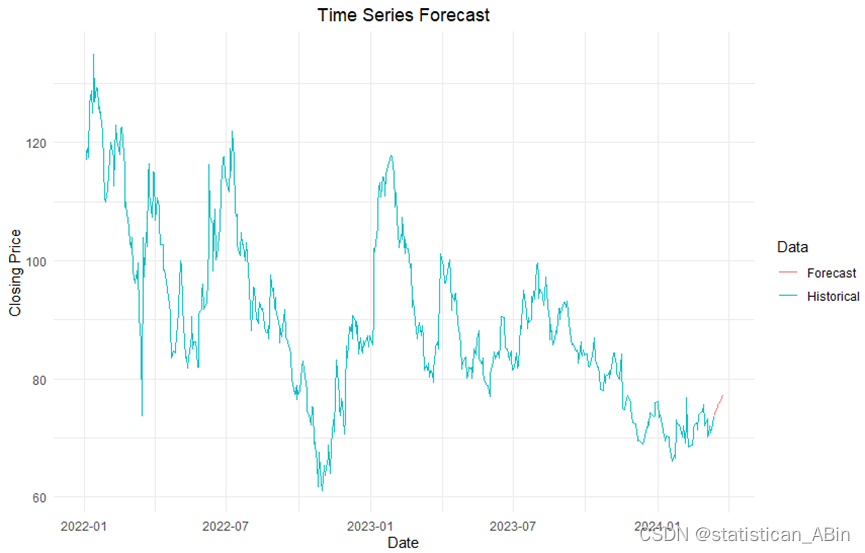

其中，藍色線顯示了2022年1月至2023年底的價格走勢。可以看到價格有明顯的波動，其中有幾個尖峰和深谷，這表明了該期間內的高波動性。。。。

接下來對模型進行殘差分析：

# 殘差分析
checkresiduals(manual_arima_model)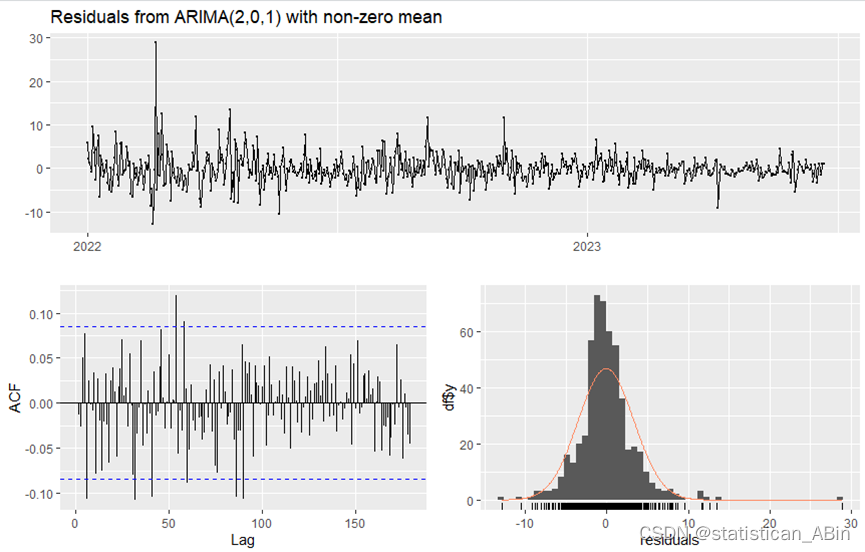

綜合這些圖表，我們可以得出結論，ARIMA(2,0,1)模型對數據進行了相對合理的擬合。

ETS模型

從上面結果可以得到，Smoothing parameters（平滑參數），alpha = 0.9422，這是平滑參數，它控制著對觀察值的權重。較高的alpha值意味著更多的權重被分配給最近的觀察值，。。

accuracy_ets <- accuracy(forecast_ets)
accuracy_ets
# 查看預測結果
plot(forecast_ets)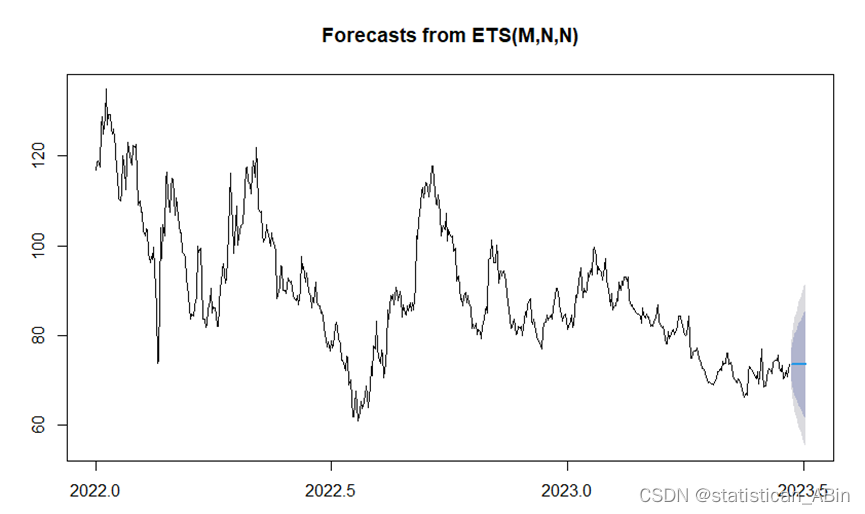

數據顯示了顯著的波動性和一個整體的下降趨勢。從大約2023年初開始，圖表以灰色區域顯示了12個時間周期的預測。。。。

?Prophet模型

接下來使用Prophet模型來對數據做12期的預測：

# 構建未來數據框架
future <- make_future_dataframe(m, periods=12, freq = 'day')
# 進行預測
forecast_prophet <- predict(m, future)
forecast_prophet
# 查看預測結果
plot(m, forecast_prophet)
prophet_plot_components(m, forecast_prophet)

Prophet是Facebook開發的一個開源工具，它適用于時間序列數據的預測，特別是對于具有強季節性模式和多個季節性周期的數據。?特別的，該模型的指標情況為：MAE為5.2771，RMSE:為6.7873，MAPE: 0.0612。

SARIMA模型以及混合模型ARIMA-ETS

首先看一下SARIMA模型

fit_sarima <- auto.arima(data_ts, seasonal=TRUE)
# 概覽模型
summary(fit_sarima)
# 進行預測
forecast_sarima <- forecast(fit_sarima, h=12)
# 查看預測結果
plot(forecast_prophet)

從上述模型參數可以知道，每個參數的標準誤差（s.e.）分別為：ar1的標準誤差為0.0686，ar2的標準誤差為0.0658，。。

接下來進行混合模型的預測實驗：

# 可視化預測結果
plot(forecast_arima, col="blue")
lines(forecast_ets$mean, col="red")
lines(combined_forecast, col="green")
legend("topright", legend=c("ARIMA", "ETS", "Combined"), col=c("blue", "red", "green"), lty=1)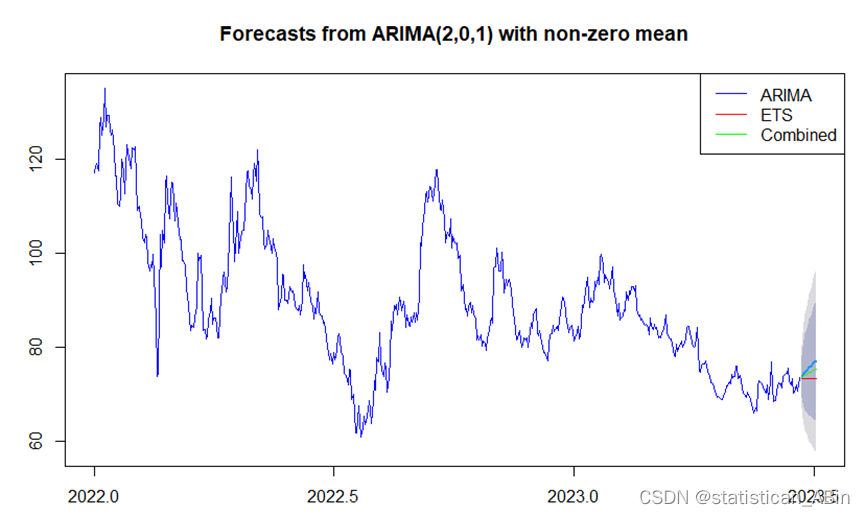

從上圖可以看出，ETS的預測是一條直線，說明預測未來股價會一直平穩，但是這可能性很小，從混合模型ARIMA-ETS和ARIMA模型對比來看，并不是模型通過混合之后其預測效果會變得更好，反之，有可能不如單一的時間序列模型。

五、結論和政策建議

在建模方面，我們嘗試了多種時間序列模型，包括ARIMA、ETS、Prophet和SARIMA等。經過比較，我們發現ARIMA(2,0,1)模型在擬合數據和預測效果上表現較好，具有較低的預測誤差和較高的擬合優度指標。。。。

參考文獻

翁紫霞.基于ARIMA模型的股價分析與預測——以建設銀行為例[J].現代信息科技,2023,7(14):137-141.DOI:10.19850/j.cnki.2096-4706.2023.14.029.
萬文娣. 機器學習在股票價格混合預測模型中的研究與應用[D].西北師范大學,2023.DOI:10.27410/d.cnki.gxbfu.2023.002345.
劉祺,施三支,婁磊等.基于ARIAM-GARCH深度學習的股價預測與決策[J].長春理工大學學報(自然科學版),2024,47(01):119-130.、

創作不易，希望大家多點贊關注評論！！！（類似代碼或報告定制可以私信）