本題為單源有限最短路問題，同樣是 kama94.城市間貨物運輸I 延伸題目。

注意題目中描述是 最多經過 k 個城市的條件下，而不是一定經過k個城市，也可以經過的城市數量比k小，但要最短的路徑。

在 kama94.城市間貨物運輸I 中我們講了：對所有邊松弛一次，相當于計算 起點到達 與起點一條邊相連的節點 的最短距離。

節點數量為n，起點到終點，最多是 n-1 條邊相連。 那么對所有邊松弛 n-1 次 就一定能得到 起點到達 終點的最短距離。

（如果對以上講解看不懂，建議詳看 kama94.城市間貨物運輸I ）

本題是最多經過 k 個城市， 那么是 k + 1條邊相連的節點。 這里可能有錄友想不懂為什么是k + 1，來看這個圖：

??

圖中，節點2 最多已經經過2個節點 到達節點4，那么中間是有多少條邊呢，是 3 條邊對吧。

所以本題就是求：起點最多經過k + 1 條邊到達終點的最短距離。

對所有邊松弛一次，相當于計算 起點到達 與起點一條邊相連的節點 的最短距離，那么對所有邊松弛 k + 1次，就是求 起點到達 與起點k + 1條邊相連的節點的 最短距離。

注意： 本題是 kama94.城市間貨物運輸I 的拓展題，如果對 bellman_ford 沒有深入了解，強烈建議先看 kama94.城市間貨物運輸I 再做本題。

理解以上內容，其實本題代碼就很容易了，bellman_ford 標準寫法是松弛 n-1 次，本題就松弛 k + 1次就好。

此時我們可以寫出如下代碼：

// 版本一
#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;int main() {
int src, dst,k ,p1, p2, val ,m , n;cin >> n >> m;vector<vector<int>> grid;for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，權值為 val
grid.push_back({p1, p2, val});
}cin >> src >> dst >> k;vector<int> minDist(n + 1 , INT_MAX);
minDist[src] = 0;
for (int i = 1; i <= k + 1; i++) { // 對所有邊松弛 k + 1次
for (vector<int> &side : grid) {
int from = side[0];
int to = side[1];
int price = side[2];
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) minDist[to] = minDist[from] + price;
}}if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到達終點
else cout << minDist[dst] << endl; // 到達終點最短路徑}

以上代碼 標準 bellman_ford 寫法，松弛 k + 1次，看上去沒什么問題。

但大家提交后，居然沒通過！

這是為什么呢？

接下來我們拿這組數據來舉例：

4 4
1 2 -1
2 3 1
3 1 -1
3 4 1
1 4 3

（注意上面的示例是有負權回路的，只有帶負權回路的圖才能說明問題）

負權回路是指一條道路的總權值為負，這樣的回路使得通過反復經過回路中的道路，理論上可以無限地減少總成本或無限地增加總收益。

正常來說，這組數據輸出應該是 1，但以上代碼輸出的是 -2。

在講解原因的時候，強烈建議大家，先把 minDist數組打印出來，看看minDist數組是不是按照自己的想法變化的，這樣更容易理解我接下來的講解內容。 （一定要動手，實踐出真實，腦洞模擬不靠譜）

打印的代碼可以是這樣：

#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;int main() {
int src, dst,k ,p1, p2, val ,m , n;cin >> n >> m;vector<vector<int>> grid;for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，權值為 val
grid.push_back({p1, p2, val});
}cin >> src >> dst >> k;vector<int> minDist(n + 1 , INT_MAX);
minDist[src] = 0;
for (int i = 1; i <= k + 1; i++) { // 對所有邊松弛 k + 1次
for (vector<int> &side : grid) {
int from = side[0];
int to = side[1];
int price = side[2];
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) minDist[to] = minDist[from] + price;
}
// 打印 minDist 數組 
for (int j = 1; j <= n; j++) cout << minDist[j] << " ";
cout << endl;}if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到達終點
else cout << minDist[dst] << endl; // 到達終點最短路徑}

接下來，我按照上面的示例帶大家 畫圖舉例 對所有邊松弛一次 的效果圖。

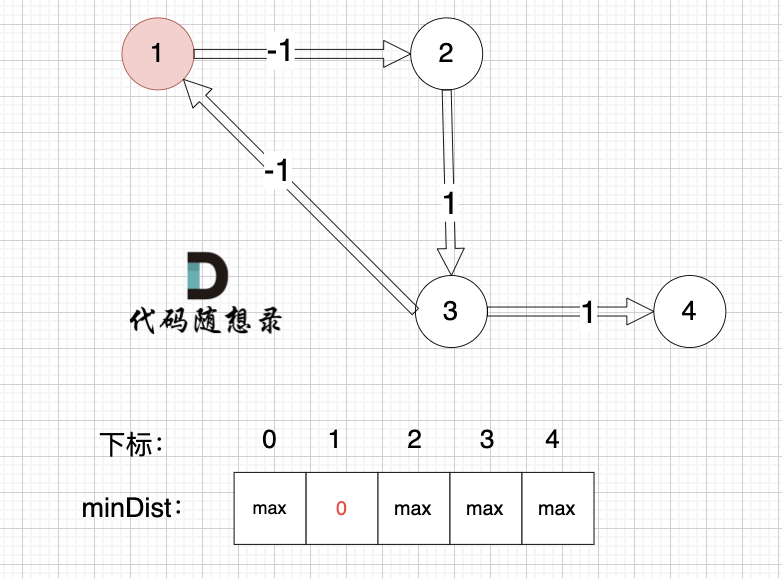
起點為節點1， 起點到起點的距離為0，所以 minDist[1] 初始化為0 ，如圖：

??

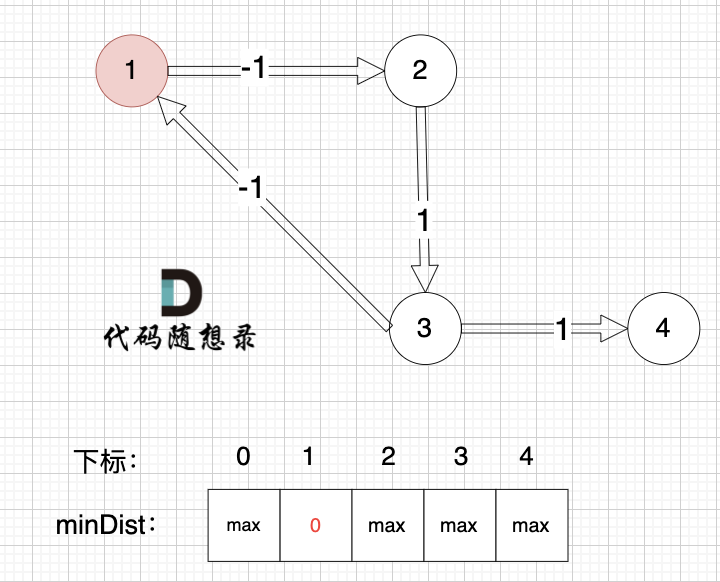其他節點對應的minDist初始化為max，因為我們要求最小距離，那么還沒有計算過的節點 默認是一個最大數，這樣才能更新最小距離。

當我們開始對所有邊開始第一次松弛：

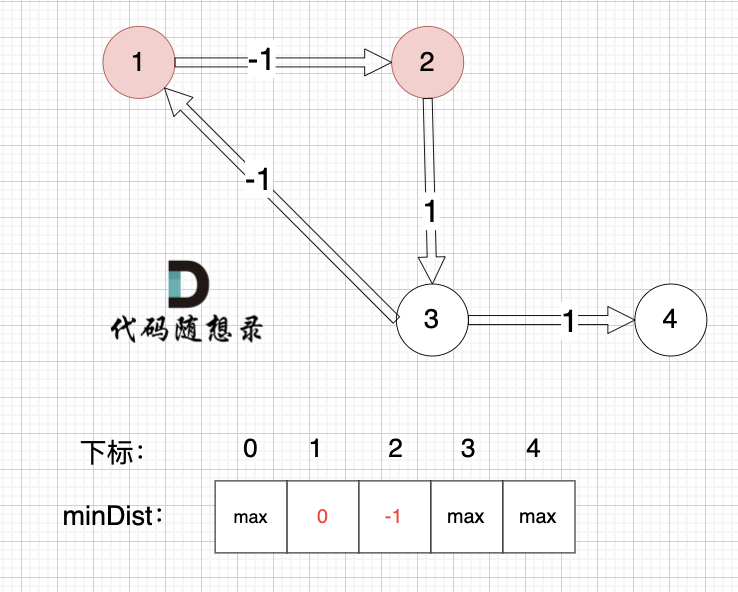
邊：節點1 -> 節點2，權值為-1 ，minDist[2] > minDist[1] + (-1)，更新 minDist[2] = minDist[1] + (-1) = 0 - 1 = -1 ，如圖：

??

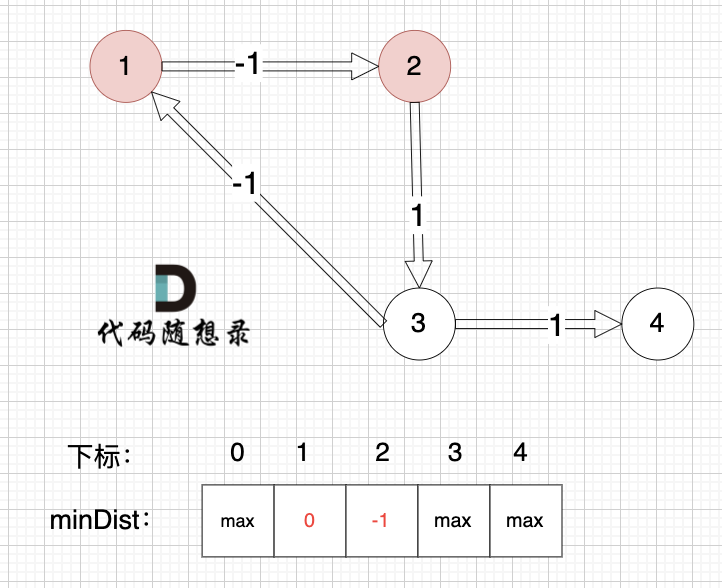邊：節點2 -> 節點3，權值為1 ，minDist[3] > minDist[2] + 1 ，更新 minDist[3] = minDist[2] + 1 = -1 + 1 = 0 ，如圖： ?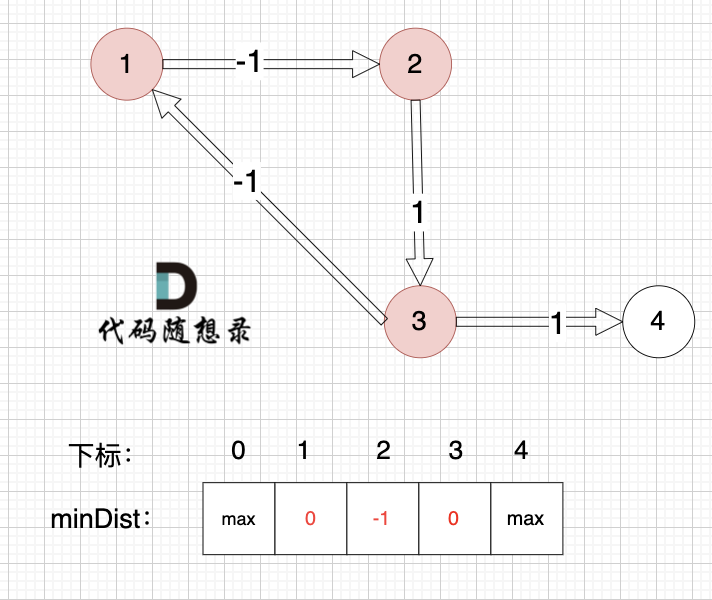

邊：節點3 -> 節點1，權值為-1 ，minDist[1] > minDist[3] + (-1)，更新 minDist[1] = 0 + (-1) = -1 ，如圖：

??

邊：節點3 -> 節點4，權值為1 ，minDist[4] > minDist[3] + 1，更新 minDist[4] = 0 + (-1) = -1 ，如圖：

??

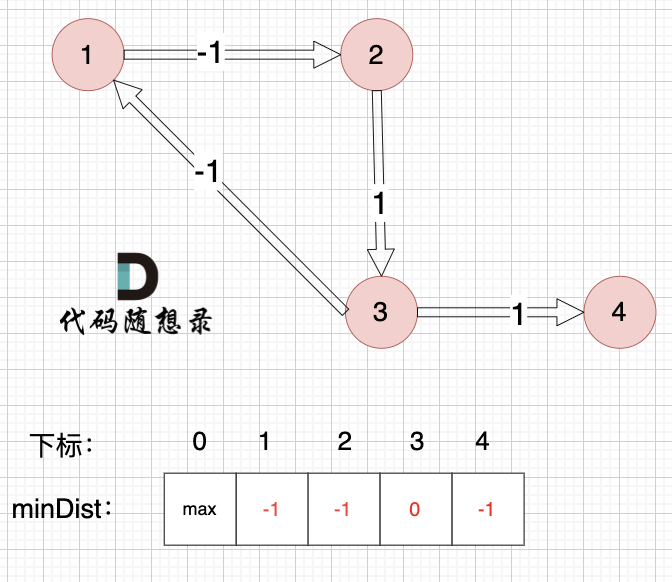以上是對所有邊進行的第一次松弛，最后 minDist數組為 ：-1 -1 0 1 ，（從下標1算起）

后面幾次松弛我就不挨個畫圖了，過程大同小異，我直接給出minDist數組的變化：

所有邊進行的第二次松弛，minDist數組為 ： -2 -2 -1 0 所有邊進行的第三次松弛，minDist數組為 ： -3 -3 -2 -1 所有邊進行的第四次松弛，minDist數組為 ： -4 -4 -3 -2 （本示例中k為3，所以松弛4次）

最后計算的結果minDist[4] = -2，即 起點到 節點4，最多經過 3 個節點的最短距離是 -2，但 正確的結果應該是 1，即路徑：節點1 -> 節點2 -> 節點3 -> 節點4。

理論上來說，對所有邊松弛一次，相當于計算 起點到達 與起點一條邊相連的節點 的最短距離。

對所有邊松弛兩次，相當于計算 起點到達 與起點兩條邊相連的節點的最短距離。

對所有邊松弛三次，以此類推。

但在對所有邊松弛第一次的過程中，大家會發現，不僅僅 與起點一條邊相連的節點更新了，所有節點都更新了。

而且對所有邊的后面幾次松弛，同樣是更新了所有的節點，說明 至多經過k 個節點 這個限制 根本沒有限制住，每個節點的數值都被更新了。

這是為什么？

在上面畫圖距離中，對所有邊進行第一次松弛，在計算 邊（節點2 -> 節點3） 的時候，更新了 節點3。

??

理論上來說節點3 應該在對所有邊第二次松弛的時候才更新。 這因為當時是基于已經計算好的 節點2（minDist[2]）來做計算了。

minDist[2]在計算邊：（節點1 -> 節點2）的時候剛剛被賦值為 -1。

這樣就造成了一個情況，即：計算minDist數組的時候，基于了本次松弛的 minDist數值，而不是上一次 松弛時候minDist的數值。
所以在每次計算 minDist 時候，要基于 對所有邊上一次松弛的 minDist 數值才行，所以我們要記錄上一次松弛的minDist。

代碼修改如下： （關鍵地方已經注釋）

// 版本二
#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;int main() {
int src, dst,k ,p1, p2, val ,m , n;cin >> n >> m;vector<vector<int>> grid;for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid.push_back({p1, p2, val});
}cin >> src >> dst >> k;vector<int> minDist(n + 1 , INT_MAX);
minDist[src] = 0;
vector<int> minDist_copy(n + 1); // 用來記錄上一次遍歷的結果
for (int i = 1; i <= k + 1; i++) {
minDist_copy = minDist; // 獲取上一次計算的結果
for (vector<int> &side : grid) {
int from = side[0];
int to = side[1];
int price = side[2];
// 注意使用 minDist_copy 來計算 minDist 
if (minDist_copy[from] != INT_MAX && minDist[to] > minDist_copy[from] + price) {  
minDist[to] = minDist_copy[from] + price;
}
}
}
if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到達終點
else cout << minDist[dst] << endl; // 到達終點最短路徑}

• 時間復雜度： O(K * E) , K為至多經過K個節點，E為圖中邊的數量
• 空間復雜度： O(N) ，即 minDist 數組所開辟的空間

其實邊的順序會影響我們每一次拓展的結果。

我來給大家舉個例子。

我上面講解中，給出的示例是這樣的：

4 4
1 2 -1
2 3 1
3 1 -1
3 4 1
1 4 3

我將示例中邊的順序改一下，給成：

4 4
3 1 -1
3 4 1
2 3 1
1 2 -1
1 4 3

所構成是圖是一樣的，都是如下的這個圖，但給出的邊的順序是不一樣的。

??

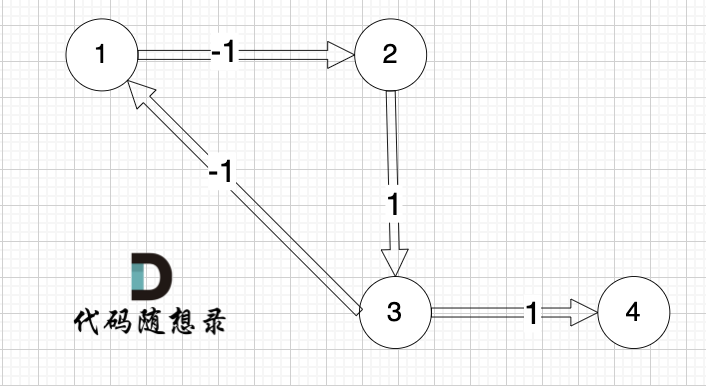再用版本一的代碼是運行一下，發現結果輸出是 1， 是對的。

??

分明剛剛輸出的結果是 -2，是錯誤的，怎么 一樣的圖，這次輸出的結果就對了呢？

其實這是和示例中給出的邊的順序是有關的，

我們按照修改后的示例再來模擬 對所有邊的第一次拓展情況。

初始化：

??

邊：節點3 -> 節點1，權值為-1 ，節點3還沒有被計算過，節點1 不更新。

邊：節點3 -> 節點4，權值為1 ，節點3還沒有被計算過，節點4 不更新。

邊：節點2 -> 節點3，權值為 1 ，節點2還沒有被計算過，節點3 不更新。

邊：節點1 -> 節點2，權值為 -1 ，minDist[2] > minDist[1] + (-1)，更新 minDist[2] = 0 + (-1) = -1 ，如圖：

??

以上是對所有邊 松弛一次的狀態。

可以發現 同樣的圖，邊的順序不一樣，使用版本一的代碼 每次松弛更新的節點也是不一樣的。

而邊的順序是隨機的，是題目給我們的，所以本題我們才需要 記錄上一次松弛的minDist，來保障 每一次對所有邊松弛的結果。

那么前面講解過的 94.城市間貨物運輸I 和 95.城市間貨物運輸II 也是bellman_ford經典算法，也沒使用 minDist_copy，怎么就沒問題呢？

如果沒看過我上面這兩篇講解的話，建議詳細學習上面兩篇，再看我下面講的區別，否則容易看不懂。

94.城市間貨物運輸I， 是沒有 負權回路的，那么 多松弛多少次，對結果都沒有影響。

求 節點1 到 節點n 的最短路徑，松弛n-1 次就夠了，松弛 大于 n-1次，結果也不會變。

那么在對所有邊進行第一次松弛的時候，如果基于 本次計算的 minDist 來計算 minDist （相當于多做松弛了），也是對最終結果沒影響。

95.城市間貨物運輸II 是判斷是否有 負權回路，一旦有負權回路， 對所有邊松弛 n-1 次以后，在做松弛 minDist 數值一定會變，根據這一點來判斷是否有負權回路。

所以，95.城市間貨物運輸II 只需要判斷minDist數值變化了就行，而 minDist 的數值對不對，并不是我們關心的。

那么本題 為什么計算minDist 一定要基于上次 的 minDist 數值。

其關鍵在于本題的兩個因素：

• 本題可以有負權回路，說明只要多做松弛，結果是會變的。
• 本題要求最多經過k個節點，對松弛次數是有限制的。

如果本題中 沒有負權回路的測試用例， 那版本一的代碼就可以過了，也就不用我費這么大口舌去講解的這個坑了。

本題也可以用 SPFA來做，關于 SPFA ，已經在這里 0094.城市間貨物運輸I-SPFA 有詳細講解。

使用SPFA算法解決本題的時候，關鍵在于 如何控制松弛k次。

其實實現不難，但有點技巧，可以用一個變量 que_size 記錄每一輪松弛入隊列的所有節點數量。

下一輪松弛的時候，就把隊列里 que_size 個節點都彈出來，就是上一輪松弛入隊列的節點。

代碼如下（詳細注釋）

#include <iostream>
#include <vector>
#include <queue>
#include <list>
#include <climits>
using namespace std;struct Edge { //鄰接表
int to;  // 鏈接的節點
int val; // 邊的權重Edge(int t, int w): to(t), val(w) {}  // 構造函數
};int main() {
int n, m, p1, p2, val;
cin >> n >> m;vector<list<Edge>> grid(n + 1); // 鄰接表// 將所有邊保存起來
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，權值為 val
grid[p1].push_back(Edge(p2, val));
}
int start, end, k;
cin >> start >> end >> k;k++;vector<int> minDist(n + 1 , INT_MAX);
vector<int> minDist_copy(n + 1); // 用來記錄每一次遍歷的結果minDist[start] = 0;queue<int> que;
que.push(start); // 隊列里放入起點int que_size;
while (k-- && !que.empty()) {minDist_copy = minDist; // 獲取上一次計算的結果
que_size = que.size(); // 記錄上次入隊列的節點個數
while (que_size--) { // 上一輪松弛入隊列的節點，這次對應的邊都要做松弛
int node = que.front(); que.pop();
for (Edge edge : grid[node]) {
int from = node;
int to = edge.to;
int price = edge.val;
if (minDist[to] > minDist_copy[from] + price) {
minDist[to] = minDist_copy[from] + price;
que.push(to);
}
}}
}
if (minDist[end] == INT_MAX) cout << "unreachable" << endl;
else cout << minDist[end] << endl;}

時間復雜度： O(K * H) H 為不確定數，取決于 圖的稠密度，但H 一定是小于等于 E 的

關于 SPFA的是時間復雜度分析，我在0094.城市間貨物運輸I-SPFA 有詳細講解

但大家會發現，以上代碼大家提交后，怎么耗時這么多？

??

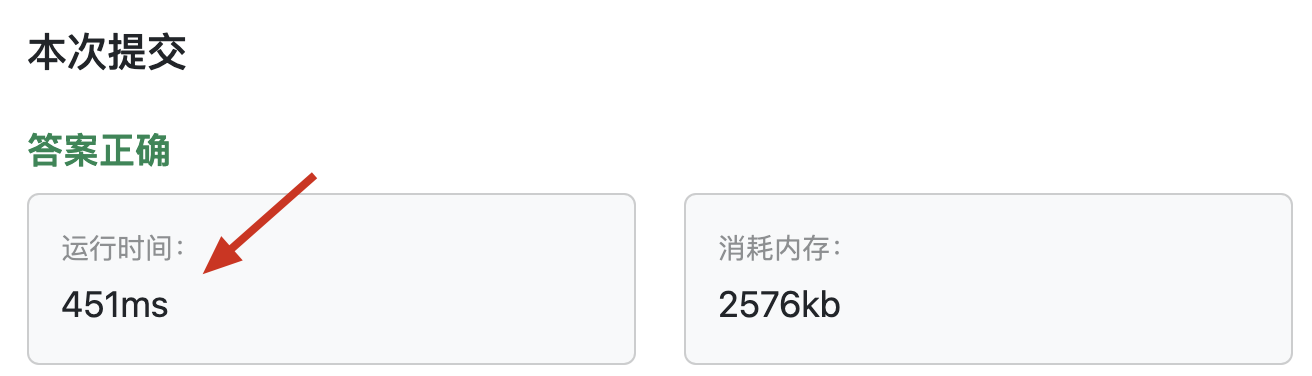理論上，SPFA的時間復雜度不是要比 bellman_ford 更優嗎？

怎么耗時多了這么多呢？

以上代碼有一個可以改進的點，每一輪松弛中，重復節點可以不用入隊列。

因為重復節點入隊列，下次從隊列里取節點的時候，該節點要取很多次，而且都是重復計算。

所以代碼可以優化成這樣：

#include <iostream>
#include <vector>
#include <queue>
#include <list>
#include <climits>
using namespace std;struct Edge { //鄰接表
int to;  // 鏈接的節點
int val; // 邊的權重Edge(int t, int w): to(t), val(w) {}  // 構造函數
};int main() {
int n, m, p1, p2, val;
cin >> n >> m;vector<list<Edge>> grid(n + 1); // 鄰接表// 將所有邊保存起來
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，權值為 val
grid[p1].push_back(Edge(p2, val));
}
int start, end, k;
cin >> start >> end >> k;k++;vector<int> minDist(n + 1 , INT_MAX);
vector<int> minDist_copy(n + 1); // 用來記錄每一次遍歷的結果minDist[start] = 0;queue<int> que;
que.push(start); // 隊列里放入起點int que_size;
while (k-- && !que.empty()) {vector<bool> visited(n + 1, false); // 每一輪松弛中，控制節點不用重復入隊列
minDist_copy = minDist; 
que_size = que.size(); 
while (que_size--) { 
int node = que.front(); que.pop();
for (Edge edge : grid[node]) {
int from = node;
int to = edge.to;
int price = edge.val;
if (minDist[to] > minDist_copy[from] + price) {
minDist[to] = minDist_copy[from] + price;
if(visited[to]) continue; // 不用重復放入隊列，但需要重復松弛，所以放在這里位置
visited[to] = true;
que.push(to);
}
}}
}
if (minDist[end] == INT_MAX) cout << "unreachable" << endl;
else cout << minDist[end] << endl;
}

以上代碼提交后，耗時情況：

??

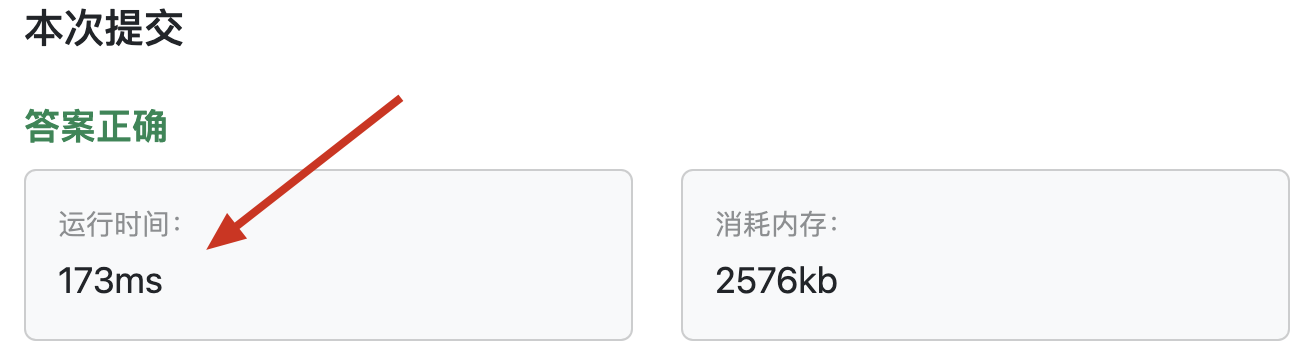大家發現 依然遠比 bellman_ford 的代碼版本 耗時高。

這又是為什么呢？

對于后臺數據，我特別制作的一個稠密大圖，該圖有250個節點和10000條邊， 在這種情況下， SPFA 的時間復雜度 是接近與 bellman_ford的。

但因為 SPFA 節點的進出隊列操作，耗時很大，所以相同的時間復雜度的情況下，SPFA 實際上更耗時了。

這一點我在 0094.城市間貨物運輸I-SPFA 有分析，感興趣的錄友再回頭去看看。

本題能否使用 dijkstra 算法呢？

dijkstra 是貪心的思路 每一次搜索都只會找距離源點最近的非訪問過的節點。

如果限制最多訪問k個節點，那么 dijkstra 未必能在有限次就能到達終點，即使在經過k個節點確實可以到達終點的情況下。

這么說大家會感覺有點抽象，我用 dijkstra樸素版精講 里的示例在舉例說明： （如果沒看過我講的dijkstra樸素版精講，建議去仔細看一下，否則下面講解容易看不懂）

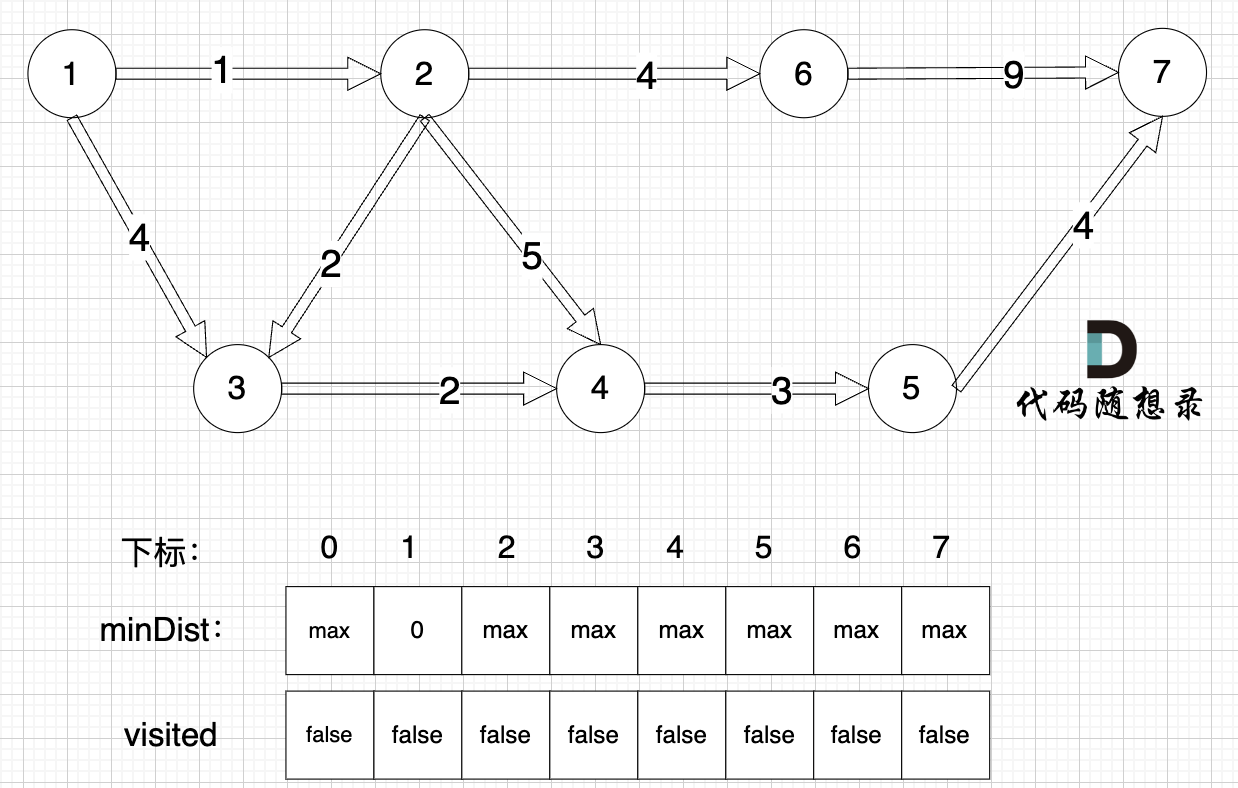
在以下這個圖中，求節點1 到 節點7 最多經過2個節點 的最短路是多少呢？

??

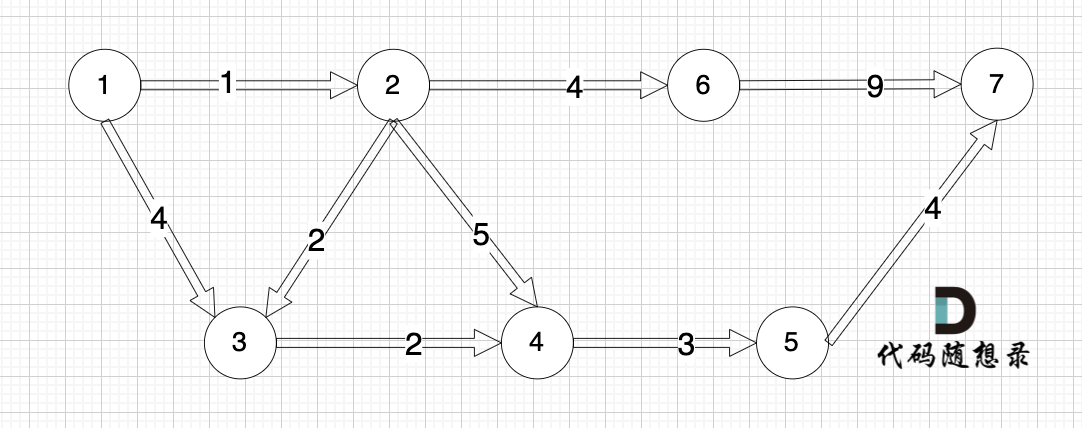最短路顯然是：

??

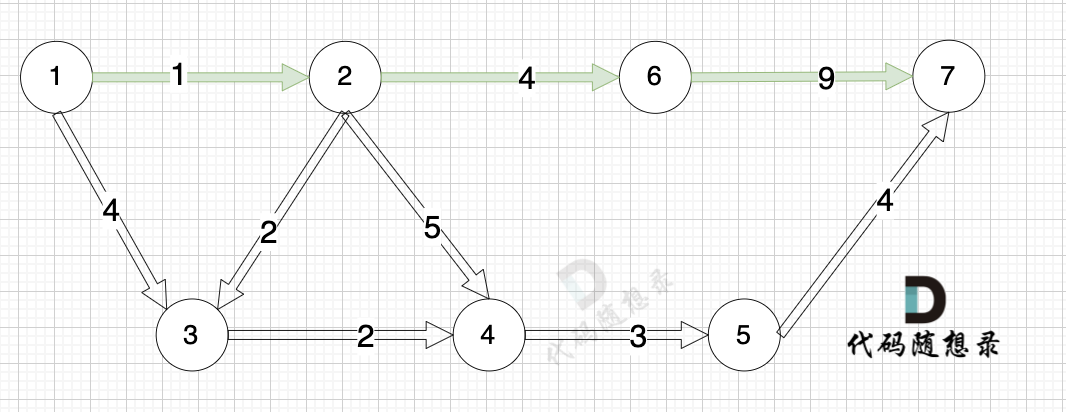最多經過2個節點，也就是3條邊相連的路線：節點1 -> 節點2 -> 節點6-> 節點7

如果是 dijkstra 求解的話，求解過程是這樣的： （下面是dijkstra的模擬過程，我精簡了很多，如果看不懂，一定要先看dijkstra樸素版精講）

初始化如圖所示：

??

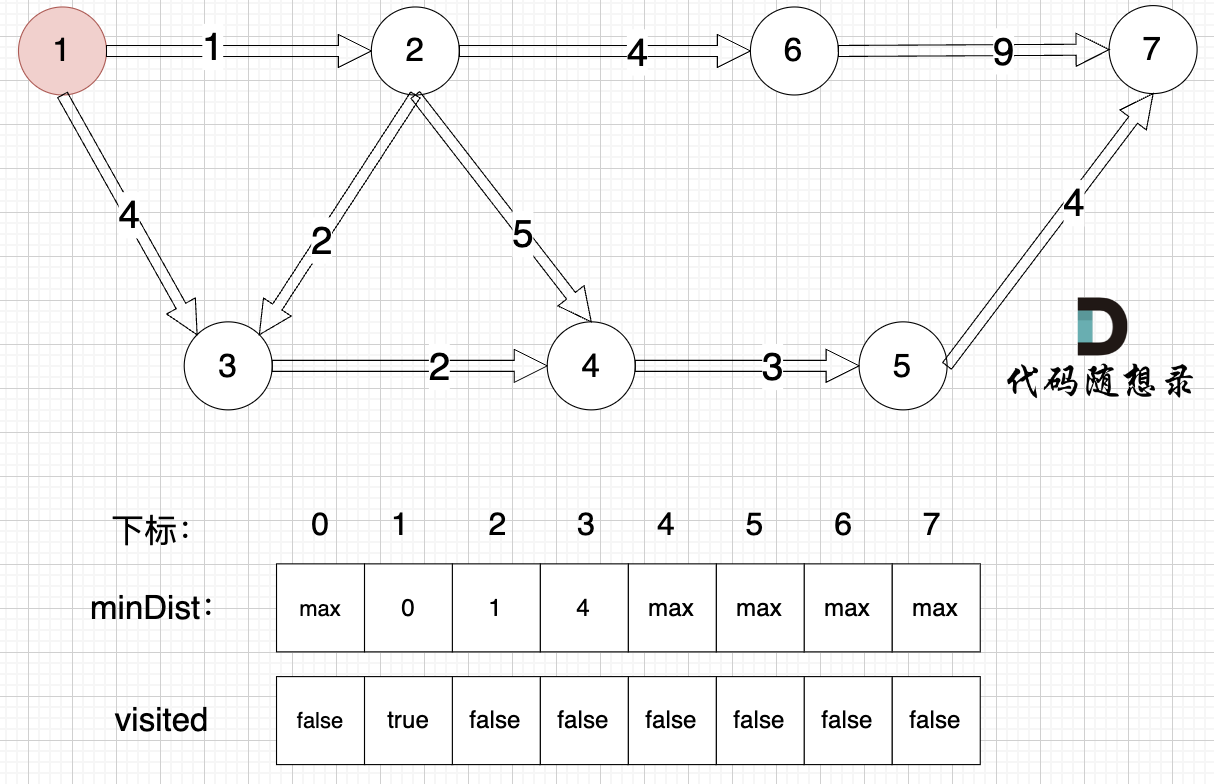
找距離源點最近且沒有被訪問過的節點，先找節點1

??

距離源點最近且沒有被訪問過的節點，找節點2：

??

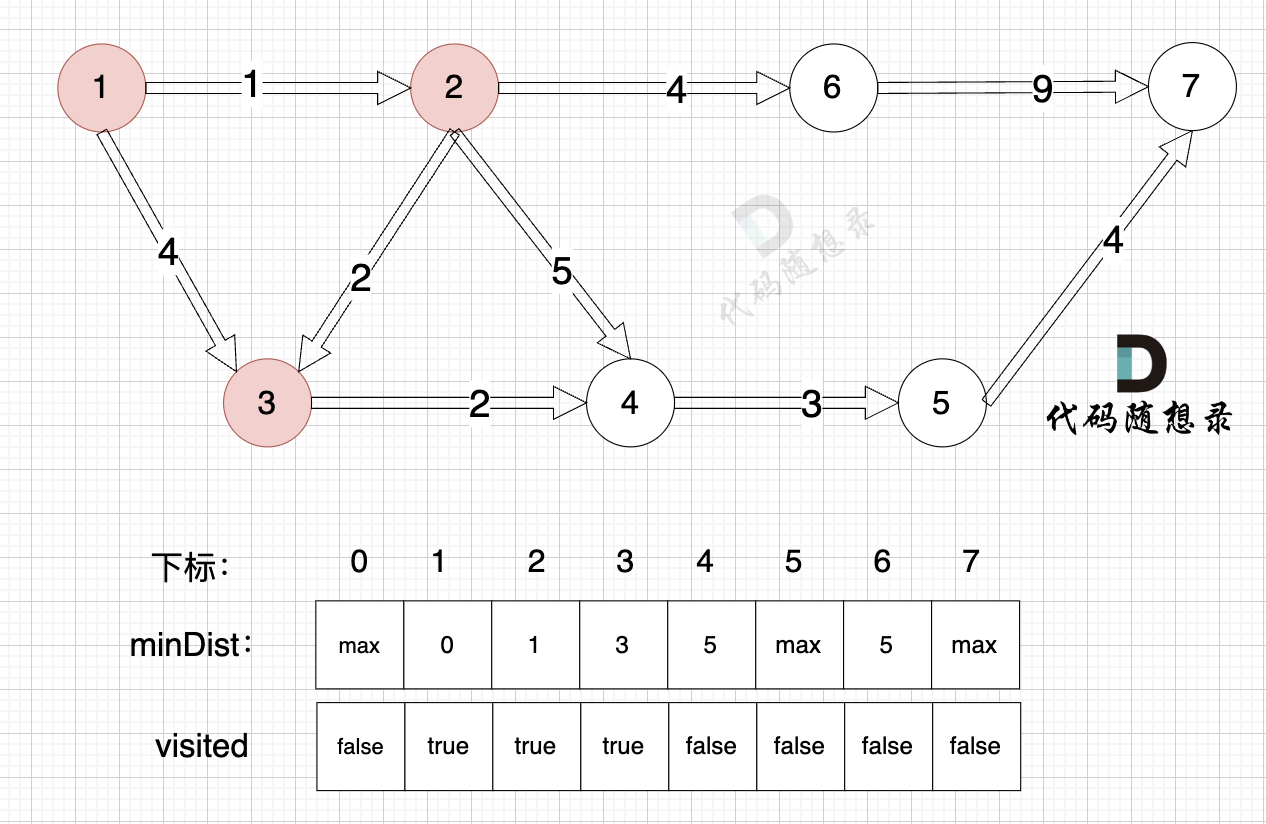
距離源點最近且沒有被訪問過的節點，找到節點3：

??

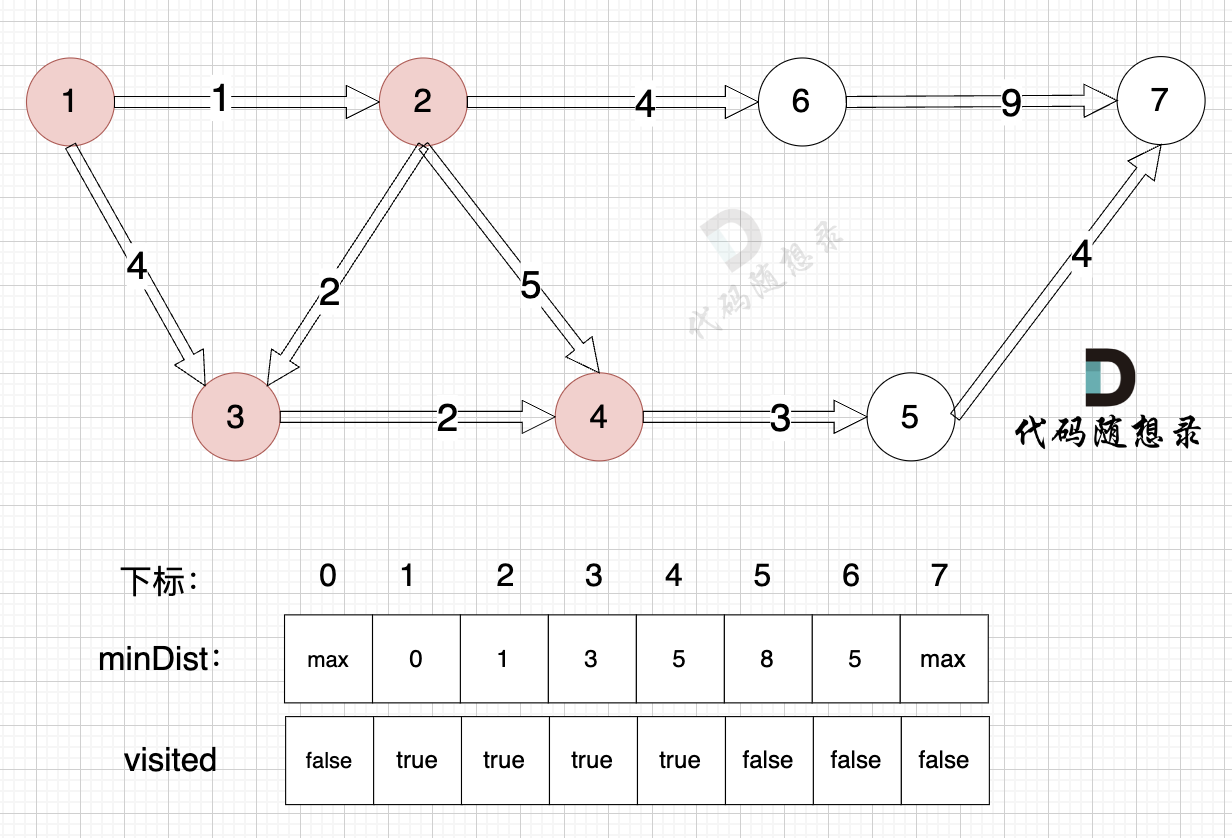
距離源點最近且沒有被訪問過的節點，找到節點4：

??

此時最多經過2個節點的搜索就完畢了，但結果中minDist[7] （即節點7的結果）并沒有被更。

那么 dijkstra 會告訴我們 節點1 到 節點7 最多經過2個節點的情況下是不可到達的。

通過以上模擬過程，大家應該能感受到 dijkstra 貪心的過程，正是因為 貪心，所以 dijkstra 找不到 節點1 -> 節點2 -> 節點6-> 節點7 這條路徑。

本題是單源有限最短路問題，也是 bellman_ford的一個拓展問題，如果理解bellman_ford 其實思路比較容易理解，但有很多細節。

例如 為什么要用 minDist_copy 來記錄上一輪 松弛的結果。 這也是本篇我為什么花了這么大篇幅講解的關鍵所在。

接下來，還給大家做了四個拓展：

• 邊的順序的影響
• 本題的本質
• SPFA的解法
• 能否用dijkstra

學透了以上四個拓展，相信大家會對bellman_ford有更深入的理解。

本題是經典的多源最短路問題。

在這之前我們講解過，dijkstra樸素版、dijkstra堆優化、Bellman算法、Bellman隊列優化（SPFA） 都是單源最短路，即只能有一個起點。

而本題是多源最短路，即 求多個起點到多個終點的多條最短路徑。

通過本題，我們來系統講解一個新的最短路算法-Floyd 算法。

Floyd 算法對邊的權值正負沒有要求，都可以處理。

Floyd算法核心思想是動態規劃。

例如我們再求節點1 到 節點9 的最短距離，用二維數組來表示即：grid[1][9]，如果最短距離是10 ，那就是 grid[1][9] = 10。

那 節點1 到 節點9 的最短距離 是不是可以由 節點1 到節點5的最短距離 + 節點5到節點9的最短距離組成呢？

即 grid[1][9] = grid[1][5] + grid[5][9]

節點1 到節點5的最短距離 是不是可以有 節點1 到 節點3的最短距離 + 節點3 到 節點5 的最短距離組成呢？

即 grid[1][5] = grid[1][3] + grid[3][5]

以此類推，節點1 到 節點3的最短距離 可以由更小的區間組成。

那么這樣我們是不是就找到了，子問題推導求出整體最優方案的遞歸關系呢。

節點1 到 節點9 的最短距離 可以由 節點1 到節點5的最短距離 + 節點5到節點9的最短距離組成， 也可以有 節點1 到節點7的最短距離 + 節點7 到節點9的最短距離的距離組成。

那么選哪個呢？

是不是 要選一個最小的，畢竟是求最短路。

此時我們已經接近明確遞歸公式了。

之前在講解動態規劃的時候，給出過動規五部曲：

• 確定dp數組（dp table）以及下標的含義
• 確定遞推公式
• dp數組如何初始化
• 確定遍歷順序
• 舉例推導dp數組

那么接下來我們還是用這五部來給大家講解 Floyd。

1、確定dp數組（dp table）以及下標的含義

這里我們用 grid數組來存圖，那就把dp數組命名為 grid。

grid[i][j][k] = m，表示 節點i 到 節點j 以[1…k] 集合為中間節點的最短距離為m。

可能有錄友會想，憑什么就這么定義呢？

節點i 到 節點j 的最短距離為m，這句話可以理解，但 以[1…k]集合為中間節點就理解不遼了。

節點i 到 節點j 的最短路徑中 一定是經過很多節點，那么這個集合用[1…k] 來表示。

你可以反過來想，節點i 到 節點j 中間一定經過很多節點，那么你能用什么方式來表述中間這么多節點呢？

所以 這里的k不能單獨指某個節點，k 一定要表示一個集合，即[1…k] ，表示節點1 到 節點k 一共k個節點的集合。

2、確定遞推公式

在上面的分析中我們已經初步感受到了遞推的關系。

我們分兩種情況：

1. 節點i 到 節點j 的最短路徑經過節點k
2. 節點i 到 節點j 的最短路徑不經過節點k

對于第一種情況，grid[i][j][k] = grid[i][k][k - 1] + grid[k][j][k - 1]?

節點i 到 節點k 的最短距離 是不經過節點k，中間節點集合為[1…k-1]，所以 表示為grid[i][k][k - 1]?

節點k 到 節點j 的最短距離 也是不經過節點k，中間節點集合為[1…k-1]，所以表示為 grid[k][j][k - 1]?

第二種情況，grid[i][j][k] = grid[i][j][k - 1]?

如果節點i 到 節點j的最短距離 不經過節點k，那么 中間節點集合[1…k-1]，表示為 grid[i][j][k - 1]?

因為我們是求最短路，對于這兩種情況自然是取最小值。

即： grid[i][j][k] = min(grid[i][k][k - 1] + grid[k][j][k - 1]， grid[i][j][k - 1])?

3、dp數組如何初始化

grid[i][j][k] = m，表示 節點i 到 節點j 以[1…k] 集合為中間節點的最短距離為m。

剛開始初始化k 是不確定的。

例如題目中只是輸入邊（節點2 -> 節點6，權值為3），那么grid[2][6][k] = 3，k需要填什么呢？

把k 填成1，那如何上來就知道 節點2 經過節點1 到達節點6的最短距離是多少 呢。

所以 只能 把k 賦值為 0，本題 節點0 是無意義的，節點是從1 到 n。

這樣我們在下一輪計算的時候，就可以根據 grid[i][j][0] 來計算 grid[i][j][1]，此時的 grid[i][j][1] 就是 節點i 經過節點1 到達 節點j 的最小距離了。

grid數組是一個三維數組，那么我們初始化的數據在 i 與 j 構成的平層，如圖：

??

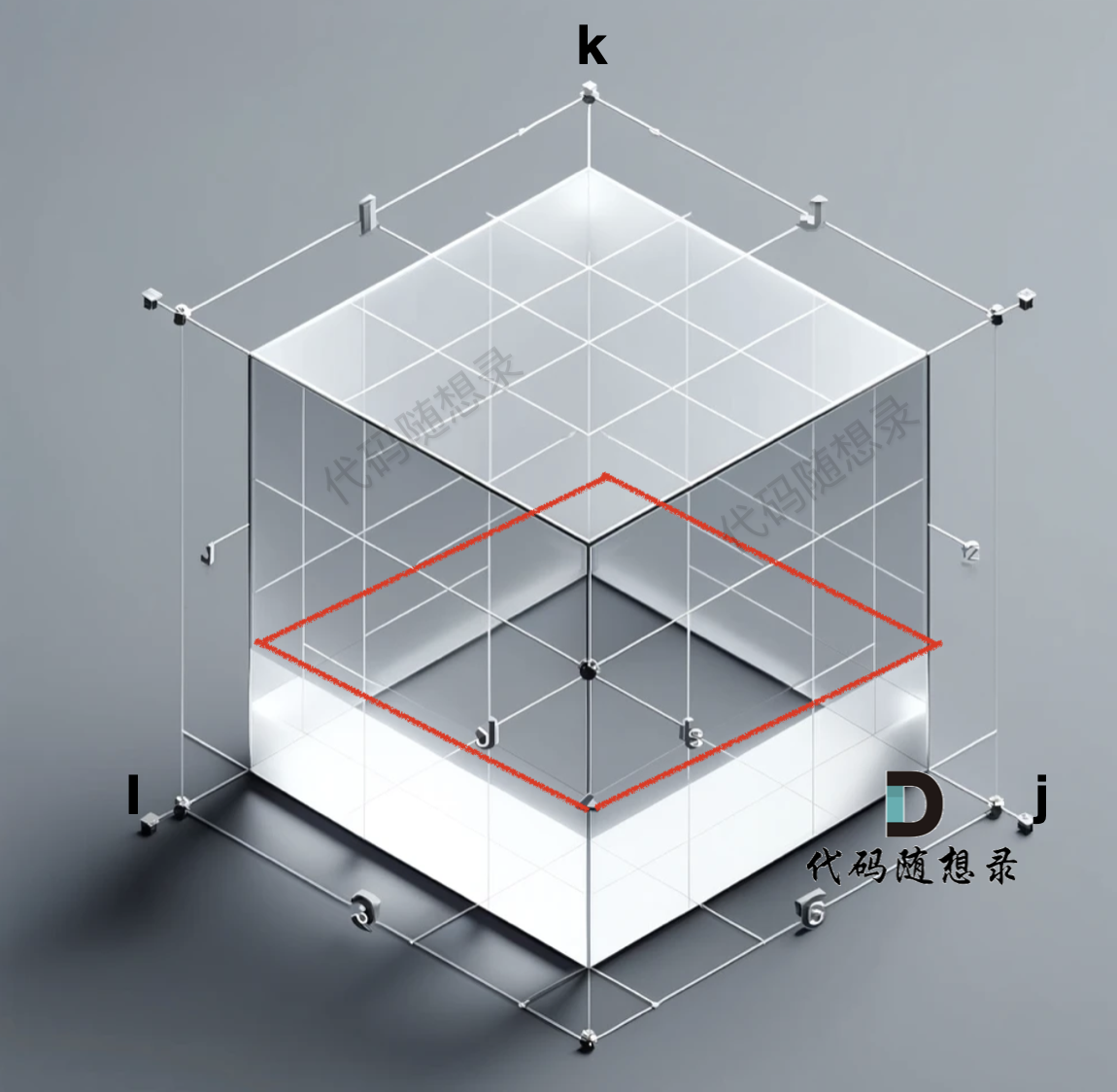紅色的 底部一層是我們初始化好的數據，注意：從三維角度去看初始化的數據很重要，下面我們在聊遍歷順序的時候還會再講。

所以初始化代碼：

vector<vector<vector<int>>> grid(n + 1, vector<vector<int>>(n + 1, vector<int>(n + 1, 10005)));  // C++定義了一個三位數組，10005是因為邊的最大距離是10^4for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid[p1][p2][0] = val;
grid[p2][p1][0] = val; // 注意這里是雙向圖
} 

grid數組中其他元素數值應該初始化多少呢？

本題求的是最小值，所以輸入數據沒有涉及到的節點的情況都應該初始為一個最大數。

這樣才不會影響，每次計算去最小值的時候 初始值對計算結果的影響。

所以grid數組的定義可以是：

// C++寫法，定義了一個三位數組，10005是因為邊的最大距離是10^4
vector<vector<vector<int>>> grid(n + 1, vector<vector<int>>(n + 1, vector<int>(n + 1, 10005)));  

4、確定遍歷順序

從遞推公式：grid[i][j][k] = min(grid[i][k][k - 1] + grid[k][j][k - 1]， grid[i][j][k - 1])? 可以看出，我們需要三個for循環，分別遍歷i，j 和k

而 k 依賴于 k - 1， i 和j 的到 并不依賴與 i - 1 或者 j - 1 等等。

那么這三個for的嵌套順序應該是什么樣的呢？

我們來看初始化，我們是把 k =0 的 i 和j 對應的數值都初始化了，這樣才能去計算 k = 1 的時候 i 和 j 對應的數值。

這就好比是一個三維坐標，i 和j 是平層，而k 是 垂直向上 的。

遍歷的順序是從底向上 一層一層去遍歷。

所以遍歷k 的for循環一定是在最外面，這樣才能一層一層去遍歷。如圖：

??

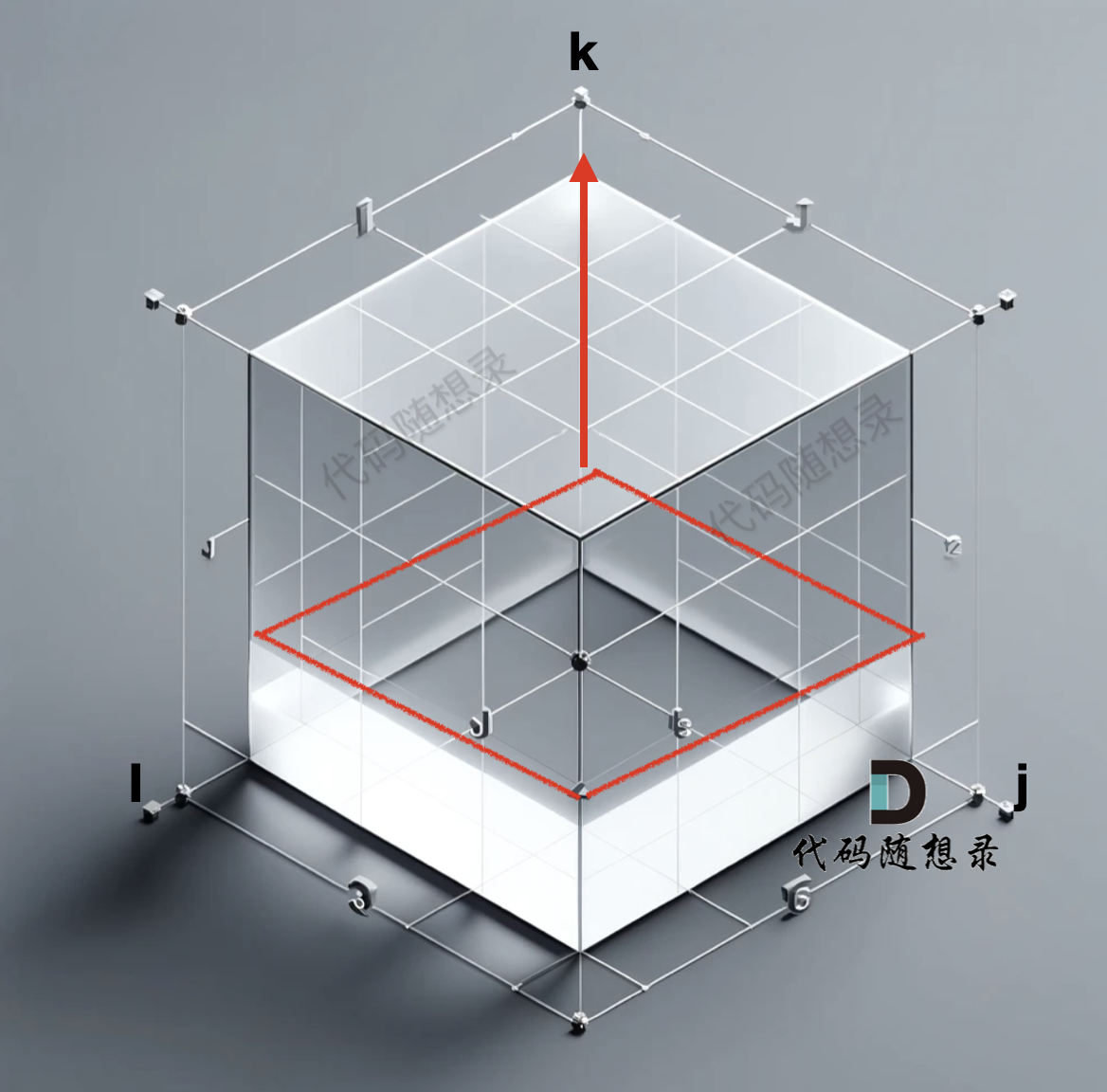至于遍歷 i 和 j 的話，for 循環的先后順序無所謂。

代碼如下：

for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
grid[i][j][k] = min(grid[i][j][k-1], grid[i][k][k-1] + grid[k][j][k-1]);
}
}
}

有錄友可能想，難道 遍歷k 放在最里層就不行嗎？

k 放在最里層，代碼是這樣：

for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
grid[i][j][k] = min(grid[i][j][k-1], grid[i][k][k-1] + grid[k][j][k-1]);
}
}
}

此時就遍歷了 j 與 k 形成一個平面，i 則是縱面，那遍歷 就是這樣的：

??

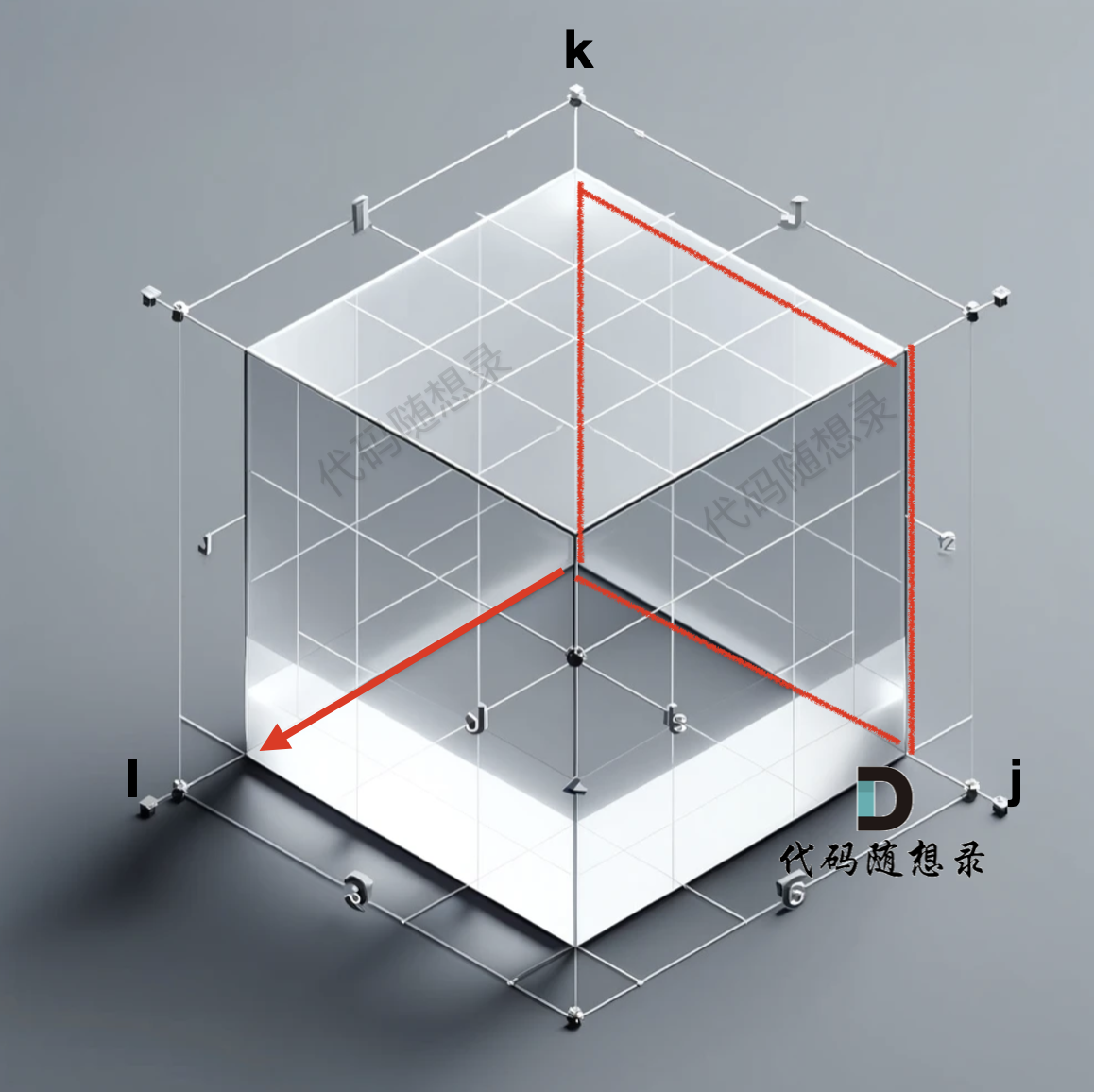而我們初始化的數據 是 k 為0， i 和 j 形成的平面做初始化，如果以 k 和 j 形成的平面去一層一層遍歷，就造成了 遞推公式 用不上上一輪計算的結果，從而導致結果不對（初始化的部分是 i 與j 形成的平面，在初始部分有講過）。

我再給大家舉一個測試用例

5 4
1 2 10
1 3 1
3 4 1
4 2 1
1
1 2

就是圖：

??

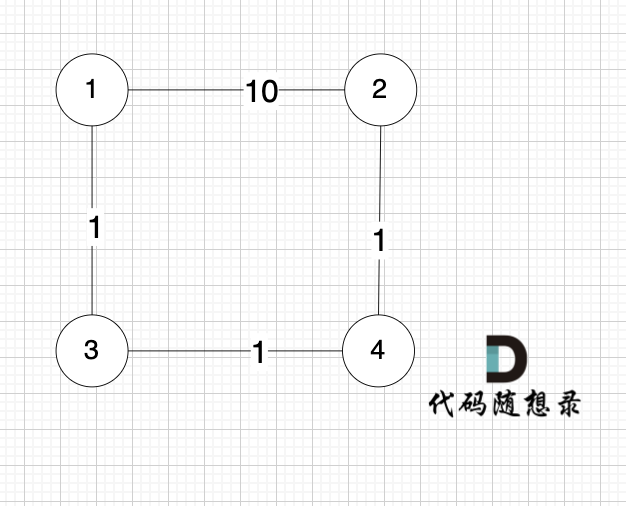求節點1 到 節點 2 的最短距離，運行結果是 10 ，但正確的結果很明顯是3。

為什么呢？

因為 k 放在最里面，先就把 節點1 和 節點 2 的最短距離就確定了，后面再也不會計算節點 1 和 節點 2的距離，同時也不會基于 初始化或者之前計算過的結果來計算，即：不會考慮 節點1 到 節點3， 節點3 到節點 4，節點4到節點2 的距離。

造成這一原因，是 在三維立體坐標中， 我們初始化的是 i 和 i 在k 為0 所構成的平面，但遍歷的時候 是以 j 和 k構成的平面以 i 為垂直方向去層次遍歷。

而遍歷k 的for循環如果放在中間呢，同樣是 j 與k 行程一個平面，i 是縱面，遍歷的也是這樣：

??

同樣不能完全用上初始化 和 上一層計算的結果。

根據這個情況再舉一個例子：

5 2
1 2 1
2 3 10
1
1 3

圖：

??

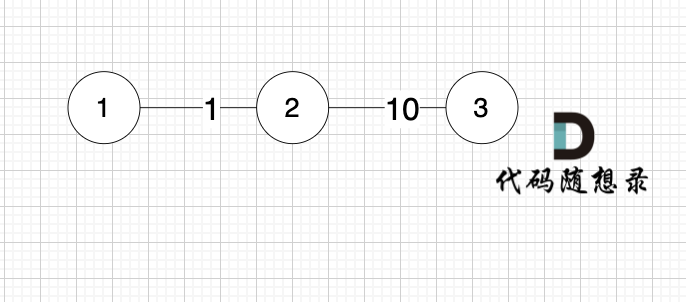求 節點1 到節點3 的最短距離，如果k循環放中間，程序的運行結果是 -1，也就是不能到達節點3。

在計算 grid[i][j][k] 的時候，需要基于 grid[i][k][k-1] 和 grid[k][j][k-1]的數值。

也就是 計算 grid[1][3][2] （表示節點1 到 節點3，經過節點2） 的時候，需要基于 grid[1][2][1] 和 grid[2][3][1]的數值，而 我們初始化，只初始化了 k為0 的那一層。

造成這一原因 依然是 在三維立體坐標中， 我們初始化的是 i 和 j 在k 為0 所構成的平面，但遍歷的時候 是以 j 和 k構成的平面以 i 為垂直方向去層次遍歷。

很多錄友對于 floyd算法的遍歷順序搞不懂，其實 是沒有從三維的角度去思考，同時我把三維立體圖給大家畫出來，遍歷順序標出來，大家就很容易想明白，為什么 k 放在最外層 才能用上 初始化和上一輪計算的結果了。

5、舉例推導dp數組

這里涉及到 三維矩陣，可以一層一層打印出來去分析，例如k=0 的這一層，k = 1的這一層，但一起把三維帶數據的圖畫出來其實不太好畫。

以上分析完畢，最后代碼如下：

#include <iostream>
#include <vector>
#include <list>
using namespace std;int main() {
int n, m, p1, p2, val;
cin >> n >> m;vector<vector<vector<int>>> grid(n + 1, vector<vector<int>>(n + 1, vector<int>(n + 1, 10005)));  // 因為邊的最大距離是10^4
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid[p1][p2][0] = val;
grid[p2][p1][0] = val; // 注意這里是雙向圖}
// 開始 floyd
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
grid[i][j][k] = min(grid[i][j][k-1], grid[i][k][k-1] + grid[k][j][k-1]);
}
}
}
// 輸出結果
int z, start, end;
cin >> z;
while (z--) {
cin >> start >> end;
if (grid[start][end][n] == 10005) cout << -1 << endl;
else cout << grid[start][end][n] << endl;
}
}

這里 我們可以做一下 空間上的優化，從滾動數組的角度來看，我們定義一個 grid[n + 1][ n + 1][2] 這么大的數組就可以，因為k 只是依賴于 k-1的狀態，并不需要記錄k-2，k-3，k-4 等等這些狀態。

那么我們只需要記錄 grid[i][j][1] 和 grid[i][j][0] 就好，之后就是 grid[i][j][1] 和 grid[i][j][0] 交替滾動。

在進一步想，如果本層計算（本層計算即k相同，從三維角度來講） gird[i][j] 用到了 本層中剛計算好的 grid[i][k] 會有什么問題嗎？

如果 本層剛計算好的 grid[i][k] 比上一層 （即k-1層）計算的 grid[i][k] 小，說明確實有 i 到 k 的更短路徑，那么基于 更小的 grid[i][k] 去計算 gird[i][j] 沒有問題。

如果 本層剛計算好的 grid[i][k] 比上一層 （即k-1層）計算的 grid[i][k] 大， 這不可能，因為這樣也不會做更新 grid[i][k]的操作。

所以本層計算中，使用了本層計算過的 grid[i][k] 和 grid[k][j] 是沒問題的。

那么就沒必要區分，grid[i][k] 和 grid[k][j] 是 屬于 k - 1 層的呢，還是 k 層的。

所以遞歸公式可以為：

grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]);

基于二維數組的本題代碼為：

#include <iostream>
#include <vector>
using namespace std;int main() {
int n, m, p1, p2, val;
cin >> n >> m;vector<vector<int>> grid(n + 1, vector<int>(n + 1, 10005));  // 因為邊的最大距離是10^4for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid[p1][p2] = val;
grid[p2][p1] = val; // 注意這里是雙向圖}
// 開始 floyd
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]);
}
}
}
// 輸出結果
int z, start, end;
cin >> z;
while (z--) {
cin >> start >> end;
if (grid[start][end] == 10005) cout << -1 << endl;
else cout << grid[start][end] << endl;
}
}

• 時間復雜度： O(n^3)
• 空間復雜度：O(n^2)

本期如果上來只用二維數組來講的話，其實更容易，但遍歷順序那里用二維數組其實是講不清楚的，所以我直接用三維數組來講，目的是將遍歷順序這里講清楚。

理解了遍歷順序才是floyd算法最精髓的地方。

floyd算法的時間復雜度相對較高，適合 稠密圖且源點較多的情況。

如果是稀疏圖，floyd是從節點的角度去計算了，例如 圖中節點數量是 1000，就一條邊，那 floyd的時間復雜度依然是 O(n^3) 。

如果 源點少，其實可以 多次dijsktra 求源點到終點。