Python特征工程 — 1.4 特征歸一化方法詳解

1 Min-Max歸一化

方法1：自定義的Min-Max歸一化封裝函數

方法2：?scikit-learn庫中的MinMaxScaler

2 Z-score歸一化

方法1：自定義的Z-score歸一化封裝函數

方法2：?scikit-learn庫中的StandardScaler

3 最大值歸一化

4 L1歸一化

方法1：自定義的Z-score歸一化封裝函數

方法2：?scikit-learn庫中的Normalizer

5 L2歸一化

方法1：自定義的L2歸一化歸一化封裝函數

方法2：?scikit-learn庫中的Normalizer

6?Box-Cox歸一化

方法1：自定義的L2歸一化歸一化封裝函數

方法2：?scipy庫的boxcox

7 選擇哪種歸一化

實驗數據：鏈接：https://pan.baidu.com/s/1yT1ct_ZM5uFLgcYsaBxnHg?pwd=czum? 提取碼：czum?

實驗數據介紹：參考文章1.2節（數據介紹鏈接）

1 Min-Max歸一化

最小-最大歸一化（Min-Max Normalization）是一種將數據縮放到特定范圍內的線性變換方法，通常是[0, 1]。這種方法保證了數據的最小值被映射為0，最大值被映射為1，中間的值則按比例進行縮放。

最小-最大歸一化的公式為：

其中，是歸一化后的值，x 是原始數據點，max(x) 和 min(x) 分別是數據集中的最大值和最小值。

示例程序將使用兩種方法實現，自定義的最小-最大歸一化封裝函數，并使用scikit-learn庫中的MinMaxScaler類作為第二種方法來實現歸一化。以下是具體的實現：

方法1：自定義的Min-Max歸一化封裝函數

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 定義最小-最大歸一化函數，使其能夠處理DataFrame或Series
def min_max_normalization(data):# 檢查數據是否為pandas Series或DataFrameif isinstance(data, pd.Series):# 如果是Series，直接應用歸一化min_val = data.min()max_val = data.max()data_normalized = (data - min_val) / (max_val - min_val)return data_normalizedelif isinstance(data, pd.DataFrame):# 如果是DataFrame，逐列應用歸一化return (data - data.min()) / (data.max() - data.min())else:raise ValueError("Input data must be a pandas Series or DataFrame")# 方法一：使用自定義函數進行歸一化
data_normalized_custom = min_max_normalization(data['Total_Spending'])

方法2：?`scikit-learn`庫中的`MinMaxScaler`

from sklearn.preprocessing import MinMaxScaler# 方法二：使用 scikit-learn 的 MinMaxScaler 進行歸一化
scaler = MinMaxScaler()
data_normalized_sklearn = scaler.fit_transform(data[['Total_Spending']])

plt.figure(figsize=(14, 5))
# 繪制原始數據和歸一化數據的對比圖
plt.subplot(1, 2, 1)
# 繪制原始數據的線條圖
plt.plot(data['Total_Spending'], marker='o')
plt.title('Original Data')
plt.xlabel('Index')
plt.ylabel('Value')plt.subplot(1, 2, 2)
# 繪制自定義歸一化方法的數據的線條圖
plt.plot(data_normalized_custom, label='Normalized (Custom)', linestyle='--', marker='x')
# 繪制 scikit-learn 歸一化方法的數據的線條圖
plt.plot(data_normalized_sklearn, label='Normalized (scikit-learn)', linestyle='-.', marker='s')# 添加圖例、標題和坐標軸標簽
# plt.legend(loc='upper center')
plt.title('min_max_normalization')
plt.xlabel('Index')
plt.ylabel('Value')

運行結果如下：?

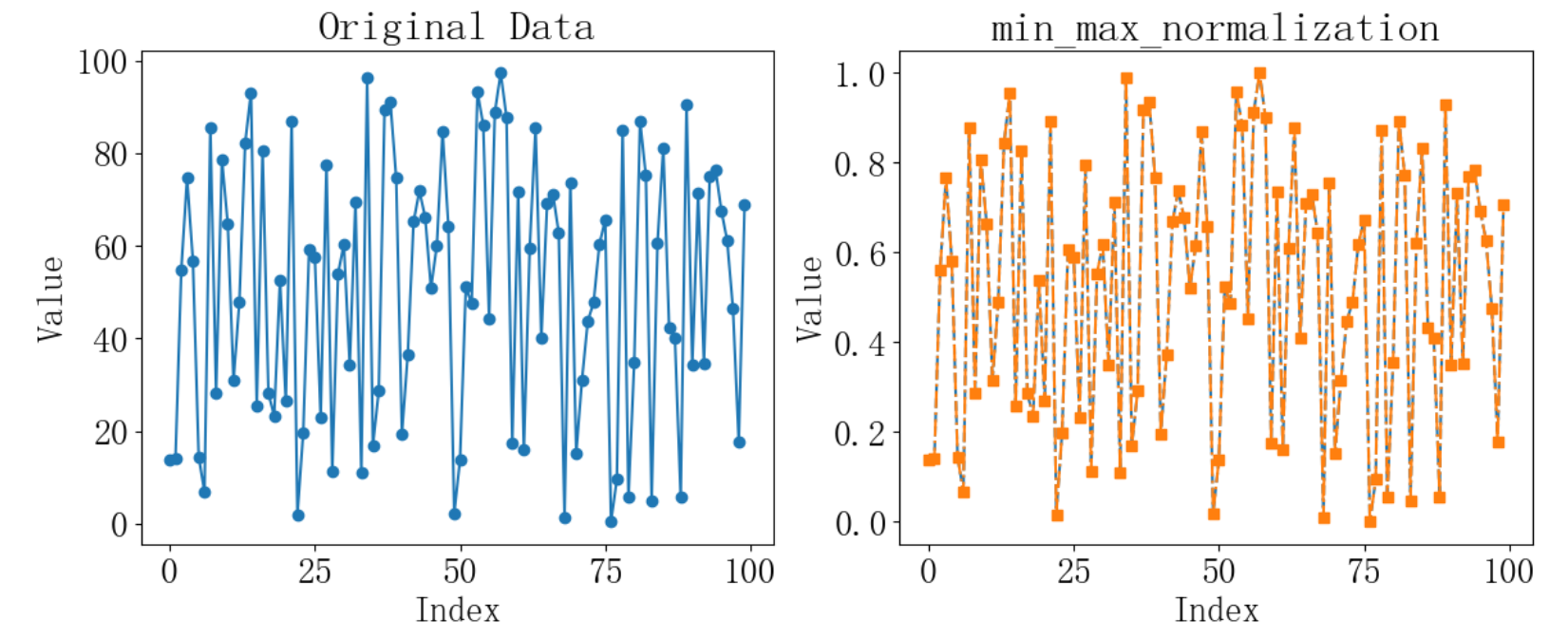
2 Z-score歸一化

?Z-score歸一化，也稱為標準化（Standardization），是一種將數據按比例縮放至特定均值（mean）和標準差（standard deviation）的方法。其目的是將數據轉換為一個標準分布，其中數據的均值為0，標準差為1。Z-score歸一化它確保了不同特征具有相同的尺度和分布特性。?

示例程序將使用兩種方法實現，自定義的最小-最大歸一化封裝函數，并使用scikit-learn庫中的StandardScaler類作為第二種方法來實現歸一化。以下是具體的實現：

方法1：自定義的Z-score歸一化封裝函數

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 使用自定義函數進行Z-score歸一化
def z_score_normalization(data):if isinstance(data, (pd.Series, pd.DataFrame)):mean = data.mean()std = data.std()data_normalized = (data - mean) / stdreturn data_normalizedelse:raise ValueError("Input data must be a pandas Series or DataFrame")# 使用自定義函數進行Z-score歸一化
data_normalized_custom = z_score_normalization(data.iloc[:, 7:10])

方法2：?`scikit-learn`庫中的`StandardScaler`

from sklearn.preprocessing import StandardScaler# 使用 scikit-learn 的 StandardScaler 進行Z-score歸一化
scaler = StandardScaler()
data_normalized_sklearn = scaler.fit_transform(data.iloc[:, 7:10])
data_normalized_sklearn = pd.DataFrame(data_normalized_sklearn, columns=data.columns[7:10])

?運行結果如下，選取的3個數據有不同的尺度，最后歸一化到了0-1的范圍：??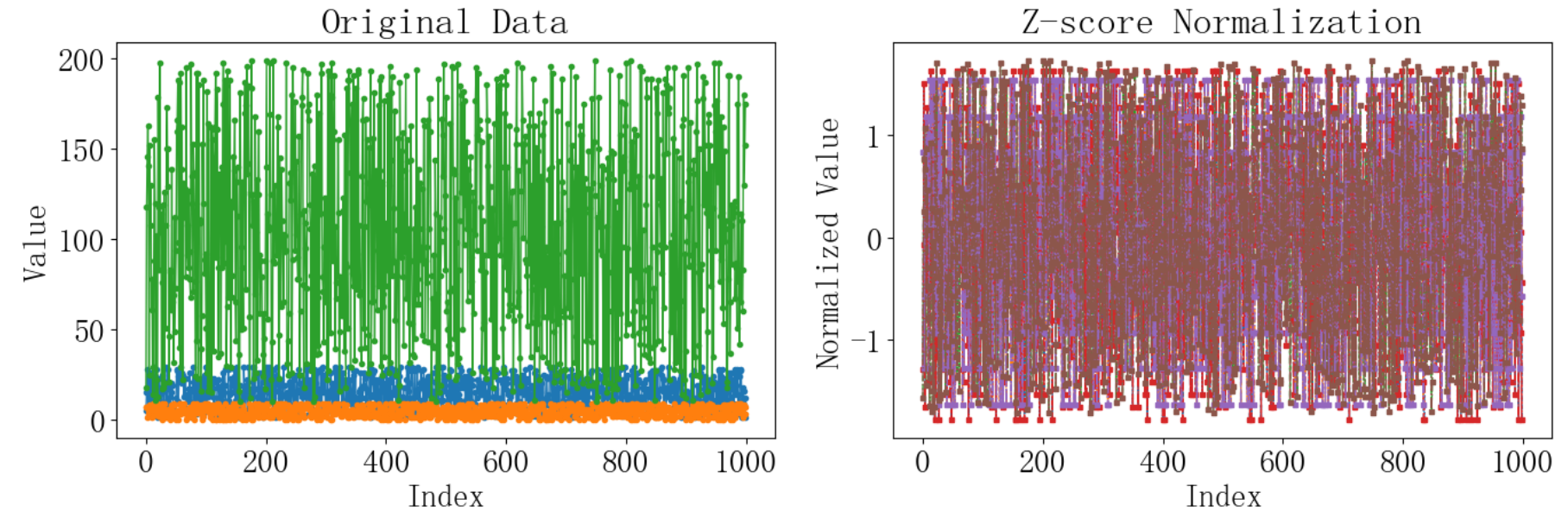

3 最大值歸一化

最大最小值歸一化（Min-Max Normalization）是一種線性變換，它將數據的最小值映射到0，最大值映射到1，所有其他值按比例映射到0和1之間。

最大最小值歸一化的公式為：

其中：x?是原始數據點，x′?是歸一化后的數據點，min(x)?是數據中的最小值，max(x)?是數據中的最大值。

示例程序自定義的最小-最大歸一化封裝函數，以下是具體的實現：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 使用自定義函數進行最大最小值歸一化
def min_max_normalization(data):if isinstance(data, (pd.Series, pd.DataFrame)):data_normalized = (data - data.min()) / (data.max() - data.min())return data_normalizedelse:raise ValueError("Input data must be a pandas Series or DataFrame")# 使用自定義函數進行最大最小值歸一化
data_normalized_custom = min_max_normalization(data.iloc[:, 7:10])# 繪制原始數據和歸一化數據的對比圖
plt.figure(figsize=(14, 5))plt.subplot(1, 2, 1)
# 繪制原始數據的線條圖，假設我們有3列數據
for idx, col in enumerate(data.columns[7:10]):plt.plot(data.index, data[col], marker='o', linewidth=1, markersize=3)plt.title('Original Data')
plt.xlabel('Index')
plt.ylabel('Value')plt.subplot(1, 2, 2)
# 繪制自定義最大最小值歸一化方法的數據的線條圖
for idx, col in enumerate(data.columns[7:10]):plt.plot(data.index, data_normalized_custom[col], linestyle='--', marker='x', linewidth=1, markersize=3)# 添加圖例、標題和坐標軸標簽
plt.title('Min-Max Normalization')
plt.xlabel('Index')
plt.ylabel('Normalized Value')# 顯示圖形
plt.tight_layout()
plt.show()

運行結果如下：

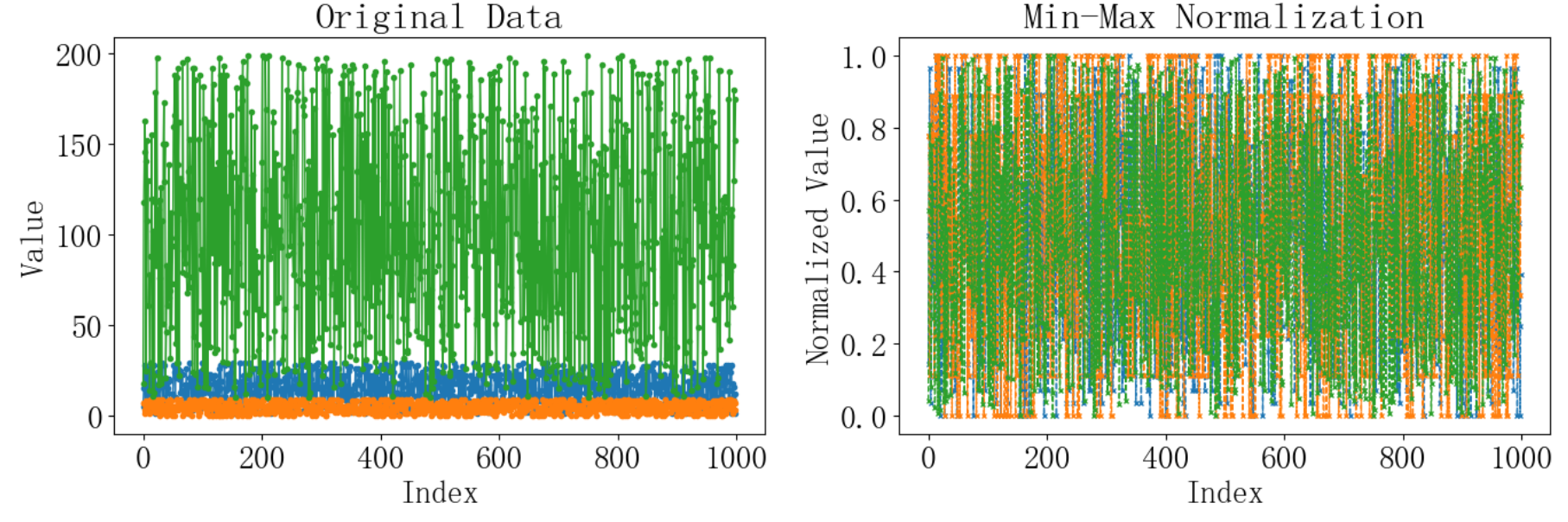
4 L1歸一化

L1歸一化，也稱為曼哈頓距離歸一化或1-范數歸一化，是一種將數據的特征向量按其絕對值的總和進行歸一化的方法。其目的是將每個特征的絕對值加和為1。L1歸一化在某些特定的機器學習算法中很有用，比如在L1正則化（Lasso回歸）中。

L1歸一化的公式為：

x?是原始數據向量。
x′?是歸一化后的數據向量。
∑∣x∣?是向量x中所有元素絕對值的總和。

L1歸一化的優點包括：

它對異常值具有一定的魯棒性，因為異常值不會像在L2歸一化中那樣對結果產生過大的影響。
它可以將數據轉換為稀疏表示，這在某些類型的機器學習算法中是有利的。

示例程序將使用兩種方法實現，自定義的L1歸一化封裝函數，并使用scikit-learn庫中的Normalizer類作為第二種方法來實現歸一化。以下是具體的實現：

方法1：自定義的Z-score歸一化封裝函數

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 使用自定義函數進行L1歸一化
def l1_normalization(data):if isinstance(data, pd.Series):data = data.to_frame()  # 將Series轉換為DataFrameif isinstance(data, pd.DataFrame):norms = np.abs(data).sum(axis=1)data_normalized = data.div(norms, axis=0)return data_normalizedelse:raise ValueError("Input data must be a pandas Series or DataFrame")# 使用自定義函數進行L1歸一化
data_normalized_custom = l1_normalization(data.iloc[:, 7:10])

方法2：?`scikit-learn`庫中的`Normalizer`

from sklearn.preprocessing import Normalizer# 使用 scikit-learn 的 Normalizer 進行L1歸一化
normalizer = Normalizer(norm='l1')
data_normalized_sklearn_l1 = normalizer.fit_transform(data.iloc[:, 7:10])
data_normalized_sklearn_l1 = pd.DataFrame(data_normalized_sklearn_l1, columns=data.columns[7:10])

# 繪制原始數據和歸一化數據的對比圖
plt.figure(figsize=(14, 5))
plt.subplot(1, 2, 1)
# 繪制原始數據的線條圖
for idx, col in enumerate(data.columns[7:10]):plt.plot(data.index, data[col], label=f'Original {col}', marker='o', linewidth=1, markersize=3)plt.title('Original Data')
plt.xlabel('Index')
plt.ylabel('Value')
plt.subplot(1, 2, 2)
# 繪制自定義L1歸一化方法的數據的線條圖
for idx, col in enumerate(data_normalized_custom.columns):plt.plot(data.index, data_normalized_custom[col], linestyle='--', marker='x', linewidth=1, markersize=3)
# 繪制自定義L1歸一化方法的數據的線條圖
for idx, col in enumerate(data_normalized_sklearn_l1.columns):plt.plot(data.index, data_normalized_sklearn_l1[col], linestyle='--', marker='x', linewidth=1, markersize=3)# 添加圖例、標題和坐標軸標簽
plt.title('L1 Normalization')
plt.xlabel('Index')
plt.ylabel('Normalized Value')# 顯示圖形
plt.tight_layout()
plt.show()

運行結果如下：

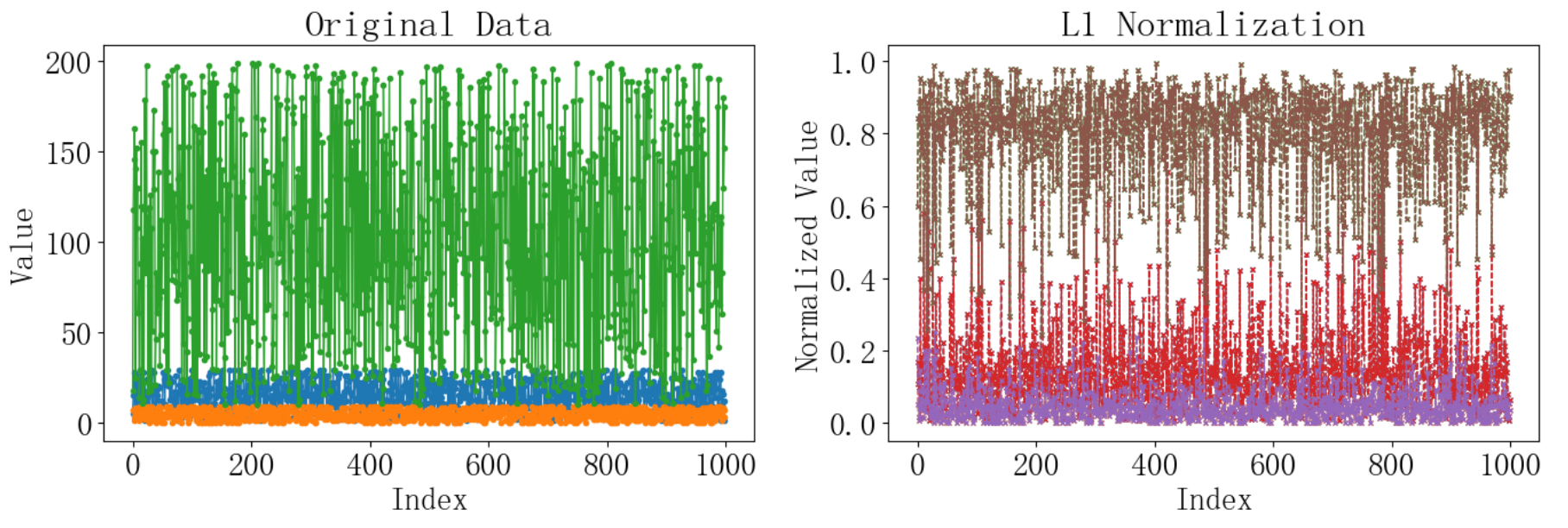
5 L2歸一化

L2歸一化，也稱為歐幾里得歸一化或2-范數歸一化，是一種將數據的特征向量按其平方和的平方根進行歸一化的方法。其目的是將每個特征的平方和除以向量的歐幾里得范數，使得每個特征向量的范數為1。L2歸一化在許多機器學習算法中很有用，特別是在需要考慮距離度量時，例如在K近鄰（KNN）算法中。

L2歸一化的公式為：

其中：x?是原始數據向量，′x′?是歸一化后的數據向量。∑x2?是向量x中所有元素平方的總和。

L2歸一化的優點包括：

它對數據的每個維度賦予了相等的重要性，因為它是基于向量的歐幾里得距離。
它在處理需要考慮角度和方向的應用中有廣泛的應用，如在圖像識別和計算機視覺中。

示例程序將使用兩種方法實現，自定義的L2歸一化封裝函數，并使用scikit-learn庫中的Normalizer類作為第二種方法來實現歸一化。以下是具體的實現：

方法1：自定義的L2歸一化歸一化封裝函數

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import Normalizer# 使用自定義函數進行L2歸一化
def l2_normalization(data):if isinstance(data, (pd.Series, pd.DataFrame)):norms = np.sqrt(np.sum(data**2, axis=1))data_normalized = data.div(norms, axis=0)return data_normalizedelse:raise ValueError("Input data must be a pandas Series or DataFrame")# 使用自定義函數進行L2歸一化
data_normalized_custom = l2_normalization(data.iloc[:, 7:10])

方法2：?`scikit-learn`庫中的`Normalizer`

# 使用 scikit-learn 的 Normalizer 進行L2歸一化
normalizer = Normalizer(norm='l2')
data_normalized_sklearn_l2 = normalizer.fit_transform(data.iloc[:, 7:10])
data_normalized_sklearn_l2 = pd.DataFrame(data_normalized_sklearn_l2, columns=data.columns[7:10])

# 繪制原始數據和歸一化數據的對比圖
plt.figure(figsize=(14, 5))plt.subplot(1, 2, 1)
# 繪制原始數據的線條圖
for idx, col in enumerate(data.columns[7:10]):plt.plot(data.index, data[col], label=f'Original {col}', marker='o', linewidth=1, markersize=3)plt.title('Original Data')
plt.xlabel('Index')
plt.ylabel('Value')plt.subplot(1, 2, 2)
# 繪制自定義L2歸一化方法的數據的線條圖
for idx, col in enumerate(data_normalized_custom.columns):plt.plot(data.index, data_normalized_custom[col], linestyle='--', marker='x', linewidth=1, markersize=3)# 繪制 scikit-learn L2歸一化方法的數據的線條圖
for idx, col in enumerate(data_normalized_sklearn_l2.columns):plt.plot(data.index, data_normalized_sklearn_l2[col], linestyle='-.', marker='s', linewidth=1, markersize=3)# 添加圖例、標題和坐標軸標簽
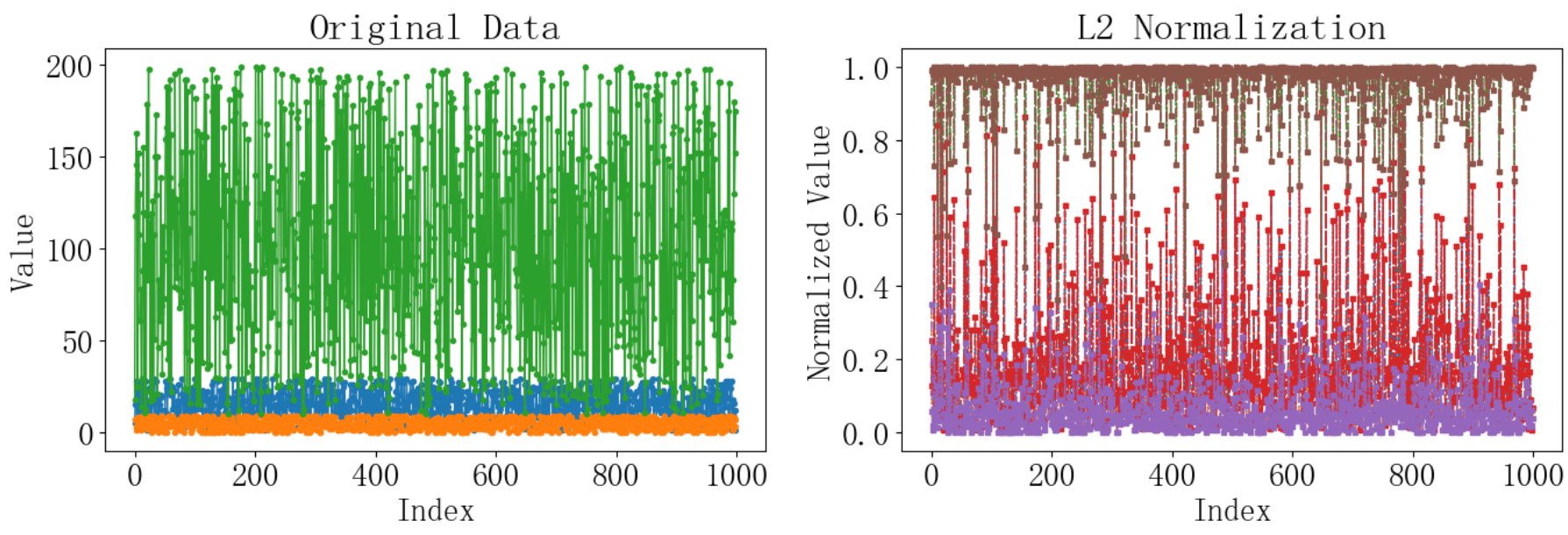
plt.title('L2 Normalization')
plt.xlabel('Index')
plt.ylabel('Normalized Value')# 顯示圖形
plt.tight_layout()
plt.show()

運行結果如下：

6?Box-Cox歸一化

Box-Cox歸一化是一種用于變換數據的分布，使其更接近正態分布的方法。它特別適用于處理具有偏態分布的數據，能夠減少數據的偏斜性并穩定方差。Box-Cox變換是一種冪律變換，可以表示為：

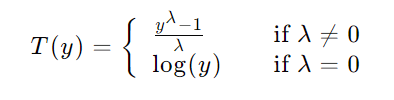
其中，y 是原始數據，λ 是變換參數。

Box-Cox歸一化的關鍵步驟包括：

選擇合適的變換參數?λ。這通常通過最大化變換后數據的似然函數來實現。
應用變換公式，根據選定的?λ?對數據進行變換。

Box-Cox歸一化的優點包括：

它能夠處理正值數據的偏態分布問題。
它可以減少數據的偏斜性，使數據更接近正態分布。
它可以穩定方差，使方差與均值無關。

示例程序將使用兩種方法實現，自定義的L2歸一化封裝函數，并使用scipy的boxcox作為第二種方法來實現歸一化。以下是具體的實現：

方法1：自定義的L2歸一化歸一化封裝函數

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 自定義Box-Cox歸一化函數
def custom_boxcox(data, lam):if lam == 0:return np.log(data)else:return (np.power(data, lam) - 1) / lam# 選擇Box-Cox變換的參數lambda，這里我們先假設為0.5（可以根據數據調整）
lambda_value = 0.5# 為每一列分別使用自定義Box-Cox歸一化函數
data_normalized_custom = pd.DataFrame()
for col_name in data.iloc[:, 7:10].columns:data_col = data[col_name] + 1  # 確保數據為正數，這里加1進行平移data_normalized_custom[col_name] = custom_boxcox(data_col, lambda_value)

方法2：?`scipy庫的boxcox`

from scipy import stats# 使用scipy的boxcox進行歸一化
data_normalized_scipy, lambda_selected = stats.boxcox(data.iloc[:, 7] + 1)

# 繪制原始數據和歸一化數據的對比圖
plt.figure(figsize=(14, 5))plt.subplot(1, 2, 1)
# 繪制原始數據的線條圖
for idx, col_name in enumerate(data.columns[7:10]):plt.plot(data.index, data[col_name], marker='o', linewidth=1, markersize=3)plt.title('Original Data')
plt.xlabel('Index')
plt.ylabel('Value')plt.subplot(1, 2, 2)
# 繪制自定義Box-Cox歸一化方法的數據的線條圖
for idx, col_name in enumerate(data_normalized_custom.columns):plt.plot(data.index, data_normalized_custom[col_name], linestyle='--', linewidth=1, markersize=3)# 繪制scipy Box-Cox歸一化方法的數據的線條圖
plt.plot(data.index, data_normalized_scipy, linestyle='-.', linewidth=1, markersize=3)# 添加圖例、標題和坐標軸標簽
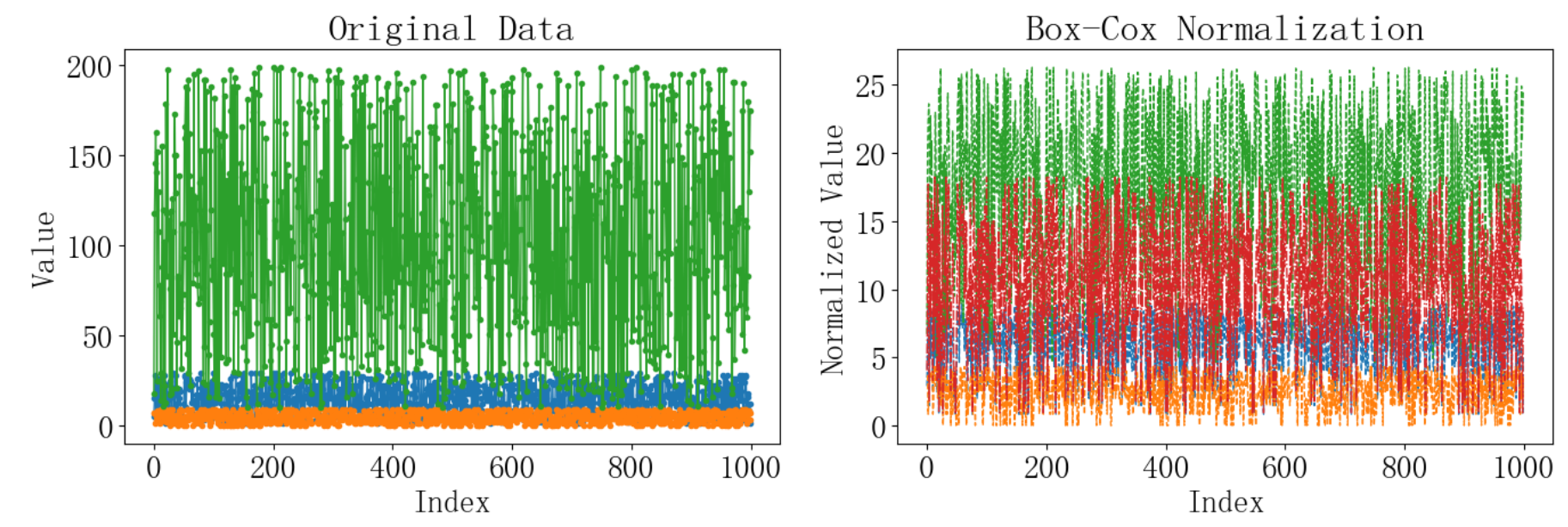
plt.title('Box-Cox Normalization')
plt.xlabel('Index')
plt.ylabel('Normalized Value')# 顯示圖形
plt.tight_layout()
plt.show()

運行結果如下：?

7 選擇哪種歸一化

各種歸一化方法各有其特點和適用場景，以下是它們的使用場景和優缺點的對比：

歸一化方法	特點
Min-Max歸一化	優點：可以指定數據變換后的范圍。缺點：對異常值敏感，因為最大值和最小值會受其影響。
Z-score歸一化	優點：降低了異常值的影響。缺點：數據必須有明確的均值和方差。
最大值歸一化	優點：可以處理非正態分布的數據。缺點：對數據中的零值和負值不敏感，如果數據集中的最大值很少變化，可能導致歸一化效果不佳。
L1歸一化	優點：能夠產生稀疏表示，對異常值有一定的魯棒性。缺點：可能導致數據的某些特征被忽略，特別是當這些特征的絕對值較小時。
L2歸一化	優點：考慮了特征的相對大小，有助于保留數據的幾何結構，常用于距離度量和聚類算法。缺點：對異常值敏感，計算相對復雜。
Box-Cox歸一化	優點：可以處理正值數據的偏態分布，通過變換參數λ調整，可以找到最佳的數據分布。缺點：需要選擇合適的λ值，這可能需要多次嘗試，對數據中的零值或負值不適用。