1. 矩陣置零
- 題目描述
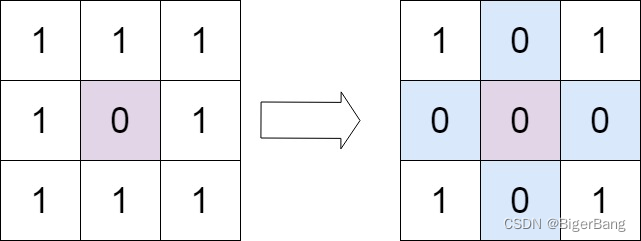
給定一個 m x n 的矩陣,如果一個元素為 0 ,則將其所在行和列的所有元素都設為 0 。請使用 原地 算法。
- 解題思路
題目要求進行原地更改,也就是不能使用額外的空間,因此我們可以使用第一行的元素來記錄對應的每一列是不是該置零,用第一列的元素來記錄對應的每一行是不是該置零。但是這樣的話就會有一個問題,就是第一行和第一列的元素會被覆蓋,因此我們在覆蓋第一行和第一列的元素前,需要額外的兩個變量row_0_flag和col_0_flag來記錄第一行和第一列是不是該置零。
時間復雜度:O(m*n) 空間復雜度:O(1) - 代碼
class Solution:def setZeroes(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""m = len(matrix)if m == 0:return n = len(matrix[0])# 在使用第一行和第一列進行記錄之前,先把第一行和第一列是否需要置零給求出來row_0_flag = Falsefor i in range(n):if matrix[0][i] == 0:row_0_flag = Truebreakcol_0_flag = Falsefor i in range(m):if matrix[i][0] == 0:col_0_flag = Truebreak# 使用第一行和第一列進行記錄for i in range(1, m):for j in range(1, n):if matrix[i][j] == 0:matrix[i][0] = 0matrix[0][j] = 0for i in range(1, m):for j in range(1, n):if (matrix[i][0] == 0 or matrix[0][j] == 0) and matrix[i][j] != 0:matrix[i][j] = 0if row_0_flag:for i in range(n):matrix[0][i] = 0if col_0_flag:for i in range(m):matrix[i][0] = 0
2. 螺旋矩陣
- 題目描述
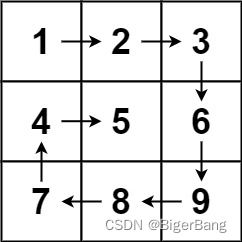
給你一個 m 行 n 列的矩陣 matrix ,請按照 順時針螺旋順序 ,返回矩陣中的所有元素。
- 解題思路
- 首先確認螺旋的圈數,圈數是(min(m, n) + 1) // 2,也就是最外層的循環數。
- 在每一圈中,我們需要分別從左到右,從上到下,從右到左,從下到上四個方向遍歷,在解題時可以現在紙上把每個方向遍歷的起始位置和終止位置寫出來,這樣就很容易寫出代碼。
- 注意在從右往左、從下到上遍歷的時候,要判斷是不是和從左往右、從上往下是不是一行,是一行的話就不用遍歷了。
時間復雜度:O(m*n) 空間復雜度:O(1)
- 代碼
class Solution:def spiralOrder(self, matrix: List[List[int]]) -> List[int]:m = len(matrix)n = len(matrix[0])iters = (min(m, n) + 1) // 2res = []for i in range(iters):# 從左往右打印for j in range(i, n - i):res.append(matrix[i][j])# 從上往下打印for j in range(i + 1, m - i):res.append(matrix[j][n - 1 - i])# 從右往左打印,此時要判斷是不是和從左往右打印的是一行,是一行的話很明顯就不用打印了if m - i - 1 > i:for j in range(n - 2 - i, i - 1, -1):res.append(matrix[m - i - 1][j])# 從下往上打印,此時要判斷是不是和從上往下打印是一列,是一列的話很明顯就不用打印了if i < n - 1 - i:for j in range(m - i - 2, i, -1):res.append(matrix[j][i])return res
3. 旋轉圖像
-
題目描述
給定一個 n × n 的二維矩陣 matrix 表示一個圖像。請你將圖像順時針旋轉 90 度。你必須在 原地 旋轉圖像,這意味著你需要直接修改輸入的二維矩陣。請不要 使用另一個矩陣來旋轉圖像。
-
解題思路
先轉置,再左右鏡像 -
代碼
class Solution:def rotate(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""n = len(matrix)# 轉置for i in range(n):for j in range(i + 1, n):matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]# 左右鏡像for i in range(n):l, r = 0, n - 1while l < r:matrix[i][l], matrix[i][r] = matrix[i][r], matrix[i][l]l += 1r -= 1
4. 搜索二維矩陣 II
-
題目描述
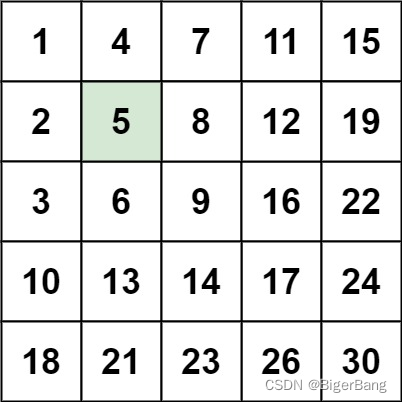
編寫一個高效的算法來搜索 m x n 矩陣 matrix 中的一個目標值 target 。該矩陣具有以下特性:每行的元素從左到右升序排列。
每列的元素從上到下升序排列。
-
解題思路
二分查找:從左上角開始搜索,小于target的話向下查找,大于target的話向左查找 -
代碼
class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:m = len(matrix)n = len(matrix[0])i = 0j = n - 1while i < m and j >= 0:if matrix[i][j] == target:return Trueelif matrix[i][j] > target:j -= 1else:i += 1return False









函數詳解:能給萬物排序的神奇函數)




- 一元線性回歸模型)


)

