基礎知識

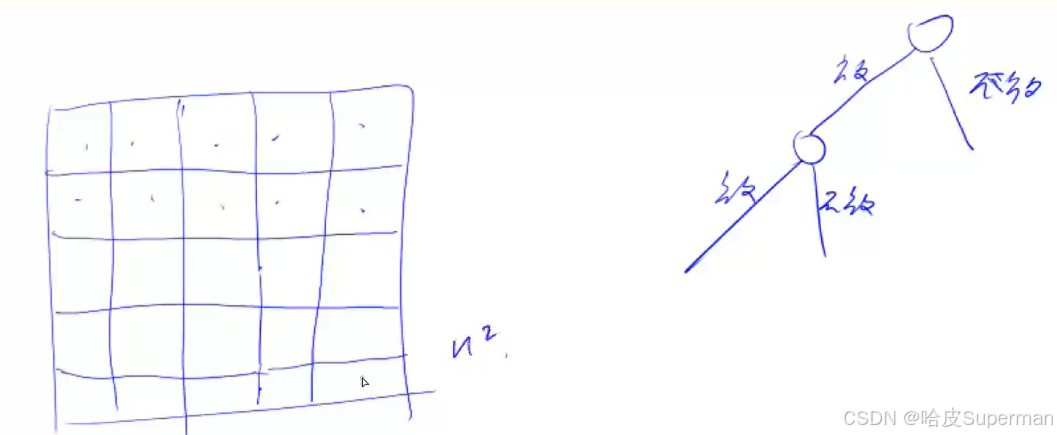
核心原理：一條路走到黑

示意圖：其含義表示，在這個圖中頂層是第0層，也就是后面dfs的入口，一般從dfs(0)開始操作。

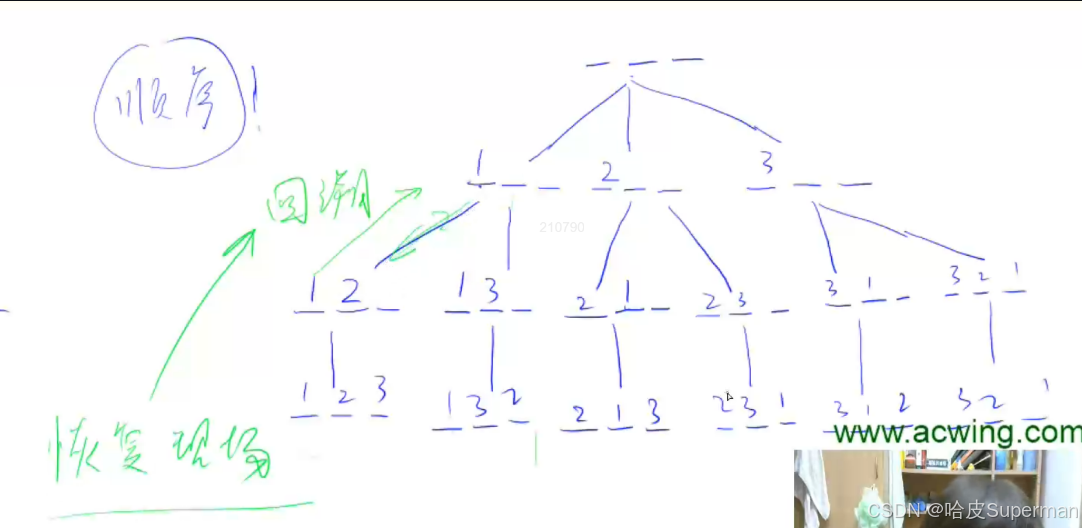
模版：

#include <iostream>using namespace std;/*** DFS* 給定一個整數 n，將數字 1～n* 排成一排，將會有很多種排列方法。* 現在，請你按照字典序將所有的排列方法輸出。*/const int N = 10;
int n;
int path[N];    // 路徑
bool st[N];     // 元素是否訪問過void dfs(int u){// 當前記錄的數字個數到達n層 可以輸出一種情況了if (u == n){for (int i = 0; i < n; i++){printf("%d ", path[i]);}printf("\n");}//還可以繼續dfs搜索 這里的i是放的數值 從1~n嘛for (int i = 1; i <= n; i ++){// 如果當前層沒有被使用過if(!st[i]){path[u] = i;     //假設當前層放數值i進行嘗試st[i] = true;    //標記訪問過了dfs(u + 1);      //繼續下一層// 一定要恢復現場st[i] = false;}}
}int main(){cin >> n;dfs(0);  //從頂層也就是第0層開始return 0;
}

典型例題

例1：n皇后問題

非常經典的問題，指將n個皇后放在n * n的國際象棋棋盤上，任意兩個皇后不能處于同一行、同一列或同一斜線上。

我們的策略是一行一行的試，比如在第一行的時候，我們嘗試把第一個皇后放在所有列上的后續情況全部嘗試一邊，注意在這個過程中如果遇到不符合題目的情況需要及時剪枝。

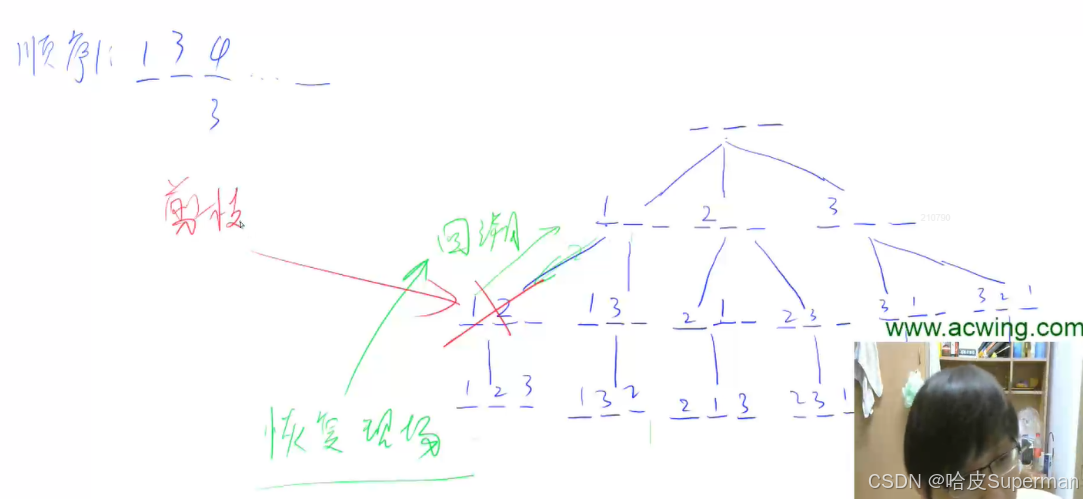
在判斷的過程中，除了行和列不能重復，最關鍵的是對角線的處理，這個分為對角線和反對角線，參考y = ax + b這條直線的截距進行理解

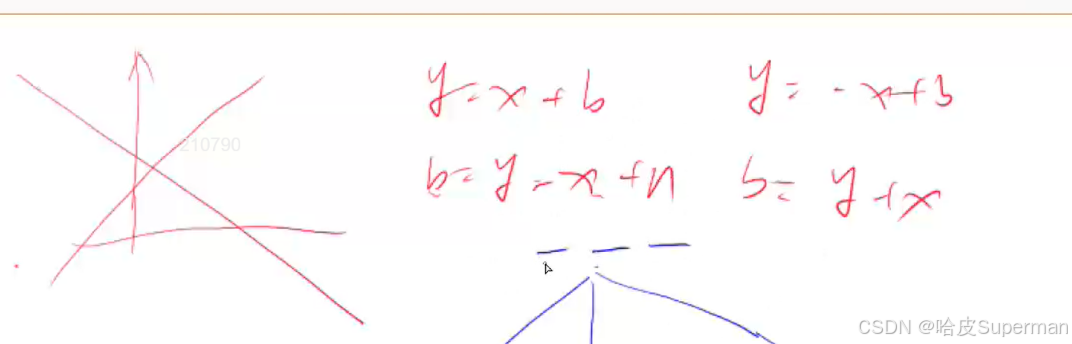
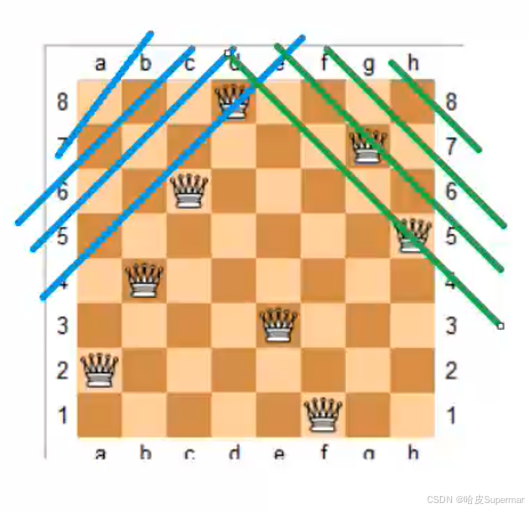
最終代碼：

#include <iostream>using namespace std;const int N = 20;
int n;
char g[N][N];   // 記錄方案 使用字符串記錄 
bool col[N], dg[N], udg[N];     // 標記  當前列是否放置過 當前對角線是否放置 當前反對角線是否放置 行不用考慮 因為dfs逐層下搜void dfs(int u){// 當前記錄的數字個數到達n層 可以輸出一種情況了if (u == n){for (int i = 0; i < n; i++){puts(g[i]);}printf("\n");}//還可以繼續dfs搜索 這里的i是放的列值 從0~n-1嘛   對角線怎么設置的for (int i = 0; i < n; i ++){// 如果當前列 對角線 反對角線沒有被使用過if(!col[i] && !dg[u + i] && !udg[n - u + i]){g[u][i] = 'Q';     //假設當前行u 的第i列可以放置col[i] = dg[u + i] = udg[n - u + i] = true;    //標記訪問過了  注意對角線dfs(u + 1);      //繼續下一層// 一定要恢復現場col[i] = dg[u + i] = udg[n - u + i] = false;g[u][i] = '.';}}
}int main(){cin >> n;for (int i = 0; i < n; i ++){for (int j = 0; j < n; j++){g[i][j] = '.';}}dfs(0);  //從頂層也就是第0層開始return 0;
}

方法2：每一個格子進行枚舉

這個的思想就是每個格子都嘗試一下能不能放皇后，遍歷所有情況。

#include <iostream>using namespace std;const int N = 20;
int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N];// x 是行  y是列 s是當前擺下的皇后的個數
void dfs(int x, int y, int s){if (y == n){// 越界后 直接切換到下一行的第一個位置x ++;y = 0;}if (x == n){if (s == n){//完全擺完了 可以進行輸出for (int i = 0; i < n; i ++){puts(g[i]);}printf("\n");}return;   //這里一定要記得return 因為還沒完全結束所有情況}//正常走到這個格子了 下面就兩種操作 一個是放皇后 一個是不放// 嘗試不放 直接下一個// dfs(x, y ++, s);  這里太嚇人了  一定不能用這種自增 要不然就死循環了dfs(x, y + 1, s);// 嘗試放皇后 需要看能否放if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]){g[x][y] = 'Q';row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;// 下一個// dfs(x, y ++, s ++);dfs(x, y + 1, s + 1);// 恢復現場row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;g[x][y] = '.';}}int main(){cin >> n;for (int i = 0; i < n; i ++){for (int j = 0; j < n; j ++){g[i][j] = '.';}}// 0行 0列 也就是第一個格子  當前放置的皇后數為0；dfs(0, 0, 0);return 0;
}

例2：拍照

題面：小 A、小 B、小 C、小 D、小 E 五個人 拍照，我們會輸入一些前提條件，當id為1的時候，表示后面跟的兩個字母對應的人需要相鄰，id為2的時候，后面跟的兩個字母對應的人需要相隔，最終輸出多少種拍照方案

思考轉換：

轉換為dfs進行求解，就是把這5個人進行排序，比如先嘗試把A放在第一個位置，后面嘗試所有站位可能，在這個過程中，我們需要借助限制選項，比如相鄰還是相隔，可以實現提前剪枝，如果當前的站位方案不符合限制條件，也就是過不了我們的check函數，就直接剪掉。

最終代碼：

#include <iostream>using namespace std;/*** 小 A、小 B、小 C、小 D、小 E 五個人 * 轉換成dfs 就相當于5個人排位置  只不過添加了一些限制條件 進行剪枝*/// 整個結構體
struct limit{int id;char x, y;
}a[100];int res;
bool vis[105];
int path[1005];
int m;bool check(){// 遍歷檢查限制for (int i = 0; i < m; i ++){int id = a[i].id, x = a[i].x - 'A' + 1, y = a[i].y - 'A' + 1;// 這里一定要分清 位置和人物標號的關系int posx = 0, posy = 0;for (int i = 1; i <= 5; i ++){if (path[i] == x){posx = i;}if (path[i] == y){posy = i;}}// 這是要相鄰if (id == 1){// 思考 path[x] 代表的含義 我們應該找出第x個人所在的位置if (abs(posx - posy) > 1){return false;  //沒有相鄰}}// 必須不能相鄰if (id == 2){if (abs(posx - posy) == 1){return false;  //沒有相鄰}}}return true;
}
void dfs(int x){if (x == 5){if (check()){res ++;}   return;   // 當前結束，方案可能有多種，直接回退測試下一個方案}// 嘗試著5個人都放在當前位置for (int i = 1; i <= 5; i ++){if (!vis[i]){path[x] = i;   // 第x這個位置 放在第i個人vis[i] = true;dfs(x + 1);vis[i] = false;}}}int main(){cin >> m;for (int i = 0; i < m; i ++){cin >> a[i].id >> a[i].x >> a[i].y;}dfs(0);  // 從頂層 也就是第0層開始cout << res;return 0;
}

例3：理發

題面：

思考轉換：這個轉換的思路在于選定一個標準進行dfs，因為先進行洗頭，所有人都要先洗頭，我們就把洗頭的順序作為dfs執行的標準，嘗試所有顧客開始洗頭的順序，洗頭確定之后，可以覆蓋所有組合情況，后面剪頭就只能按照實際情況進行，不斷更新記錄用時最短的方案。

最終代碼：

#include <iostream>
#include <queue>using namespace std;const int N = 11;
int a[N], b[N];  //洗發和剪發
int n;
int res = 1e9;   
int path[1005];
bool vis[105];// 首先可以明白 我們dfs的對象是什么 是洗頭的順序安排剩下的剪頭只能被迫安排
void dfs(int x){if (x == n){int y1 = 0, y2 = 0;   // 洗頭順序固定的情況下 尋找最短總時間priority_queue<int> q;for (int i = 0; i < n; i ++){int peo = path[i];  //第i個人y1 += a[peo];         // 第i個人洗發// 剪發時間 進入優先隊列q.push(b[peo]);y2 = max(y2, y1);  // y2是擔心之前還有人沒剪完頭int w = q.top();    //剪發 讀隊中頭 自動排序 最大的  讀完pop出隊q.pop();        y2 += w;   }res = min(y2, res);return;}for (int i = 0; i < n; i ++){if (!vis[i]){vis[i] = true;path[x] = i;   // 誰都有機會放在第一個 dfs(x + 1);vis[i] = false;}}
}int main(){int t;cin >> t;while (t --){cin >> n;res = 1e9;for (int i = 0; i < n; i ++){cin >> a[i] >> b[i];}dfs(0);cout << res << endl;}return 0;
}