隨機森林算法詳細介紹
1. 理論背景
隨機森林(Random Forest)是一種由Leo Breiman和Adele Cutler在2001年提出的集成學習方法。它結合了多個決策樹的預測結果,以提高模型的準確性和魯棒性。
2. 算法細節
隨機森林的構建過程可以分為以下幾個步驟:
-
Bootstrap采樣:從原始數據集中隨機選擇樣本,有放回地生成多個子樣本集(即每個子樣本集中可能包含重復的樣本)。
-
決策樹構建:對每個子樣本集構建一個決策樹。在構建每棵決策樹時,對每個節點選擇的特征是從所有特征中隨機選取的子集。
-
集成預測:對分類任務,通過對所有決策樹的投票結果進行多數投票來確定最終的分類結果。對回歸任務,通過對所有決策樹的預測結果取平均值來確定最終的回歸結果。
3. 算法優點
-
減少過擬合:通過對多個決策樹的結果進行平均或投票,減少了單棵決策樹過擬合的風險。
-
高準確率:由于結合了多個模型的預測結果,通常比單獨的決策樹模型具有更高的預測準確性。
-
處理高維數據:能夠處理含有大量特征的數據,并能有效地進行特征選擇。
-
抗噪聲能力強:由于集成了多個決策樹的結果,對噪聲數據具有較好的魯棒性。
Python實現與可視化示例
下面是一個詳細的Python示例,展示如何使用隨機森林算法進行泰坦尼克號數據集的分類任務。泰坦尼克號數據集(Titanic Dataset)是機器學習領域中常用的經典數據集之一,廣泛用于分類模型的訓練和測試。這個數據集記錄了泰坦尼克號1912年沉船事故中的乘客信息和他們的生還情況。通過分析這些數據,機器學習模型可以預測某個乘客是否在事故中幸存。泰坦尼克號數據集通常包括以下幾個文件:train.csv:訓練數據集,用于模型訓練test.csv:測試數據集,用于模型測試;gender_submission.csv:提交格式示例,展示提交預測結果的格式。
數據集中包含多個特征,每個特征描述了乘客的不同方面:
-
PassengerId:乘客ID,唯一標識每個乘客。
-
Survived:生還情況(0 = 未生還,1 = 生還)。
-
Pclass:客艙等級(1 = 頭等艙,2 = 二等艙,3 = 三等艙)。
-
Name:乘客姓名。
-
Sex:性別(male = 男性,female = 女性)。
-
Age:年齡。
-
SibSp:在船上的兄弟姐妹/配偶數量。
-
Parch:在船上的父母/子女數量。
-
Ticket:船票號碼。
-
Fare:票價。
-
Cabin:客艙號。
-
Embarked:登船港口(C = Cherbourg, Q = Queenstown, S = Southampton)。
import?os
import?pandas?as?pd
import?numpy?as?np
import?matplotlib.pyplot?as?plt
import?seaborn?as?sns
from?sklearn.ensemble?import?RandomForestClassifier??#?導入隨機森林分類器
from?sklearn.model_selection?import?train_test_split??#?導入數據集劃分工具
from?sklearn.metrics?import?classification_report,?confusion_matrix,?roc_curve,?auc??#?導入評估工具
from?sklearn.preprocessing?import?LabelEncoder??#?導入標簽編碼器
from?sklearn.manifold?import?TSNE??#?導入t-SNE降維工具#?加載數據
train?=?pd.read_csv('Titanic_train.csv')??#?讀取訓練數據集
test?=?pd.read_csv('Titanic_test.csv')??#?讀取測試數據集#?數據預處理
def?preprocess_data(df):df['Age'].fillna(df['Age'].median(),?inplace=True)??#?填充缺失的年齡數據為中位數df['Embarked'].fillna(df['Embarked'].mode()[0],?inplace=True)??#?填充缺失的登船港口為眾數df['Fare'].fillna(df['Fare'].median(),?inplace=True)??#?填充缺失的票價為中位數df.drop(['Cabin',?'Ticket',?'Name'],?axis=1,?inplace=True)??#?刪除不必要的特征df['Sex']?=?LabelEncoder().fit_transform(df['Sex'])??#?將性別轉換為數值df['Embarked']?=?LabelEncoder().fit_transform(df['Embarked'])??#?將登船港口轉換為數值return?dftrain?=?preprocess_data(train)??#?預處理訓練數據
test?=?preprocess_data(test)??#?預處理測試數據#?特征和標簽
X?=?train.drop('Survived',?axis=1)??#?提取特征變量
y?=?train['Survived']??#?提取標簽變量#?數據集劃分
X_train,?X_test,?y_train,?y_test?=?train_test_split(X,?y,?test_size=0.3,?random_state=42)??#?將數據集劃分為訓練集和測試集#?隨機森林模型
clf?=?RandomForestClassifier(n_estimators=100,?random_state=42)??#?初始化隨機森林分類器
clf.fit(X_train,?y_train)??#?訓練模型#?預測
y_pred?=?clf.predict(X_test)??#?對測試集進行預測#?結果評估
print("Classification?Report:")
print(classification_report(y_test,?y_pred))??#?打印分類報告#?混淆矩陣
conf_matrix?=?confusion_matrix(y_test,?y_pred)??#?計算混淆矩陣
print("Confusion?Matrix:")
print(conf_matrix)??#?打印混淆矩陣#?特征重要性
importances?=?clf.feature_importances_??#?獲取特征重要性
indices?=?np.argsort(importances)[::-1]??#?按重要性排序
feature_names?=?X.columns??#?獲取特征名稱#?可視化特征重要性
plt.figure(figsize=(10,?6))
plt.title("Feature?Importances")
plt.bar(range(X.shape[1]),?importances[indices],?align="center")
plt.xticks(range(X.shape[1]),?[feature_names[i]?for?i?in?indices],?rotation=45)
plt.xlabel("Feature")
plt.ylabel("Importance")
plt.show()??#?顯示特征重要性圖#?ROC曲線
y_score?=?clf.predict_proba(X_test)[:,?1]??#?獲取預測概率
fpr,?tpr,?_?=?roc_curve(y_test,?y_score)??#?計算ROC曲線
roc_auc?=?auc(fpr,?tpr)??#?計算AUCplt.figure(figsize=(10,?6))
plt.plot(fpr,?tpr,?color='darkorange',?lw=2,?label='ROC?curve?(area?=?%0.2f)'?%?roc_auc)
plt.plot([0,?1],?[0,?1],?color='navy',?lw=2,?linestyle='--')
plt.xlim([0.0,?1.0])
plt.ylim([0.0,?1.05])
plt.xlabel('False?Positive?Rate')
plt.ylabel('True?Positive?Rate')
plt.title('Receiver?Operating?Characteristic')
plt.legend(loc="lower?right")
plt.show()??#?顯示ROC曲線#?t-SNE圖
tsne?=?TSNE(n_components=2,?random_state=42)??#?初始化t-SNE
X_tsne?=?tsne.fit_transform(X_test)??#?對測試集特征進行降維plt.figure(figsize=(10,?6))
scatter?=?plt.scatter(X_tsne[:,?0],?X_tsne[:,?1],?c=y_test,?cmap='viridis')??#?繪制t-SNE圖
plt.legend(*scatter.legend_elements(),?title="Classes")
plt.title("t-SNE?visualization")
plt.xlabel("t-SNE?component?1")
plt.ylabel("t-SNE?component?2")
plt.show()??#?顯示t-SNE圖#?輸出:
"""
Classification?Report:precision????recall??f1-score???support0???????0.81??????0.90??????0.85???????1571???????0.83??????0.70??????0.76???????111accuracy???????????????????????????0.82???????268macro?avg???????0.82??????0.80??????0.81???????268
weighted?avg???????0.82??????0.82??????0.81???????268Confusion?Matrix:
[[141??16][?33??78]]
"""
輸出結果分類報告中的各項指標包括精確率(precision)、召回率(recall)、F1分數(f1-score)和支持(support)。這些指標可以幫助我們全面評估模型的性能。
Classification?Report:precision????recall??f1-score???support0???????0.81??????0.90??????0.85???????1571???????0.83??????0.70??????0.76???????111accuracy???????????????????????????0.82???????268macro?avg???????0.82??????0.80??????0.81???????268
weighted?avg???????0.82??????0.82??????0.81???????268
各項指標解釋
-
精確率(Precision):
-
定義:精確率是正確預測的正樣本數占所有預測為正的樣本數的比例。
-
計算公式:Precision=TPTP+FPPrecision=TP+FPTP
-
解釋:模型在預測某一類(例如幸存者)時,預測正確的比例。對于0類(未幸存者),精確率是0.81;對于1類(幸存者),精確率是0.83。
-
-
召回率(Recall):
-
定義:召回率是正確預測的正樣本數占所有實際為正的樣本數的比例。
-
計算公式:Recall=TPTP+FNRecall=TP+FNTP
-
解釋:模型在預測某一類時,能夠正確識別的比例。對于0類,召回率是0.90;對于1類,召回率是0.70。
-
-
F1分數(F1-Score):
-
定義:F1分數是精確率和召回率的調和平均數。
-
計算公式:F1-Score=2×Precision×RecallPrecision+RecallF1-Score=2×Precision+RecallPrecision×Recall
-
解釋:F1分數綜合考慮了精確率和召回率,提供了一個平衡的性能評估。對于0類,F1分數是0.85;對于1類,F1分數是0.76。
-
-
支持(Support):
-
定義:支持是每個類別中的實際樣本數。
-
解釋:支持表示的是數據集中每個類別的樣本數。0類有157個樣本,1類有111個樣本。
-
整體性能指標
-
準確率(Accuracy):
-
定義:準確率是正確預測的樣本數占總樣本數的比例。
-
計算公式:Accuracy=TP+TNTP+TN+FP+FNAccuracy=TP+TN+FP+FNTP+TN
-
解釋:在所有樣本中,模型正確預測的比例。這里準確率是0.82(即82%的樣本被正確分類)。
-
-
宏平均(Macro Avg):
-
定義:宏平均是對各類別的指標進行簡單平均,不考慮類別的樣本數。
-
解釋:提供了各類別性能指標的整體平均值。這里宏平均的精確率是0.82,召回率是0.80,F1分數是0.81。
-
-
加權平均(Weighted Avg):
-
定義:加權平均是對各類別的指標按其樣本數進行加權平均。
-
解釋:考慮類別樣本數后的性能指標平均值。這里加權平均的精確率是0.82,召回率是0.82,F1分數是0.81。
-
混淆矩陣解釋
Confusion?Matrix:
[[141??16][?33??78]]
混淆矩陣顯示了實際標簽與預測標簽的對比。
-
第一行表示實際為0類(未幸存者)的樣本:
-
141:實際為0類且預測為0類(真正例,True Negative, TN)。
-
16:實際為0類但預測為1類(假陽性,False Positive, FP)。
-
-
第二行表示實際為1類(幸存者)的樣本:
-
33:實際為1類但預測為0類(假陰性,False Negative, FN)。
-
78:實際為1類且預測為1類(真陽性,True Positive, TP)。
-
特征重要性解釋
-
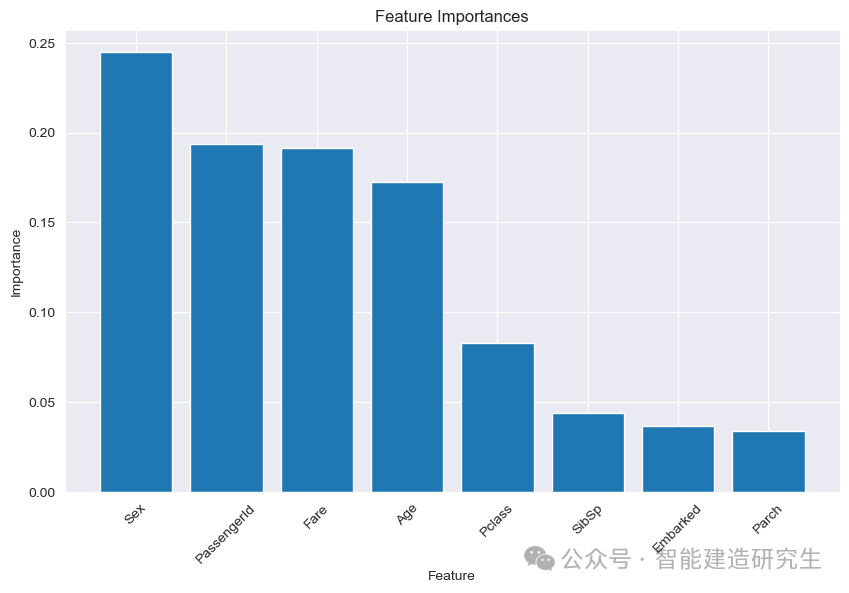
解釋:特征重要性圖顯示了每個特征在模型中的重要性。通過這個圖,我們可以看到哪些特征對模型的預測影響最大。對于泰坦尼克號數據集,性別(Sex)、乘客ID(PassengerId)、票價(Fare)和年齡(Age)可能是最重要的特征,因為這些因素在實際的生存情況中也是重要的。
-
重要性:這種可視化幫助我們理解模型的決策過程,并提供關于數據特征的重要性的信息。
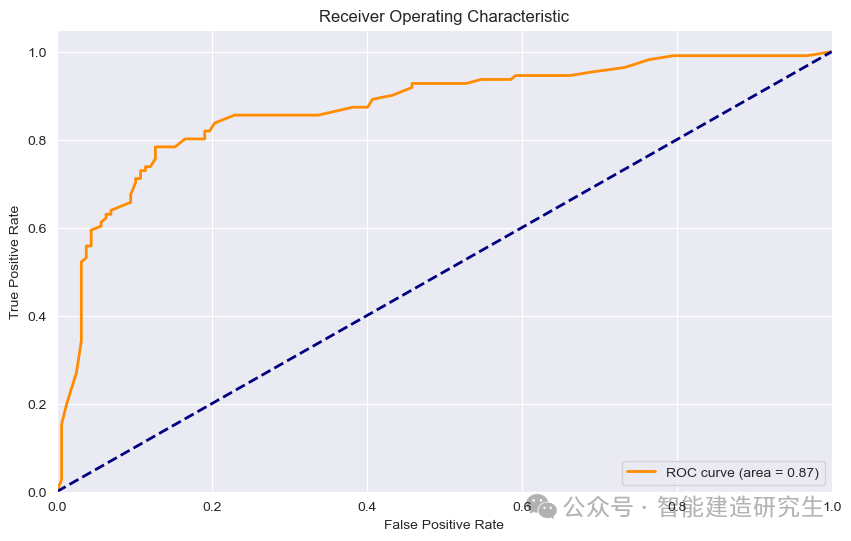
ROC曲線解釋
-
解釋:ROC(Receiver Operating Characteristic)曲線是評估分類模型性能的常用工具,特別是在不平衡數據集上。它展示了模型在不同閾值下的真陽性率(True Positive Rate, TPR)和假陽性率(False Positive Rate, FPR)之間的關系。曲線下的面積(AUC, Area Under Curve)用于量化模型的總體性能。
-
重要性:ROC曲線提供了一個整體的模型性能評估,特別是在不平衡數據集上,它可以展示模型在不同閾值下的表現。
-
模型性能良好:
-
該模型的AUC值為0.87,接近1,說明模型在區分泰坦尼克號數據集中幸存者和未幸存者時表現較好。
-
TPR較高,意味著模型能夠正確識別大部分幸存者(正樣本)。
-
t-SNE圖解釋
-
解釋:t-SNE圖是一種降維可視化方法,將高維數據投影到2維平面上。通過顏色表示不同類別的數據點(幸存者和未幸存者)。在泰坦尼克號數據集中,這可以幫助我們觀察數據在低維空間中的分布情況,查看數據是否存在明顯的聚類現象。
-
重要性:這種可視化有助于直觀理解數據的內在結構和模型的分類效果,特別是觀察不同類別之間的分離情況。
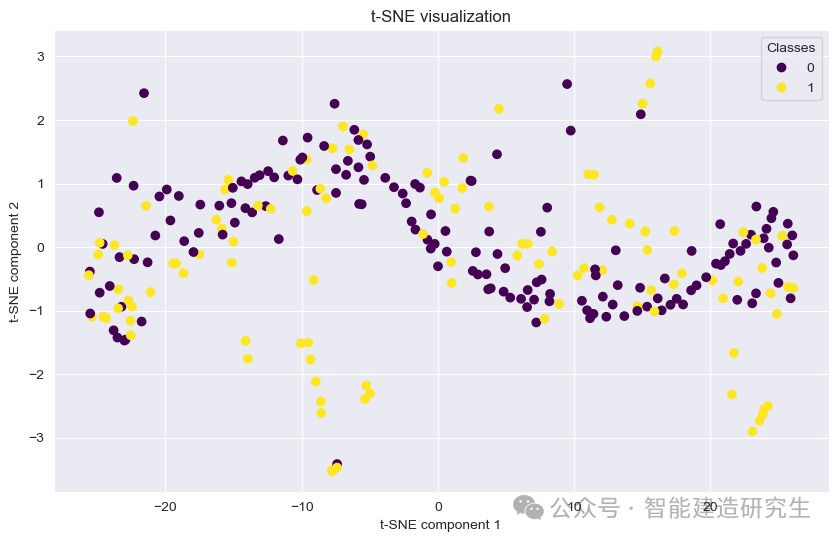
t-SNE將高維數據降維到2維空間,降維后的兩個維度不是原始數據中的特定維度,而是t-SNE算法通過保持高維數據的鄰近關系優化得到的兩個新維度。圖中黃色和紫色的點分別代表兩個類別,即幸存者(1)和未幸存者(0)。
從整體上看,幸存者(黃色點)在t-SNE圖中分布較為分散,而未幸存者(紫色點)則在一些特定區域集中。這可能與泰坦尼克號數據集中某些關鍵特征(如性別、艙位等級、年齡等)有關,這些特征對生存概率有顯著影響。
以上內容總結自網絡,如有幫助歡迎轉發,我們下次再見!
:界面優化)
![[Go 微服務] Kratos 使用的簡單總結](http://pic.xiahunao.cn/[Go 微服務] Kratos 使用的簡單總結)






)
新政)
服務端包含 合并拼裝靜態內容)





歐幾里得、DES、RSA、SHA-1算法)


