數據結構_線性表

?線性表的定義和特點

線性表是具有相同特性的數據元素的一個有限序列

$(a_{1},a_{2},a_{3},......a_{i-1},a_{i},a_{i+1},....a_{n})$

$a{_{1}}$ :線性起點/起始節點

$a_{i-1}$ ?: $a_{i}$ 的直接前驅

$a_{i+1}$ ?: $a_{i}$ 的直接后繼

$a_{n}$ :線性終點/終端節點

n:元素總個數,表長

下標:是元素的序號,表示元素在表中的位置

n=0時稱為空表

線性表

由n(n>0)個數據元素(結點), $a_{1},a_{2},...a_{n}$ 組成的有限序列

將非空的線性表(n>0)記作:( $a_{1},a_{2},...a_{n}$ )

這里的數據元素 $a_{i}$ ( $1\leq i\leq n$ )只是一個抽象的符號,其具體含義在不同的情況下,可以不同

例1

分析26個英文字母組成的英文表

? ? ? ? (A,B,C...Z)

數據元素都是字母,元素間關系是線性關系

例2

分析學生情況登記表

略

每條記錄也是線性關系

例3

某單位歷年擁有計算機的數量(4,6,45,34,33) 線性關系(先后)

例4?

12星座 (白羊座,金牛座,...雙魚座) 線性關系(先后)

同一線性表的元素必定有相同特性,數據元素之間的關系是線性關系

綜上線性表的邏輯特征是:
在非空的線性表中,有且一個開始節點 $a_{1}$ ,它沒有直接前趨,僅有一個后繼 $a_{2}$

在非空的線性表中,有且一個終端節點 $a_{n}$ ,它沒有直接后繼,僅有一個前趨 $a_{n-1}$

其余節點 $a_{i}$ ( $2\leq i\leq n-1$ ) 僅有一個前趨 $a_{i-1}$ ,僅有一個后繼 $a_{i+1}$

線性表是一種典型的線性結構

線性表案例

例1

一元多項式的運算:實現兩個多項式加,減,乘運算

$P_{n}(x) = p_{0} + p_{1}x + p_{2}x^{2} + ... + p_{n}x^{n}$

線性表P=( $p_{0},p_{1},p_{2},...,p_{n}$ )

每一項的指數i隱含在其系數 $p_{i}$ 的序號中

用數組來表示

$P(x) = 10 + 5x - 4x^{2} + 3x^{3} + 2x^{4}$

指數用下標表示,系數用具體值表示

操作

兩個多項式相加

$R_{n}(x) = P_{n}(x) + Q_{m}(x)$

線性表R? = ( $p_{0} + q_{0},p_{1} + q_{1},p_{2} + q_{2},...p_{n} + q_{m...}$ )

例2:稀疏多項式

$S(x) = 1 + 3x^{10000} + 2x^{20000}$

如果用前面下標代表指數,會造成空間浪費

多項式非零項的數組表示

$A(x) = 7 + 3x + 9x^{8} + 5x^{17}$

$B(x) = 8x + 22x^{7} - 9x^{8}$

線性表?? $P = ((p1,e1),(p2,e2),(p3,e3),....(pm,em))$

線性表A=((7,0),(3,1),(9,8).(5,17))

線性表B=((8,1),(22,7),(-9,8))

創建一個新數組c

分別從頭遍歷比較a和b的每一項

指數相同,對應系數相加,若其和不為0,則在c中加一個新項

指數不相同,則將指數較少的項復制到c中

一個多項式遍歷完畢時,將另一個剩余項依次復制到c即可

缺陷:并不知道數組c的空間要分配多少

順序存儲結構存在問題

存儲空間分配不靈活

運算的空間復雜度高(需要額外的空間)

解決問題

鏈式存儲結構?后續詳細介紹

例3:圖書信息管理系統

需要的功能: 增(插入)刪改查排序計數

圖書表抽象為線性表

表中每本書抽象成線性表中的數據元素

圖書順序表:數組存儲

圖書鏈表:鏈表存儲

選擇適當的存儲結構

實現此存儲結構上的基本操作

利用基本操作完成功能

總結:

線性表中數據元素的類型可以為簡單類型,也可以為復雜類型

許多實際應用問題所涉及的基本操作有很大相似性,不應為每個具體應用單獨編寫一個程序

從具體應用中抽象出共性的邏輯結構和基本操作(抽象數據類型),然后實現其存儲結構和基本操作

線性表的類型定義

抽象數據類型線性表的定義如下:

ADT List{

? ? ? ? 數據對象: D = {? ? $a_{i} | a_{i}$ 屬于Elemset, $(i=1,2,....,n,n\geq 0)$ ??}

? ? ? ? 數據關系: R = {? $<a_{i-1},a_{i}> | a_{i-1},a_{i}$ ?屬于 $D_{i}$ ?(i=2,3,....n)}

? ? ? ? 基本操作:

????????????????InitList(&L)

? ? ? ? 略

} ADT List

基本操作:

初始化線性表

InitList(&L)

操作結構:構造一個空的線性表L

銷毀線性表

DestroyList(&L)

初始條件:線性表L已經存在

操作結果:銷毀線性表L

清除線性表

ClearList(&L)

初始條件:線性表L已經存在.

操作結果:將線性表L重置為空表

判斷線性表是否為空

ListEmpty(L)

初始條件:線性表L已經存在

操作結果:若線性表L為空表,則返回Ture,否則返回False

返回線性表L的元素個數

ListLlenth(L)

初始條件:線性表L已經存在

操作結果:返回線性表L中的數據元素個數

返回線性表第i個元素的值

GetElem(L,i,&e);

初始條件:線性表L已經存在,1<=i <= ListLenth(L)

操作結果:用e 返回線性表L中第i個元素的值

返回L中第1個與e滿足compare()的數據元素的位序

LocateElem(L,e,compare())

初始條件:線性表L已經存在,compare()是數據元素判定函數

操作結果:返回L中第1個與e滿足compare()的數據元素的位序,若這樣的數據元素不存在則返回值為0.

待補充

忘保存，明天補上

線性表的順序表示和實現2

順序表的特點：

以物理位置相鄰表示邏輯關系

任一元素均可隨機存取（優點）

用高級語言實現數據類型

用一維數組表示順序表

線性表可變（刪除）

數組長度不可動態定義

注:一維數組的定義方式

類型說明符數組名[常量表達式]

說明:常量表達式中可以包含常量和符號常量,不能包含變量,, 即C語言中不允許對數組的大小做動態定義

解決方式:用一變量表示順序表的長度屬性

如下所示

c定義結構體

#define LIST_INIT_SIZE 100 
//線性表存儲空間的初始分配量
//定義了一個結構體 ?SqList?，包含一個數組和一個整型變量 
typedef struct { Elem Type elem[LIST_INIT_SIZE];int length; //當前長度
} SqList;

實例

多項式的順序存儲結構類型定義

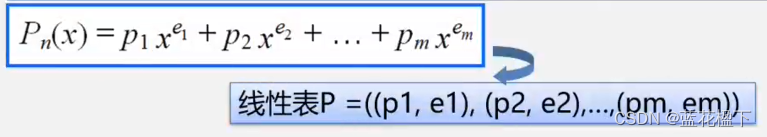
c實現

#define MAXSIZE 1000
//多項式可能達到的最大長度//結構體：多項式非零項定義
typedef struct {float p; //系數int e; //指數
} Polynomial;//結構體:多項式順序存儲結構
typedef struct{Polynomial *elem; //基地址int length; //當前項個數
} SqList;

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/39718.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/39718.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/39718.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！