書接上文，我們講完了哈代溫伯格基因型頻率，也使用數據進行了擬合，那么接下來就是考慮一些計算的問題：

【基于R語言群體遺傳學】-1-哈代溫伯格基因型比例-CSDN博客

【基于R語言群體遺傳學】-2-模擬基因型（simulating genotypes）-CSDN博客

如果我們有群體樣本中個體的基因型，那么我們不需要假設哈代-溫伯格比例來從表型頻率估計等位基因頻率。我們可以簡單地計數等位基因。每個雜合子有一個等位基因的拷貝，而純合子有兩個拷貝（再次假設是一個二倍體生物）。由于每個采樣的個體在每個位點都有兩個拷貝，所以觀察到的等位基因總數是采樣個體數量的兩倍。

然后，我們可以通過將雜合子的數量加上純合子數量的兩倍（因為每個純合子有兩個等位基因的拷貝），然后除以采樣個體數量的兩倍（因為每個采樣的個體攜帶兩個位點），來計算特定等位基因的頻率：

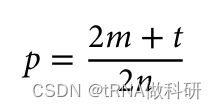
哈代溫伯格假設

為了得到p2 + 2pq + q2并運行這里用來說明期望的模擬，我們做了以下假設：

? 被考慮的有機體是二倍體。

? 被考慮的有機體僅通過性繁殖（無克隆）。

? 不存在具有不同等位基因頻率的獨立種群，無論它們之間是否有遷移。

? 我們所考慮的種群在大小上是無限大的。

? 所有交配都是隨機發生的。

? 沒有遺傳變異受到自然選擇的影響（等位基因的生存和繁殖差異）。

? 沒有遺傳變異因突變而丟失或獲得（沒有等位基因突變為新的等位基因）。

? 世代之間不重疊。一旦繁殖發生，所有的親本消失，只有產生的后代貢獻給下一代。

顯然，這些期望在生物學上并不非常現實。然而，哈代-溫伯格期望對大多數這些假設的違反都相當穩健，除了前三個：單倍體或多倍體有機體必須以不同但合理的方式處理，通過無性繁殖的有機體可能與哈代-溫伯格期望有很大偏差，種群細分可能導致顯著偏差。

簡單的疾病例子

觀察到三種隱性疾病表型的攜帶者（雜合子）和受影響個體（純合子）的數量：囊性纖維化（CF）、鐮狀細胞貧血（SC）和β-地中海貧血（βT）。數據改編自Lazarin等人2013年的研究。

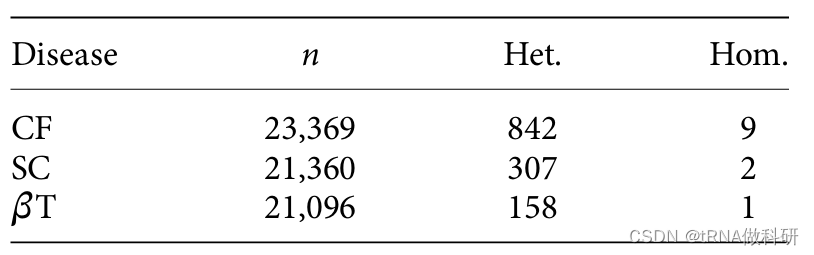
我們首先看看篩查中囊性纖維化（CF）純合子的個體數量：這個數字（9）表明這九個個體總共攜帶了十八個CF等位基因。現在，攜帶者（雜合子）的數量相當多（842），對于一個罕見等位基因來說，這可能是我們預期的情況，因此我們可以計算得到CF等位基因頻率：

 p <- (9+842/2)/23369

得到等位基因頻率約為1.8%

現在，我們有了一個等位基因頻率值（從樣本中估計的種群頻率），它是直接從觀測數據計算出來的。在哈代-溫伯格原理的假設下，我們期望可以用公式2p(1-p)從這個等位基因頻率計算出雜合子的數量。因此，我們預期的攜帶者頻率可以計算為：

2*p*(1-p)

我們得到： 0.03636809

這意味著我們預期大約有3.64%的個體是CF等位基因的攜帶者。?這與實際觀測到的雜合子基因型頻率相比如何？在23,369名接受篩查的人中，共觀察到842名雜合子。即842/23,369，約等于0.03603，或大約3.6%。預期值和觀測值之間的差異非常小。讓我們對鐮狀細胞貧血（SC）和β-地中海貧血（βT）進行相同的計算，我們可以看到2p(1-p)是觀測到的雜合子頻率的一個非常好的預測器。

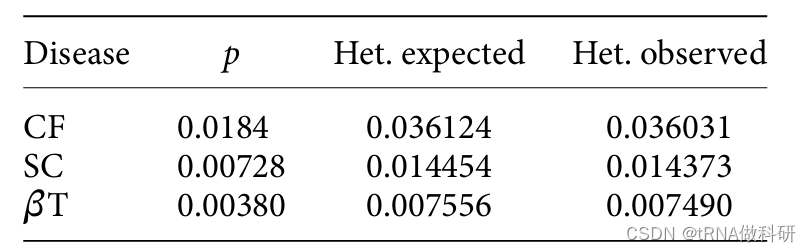
順便說一下，我們還可以看到，對于隱性遺傳疾病，攜帶者的頻率（雜合子）遠高于受影響個體的頻率（純合子）。這符合哈代-溫伯格預測。雜合子與純合子的比例預計為：

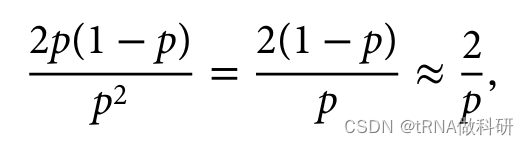
如果說p的值非常小，那么1-p的值就接近為1

從數據庫進行計算

我們使用popgenr數據集，我們首先得安裝，我們使用兩種方式：

如果可以直接下載，則：

install.packages("popgenr")
library("popgenr")

如果下載不成功可以手動安裝，官網下載包，把安裝包放到路徑中
CRAN: Package popgenr (r-project.org)

getwd()
install.packages("popgenr_0.2.tar.gz",repos=NULL)
library("popgenr")

這個snp數據集來自人類基因組的二十五個隨機采樣的等位基因和基因型頻率，現在應該作為對象snp加載。這個snp數據集是從1000 Genomes項目（http://www.internationalgenome.org）中提取的，這是一個全球已知人類遺傳變異的公共庫。

data(snp)
str(snp)

對于分類變量，我們可以進行可視化：

對于R語言的統計知識，可以看我的博客：
【R語言從0到精通】-3-R統計分析（列聯表、獨立性檢驗、相關性檢驗、t檢驗）_r 列聯表分析-CSDN博客

plot(snp$type)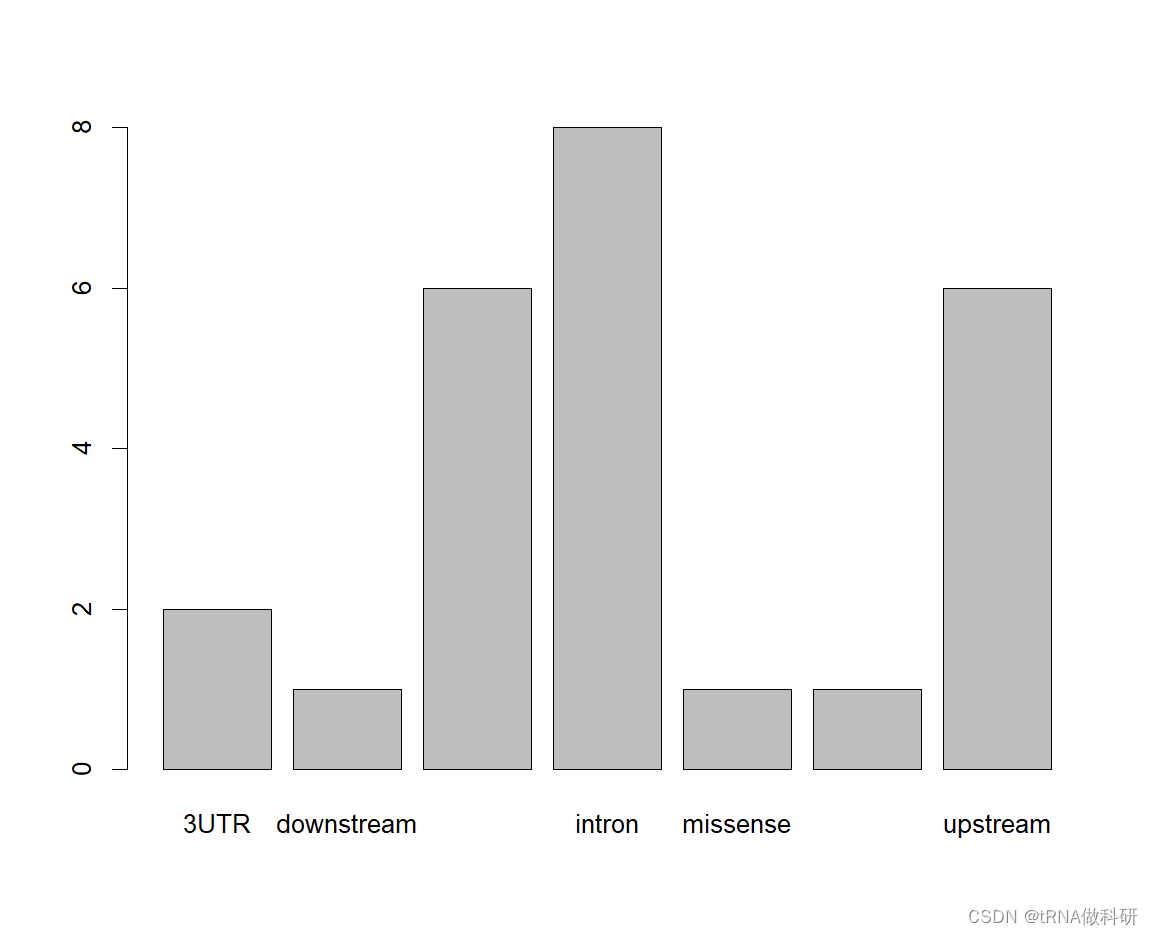

我們還是對于數據進行哈代溫伯格預測與實際對照：

plot(0, 0, type="n", xlim=c(0, 1), ylim=c(0, 1),xlab="Allele frequencies", ylab="Genotype frequencies")
curve(x^2, 0, 1, col="green", lwd=2, add=TRUE)
text(0.6, 0.2, "Homozygotes", col="green")
curve(2*x*(1-x), 0, 1, col="blue", lwd=2, add=TRUE)
text(0.25, 0.5, "Heterozygotes", col="blue")
points(snp$p, snp$hom, pch = 19, col = "green")
points(snp$p, snp$het, pch = 19, col = "blue")

?

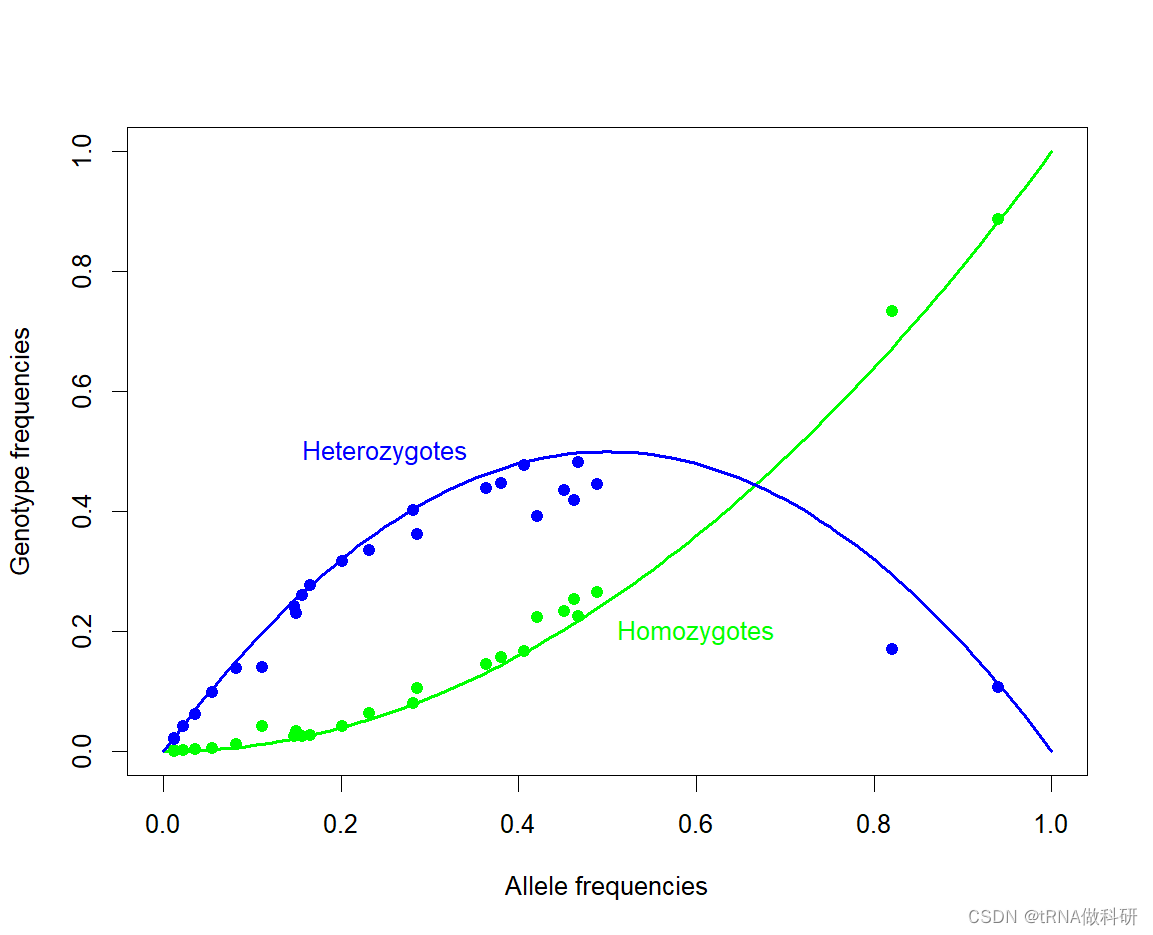總體而言，預測和測量數據之間似乎有很好的一致性。幾個特點顯而易見。與預測的偏差通常表現為雜合性較低，純合性較高。這與人口統計學效應一致，例如不同種群間等位基因頻率的差異，這將在后面更詳細地討論。此外，注意到圖中大多數點的等位基因頻率小于50%；這是因為我們正在繪制的變異是由突變產生的新的等位基因變異（衍生狀態），這些變異來自于預先存在的遺傳序列（通過與人類最近的親屬比較確定的祖先狀態），這些變異往往開始時相當罕見。當我們開始預測等位基因頻率的隨機波動并討論遺傳漂移的概念時，我們將再次回顧這個想法。