二刷力扣——DP算法（子序列問題）

300. 最長遞增子序列

定義是以本元素結尾，所以公式初始化都好弄。但是太慢

class Solution {public int lengthOfLIS(int[] nums) {int n=nums.length;int[] dp = new int[n];//以自己結尾的最長遞增子序列dp[0]=1;int maxzi=1;for(int i=1;i<n;++i){dp[i]=1;for(int j=0;j<i;++j){if(nums[i]>nums[j])dp[i]=Math.max(dp[i],dp[j]+1);} maxzi=Math.max(maxzi,dp[i]);}return maxzi;}
}

時間O（n^2），空間O（n）

看題解的優化：

貪心+二分查找：

下面鏈接說的很清楚：

https://writings.sh/post/longest-increasing-subsequence-revisited

中心思想是：

所以這里的d數組定義是：d[i]是長度為 i 的遞增子序列的最小結尾元素。比如d[2]=6，所以長度為2 的遞增子序列里面，結尾元素最小的情況是2。

所以挨個遍歷nums數組來更新這個d數組，注意這個d數組是動態的，不像之前動態規劃的DP數組，我們得記錄他的長度，因為遇到了nums某元素比d最后的結尾還大，就要把這個某元素加入到d數組，擴大d數組。。如果遇到某元素比結尾小，對應d數組定義，那d數組里面肯定有某個值要更新為這個nums[i]，這個值是哪個位置？就是把比nums[i]大的&最接近nums[i]的換成nums[i]。舉例下圖。遇到3比d 的結尾8要小，所以更新d? 的某個元素，找到比3大的&最接近3 的元素是6，so替換。這樣保證d[2]=3，對應長度為2的遞增子序列的最小結尾元素是3（2、3這個子序列）。

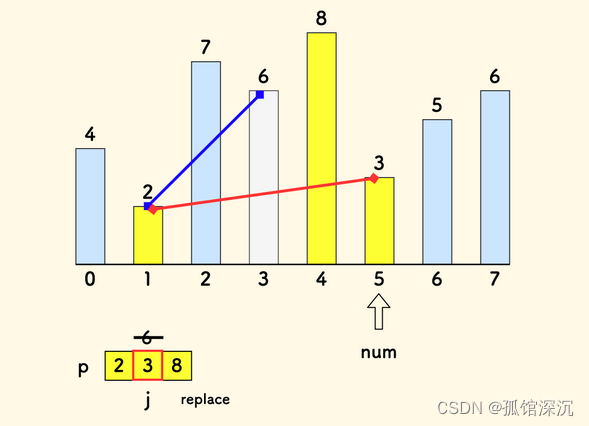
所以在過程中，d數組長度不會減少，所以p數組裝的nums元素的個數，就是所要求的最長遞增子序列長度，d數組的最后結尾元素代表了一條遞增最慢的子序列，所以這個元素的下標，也就是len就是結果。

還有一個解釋：

代碼注意，沒有寫==的時候break，所以退出循環一定是left=right+2了，這個時候left的位置就是比nums[i]大的&最接近nums[i]的位置，然后直接替換成nums[i]。

len是為了記錄包含nums元素的個數，因為這里沒有使用大小可動態變化的集合。

class Solution {public int lengthOfLIS(int[] nums) {int n=nums.length;if(n==0)return 0;int len =1;int[] d = new int[n+1];//長度為i的遞增子序列的最小結尾元素d[len]=nums[0];for(int i=1;i<n;++i){if(nums[i]>d[len])//加到結尾去{d[++len]=nums[i];}else//在d[1]-d[len]中找到更改為nums[i]后使得d仍然有序的位置；二分查找更快{int l=1,r=len;//左閉右閉while(l<=r){int mid=(l+r)>>1;if(d[mid]<nums[i]){l=mid+1;}else r=mid-1;}d[l]=nums[i];//替換}}return len;}
}

貪心遍歷nums，動態規劃遍歷dp，給固定大小的數組的每個元素求解值。

674. 最長連續遞增序列

可以DP數組，也可以貪心省存儲。

貪心：用start記錄連續子序列的開頭下標，發現連續遞增在i 這里斷了，就更新start為i（重新一個遞增序列）。然后取最大值

class Solution {public int findLengthOfLCIS(int[] nums) {int n=nums.length,maxCount=1;int start=0;for(int i=1;i<n;++i){if(nums[i]<=nums[i-1]){start=i;}maxCount=Math.max(maxCount,i-start+1);}return maxCount; }
}

718. 最長重復子數組

dp[i][j]：如果不想單獨初始化的話，dp設置比nums偏移一個坐標，是以nums1[i-1]和nums2[j-1]結尾的子數組最長長度；不偏移的話是nums1[i]和nums2[j]結尾的子數組最長長度

公式：如果遍歷的兩個元素相等，可以在上一個dp[i-1][j-1]的基礎上拼接這個元素，所以+1

偏移：

class Solution {public int findLength(int[] nums1, int[] nums2) {int m=nums1.length,n=nums2.length;int[][] dp=new int[m+1][n+1];//以nums1[i-1]和nums2[j-1]結尾的子數組最長 長度int maxCount=0;for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(nums2[j-1]==nums1[i-1]){dp[i][j]=dp[i-1][j-1]+1;maxCount=Math.max(dp[i][j],maxCount);}}}return maxCount;}
}

還可以用滾動數組實現，注意跟 01背包的滾動數組實現一樣，留下的那個維度只能在內循環，而且得從大到小，因為得是上一輪的值而不是這一輪更新過的值。

而且不相等的時候，要把dp[j]清零，因為二維的時候不操作dp[i][[j]直接就是0；但是一維的時候不操作是繼承了上一輪的值，是錯的。只要不相等以nums1[i-1]結尾的子數組長度就是0，所以置零。

class Solution {public int findLength(int[] nums1, int[] nums2) {int m=nums1.length,n=nums2.length;int[] dp=new int[m+1];//以nums1[i-1] 結尾的子數組最長 長度int maxCount=0;for(int i=1;i<=n;++i){for(int j=m;j>=1;--j)//留下維度從大到小{if(nums2[i-1]==nums1[j-1]){dp[j]=dp[j-1]+1;maxCount=Math.max(dp[j],maxCount);}else dp[j]=0;   //不相等了，清零}}return maxCount;}
}

不偏移：

class Solution {public int findLength(int[] nums1, int[] nums2) {int m=nums1.length,n=nums2.length;int[][] dp=new int[m ][n ];//nums1[i]和nums2[j]結尾的子數組最長 長度int maxCount=0;for(int i=0;i<n;++i){dp[0][i]=nums1[0]==nums2[i]?1:0;maxCount=Math.max(dp[0][i],maxCount);}for(int i=0;i<m;++i){dp[i][0]=nums1[i]==nums2[0]?1:0;maxCount=Math.max(dp[i][0],maxCount);}for(int i=1;i<m;++i){for(int j=1;j<n;++j){if(nums2[j]==nums1[i]){dp[i][j]=dp[i-1][j-1]+1;maxCount=Math.max(dp[i][j],maxCount);}}}return maxCount;}
}

1143. 最長公共子序列

dp[i][j]的定義跟上面不一樣，這里子序列是不連續的，如果定義還要求是以元素結尾的子序列長度的話，i元素=j元素，dp[i][j]不一定是在dp[i-1][j-1]的基礎上+1，就會很麻煩。

所以設置為：text1[0,i-1]和text2[0,j-1]范圍內，最長公共子序列的長度.

最后返回的就是dp[m][n]

遞推公式：如果相等的話，是在dp[i-1][j-1]的基礎上+1。

如果不相等，不能直接跳過，比如abcde，ace，到了abc、ace的時候c!=e，那么dp[3][3]按照定義應該是2，等于dp[3][2]。把abc、ace倒過來，dp[3][3]又=dp[2][3]。A[i-1]和B[j-1]不相等，但是A[i-1]可能和B[j-1]之前的相等，B[j-1]可能和A[i-1]之前的相等，所以要取這兩種情況的最大值。

采用跟上提一樣的偏移寫法：

class Solution {public int longestCommonSubsequence(String text1, String text2) {int m=text1.length(),n=text2.length();int[][] dp=new int[m+1][n+1];//text1[0,i-1]和text2[0,j-1]范圍內，最長公共子序列的長度for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(text1.charAt(i-1)==text2.charAt(j-1)){dp[i][j]=dp[i-1][j-1]+1;}else dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);}}return dp[m][n];}
}

同樣可以用滾動數組嗎？

不行，

dp[i][j]取決于這三個元素，如果用滾動數組，無論行優先，還是列優先遍歷，dp[i][j-1]/dp[i-1][j]都會把dp[i][j]覆蓋。

1035. 不相交的線

跟上題一樣。

392. 判斷子序列

編輯距離問題的入門題目。用上面的方法然后判斷dp[m][n]是否=s.length()的話，效率低。

所以也可以用雙指針做一下：

class Solution {public boolean isSubsequence(String s, String t) {int m=s.length(),n=t.length();int sp=0,tp=0;while(sp<m && tp<n)//sp:s已經匹配了的右邊界{if(s.charAt(sp)==t.charAt(tp)){sp++;}tp++;}if(sp==m)return true;return false;}
}

時間O(n)。

有一個進階問題；

力扣題解給出一個跟S 無關的預處理DP數組的做法：dp[i][j] 表示字符串 t 中從位置 i 開始往后字符 j 第一次出現的位置。

遞推公式：

初始化：有效的下標 i 就是0到n-1，所以多設置一個n ，讓dp[n][j]都=n，代表位置不存在。這是判斷false的條件。

遍歷順序：得到下標 i到n-1 的第一次位置，所以i 需要從大到小。

class Solution {public boolean isSubsequence(String s, String t) {int m=s.length(),n=t.length();int[][] dp=new int[n+1][26];//字符串 t 中從位置 i 開始往后字符 j 第一次出現的位置//初始化for(int i=0;i<26;++i){dp[n][i]=n;//代表不存在}for(int i=n-1;i>=0;--i)//和s無關，得到dp數組{for(int j=0;j<26;++j){if(t.charAt(i)==j+'a'){dp[i][j]=i;//更新位置}else dp[i][j]=dp[i+1][j];}}//檢查S1、S2……int add=-1;for(int i=0;i<m;++i){add=dp[add+1][s.charAt(i)-'a'];//以上一次找到的位置的下一個為起點System.out.println(add);if(add==n)return false;}return true;}
}

過程大概就是：

s = "abc", t = "ahbgdc"

s[0]=a在t[0,n-1]的第一個位置，是0；

s[1]=b在t[1,n-1]的第一個位置，是2；

s[2]=c在t[3,n-1]的第一個位置，是5；

保證了s各字母在t中找到的位置是遞增的，而且這個位置不等于代表不存在的n，就返回true。

115. 不同的子序列

仔細看題目，在s 的 子序列 中 t 出現的個數。s的子序列是不連續的，t是整個連續的。

定義dp的時候，dp[i][j]表示在s[0-i]（不一定以i結尾）中t[0,j]（連續，一定以j結尾）出現的個數。

所以這里dp[i][j]有兩種可能：以s[i]結尾和不以s[i]結尾，這是分情況討論的來源。

1、當s[i-1]==t[j-1]，以s[i-1]結尾的話，t[j-1]也定了，所以只能等于不包含這兩個相同元素的個數，也就是dp[i-1][j-1]；

不以s[i-1]結尾的話，那就是不包含這個元素，所以要找這個元素之前子序列出現個數，即dp[i-1][j]。

遞推公式題解中的解釋，力扣給的逆序的DP：

2、當s[i-1]!=t[j-1]，肯定只會是不以s[i-1]結尾了，所以讓s[0,i-2]和t[0,j-1]匹配，即dp[i-1][j]。

初始化：如果像上面的那樣，初始化為0，結果只會是0。先看dp[i][0]，s[0-i-1]包含空串的數量，應該為1；而且空串也是空串的子串，所以dp[0][0]=1。dp[0][j]，空串包含t[0,j-1]的數量，應該是0。

class Solution {public int numDistinct(String s, String t) {int m=s.length(),n=t.length();int[][] dp=new int[m+1][n+1];//在s[0-i-1]（不要求以i結尾）的子序列中t[0,j-1]（要以j結尾）出現的個數for(int i=0;i<=m;++i)dp[i][0]=1;for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(s.charAt(i-1)==t.charAt(j-1))dp[i][j]=dp[i-1][j ]+dp[i-1][j-1];else dp[i][j]=dp[i-1][j];}}return dp[m][n];}
}

用Java不用取余也能過。

也可以用滾動數組。注意內循環也得從大到小：

class Solution {public int numDistinct(String s, String t) {int m=s.length(),n=t.length();int[] dp=new int[n+1];//在s[0-i-1]（不要求以i結尾）的子序列中t[0,j-1]（要以j結尾）出現的個數dp[0]=1;for(int i=1;i<=m;++i){for(int j=n;j>=1;--j)//避免覆蓋上一輪的{if(s.charAt(i-1)==t.charAt(j-1))dp[j]+=dp[j-1];// else dp[j]=dp[j];}}return dp[n];}
}

583. 兩個字符串的刪除操作

dp[i][j]定義：1[0—i]、2[0—j ]相等的最小步數。

初始化：根據定義，dp[0][i]應該=i；同理dp[0][j]=j。

2元素相等，那肯定這一步不用刪除元素，直接等于之前的dp[i-1][j-1]

2個元素不相等的時候，需要刪除，那就有三種情況。刪一個有兩種，或者兩個都刪。既然是最小步數，所以取最小值。

class Solution {public int minDistance(String word1, String word2) {int m=word1.length(),n=word2.length();int[][] dp=new int[m+1][n+1];//1[0,i-1]、2[0,j-1]相等的最小步數for (int i = 1; i <= m; i++)dp[i][0] = i;for (int j = 1; j <= n; j++)dp[0][j] = j;for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(word1.charAt(i-1)==word2.charAt(j-1)){dp[i][j]=dp[i-1][j-1];}else dp[i][j]=Math.min(Math.min(dp[i-1][j],dp[i][j-1])+1,dp[i-1][j-1]+2);}}return dp[m][n];}
}

也不能滾動數組。

最后，綜合題：

72. 編輯距離

相等和上面是一樣的。

不相等:（注意只能操作word1）

增：dp[i][j-1]+1。增了之后新增的和2[j-1]相等。

刪：dp[i-1][j]+1

換：dp[i-1][j-1]+1

關于增刪情況的解釋：

所以取這三個的最小值。

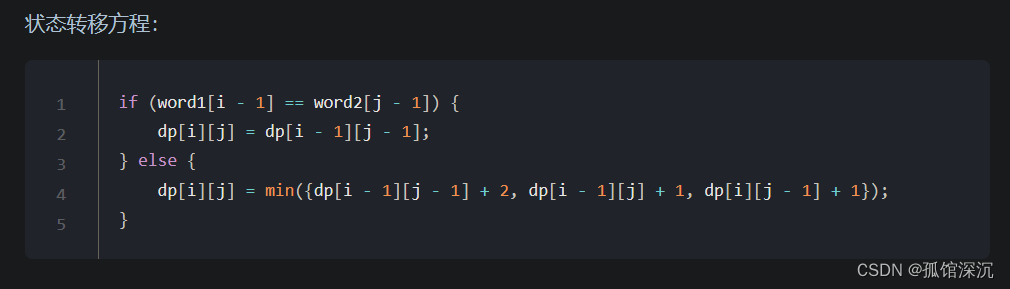
class Solution {public int minDistance(String word1, String word2) {int m=word1.length(),n=word2.length();int[][] dp=new int[m+1][n+1];//1[0,i-1]轉化成2[0,j-1]for(int i=1;i<=m;++i)dp[i][0]=i;for(int j=1;j<=n;++j)dp[0][j]=j;for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(word1.charAt(i-1)==word2.charAt(j-1)){dp[i][j]=dp[i-1][j-1];}else {dp[i][j]=1+Math.min(dp[i-1][j-1],Math.min(dp[i][j-1],dp[i-1][j]));}}}return dp[m][n];}
}