由初中的幾何知識我們可以知道，確定一個三角形至少需要三個不共線的點，因此確定一個三角形的外接圓至少可用三個點。我們不妨假設三個點坐標為P1(x1,y1,z1),P2(x2,y2,z2),P3(x3,y3,z3)。
圓方程的標準形式為：
(xi-x)2+(yi-y)2=R2 （1）
在三維空間坐標系中球的方程為：
(xi-x)2+(yi-y)2+(zi-z)2=R2 （2）
一個空間圓的產生可以看作過該圓心的一個球體，被一個經過該點的平面所截而得到。因此在求取空間圓的時候還應添加平面約束方程，以上述P1、P2、P3三個不共線的點可以確定一個平面，平面方程為：
AX+BY+CZ+D=0 (3)
求解方程(3)時注意技巧，常用兩種方式，向量法或者待定系數法。若使用待定系數法則需平面方程的另一種形式,點法式為：
A(x-x0)+B(y-y0)+C(z-z0)=0 (4)
但是筆者建議使用向量的方式，更為簡單方便，三點在同一個平面上，以P1為基點，尋找兩條向量P12、P13；該平面方程的法向量為n=P12×P13（注:向量的叉乘）。在得到平面的法向量之后，帶入其中一個點到方程(4)中即可得到平面約束方程。我們不妨將該約束方程系數設為A1、B1、C1、D1。
在得到約束平面方程之后還須求解空間中圓的方程，在求解圓的方程時也有諸多方式，一種方式為將已知點帶入到方程(2)中，利用待定系數法求解,我們仍參以P1為方程的基點，分別將P2,P3帶入可以得到如下方程：
(x1-x)2+(y1-y)2+(z1-z)2=R2
(x2-x)2+(y2-y)2+(z2-z)2=R2
(x3-x)2+(y3-y)2+(z3-z)2=R2
整理后可以得到
A2=2(x2-x1) ,B2=2(y2-y1) ,C2=2(z2-z1),D2=-(x12+y12+z12-x22-y22-z22) (5)
A3=2(x3-x1) ,B3=2(y3-y1) ,C3=2(z3-z1),D3=-(x12+y12+z12-x32-y32-z32) (6)
建立系數矩陣:

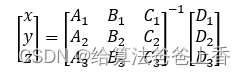
求解上述方程即可得到空間圓心坐標(x,y,z)。

RANSAC空間圓擬合的代碼實現如下：

#include <iostream>
#include <pcl/io/pcd_io.h>
#include <pcl/point_types.h>
#include <pcl/common/distances.h>int main()
{pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);pcl::io::loadPCDFile("circle_3D.pcd", *cloud);int iters = 100;					//迭代次數float F_thre = 0.1, D_thre = 0.1;	//點到空間圓所在平面的距離閾值，半徑誤差閾值int max_inner_count = 0;			//最大內點個數pcl::PointXYZ O;					//圓心float R;							//半徑srand(time(0));						//隨機數種子for (size_t i = 0; i < iters; i++)	//循環迭代{int n1 = rand() % cloud->size(), n2 = rand() % cloud->size(), n3 = rand() % cloud->size();pcl::PointXYZ p1 = cloud->points[n1], p2 = cloud->points[n2], p3 = cloud->points[n3];	//從點云隨機取三個點float A1 = (p2.y - p1.y) * (p3.z - p1.z) - (p2.z - p1.z) * (p3.y - p1.y);	//計算空間圓所在平面方程float B1 = (p2.z - p1.z) * (p3.x - p1.x) - (p2.x - p1.x) * (p3.z - p1.z);float C1 = (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x);float D1 = -(A1 * p1.x + B1 * p1.y + C1 * p1.z);float A2 = 2 * (p2.x - p1.x);float B2 = 2 * (p2.y - p1.y);float C2 = 2 * (p2.z - p1.z);float D2 = p1.x * p1.x + p1.y * p1.y + p1.z * p1.z - p2.x * p2.x - p2.y * p2.y - p2.z * p2.z;float A3 = 2 * (p3.x - p1.x);float B3 = 2 * (p3.y - p1.y);float C3 = 2 * (p3.z - p1.z);float D3 = p1.x * p1.x + p1.y * p1.y + p1.z * p1.z - p3.x * p3.x - p3.y * p3.y - p3.z * p3.z;Eigen::Matrix3f A;A << A1, B1, C1, A2, B2, C2, A3, B3, C3;Eigen::Vector3f D;D << -D1, -D2, -D3;auto X = A.inverse() * D;pcl::PointXYZ p(X[0], X[1], X[2]);float r = (pcl::euclideanDistance(p, p1) + pcl::euclideanDistance(p, p2) + pcl::euclideanDistance(p, p3)) / 3;//std::cout << r << std::endl;int inner_count = 0;for (size_t i = 0; i < cloud->size(); i++){float Fi = abs(A1 * cloud->points[i].x + B1 * cloud->points[i].y + C1 * cloud->points[i].z + D1) / sqrt(A1 * A1 + B1 * B1 + C1 * C1);	//點到平面距離float Di = abs(pcl::euclideanDistance(p, cloud->points[i]) - r);																		//點到圓心距離于半徑差值if (Fi < F_thre && Di < D_thre)inner_count++;}if (inner_count > max_inner_count)	//如果本輪迭代內點個數更多，則更新圓心和半徑{max_inner_count = inner_count;O = p;R = r;}}std::cout << O << " " << R << std::endl;return 0;
}

參考：在空間三維坐標系下的圓、直線和平面擬合