1. Lipschitz 連續
經常聽到這個名詞, Lipschitz 連續比普通連續更強,不僅要求函數連續,還要求函數的梯度小于一個正實數。
在單變量實數函數上的定義可以是:
- 對于定義域內任意兩個 x 1 x_1 x1? and x 2 x_2 x2?, 存在一個 K > 0 K>0 K>0, 滿足
∣ f ( x 1 ) ? f ( x 2 ) ∣ ≤ K ∣ ( x 1 ? x 2 ) ∣ |f(x_1)-f(x_2)|\leq K|(x_1-x_2)| ∣f(x1?)?f(x2?)∣≤K∣(x1??x2?)∣
對于多變量函數,要求在任何一個變量上的梯度都小于等于 K K K.
2. 絕對連續
除了 Lipschitz 連續,還有絕對連續(absolute continuous, 不僅要求一致連續,還要求函數勒貝格可積分),一致連續以及普通連續,這幾個連續在集合上的包含關系是:
Lipschitz?continuous ? absolute?continuous ? uniform?continuous ? ordinary?continuous \text{Lipschitz continuous}\subset\text{absolute continuous}\subset\text{uniform continuous}\subset\text{ordinary continuous} Lipschitz?continuous?absolute?continuous?uniform?continuous?ordinary?continuous
絕對連續的定義:
- 對于任意實數 ? > 0 \epsilon>0 ?>0 與定義域內任意不相交的子區間序列 ( x k , y k ) (x_k,y_k) (xk?,yk?),總存在實數 δ > 0 \delta>0 δ>0,當 ∑ k ∣ x ? y ∣ < δ \sum _k|x-y|<\delta ∑k?∣x?y∣<δ 時,都有 ∑ k ∣ f ( x ) ? f ( y ) ∣ < ? \sum _k |f(x)-f(y)|<\epsilon ∑k?∣f(x)?f(y)∣<?.
一致連續但不是絕對連續的一個函數: x / sin ? ( 1 / x ) x/\sin(1/x) x/sin(1/x),它的圖像是:
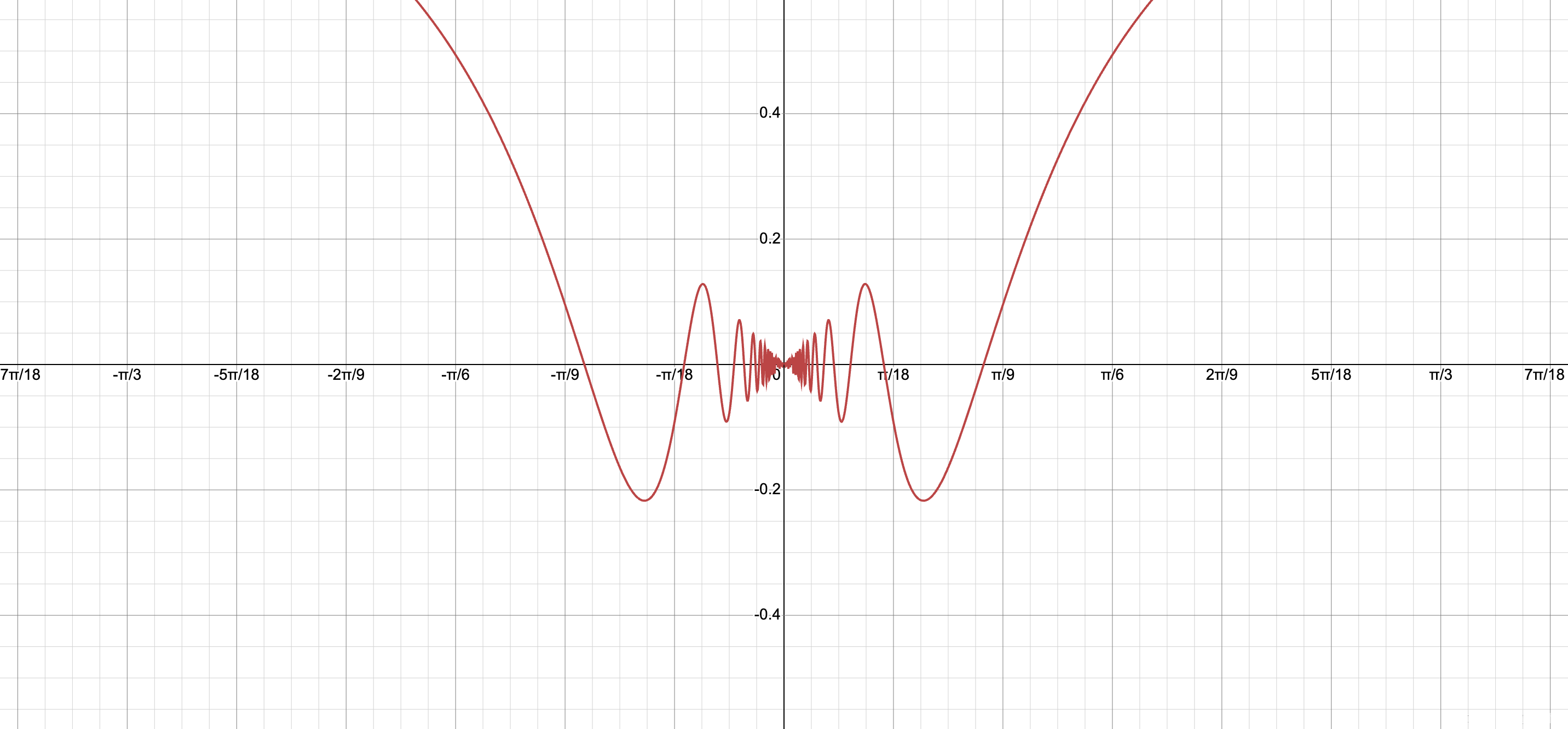
這個函數可以在定義域內找到不相交的子區間,它們的長度和小于某個常數,但是在所有子區間的絕對偏差和可以達到無窮大 (令 x n = 1 2 n π + π / 2 , y n = 1 2 n π , n ≥ 1 x_n=\frac{1}{2n\pi+\pi/2}, y_n=\frac{1}{2n\pi}, n\geq 1 xn?=2nπ+π/21?,yn?=2nπ1?,n≥1)。
該函也不是勒貝格可積,因為:
∫ ? ∞ ∞ ∣ x sin ? ( 1 / x ) ∣ = ∞ \int_{-\infty}^{\infty}\left|\frac{x}{\sin(1/x)}\right|=\infty ∫?∞∞? ?sin(1/x)x? ?=∞
(對函數的絕對值求積分,不是無窮大,是存在勒貝格積分的條件)

)

)













)

