C++算法學習心得八.動態規劃算法（6）

1.最長遞增子序列（300題）

題目描述：

給你一個整數數組 nums ，找到其中最長嚴格遞增子序列的長度。

子序列是由數組派生而來的序列，刪除（或不刪除）數組中的元素而不改變其余元素的順序。例如，[3,6,2,7] 是數組 [0,3,1,6,2,2,7] 的子序列。

示例 1：

輸入：nums = [10,9,2,5,3,7,101,18]
輸出：4
解釋：最長遞增子序列是 [2,3,7,101]，因此長度為 4 。

?dp[i]表示i之前包括i的以nums[i]結尾的最長遞增子序列的長度

if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

注意這里不是要dp[i] 與 dp[j] + 1進行比較，而是我們要取dp[j] + 1的最大值。

每一個i，對應的dp[i]（即最長遞增子序列）起始大小至少都是1.

dp[i] 是有0到i-1各個位置的最長遞增子序列推導而來，那么遍歷i一定是從前向后遍歷

j其實就是遍歷0到i-1，那么是從前到后，還是從后到前遍歷都無所謂，只要吧 0 到 i-1 的元素都遍歷了就行了。所以默認習慣從前向后遍歷。

class Solution {
public:int lengthOfLIS(vector<int>& nums) {if(nums.size() <= 1)return nums.size();vector<int>dp(nums.size(),1);int result = 0;for(int i = 1;i < nums.size();i++){for(int j = 0;j < i;j++){if(nums[j] < nums[i])dp[i] = max(dp[i],dp[j] + 1);}if(dp[i] > result)result = dp[i];}return result;}
};

時間復雜度: O(n^2)
空間復雜度: O(n)

2.最長連續遞增序列(674題）

題目描述：

給定一個未經排序的整數數組，找到最長且連續遞增的子序列，并返回該序列的長度。

連續遞增的子序列可以由兩個下標 l 和 r（l < r）確定，如果對于每個 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是連續遞增子序列。

示例 1：

輸入：nums = [1,3,5,4,7]
輸出：3
解釋：最長連續遞增序列是 [1,3,5], 長度為3。盡管 [1,3,5,7] 也是升序的子序列, 但它不是連續的，因為 5 和 7 在原數組里被 4 隔開。

dp[i]：以下標i為結尾的連續遞增的子序列長度為dp[i],

如果 nums[i] > nums[i - 1]，那么以 i 為結尾的連續遞增的子序列長度一定等于以i - 1為結尾的連續遞增的子序列長度 + 1 。

即：dp[i] = dp[i - 1] + 1;

因為本題要求連續遞增子序列，所以就只要比較nums[i]與nums[i - 1]，而不用去比較nums[j]與nums[i] （j是在0到i之間遍歷）。

既然不用j了，那么也不用兩層for循環，本題一層for循環就行，比較nums[i] 和 nums[i - 1]。

以下標i為結尾的連續遞增的子序列長度最少也應該是1，即就是nums[i]這一個元素。

所以dp[i]應該初始1;

?dp[i + 1]依賴dp[i]，所以一定是從前向后遍歷。

class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {if(nums.size() == 0)return nums.size();vector<int>dp(nums.size(),1);int result = 1;for(int i = 1;i < nums.size();i++){if(nums[i] > nums[i - 1])dp[i] = dp[i - 1] + 1;if(dp[i] > result)result = dp[i];}return result;}
};

時間復雜度：O(n)
空間復雜度：O(n)

貪心算法:

遇到nums[i] > nums[i - 1]的情況，count就++，否則count為1，記錄count的最大值就可以了。

class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {if(nums.size() == 0)return nums.size();int result = 1;int count = 1;for(int i = 1;i < nums.size();i++){if(nums[i] > nums[i - 1]){count++;}else{count = 1;}if(count > result)result = count;}return result;}
};

時間復雜度：O(n)
空間復雜度：O(1)

3.最長重復子數組(718題）

題目描述：

給兩個整數數組?A?和?B?，返回兩個數組中公共的、長度最長的子數組的長度。

示例：

輸入：

A: [1,2,3,2,1]
B: [3,2,1,4,7]
輸出：3
解釋：長度最長的公共子數組是 [3, 2, 1] 。

?dp[i][j] ：以下標i - 1為結尾的A，和以下標j - 1為結尾的B，最長重復子數組長度為dp[i][j]。（特別注意： “以下標i - 1為結尾的A” 標明一定是以A[i-1]為結尾的字符串）

dp[i][j]的定義，dp[i][j]的狀態只能由dp[i - 1][j - 1]推導出來。

即當A[i - 1] 和B[j - 1]相等的時候，dp[i][j] = dp[i - 1][j - 1] + 1;

dp[i][0] 和dp[0][j]初始化為0

外層for循環遍歷A，內層for循環遍歷B。

class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>>dp(nums1.size() + 1,vector<int>(nums2.size() + 1,0));int result = 0;for(int i = 1;i <= nums1.size();i++){for(int j = 1;j <= nums2.size();j++){if(nums1[i - 1] == nums2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;if(dp[i][j] > result)result = dp[i][j];}}return result;}
};

時間復雜度：O(n × m)，n 為A長度，m為B長度
空間復雜度：O(n × m)

?4.最長公共子序列(1143題）

題目描述：

給定兩個字符串?text1 和?text2，返回這兩個字符串的最長公共子序列的長度。

一個字符串的?子序列?是指這樣一個新的字符串：它是由原字符串在不改變字符的相對順序的情況下刪除某些字符（也可以不刪除任何字符）后組成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。兩個字符串的「公共子序列」是這兩個字符串所共同擁有的子序列。

若這兩個字符串沒有公共子序列，則返回 0。

示例 1:

輸入：text1 = "abcde", text2 = "ace"
輸出：3
解釋：最長公共子序列是 "ace"，它的長度為 3。

dp[i][j]：長度為[0, i - 1]的字符串text1與長度為[0, j - 1]的字符串text2的最長公共子序列為dp[i][j]

text1[i - 1] 與 text2[j - 1]相同，text1[i - 1] 與 text2[j - 1]不相同

如果text1[i - 1] 與 text2[j - 1]相同，那么找到了一個公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 與 text2[j - 1]不相同，那就看看text1[0, i - 2]與text2[0, j - 1]的最長公共子序列和 text1[0, i - 1]與text2[0, j - 2]的最長公共子序列，取最大的。

即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

dp[i][0] = 0;

同理dp[0][j]也是0。

從前向后，從上到下來遍歷這個矩陣。

dp[text1.size()][text2.size()]為最終結果

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>>dp(text1.size()+1,vector<int>(text2.size()+1,0));for(int i = 1;i <= text1.size();i++){for(int j = 1;j <= text2.size();j++){if(text1[i - 1] == text2[j - 1]){dp[i][j] = dp[i - 1][j - 1] + 1;}else{dp[i][j] = max(dp[i - 1][j],dp[i][j - 1]);}}}return dp[text1.size()][text2.size()];}
};

時間復雜度: O(n * m)，其中 n 和 m 分別為 text1 和 text2 的長度
空間復雜度: O(n * m)

?5.不相交的線(1035題）

題目描述：

在兩條獨立的水平線上按給定的順序寫下?nums1?和?nums2?中的整數。

現在，可以繪制一些連接兩個數字?nums1[i]?和?nums2[j]?的直線，這些直線需要同時滿足滿足：

?nums1[i] == nums2[j]
且繪制的直線不與任何其他連線（非水平線）相交。

請注意，連線即使在端點也不能相交：每個數字只能屬于一條連線。

以這種方法繪制線條，并返回可以繪制的最大連線數。

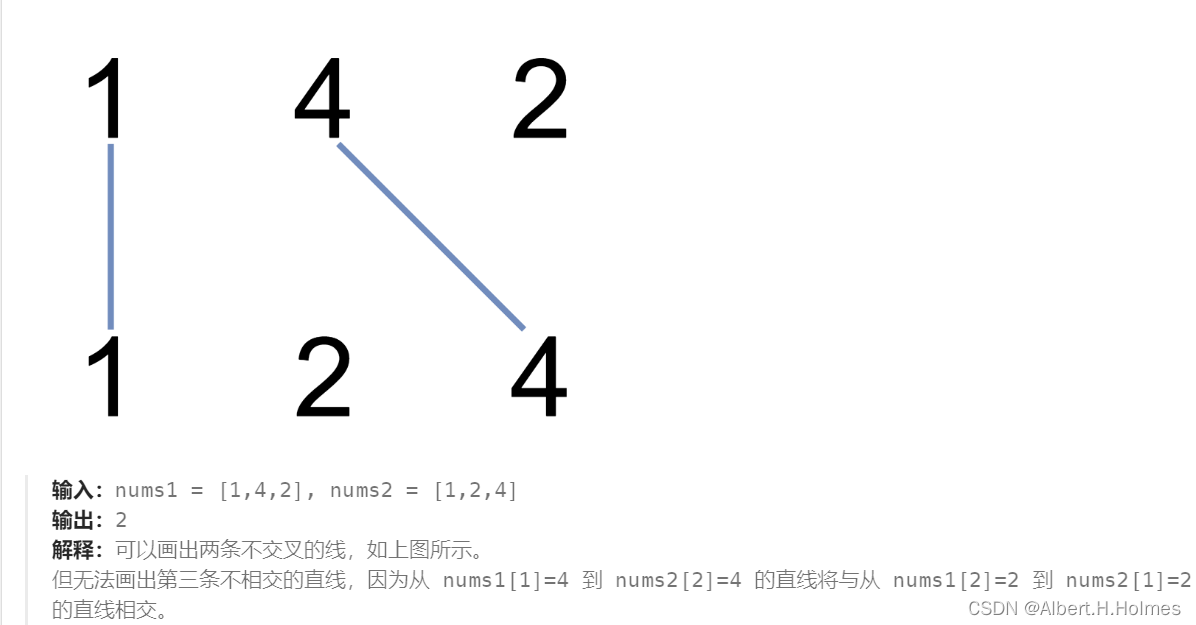
本題說是求繪制的最大連線數，其實就是求兩個字符串的最長公共子序列的長度?

class Solution {
public:int maxUncrossedLines(vector<int>& A, vector<int>& B) {vector<vector<int>> dp(A.size() + 1, vector<int>(B.size() + 1, 0));for (int i = 1; i <= A.size(); i++) {for (int j = 1; j <= B.size(); j++) {if (A[i - 1] == B[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[A.size()][B.size()];}
};

時間復雜度: O(n * m)
空間復雜度: O(n * m)

6.?最大子序和（53題）

題目描述：

給定一個整數數組 nums?，找到一個具有最大和的連續子數組（子數組最少包含一個元素），返回其最大和。

示例:

輸入: [-2,1,-3,4,-1,2,1,-5,4]
輸出: 6
解釋:?連續子數組?[4,-1,2,1] 的和最大，為?6。

?dp[i]：包括下標i（以nums[i]為結尾）的最大連續子序列和為dp[i]。

dp[i]只有兩個方向可以推出來：

dp[i - 1] + nums[i]，即：nums[i]加入當前連續子序列和
nums[i]，即：從頭開始計算當前連續子序列和

一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

遞推公式可以看出來dp[i]是依賴于dp[i - 1]的狀態，dp[0]就是遞推公式的基礎。

dp[0]應該是多少呢?

根據dp[i]的定義，很明顯dp[0]應為nums[0]即dp[0] = nums[0]。

遞推公式中dp[i]依賴于dp[i - 1]的狀態，需要從前向后遍歷，在遞推公式的時候，可以直接選出最大的dp[i]

class Solution {
public:int maxSubArray(vector<int>& nums) {if(nums.size() == 0)return 0;vector<int>dp(nums.size(),0);//dp[i]表示包括i之前的最大連續子序列和dp[0] = nums[0];int result = dp[0];for(int i = 1;i < nums.size();i++){dp[i] = max(dp[i-1]+nums[i],nums[i]);//狀態轉移公式，舍棄前面和當前基礎上再繼續加和if(dp[i] > result)result = dp[i];//result 保存dp[i]的最大值}return result;}
};

時間復雜度：O(n)
空間復雜度：O(n)

總結：

?最長遞增子序列：給定一個序列，其內部順序是不定的，所以這里要求最大升序序列長度，那么先定義dp數組的含義dp[i]代表i之前包括i的以nums[i]結尾的最長遞增子序列的長度，進行初始化操作，dp[i]大小為數組大小，且都賦值1，因為設定是長度至少有1，遍歷順序需要雙循環來外層I是從1到nums.size()，內層循環從0到i進行遍歷，遞推公式：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);還要記得需要更新dp[i]的值if(dp[i] > result)result = dp[i];最后返回result即可

最長連續遞增序列：動態規劃：上一題基礎上，介紹dp[i]：以下標i為結尾的連續遞增的子序列長度為dp[i],如果 nums[i] > nums[i - 1]，那么以 i 為結尾的連續遞增的子序列長度一定等于以i - 1為結尾的連續遞增的子序列長度 + 1。遞推公式：dp[i] = dp[i - 1] + 1，本題要求連續遞增子序列，所以就只要比較nums[i]與nums[i - 1]，而不用去比較nums[j]與nums[i] （j是在0到i之間遍歷），貪心算法：遇到nums[i] > nums[i - 1]的情況，count就++，否則count為1，記錄count的最大值就可以了。

最長重復子數組：給定兩個數組，然后對這兩個數組求最大重復子數組，dp[i][j] ：以下標i - 1為結尾的A，和以下標j - 1為結尾的B，最長重復子數組長度為dp[i][j]，dp[i][j]的定義，dp[i][j]的狀態只能由dp[i - 1][j - 1]推導出來，遞推公式：A[i - 1] 和B[j - 1]相等的時候，dp[i][j] = dp[i - 1][j - 1] + 1，初始化：dp[i][0] 和dp[0][j]初始化為0，遍歷順序：外層for循環遍歷A，內層for循環遍歷B。

最長公共子序列：給定兩個字符串，但是呢需要求的子序列是不改變相對順序，且可以刪除字符，dp[i][j]：長度為[0, i - 1]的字符串text1與長度為[0, j - 1]的字符串text2的最長公共子序列為dp[i][j]，text1[i - 1] 與 text2[j - 1]相同，text1[i - 1] 與 text2[j - 1]不相同，如果text1[i - 1] 與 text2[j - 1]相同，那么找到了一個公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;如果text1[i - 1] 與 text2[j - 1]不相同，那就看看text1[0, i - 2]與text2[0, j - 1]的最長公共子序列和 text1[0, i - 1]與text2[0, j - 2]的最長公共子序列，取最大的。即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

不相交的線：求繪制的最大連線數，其實就是求兩個字符串的最長公共子序列的長度?，整體代碼和上一個最長公共子序列流程一樣，想法也大致相同，只是換一些字母。

最大子序和：dp[i]：包括下標i（以nums[i]為結尾）的最大連續子序列和為dp[i]，dp[i]只有兩個方向，一個是dp[i-1]+nums[i]，還有從開始nums[i]開始，遞推公式：dp[i] = max(dp[i - 1] + nums[i], nums[i])，dp[0]應為nums[0]即dp[0] = nums[0]，dp[i]依賴于dp[i - 1]的狀態，需要從前向后遍歷，在遞推公式的時候，可以直接選出最大的dp[i]。