說明
- 導數
- 偏微分
- 梯度
梯度:是一個向量,向量的每一個軸是每一個方向上的偏微分
梯度是有方向也有大小,梯度的方向代表函數在當前點的一個增長的方向,然后這個向量的長度代表了這個點增長的速率

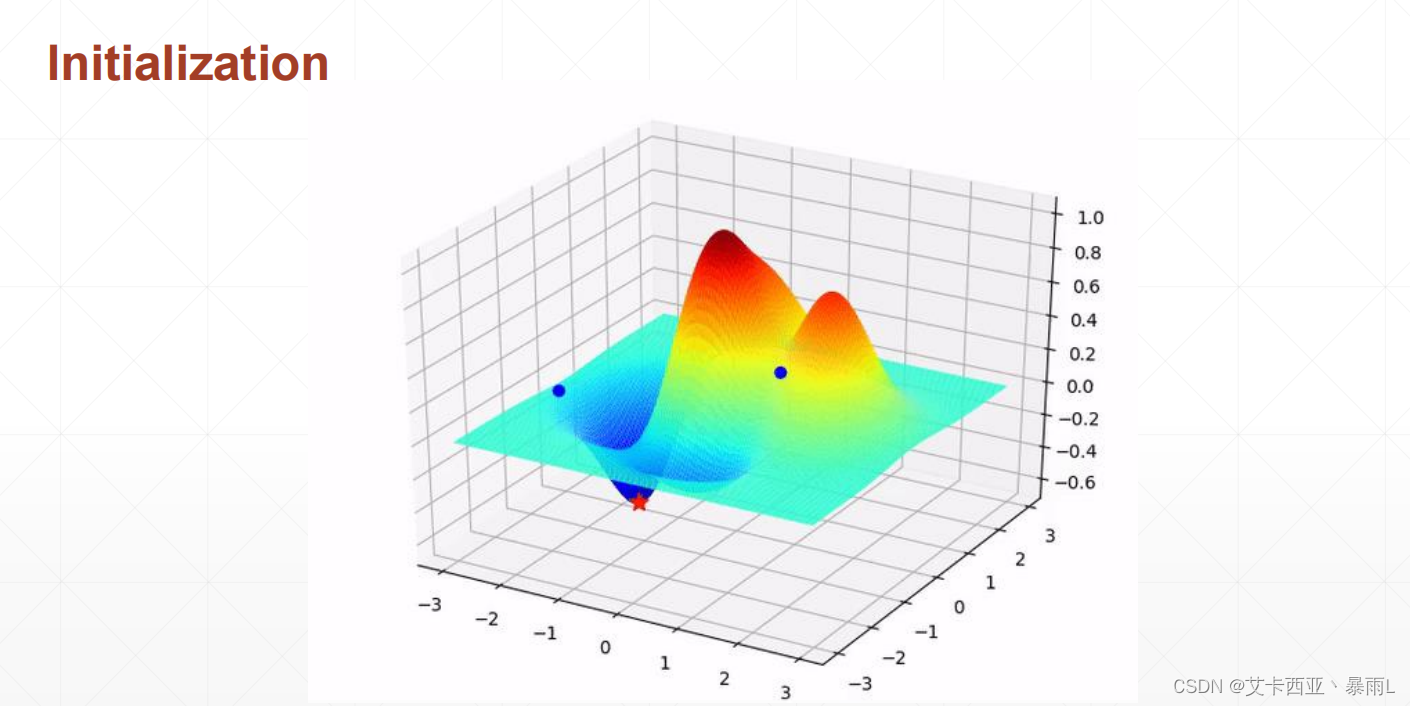
藍色代表比較小的值,紅色代表比較大的值,中間的箭頭比較長,方向是由一個極小值指向一個極大值,因此中間這部分梯度反應了函數的增長的方向,說明了從這個方向增長這個方向是最快的
如何搜索到一個極小值?
一般情況下我們搜索的是極小值,如果想要搜索極大值的話,可以把loss變成負號,就可以通過搜索一個極小值解來搜索極大值解

所以這個函數的梯度是(2 θ 1 \theta_{1} θ1?,2 θ 2 \theta_{2} θ2?),再求(0,0)處的一個梯度情況,因此有時候會陷入到一個局部最小值的情況
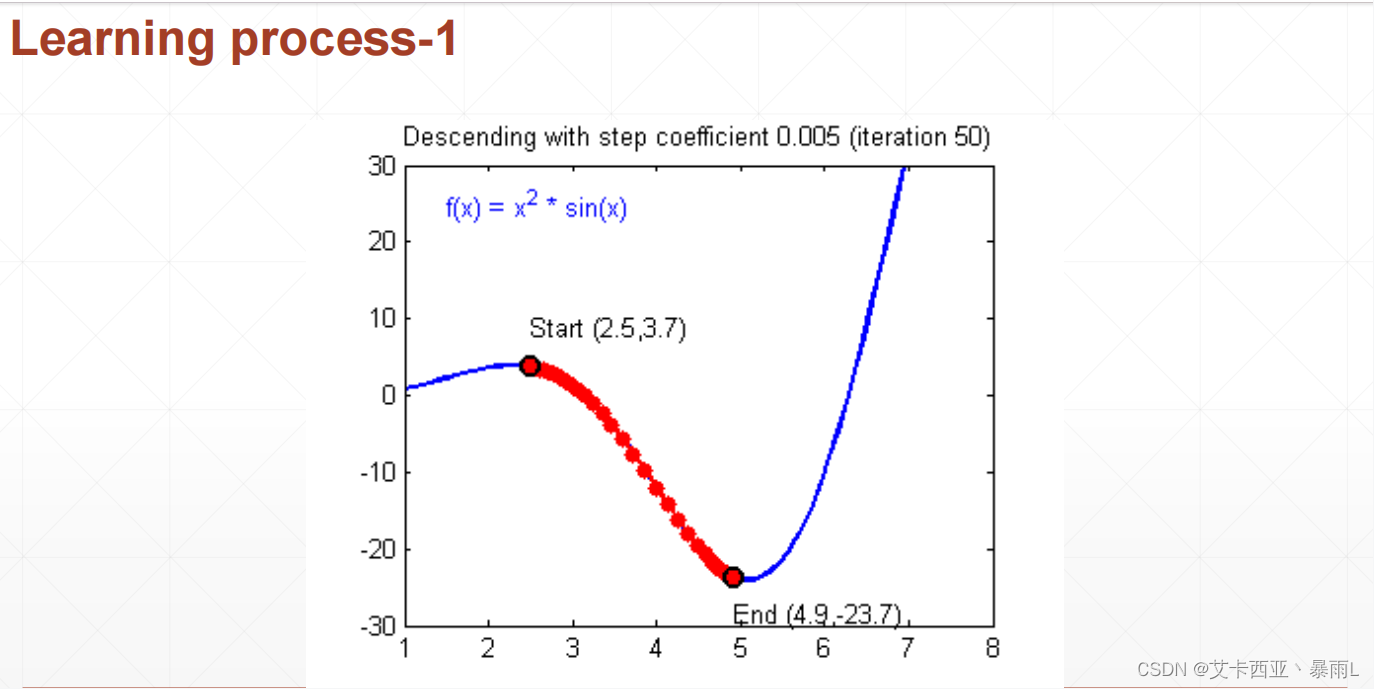
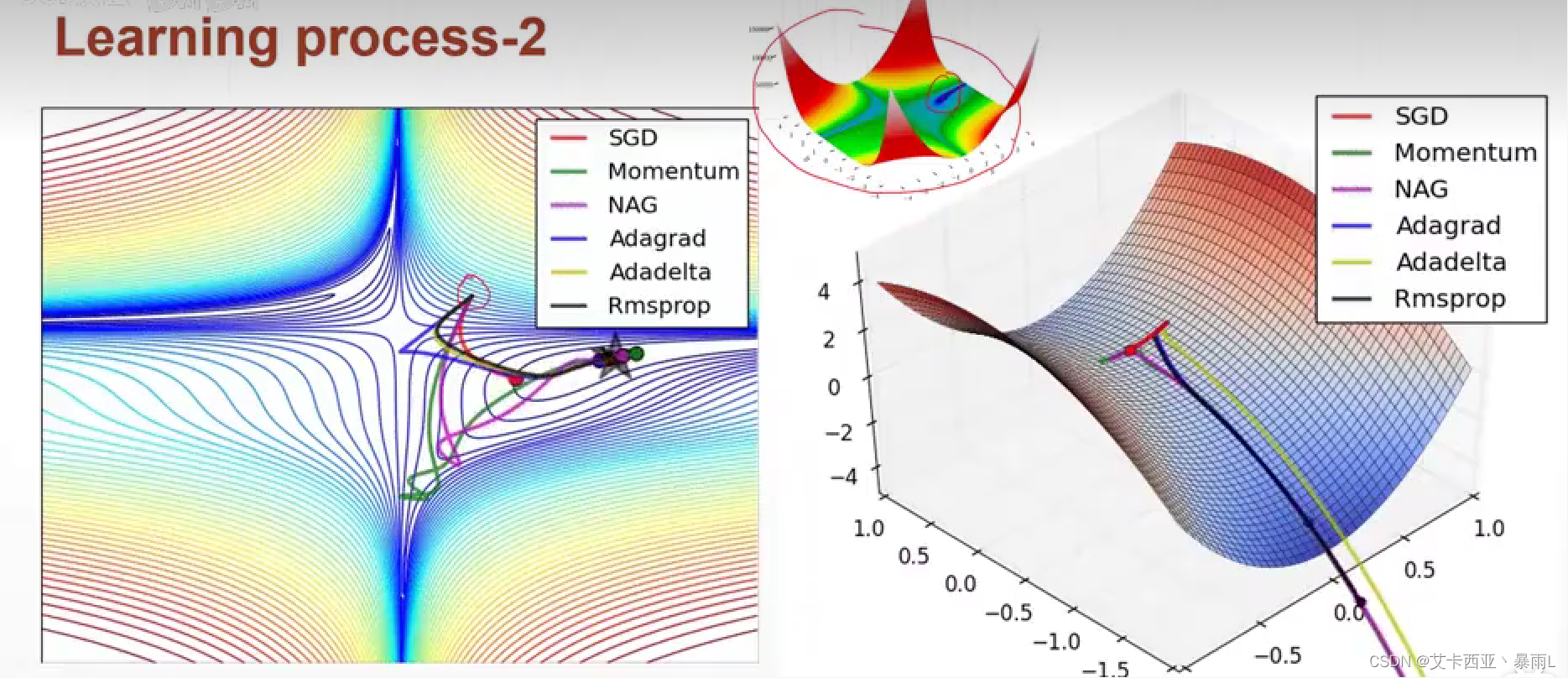
紅色是最原始版本的梯度下降來搜索會卡在馬鞍的點上

對于任何的一個點和另外的一個點,我們拉一條直線,這條直線中間的中點以及中點所對應的函數的值,例如定義為z1,z2且z1>z2,叫做凸函數,對于這種情況可以找到一個全局最優解
存在且不太常見的
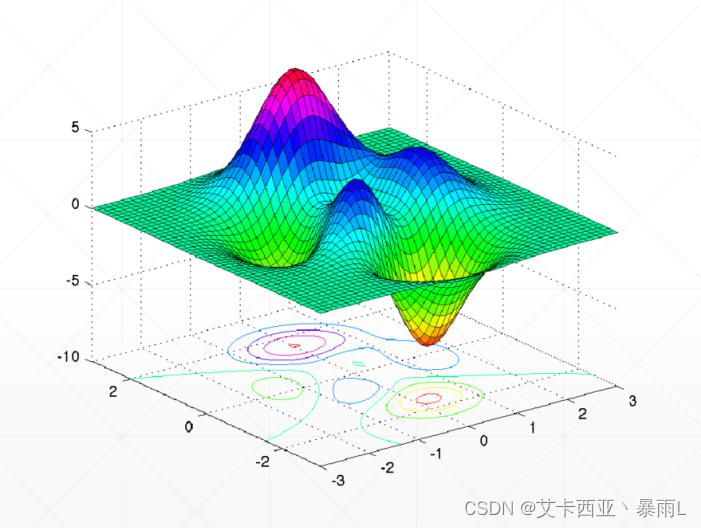
存在局部極大和局部極小,存在多個局部極小值
實際的例子:ResNet-56的平面

對于函數的輸出可能有無數多個w參數,對于ResNet可以有上千萬個W的參數f=(w1,w2,…),把上千萬的自變量可視化到一個二維的平面,可能會陷入到無數多的局部極小值中,即使有全局最小值解,因此對于一個深層次的神經網絡,取搜索的時候可能找到一個表現不滿意的因為此時的解可能是一個局部極小值解,因此網絡的精度不會特別高,Resnet加了一個shortcut的模塊,在神經網絡的旁邊加了一條支路,發現神經網絡可以變得很深同時也可以優化的很好,可視化后會變成第二個平面
使用梯度來搜索最小值的情況下,除了會遇到局部最小值,還可能遇到鞍點
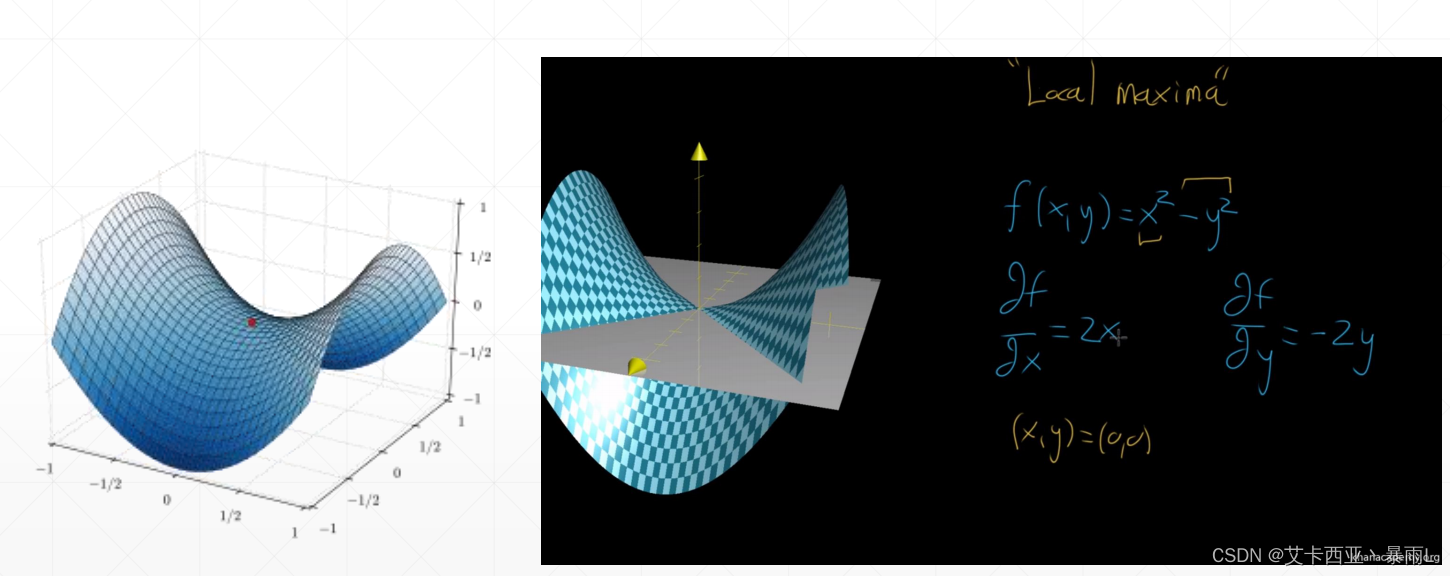
優化器表現
- 初始狀態
- 學習率
- 動量(即如何逃離局部極小值)
初始狀態
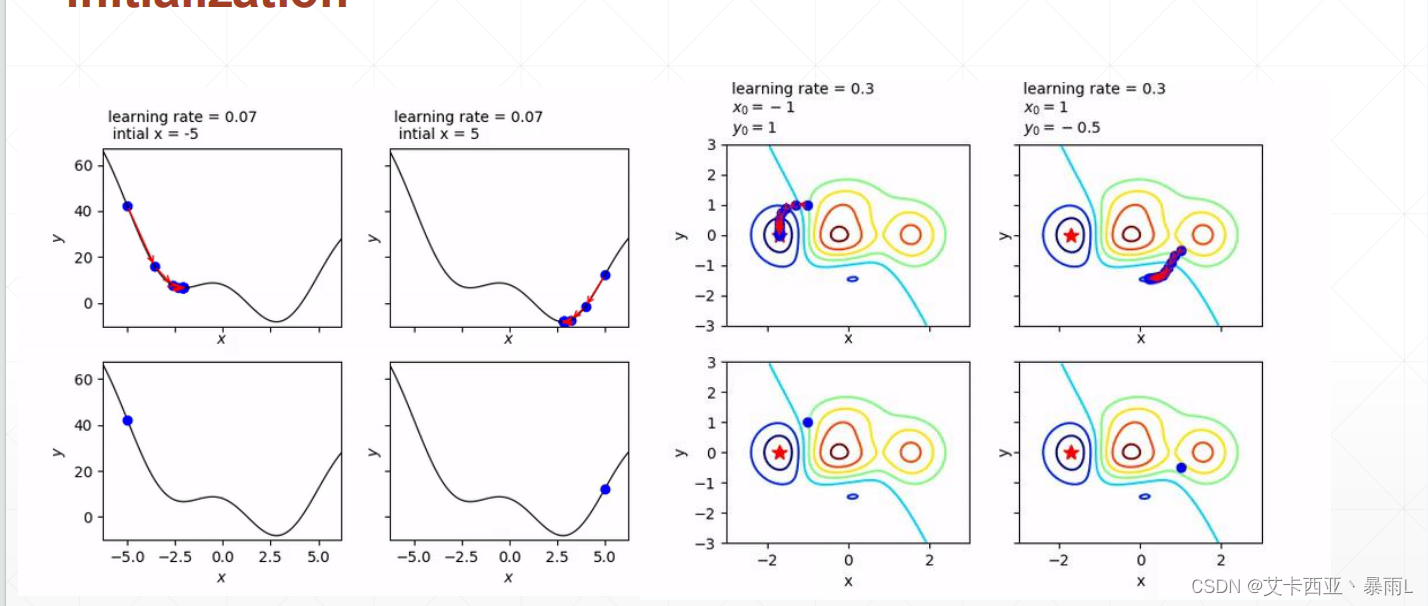
對于初始狀態的不同,會影響找到的是全局解還是局部極小值這樣的情況,搜索的路徑也可能不一樣,因此大家再做深度學習的時候函數的全職一定要初始化,而且初始化的時候如果沒有把握就按照目前主流的初始化的方法
上圖兩種初始化,左邊會到全局最小解,右邊會到局部極小值,不同的初始化狀態會得到不一樣的結果
學習率
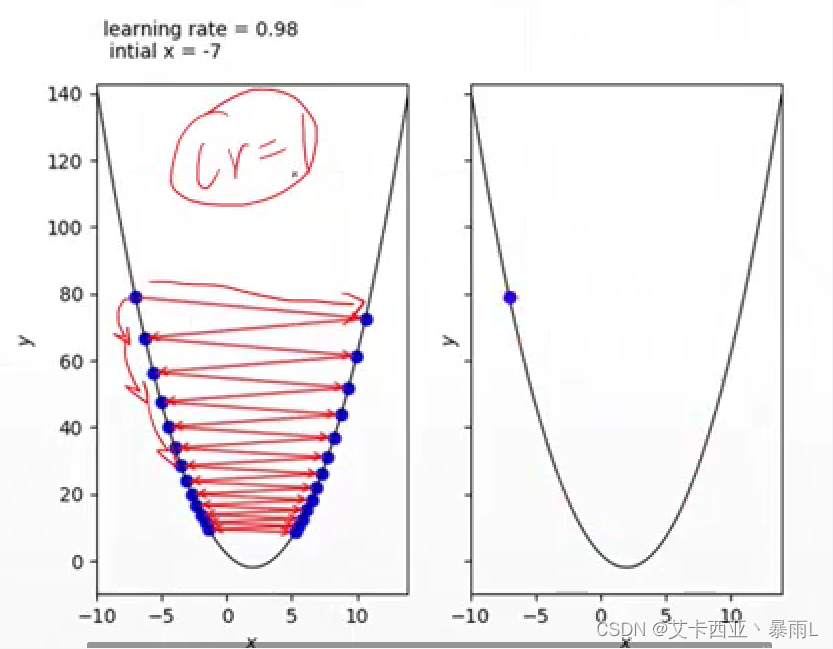
學習率設置為1的時候(比較大),步長會比較大,但實際上我們需要的情況是左邊藍色的點慢慢下降而不是左邊跳到右邊再跳到左邊,是因為學習率設置的過大,會一步跨的太長直接跨過了最小值,對于比較好的函數還可以慢慢震蕩到最小值,但是大部分現實情況是直接不收斂了,一開始要把learning rate設置的小一點,0.01或0.001這樣,如果發現收斂了可以試著大一點這樣會讓收斂的速度會快一點
學習率也會影響收斂的精度,例如到最小值附近learning rate還是很大會一直在附近震動永遠到不了最小值,只會得到一個近似比較好的情況,這種時候要慢慢減小learning rate
如何逃出局部最小值
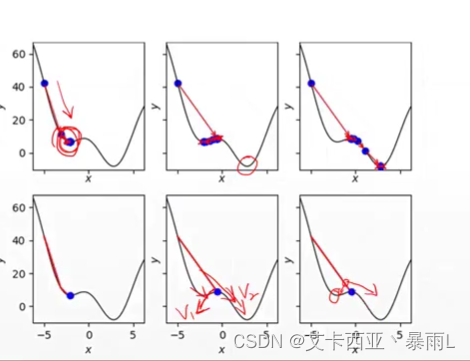
很有可能搜索到局部最小值就停止了,但是還有最小值,這時候可以添加一個動量,這個動量可以直觀的理解為慣性,也就是說在局部極小值左邊發現梯度呈現右下降的趨勢,在右邊發現梯度呈左下角的趨勢,如果在此時考慮一個慣性的話,在右邊的時候梯度會引導你回去到局部最小值,但是本來就是向右去降低梯度的,如果可以考慮到一個慣性的話,假設向右走是v1向量向左走是v2向量,把這兩個向量綜合一下就會得到一個朝向于偏向v2的方向
常見函數的梯度
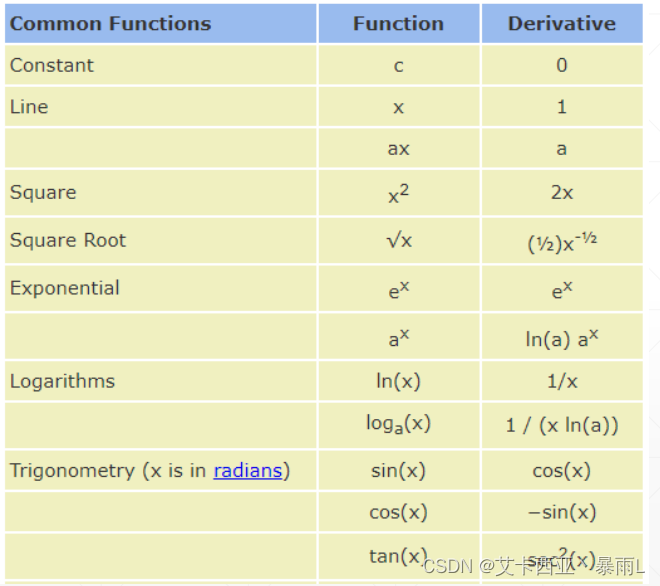
簡單感知機線性模型的求解

二次模型的梯度

指數求解梯度的方式

線性感知機的輸出和真實label之間的均方差

log函數求梯度
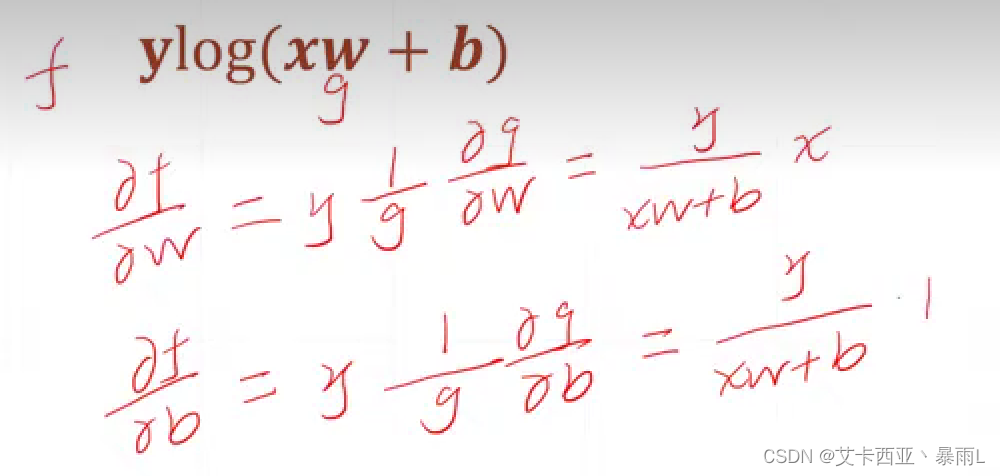





)





Hadoop集群安裝及MapReduce應用(手把手詳解版))




)

)
