第1章

統計學是收集、處理、分析、解釋數據并從數據中得出結論的科學。

統計學是處理數據的方法論。

參數 表示總體特征的概括性數字度量，是研究者想要了解的總體的某種特征值。

統計量 是用來描述樣本特征的概括性數字度量。

常用統計量包括：

（1）表示位置的統計量——樣本均值。

（2）表示離散程度的統計量——樣本標準差、樣本方差。

統計學中，經常用樣本統計量來估計總體參數。

統計學方法：

（1）描述統計學

（2）推斷統計學

管理統計學是應用于管理相關的領域的統計學理論和方法。

統計學在企業管理中所扮演的角色就是將原始數據轉換為有價值的信息的過程。

第2章 數據收集方法

定性數據：

定類尺度：是最低的計量尺度，按照屬性對事物進行分類，如品牌、性別等。

定類尺度：表現為類別，但不區分順序，

定序尺度：具有定類尺度的特征，能夠反映類別的等級，如成績等級、滿意度等；

定序數據表現為類別，有順序，

定距尺度：在定序尺度的基礎上，對事物類別或者次序之間間距的測度，沒有絕對零點，如溫度、海拔等。

定距數據表現為數值，可進行計算，

定比尺度：是最高的度量尺度，有絕度零點，如成績分數、收入等。

定比數據表現為數值，可進行加減乘除運算，

高層次數據類型具有低層次數據類型的一切特征，反之，未必。

適用于低層次數據的統計方法同樣適用于高層次數據類型。

第4章 描述數據的圖表方法

定性數據是只能歸于某一類別的非數字型數據，數據表現為類別。

定量數據是按數據尺度測量的觀測值，其結果表現為數值。

單變量定量數據，如每天的步數，一類產品的銷售價格。

多變量定量數據，如每天的運動時間及對應的消耗。

單變量定性數據：如考試成績等級

多變量定性數據：如期中考試和期末考試的成績等級。

定量數據的分組步驟：

（1）確定組數：K=1+logn/log2

（2）確定各組的組寬：

（3）

餅圖通常用來描述落在各類中的測量值數分別在總數中所占的比例，對于研究結構性問題相當有用。

環形圖

顯示具有相同分類且問題可比的多個樣本或總體中各類別所占的相應比例，對各總體進行比較研究。

在類別值為定序數據時這種比較才有意義。

交叉表

第4章 描述統計中的測度

測度：在數學分析里指一個函數，它對一個給定集合的某些子集指定一個數。

統計數據的測度主要分為：

集中趨勢測度：

反映一組數值向中心值靠攏的傾向，或表明一組統計數值所具有的一般水平。

離散趨勢測度：

反應各數據遠離其中心值的趨勢。

極差：表明數列中各變量值變動的范圍。R越大，表明數列中變量值變動的范圍越大，即數列中各變量值差異大。

極差只能說明兩個極端變量值的差異，不能反映各變量值的差異程度。

四分位差另一種離散趨勢測度。

離散趨勢測度揭示變量值的差異，反映總體各變量值遠離其平均數的趨勢。

離散趨勢測度和集中趨勢測度分別從不同的側面反映總體的數量特征。

、

形狀測度

第5章 概率與概率分布

第6章 抽樣與抽樣分布

為什么抽樣 ？

（1）總體容量太大、時間太長、成本太高。

（2）分析樣本統計量，可以認識總體的未知參數。

涉及到中心極限定理就會涉及到計算！！！

中心極限定理：從均值為μ方差為?的任意一個總體中抽取樣本容量為n的隨機樣本。當n充分大時，樣本均值的抽樣分布近似服從？？的正態分布。

當樣本容量n大于等于30，無論總體分布的形態如何，中心極限定理均適用。

在經濟管理中，經常使用樣本比例p推斷總體比例π

第七章 參數估計

參數估計的意義：

• 利用樣本的性質去推斷總體的性質
• 參數能夠提供刻畫總體性質的重要信息，當參數未知時，就要利用樣本對參數進行估計，進而獲得總體的信息
• 參數估計是在抽樣及抽樣分布的基礎上，根據樣本統計量來推斷所關心的總體參數，進而達到認識總體未知參數的目的

樣本統計量是什么？

樣本統計量（簡稱統計量）指的是樣本的函數，并且此函數不含未知參數。常見的統計量有：樣本均值，樣本方差等。

參數估計的分類：

• 點估計：矩估計、極大似然估計、最小二乘估計等
• 區間估計：總體均值估計、總體比例的區間估計等

什么是點估計？

使用樣本統計量估計參數值的方法稱為點估計。

原點矩和中心矩是什么呀？

• 用樣本的一階原點矩來估計總體的均值μ
• 用樣本的二階中心距來估計總體的方差

極大似然估計的原理是什么？

點估計的評價準則：

• 無偏性：雖然不同的樣本有不同的估計值，但反復抽取樣本并計算相應估計值，估計值的均值與真值相等，則為無偏估計量。所謂無偏性是指樣本估計量的數學期望等于被估計總體參數的真值。
• 有效性：兩個無偏估計量a，b，如果a的觀測值比b的觀測值更為集中于未知參數x的真值附近，則a比b更有效。
• 一致性：當樣本容量n趨于無窮大時，估計量依概率收斂于總體未知參數x。

點估計的優點是簡單，但是不能反映估計量的可信度和精度。

區間估計的關鍵術語：

• 置信區間：在點估計的基礎上，給出總體參數估計的一個區間范圍，該區間由樣本統計量加減抽樣誤差而得到的。
• 置信水平（1-α）：樣本統計量與總體參數的接近程度給出的概率量度。

區間估計的步驟！！！（計算！！！）

第八章 假設檢驗

假設檢驗和參數估計是統計推斷的兩個重要組成部分，它們都是利用樣本對總體進行某種推斷。

參數估計是用樣本統計量估計總體未知參數的方法。

假設檢驗也稱為顯著性檢驗，是事先做出一個關于總體參數的假設（H(0)），然后利用樣本信息來判斷原假設是否合理，從而決定是否接受原假設的統計推斷方法。

假設檢驗依據概率論中“在一次實驗中，小概率事件幾乎不發生”的原理。

顯著性水平：表示原假設H0 為真時拒絕H0 的概率，即拒絕原假設的風險，用α表示。

拒絕域：

假設檢驗：是事先做出一個關于參數的假設（H0）,然后利用樣本信息來判斷原假設是否合理，從而決定是否接受原假設的統計推斷方法。

假設檢驗依據概率論中“在一次實驗中，小概率事件幾乎不發生”的原理，即認為在一次實驗中小概率事件不可能發生。

假設檢驗的步驟：

提出原假設和備擇假設--->確定檢驗統計量--->確定接受域和拒絕域--->計算統計量與統計決策

假設檢驗需要借助樣本統計量進行統計推斷，即檢驗統計量。

不同的假設檢驗問題需要選擇不同的檢驗統計量。

選擇統計量需要考慮的因素包括但不僅限于：

（1）總體方差已知還是未知。

（2）單一總體還是兩個總體。

（3）用于進行檢驗的樣本是大樣本還是小樣本。

單側檢驗和雙側檢驗：

原假設檢驗是否相等（帶=號）的為雙側檢驗

帶有方向性的檢驗（明顯提高、減少）為單側檢驗

H0 :例如， μ>300為左側檢驗

第一類錯誤（棄真錯誤）：原假設H0 為真，但是由于樣本的隨機性使得樣本統計量落入拒絕域，由此做出拒絕原假設的錯誤判斷。

第二類錯誤（取偽錯誤）：

P值是指在原假設H0 為真時，所得樣本觀察結果更極端的結果出現的概率。

P值越小，拒絕原假設的理由越充分。

第9章 方差分析

方差分析是檢驗多個總體的均值是否相等的方法。其本質是研究變量之間的關系。

方差分析同時考慮所有的樣本，排除了錯誤累積的概率，更大程度上能夠避免拒絕正確的原假設。

方差分析：通過檢驗各種體的均值是否相等來判斷定類型自變量對數值型因變量是否有顯著影響。

因素水平：因素的不同表現。

觀測值：在每個因素水平下得到的樣本值。

從散點圖中可以看出，不同顏色飲料的銷售量有明顯差異，并且同一顏色飲料的銷售量也有明顯不同。

圖形不能證明不同顏色的銷量有顯著差異，也許這種差異是由樣本的隨機性造成的。

隨機誤差：因素的同一水平（總體）下，樣本各觀察值之間的差異。這種差異可以看成是隨機因素的影響，稱為隨機誤差。

組內誤差只含隨機誤差。

因素的不同水平（不同總體）下，各觀察值之間的差異可能是由于抽樣的隨機性所造成的，也可能是由于因素水平本身所造成的，后者所形成的誤差是由系統性因素造成的，稱為系統誤差。

組間誤差是隨機誤差和系統誤差的總和。

總離差平方和（SST）：全部數據x（ij）與總均值的差異。

組內離差平方和（SSE）：每組的每個數據x（ij）與該組均值的差異。

組間離差平方和（SSA）：各組的均值與總均值間的差異。

如果各因素水平的總體均值是相同的（顏色對銷售量沒有影響），那么組間誤差只包含隨機誤差，而沒有系統誤差。此時，組間離差平方和SSA與組內離差平方和SSE的比值就會接近1。

方差分析的目的：檢驗均值是否相等。

方差分析的思路：比較組內方差和組間方差。若兩者顯著不等，則均值不相等；否則，均值是相等的。

方差分析的方法：計算組件和組內方差比。

單因素方差分析的步驟：

提出假設：

單因素方差分析的目的是檢驗因素的k個水平的均值是否相等，因此提出如下形式的假設：

H(0)自變量對因變量沒有顯著影響。均值相等

H(1)自變量對因變量有顯著影響。

如果拒絕原假設，意味著自變量對因變量有顯著影響。

構造檢驗統計量：

（1）計算各樣本組的均值

（2）計算全部觀測值的總均值

（3）計算總離差平方和SST

（4）計算組間離差平方和SSA

（5）計算組內離差平方和SSE

（6）計算統計量

（7）構建檢驗統計量

統計決策

第 10 章 卡方分布和列聯分析

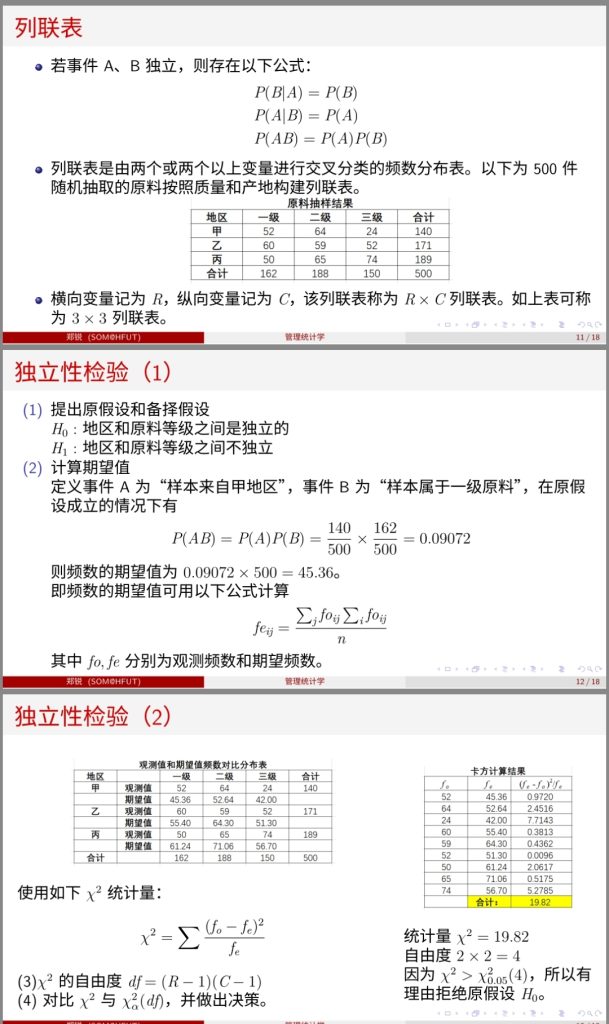
• 擬合優度檢驗

第11章 相關與回歸分析

• 相關系數的顯著性檢驗

一般情況下，總體的相關系數ρ是未知的，通常將樣本相關系數作為ρ的近似估值。為了考量樣本相關系數的可靠性，需要進行顯著性檢驗。

r的顯著性檢驗（t檢驗）

• 回歸方程的顯著性檢驗
• 回歸系數的顯著性檢驗

觀測值與其平均值的偏差平方和稱為總離差平方和，記為SST。

SST=SSR+SSE

回歸平方和SSR反映x的變化對y取值變化的影響；殘差平方和SSE反映除x以外的其他因素對y取值變化的影響。

相關系數r衡量的是兩個變量之間相關的強弱程度。

決定系數是相關系數的平方。它衡量的是變量y中有多大比例能用變量x來解釋。

第12章 時間序列分析與預測

時間序列分析

移動平均法

指數平滑法

線性趨勢預測

指數趨勢

多階曲線模型

多項式預測案例

自回歸預測模型

復合型序列的分解步驟：