目錄
二叉樹
樹的概念與結構
非樹形結構:
注意:
樹的相關術語
樹的表示
孩子兄弟表示法
樹形結構實際運用場景(拓展)
1.?文件系統管理
2.?數據庫與索引
3.?編程語言與數據結構
信息組織與展示
1.?思維導圖
2.?目錄與導航
3.?組織架構圖
網絡與通信
1.?路由算法
2.?XML/JSON 數據格式
二叉樹:
概念與結構
特點:
特殊的二叉樹
滿二叉樹
完全二叉樹?編輯
二叉樹的性質
二叉樹的存儲結構
順序存儲結構
鏈式存儲結構
實現順序結構二叉樹
堆的概念與結構
堆的特性:
?叉樹性質(左右孩子位置)
實現堆的順序結構
堆的結構體
核心函數功能
初始化
打印
交換數據
向上調整法
細節:
入堆
注意:
時間復雜度
判空
向下調整法
帶入實例:
時間復雜度
刪除堆頂元素:
獲取堆頂元素
堆的銷毀
測試代碼(堆排序---向下調整法建堆)
向上調整法建堆
步驟:
代碼實現(完整):
向上向下建堆方法時間復雜度
向下調整法
向上調整法
二叉樹
樹的概念與結構
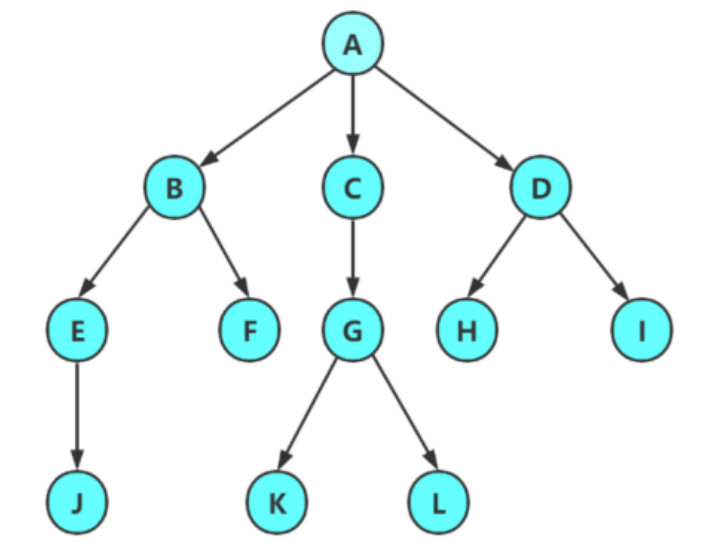
根節點:有一個特殊的結點,稱為根節點,即A,根節點沒有前驅節點
除根節點外,其余節點被分為互不相交的集合,且每個集合有結構與樹類似的子樹。子樹根節點有且只有一個前驅,有0個或者多個后繼。
非樹形結構:
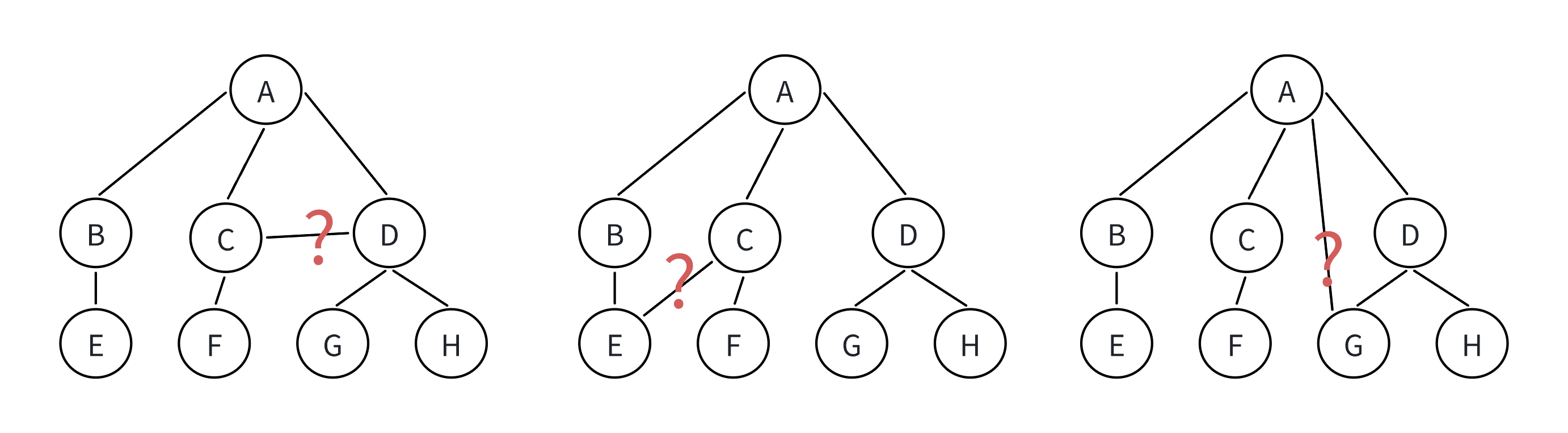
注意:
樹的相關術語
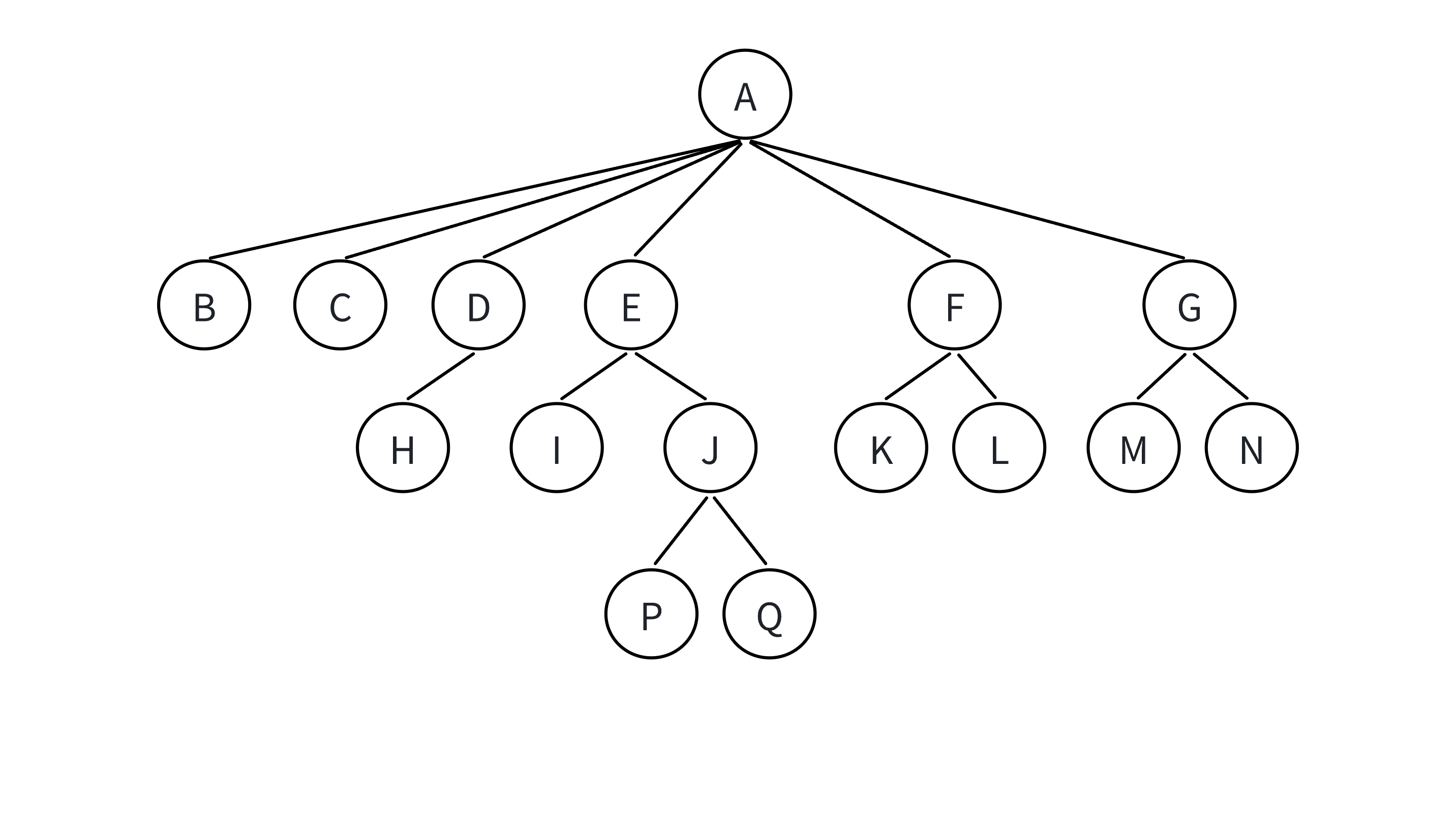
樹的表示
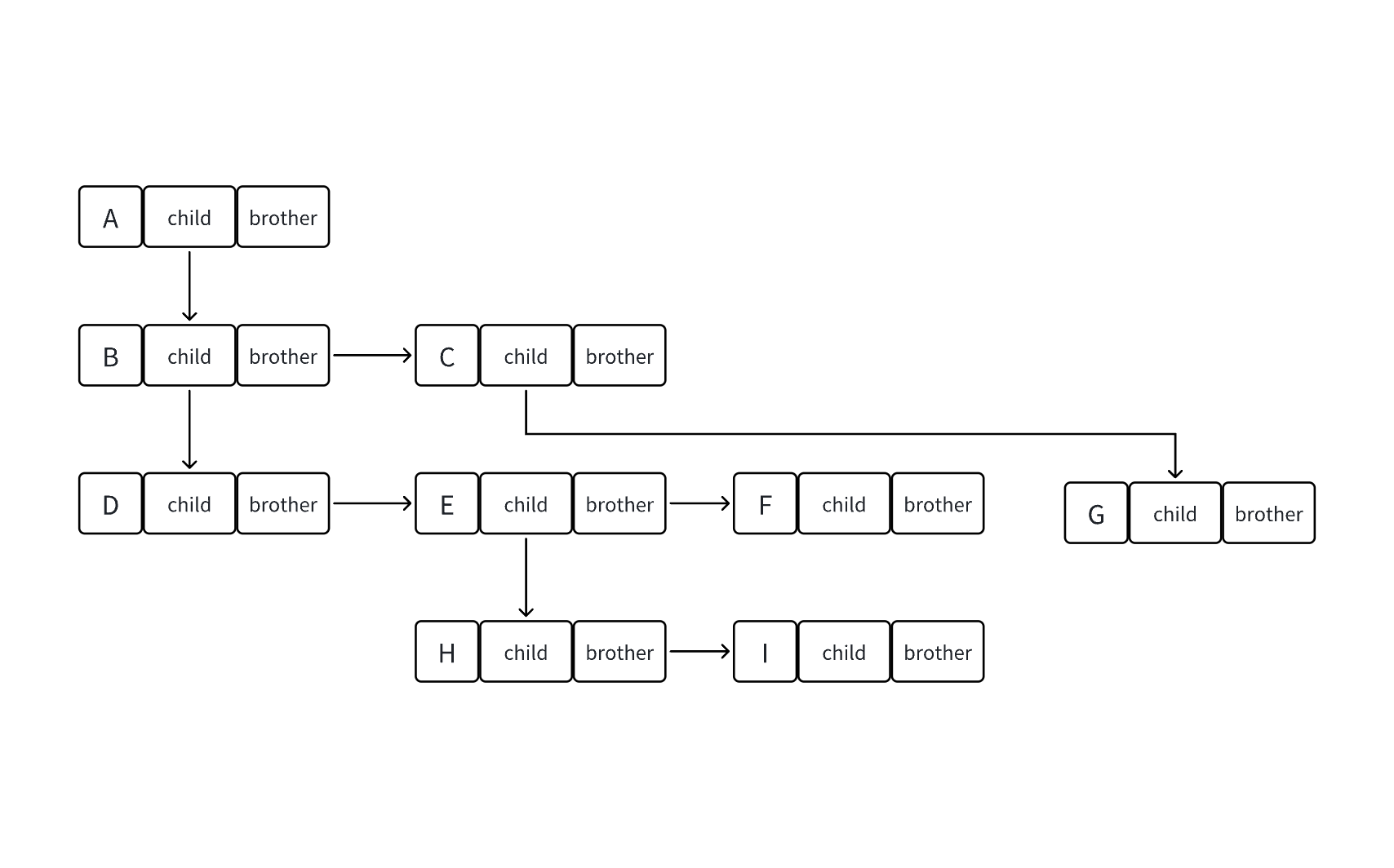
孩子兄弟表示法
struct TreeNode
{struct TreeNode* child;//左邊開始第一個孩子節點struct TreeNode* brother;//指向右邊的下一個兄弟結點int data;//存儲的數據
};
樹形結構實際運用場景(拓展)
1.?文件系統管理
- 操作系統(如 Windows、Linux)的文件目錄結構是最經典的樹形結構:
- 根目錄(如
C:\、/)為 “根節點”; - 子文件夾為 “中間節點”;
- 具體文件為 “葉子節點”。
- 根目錄(如
- 優勢:通過層級路徑(如
/user/doc/report.pdf)快速定位文件,支持遞歸遍歷和批量操作。
2.?數據庫與索引
- B 樹 / B + 樹:數據庫(如 MySQL)的索引結構,通過多層節點快速定位數據,平衡了查詢效率和磁盤存儲性能。
- 樹形查詢:用于表示數據庫中的 “父子關系”(如部門與子部門、評論與回復),通過遞歸查詢獲取完整層級數據。
3.?編程語言與數據結構
- 語法樹(AST):編譯器將代碼解析為樹形結構,用于語法分析和執行(如 Python、Java 的代碼執行過程)。
- DOM 樹:HTML/XML 文檔的解析結構,每個標簽為節點,支持通過 JavaScript 遍歷或修改頁面元素(如
document.getElementById)。 - 紅黑樹 / AVL 樹:高效的平衡查找樹,用于實現
TreeMap(Java)或map(C++)等數據結構,支持 O (log n) 的插入、刪除和查詢。
信息組織與展示
1.?思維導圖
- 以核心主題為根節點,分支延伸子主題,用于 brainstorming、知識梳理(如 XMind、MindNode 工具)。
2.?目錄與導航
- 書籍的章節結構、網站的導航菜單(如電商網站的 “商品分類→子分類→商品”),通過層級關系幫助用戶快速定位信息。
3.?組織架構圖
- 企業或機構的層級關系(如 “CEO→部門經理→員工”),清晰展示上下級隸屬關系。
網絡與通信
1.?路由算法
- 網絡中的路由表常以樹形結構表示,通過最短路徑算法(如 Dijkstra)在節點間傳遞數據,減少冗余路徑。
2.?XML/JSON 數據格式
-
半結構化數據的嵌套結構本質是樹形(如 JSON 的
{ "a": { "b": "c" } }),便于存儲層級化信息(如配置文件、API 返回數據)。
二叉樹:
概念與結構
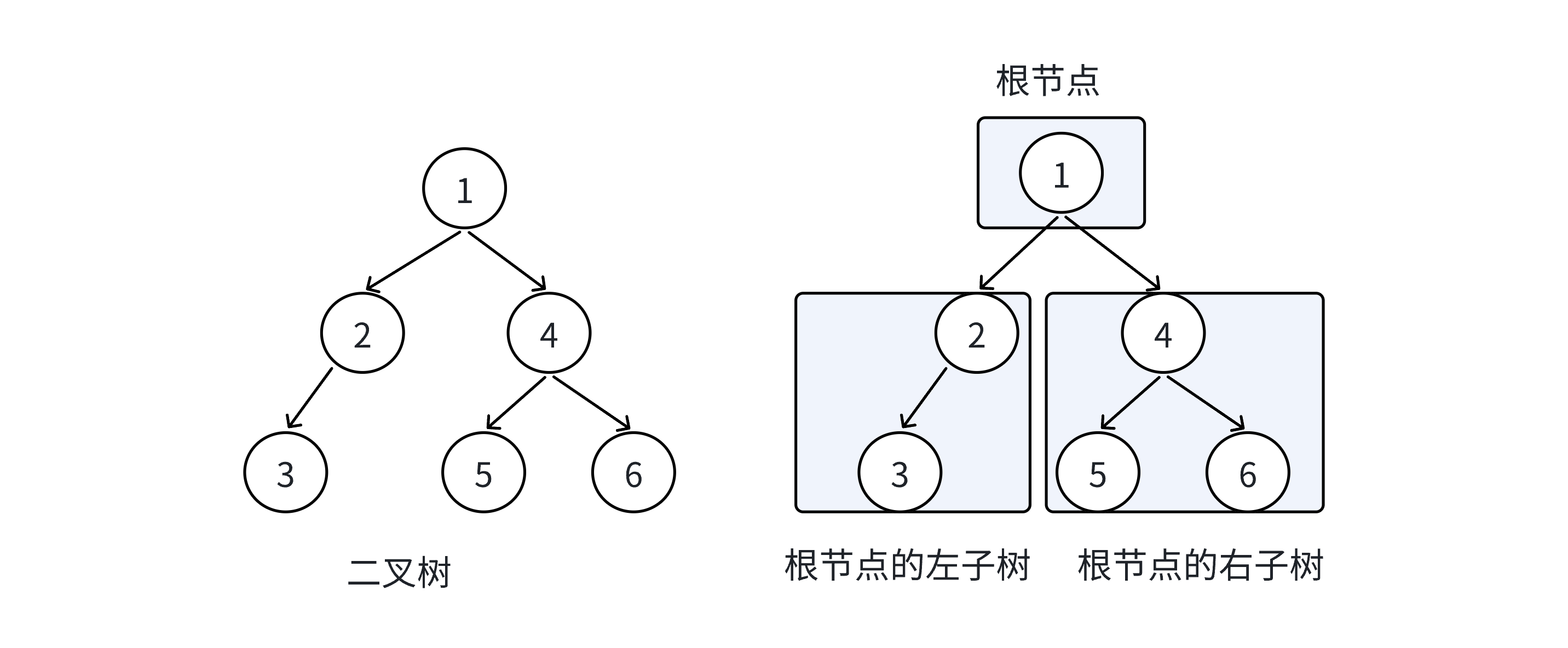
特點:
1.二叉樹不存在度大于2的結點
2.二叉樹子樹有左右之分,次序不能顛倒,是有序樹
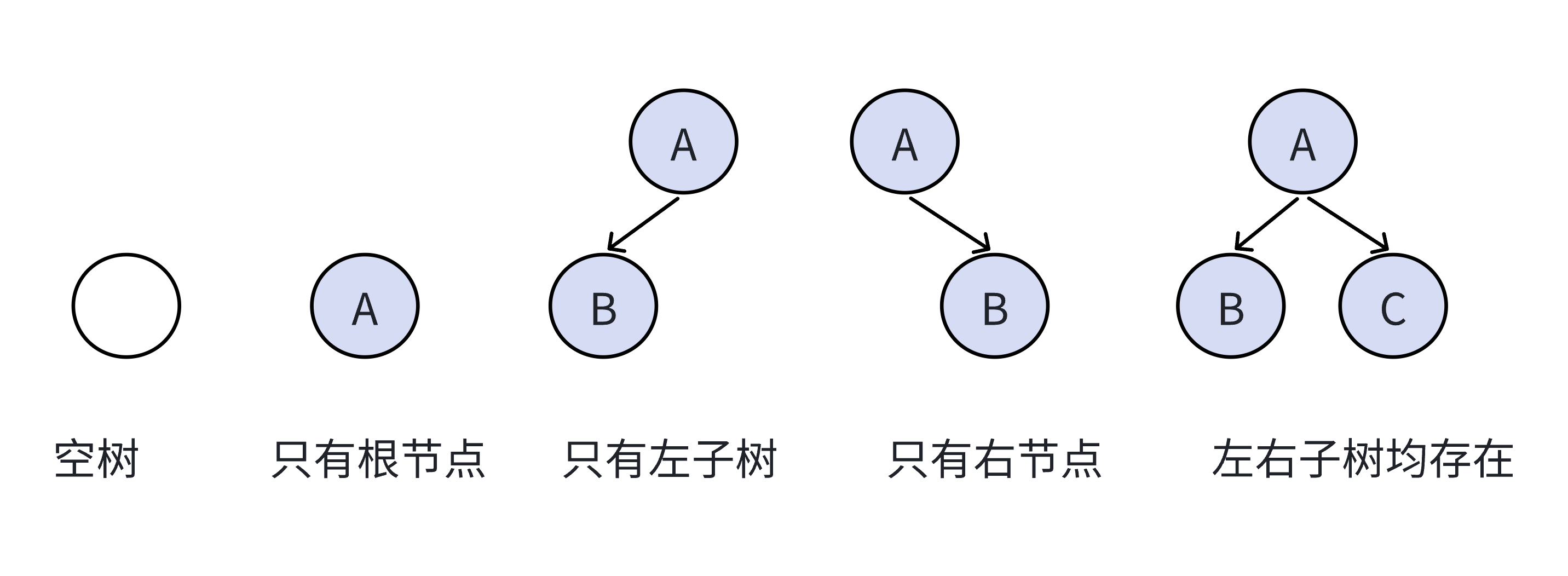
特殊的二叉樹
滿二叉樹
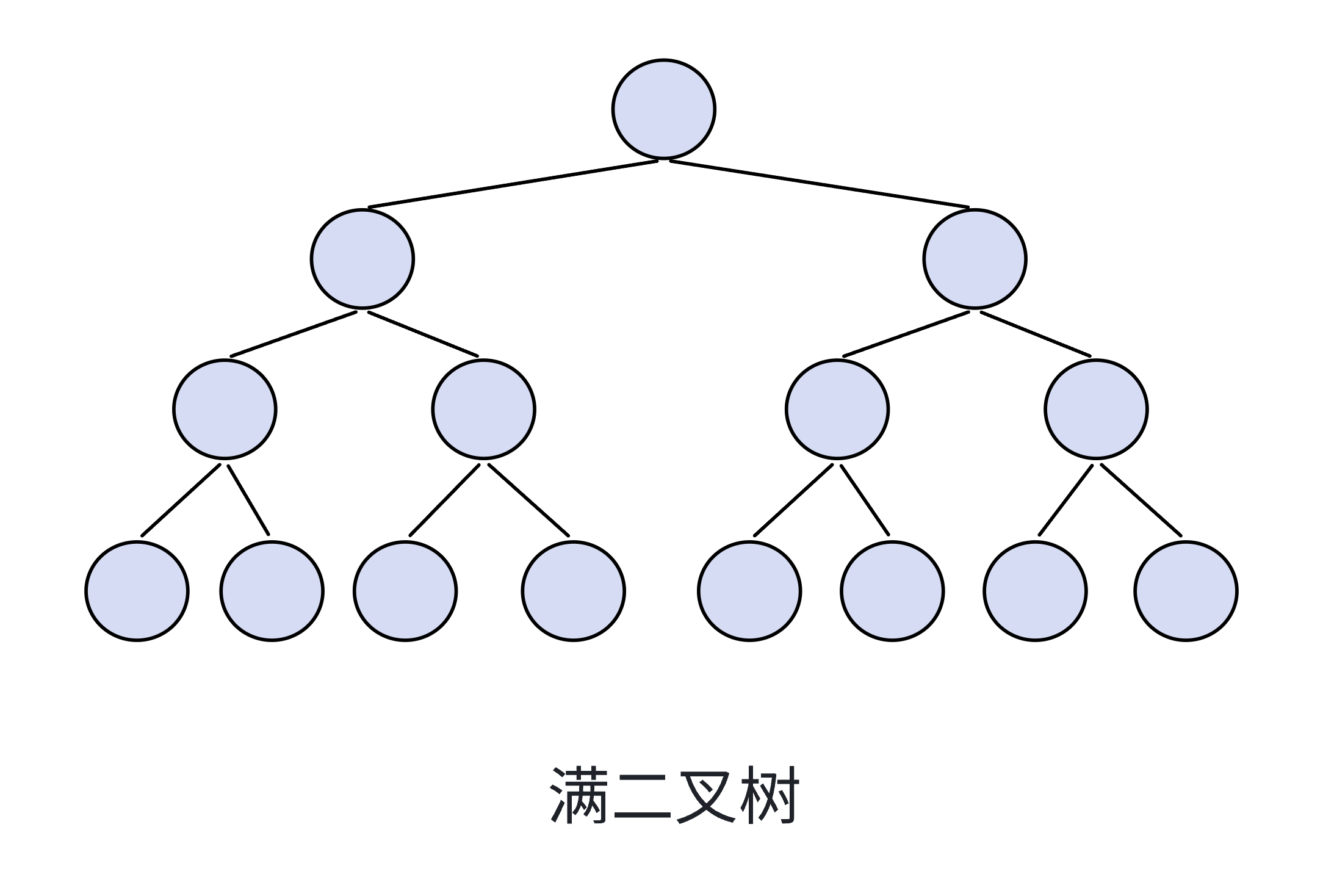
其層數若為n ,則節點數有2^n-1個
完全二叉樹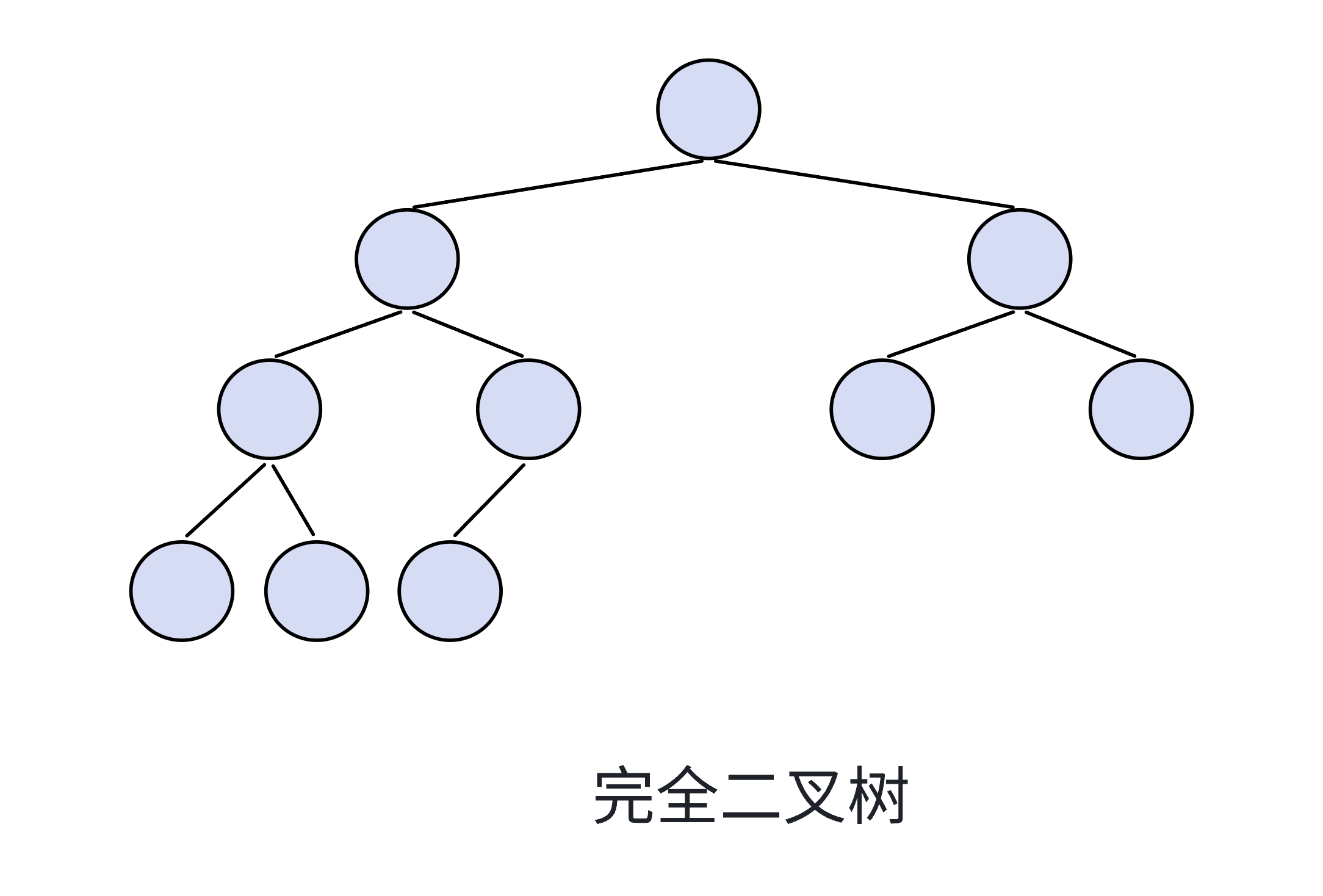

二叉樹的性質
二叉樹的存儲結構
順序存儲結構
順序存儲結構使用數組(或列表)來存儲二叉樹的節點,通過節點在數組中的位置關系來體現二叉
樹的邏輯結構。
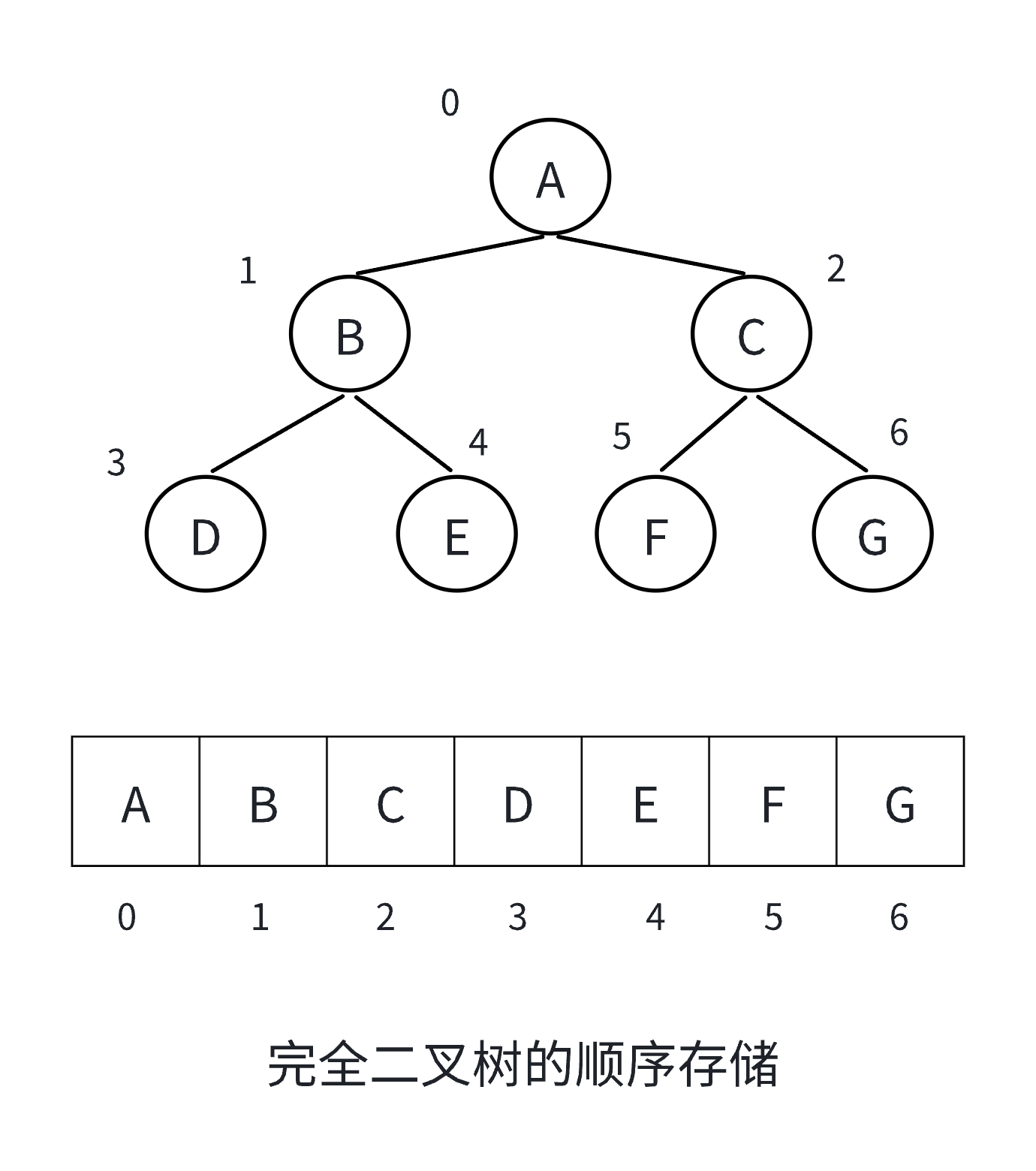
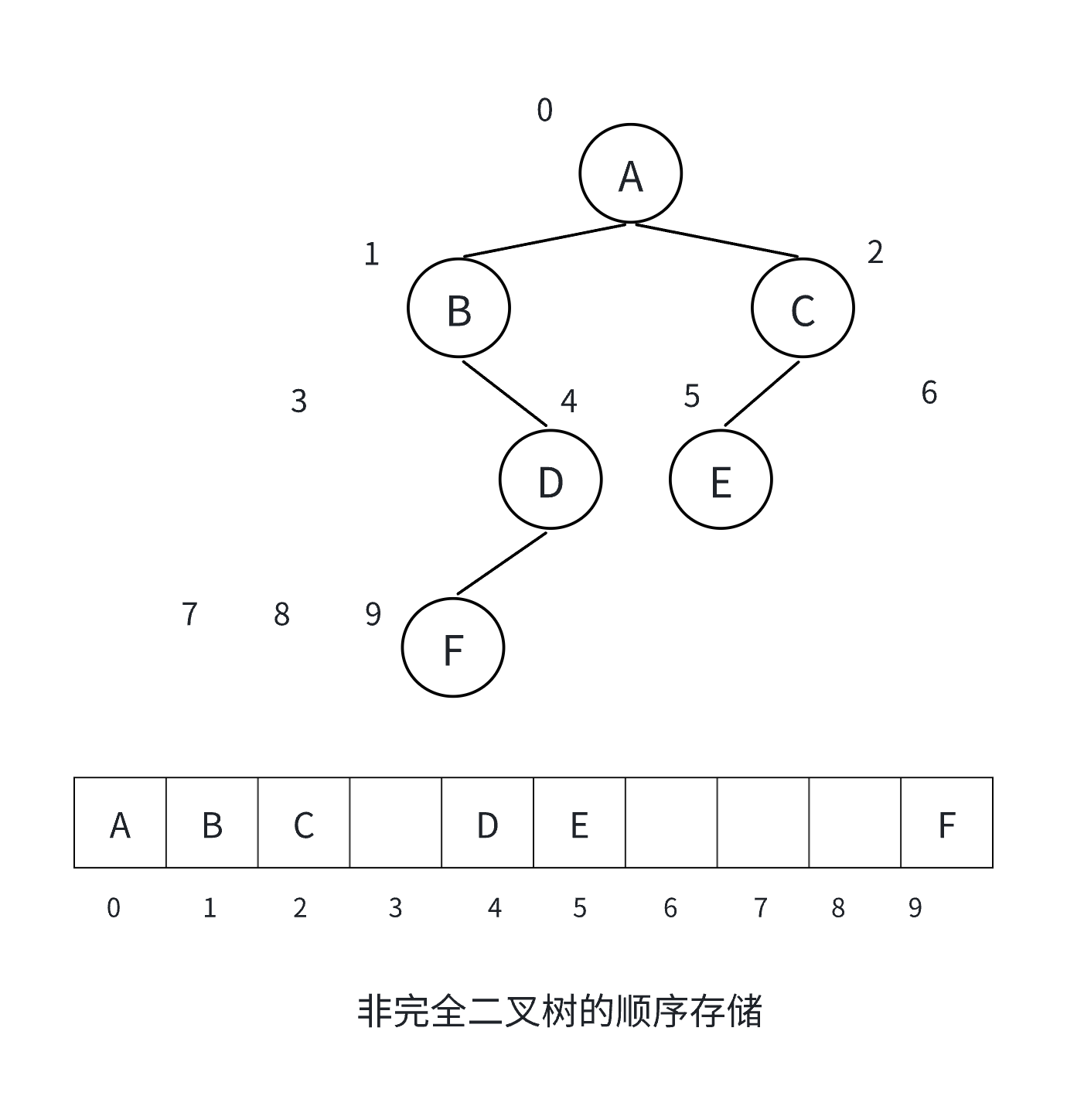
若根節點存儲在數組下標為?i?的位置:
- 左孩子節點存儲在?
2i + 1?的位置 - 右孩子節點存儲在?
2i + 2?的位置
優缺點:
- 優點:訪問節點速度快,通過索引可直接訪問,節省存儲空間(無需存儲指針)
- 缺點:只適合存儲完全二叉樹,對于非完全二叉樹會浪費大量空間;插入和刪除操作不方便
鏈式存儲結構
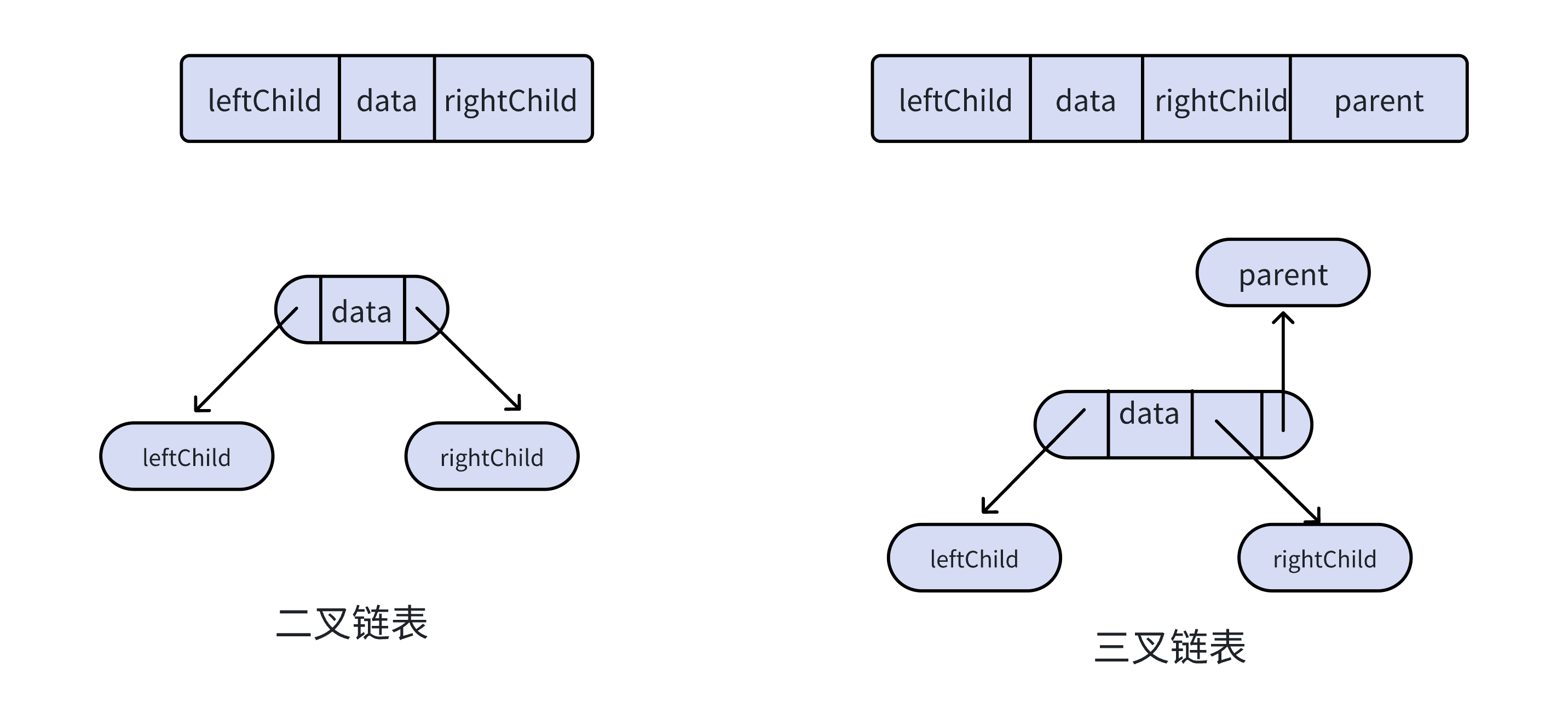
優缺點:
- 優點:空間利用率高,適合存儲各種形態的二叉樹;插入和刪除操作靈活方便
- 缺點:訪問節點需要通過指針遍歷,訪問效率相對較低;需要額外存儲空間存儲指針
實現順序結構二叉樹
堆的概念與結構
堆的特性:
- 結構特性:堆是一棵完全二叉樹,即除最后一層外,其他層的節點都被填滿,且最后一層的節點從左到右依次排列
- 堆序特性:
- 大根堆(Max Heap):每個父節點的值大于或等于其左右孩子節點的值
- 小根堆(Min Heap):每個父節點的值小于或等于其左右孩子節點的值
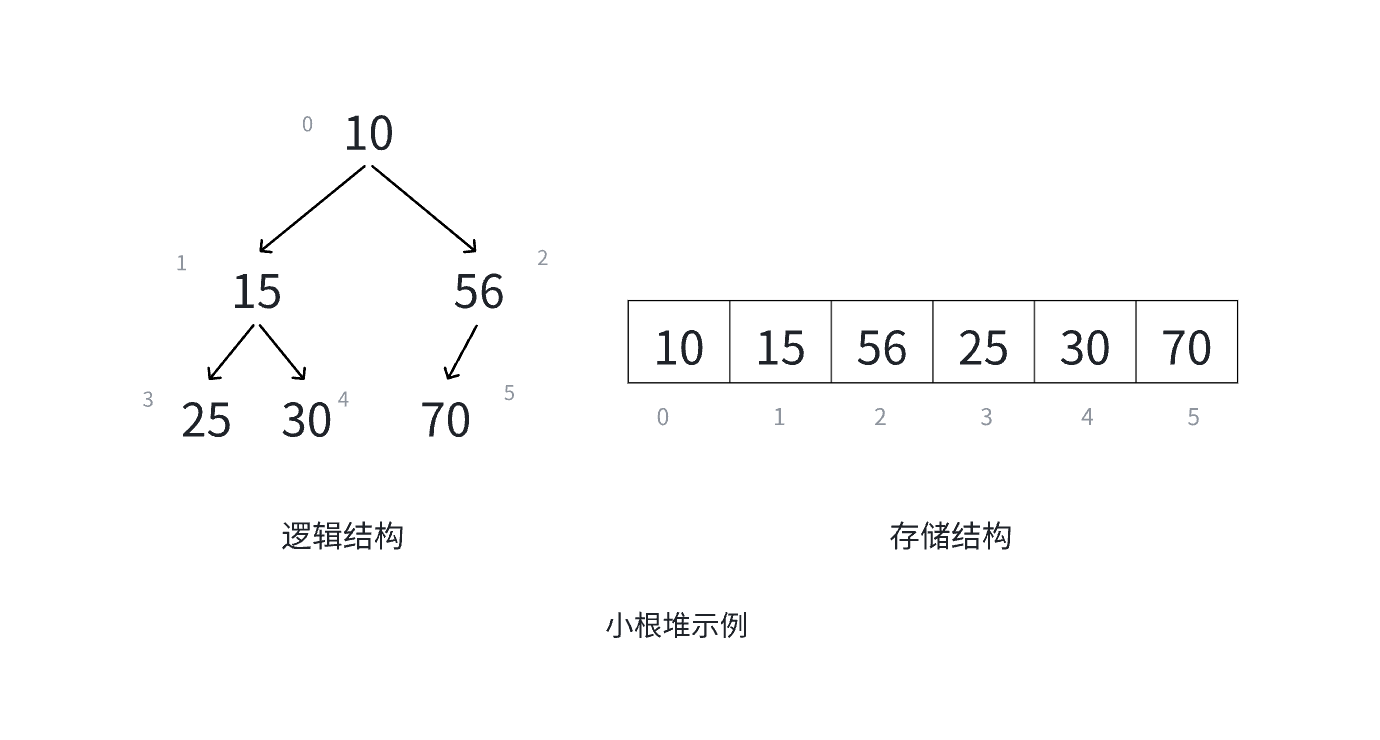
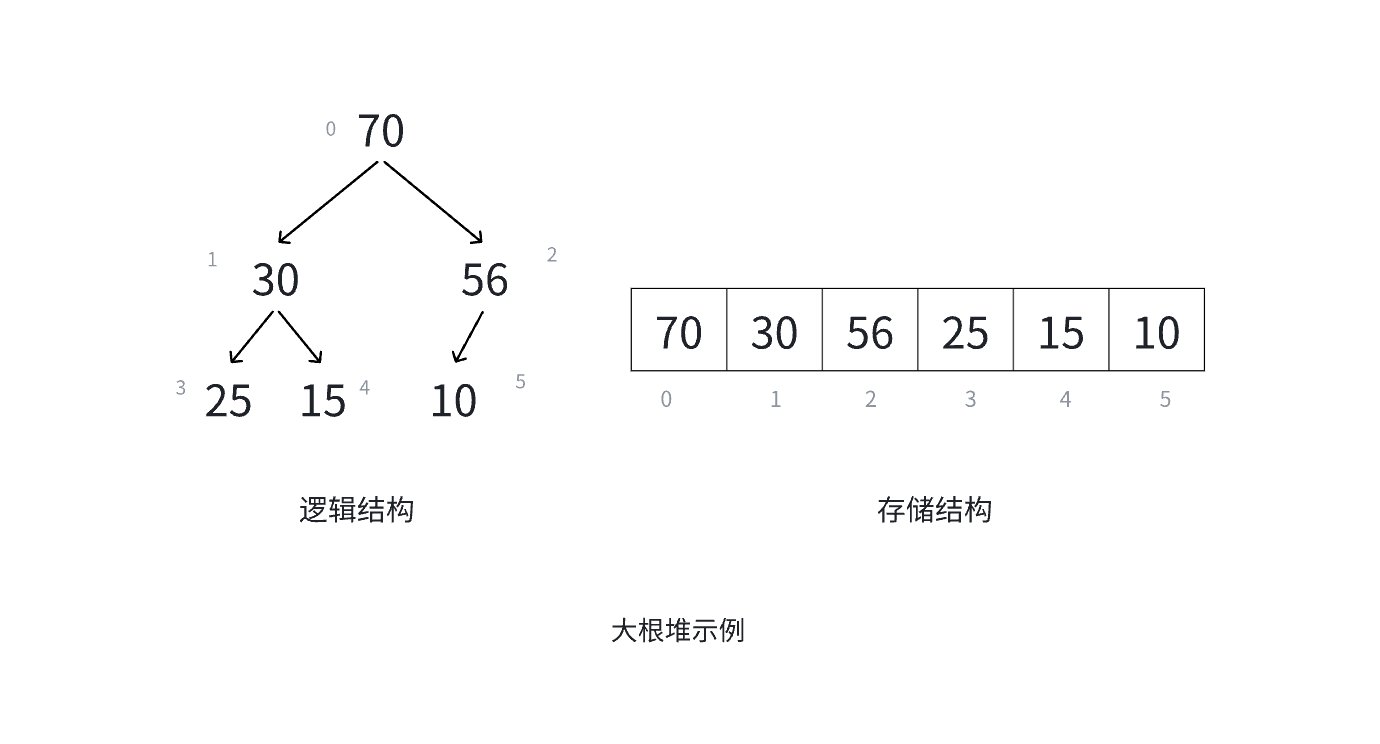
?叉樹性質(左右孩子位置)
實現堆的順序結構
堆的結構體
typedef int HPDataType; // 堆中存儲的數據類型
typedef struct Heap {HPDataType* arr; // 存儲堆元素的數組int size; // 當前堆中元素的數量int capacity; // 堆的容量
} HP;核心函數功能
HPInit:初始化堆,將數組指針置空,大小和容量設為 0HPDestroy:銷毀堆,釋放動態分配的內存HPPrint:打印堆中的所有元素Swap:交換兩個整數的值AdjustUp:向上調整算法,用于插入元素后維持堆的性質HPPush:向堆中插入元素HPEmpty:判斷堆是否為空AdjustDown:向下調整算法,用于刪除元素后維持堆的性質HPPop:刪除堆頂元素HPTop:獲取堆頂元素的值
void HPInit(HP* php);
void HPDestroy(HP* php);
void HPPrint(HP* php);void Swap(int* x, int* y);
void AdjustUp(HPDataType* arr, int child);
void AdjustDown(HPDataType* arr, int parent, int n);void HPPush(HP* php, HPDataType x);
void HPPop(HP* php);
//取堆頂數據
HPDataType HPTop(HP* php);// 判空
bool HPEmpty(HP* php);初始化
void HPInit(HP* php)
{php->arr = NULL;php->size = php->capacity = 0;
}
打印
void HPPrint(HP* php)
{for (int i = 0; i < php->size; i++){printf("%d ", php->arr[i]);}printf("\n");
}
交換數據
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}
如果不用指針,直接傳遞變量的值,函數內部的交換操作不會影響到函數外部的變量
向上調整法
void AdjustUp(HPDataType* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){//大堆:>//小堆:<if (arr[child] > arr[parent]){//調整Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}else {break;}}
}
當新元素被插入到堆的末尾時,可能會破壞堆的性質(父節點值大于子節點值)。AdjustUp?函數通過將新插入的元素(從最后一個位置)向上移動,與父節點比較并交換,直到重新滿足堆的性質。
細節:
-
父節點索引計算公式?
(child - 1) / 2?是由完全二叉樹的性質決定的 -
循環終止條件?
child > 0?確保不會越界訪問(根節點沒有父節點) -
若要實現小根堆,只需將比較運算符?
>?改為?<
入堆
//入堆
void HPPush(HP* php, HPDataType x)
{assert(php);//判斷空間是否足夠if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->arr, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail!");exit(1);}php->arr = tmp;php->capacity = newCapacity;}php->arr[php->size] = x;//向上調整AdjustUp(php->arr, php->size);++php->size;
}
- 新元素先放在數組末尾(對應完全二叉樹的最后一個位置)
- 調用
AdjustUp函數向上調整,確保插入后仍滿足堆的性質 - 最后更新堆的元素數量
注意:
realloc?的核心作用是重新分配已有的動態內存塊,可以:
- 當原內存塊后面有足夠空間時,直接在原地擴展,無需復制數據
- 當空間不足時,自動分配新內存塊并將原數據復制過去
而?malloc?只能分配全新的內存塊,如果用?malloc?實現擴容,需要手動完成 - 當堆的內存塊后面有連續的空閑空間時,
realloc?可以直接擴展內存,避免數據復制,效率遠高于?malloc?+?memcpy?+?free?的組合。
時間復雜度
- 擴容操作的時間復雜度:O (n)(最壞情況,需要復制所有元素),但由于采用 2 倍擴容策略,平均下來是 O (1)
- 向上調整操作的時間復雜度:O (log n)(最多需要調整到根節點,路徑長度為堆的高度)
- 因此,
HPPush操作的平均時間復雜度為 O (log n)。
判空
// 判空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}
向下調整法
//向下調整算法
void AdjustDown(HPDataType* arr, int parent, int n)
{int child = parent * 2 + 1;//左孩子while (child < n){//大堆:<//小堆:>if (child + 1 < n && arr[child] < arr[child + 1]){child++;}//大堆: >//小堆:<if (arr[child] > arr[parent]){//調整Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}
HPDataType* arr:存儲堆元素的數組int parent:需要向下調整的起始父節點索引(通常是堆頂元素索引 0)int n:堆中有效元素的個數(調整范圍不超過此值)-
關鍵細節:
- 先判斷右孩子是否存在且更大(
child + 1 < n確保不越界),目的是找到兩個孩子中的最大值 - 若子節點大于父節點,交換后繼續向下調整;否則說明已滿足堆性質,停止調整
- 若要實現小根堆,只需將兩處比較運算符
<和>分別改為>和<
- 先判斷右孩子是否存在且更大(
帶入實例:
假設大根堆當前狀態為?[60, 50, 40, 30],刪除堆頂元素后,最后一個元素30移到堆頂,數組變為?[30, 50, 40, ...](size減 1 后n=3):
時間復雜度
AdjustDown的時間復雜度為O(log n),因為最多需要調整到堆的最底層,路徑長度為堆的高度(完全二叉樹的高度為log2(n+1))。
parent=0,child=1(左孩子 50)- 右孩子
child+1=2(值 40)存在,50>40,所以child保持 1 - 子節點 50 > 父節點 30,交換后數組為?
[50, 30, 40],parent=1,child=3 child=3不小于n=3,循環終止,調整完成,結果為?[50, 30, 40],滿足大根堆性質
刪除堆頂元素:
void HPPop(HP* php)
{assert(!HPEmpty(php));// 0 php->size-1Swap(&php->arr[0], &php->arr[php->size - 1]);--php->size;//向下調整AdjustDown(php->arr, 0, php->size);
}
- 時間復雜度:O (log n),主要由
AdjustDown操作決定 - 空間復雜度:O (1),僅使用常數級額外空間
獲取堆頂元素
//取堆頂數據
HPDataType HPTop(HP* php)
{assert(!HPEmpty(php));return php->arr[0];
}堆的銷毀
void HPDestroy(HP* php)
{if (php->arr)free(php->arr);php->arr = NULL;php->size = php->capacity = 0;
}
測試代碼(堆排序---向下調整法建堆)
void arrPrint(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}
void BubbleSort(int* arr, int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){Swap(&arr[j], &arr[j + 1]);}}}
}//堆排序
void HeapSort1(int* arr, int n)
{HP hp; //——————借助數據結構堆來實現堆排序HPInit(&hp);for (int i = 0; i < n; i++){HPPush(&hp, arr[i]);}int i = 0;while (!HPEmpty(&hp)){int top = HPTop(&hp);arr[i++] = top;HPPop(&hp);}HPDestroy(&hp);
}void HeapSort(int* arr, int n)
{//建堆——向下調整算法建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, i, n);}//堆排序int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, 0, end);end--;}}void test01()
{HP hp;HPInit(&hp);HPPush(&hp, 56);HPPush(&hp, 10);HPPush(&hp, 15);HPPush(&hp, 30);//HPPush(&hp, 70);//HPPush(&hp, 25);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPDestroy(&hp);
}void test02()
{HP hp;HPInit(&hp);HPPush(&hp, 56);HPPush(&hp, 10);HPPush(&hp, 15);HPPush(&hp, 30);HPPrint(&hp);while (!HPEmpty(&hp)){int top = HPTop(&hp);printf("%d ", top);HPPop(&hp);}HPDestroy(&hp);
}int main()
{//test01();//test02();int arr[6] = { 19,15,20,17,13,10 };printf("排序之前:");arrPrint(arr, 6);//堆排序HeapSort(arr, 6);printf("排序之后:");arrPrint(arr, 6);return 0;
}

向上調整法建堆
將元素逐個插入堆中,每次插入后通過 “向上調整” 操作,確保新元素與父節點的關系符合堆的性質(最小堆中父節點值小于等于子節點值;最大堆中父節點值大于等于子節點值)。
步驟:
- 插入新元素:將新元素暫時放在堆的末尾(數組的最后一個位置)。
- 向上調整:比較新元素與其父節點的值,若不符合堆的性質(如最大堆中,新元素 >?父節點),則交換兩者位置。
- 重復調整:繼續將新元素與其新的父節點比較,直到新元素的父節點符合堆的性質,或新元素成為根節點(此時無法再向上調整)。
代碼實現(完整):
#include <stdio.h>// 交換兩個元素
void Swap(int* a, int* b) {int temp = *a;*a = *b;*b = temp;
}// 向上調整算法(用于建堆)
// 假設構建的是最大堆
void AdjustUp(int* arr, int child) {int parent = (child - 1) / 2;// 當子節點索引大于0且子節點值大于父節點值時,需要調整while (child > 0) {if (arr[child] > arr[parent]) {Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;} else {// 符合最大堆性質,無需繼續調整break;}}
}// 向下調整算法(用于堆排序過程中維持堆性質)
// 假設構建的是最大堆
void AdjustDown(int* arr, int parent, int n) {int child = 2 * parent + 1; // 左孩子索引while (child < n) {// 選擇左右孩子中值較大的那個if (child + 1 < n && arr[child + 1] > arr[child]) {child++;}// 如果父節點值小于子節點值,交換它們if (arr[parent] < arr[child]) {Swap(&arr[parent], &arr[child]);parent = child;child = 2 * parent + 1;} else {// 符合最大堆性質,無需繼續調整break;}}
}// 堆排序函數
void HeapSort(int* arr, int n) {if (arr == NULL || n <= 1) {return; // 空數組或只有一個元素無需排序}// 建堆----向上調整法建堆for (int i = 0; i < n; i++) {AdjustUp(arr, i);}// 堆排序int end = n - 1;while (end > 0) {// 將堆頂元素(最大值)與末尾元素交換Swap(&arr[0], &arr[end]);// 調整剩余元素為最大堆AdjustDown(arr, 0, end);end--;}
}// 測試函數
int main() {int arr[] = {3, 1, 4, 1, 5, 9, 2, 6};int n = sizeof(arr) / sizeof(arr[0]);printf("排序前: ");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");HeapSort(arr, n);printf("排序后: ");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}
改變點:
向上向下建堆方法時間復雜度
向下調整法
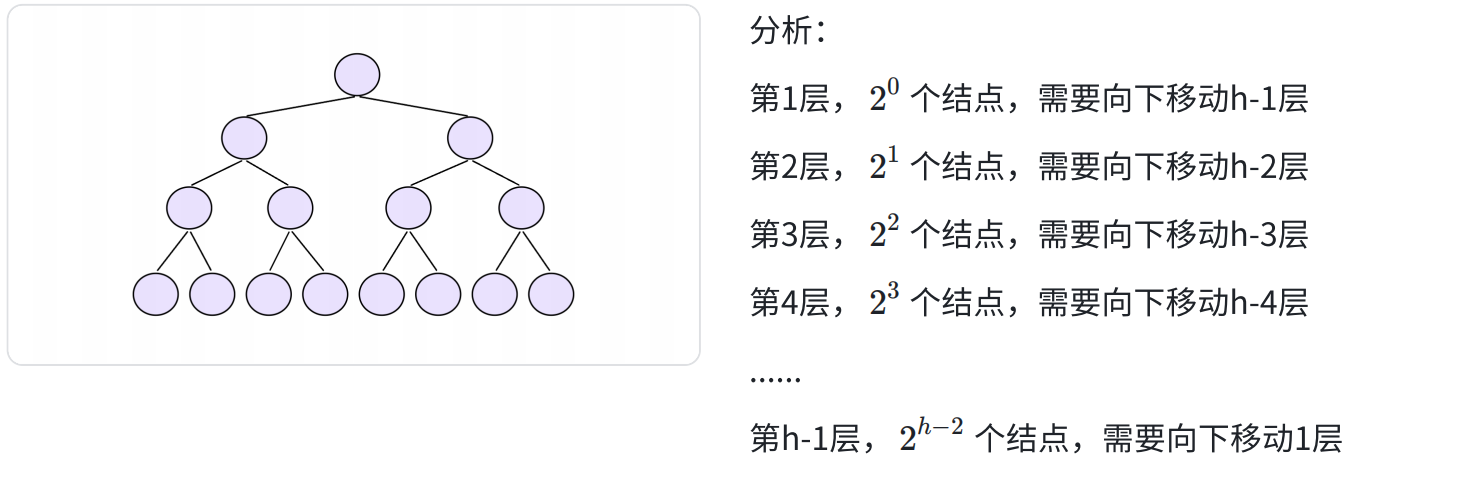
相關計算:
向上調整法
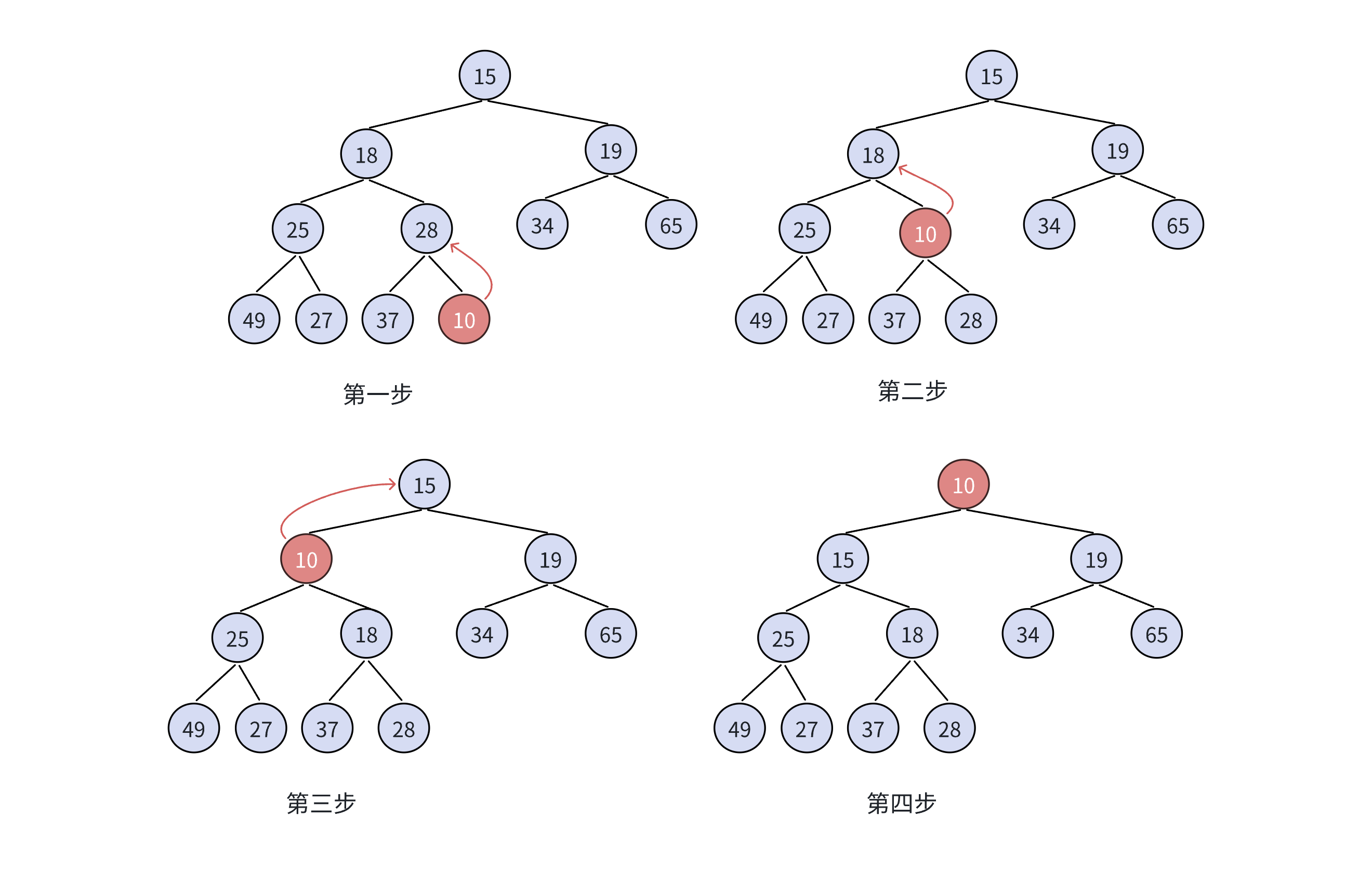












)




)



